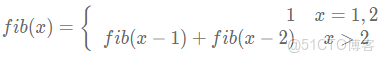1.題目

描述

大家都知道斐波那契數列，現在要求輸入一個正整數 n ，請你輸出斐波那契數列的第 n 項。

斐波那契數列是一個滿足：

數據範圍：1≤n≤40

要求：空間複雜度 O(1)，時間複雜度 O(n) ，本題也有時間複雜度 O(logn)的解法

輸入描述：

一個正整數n

返回值描述：

輸出一個正整數。

示例1

輸入：

4

返回值：

3

説明：

根據斐波那契數列的定義可知，fib(1)=1,fib(2)=1,fib(3)=fib(3-1)+fib(3-2)=2,fib(4)=fib(4-1)+fib(4-2)=3，所以答案為3。

示例2

輸入：

1

返回值：

1

示例3

輸入：

2

返回值：

1

2. 題解思路

其實題目已經給出了斐波那契數列的規律，我們只需要按照模板解題就可以。

具體解題思路是：

如果文字描述的不太清楚，你可以參考視頻的詳細講解：B站@好易學數據結構

3.編碼實現

核心代碼如下：

func Fibonacci(n int) int {
    if n <= 2 {
        return 1
    }
    // 1. 定義狀態. i:第i個斐波那契數； dp[i]:第i個斐波那契數值
    dp := make([]int, n+1)
    // 2. 初始化邊界條件
    dp[1] = 1
    dp[2] = 1
    // 3. 確定遞推公式
    for i := 3; i <= n; i++ {
        dp[i] = dp[i-1] + dp[i-2]
    }
    //4.輸出結果
    return dp[n]
}

具體完整代碼你可以參考下面視頻的詳細講解。

• Python編碼：B站@好易學數據結構
• Java編碼：B站@好易學數據結構
• Golang編碼：B站@好易學數據結構

4.總結

由於本題給出了斐波那契數列的遞推公式（數學表達式），因此只需要套用模板寫出代碼即可。本題的重點在於模板如何如何應用到動態規劃的題目中。

《數據結構與算法》深度精講課程正式上線啦！7大核心算法模塊全解析：

  ✅   鏈表

  ✅   二叉樹

  ✅   二分查找、排序

  ✅   堆、棧、隊列

  ✅   回溯算法

  ✅   哈希算法

  ✅   動態規劃

無論你是備戰筆試面試、提升代碼效率，還是突破技術瓶頸，這套課程都將為你構建紮實的算法思維底座。🔥立即加入學習打卡，與千名開發者共同進階！

• Python編碼實現：B站@好易學數據結構
• Java編碼實現：B站@好易學數據結構
• Golang編碼實現：B站@好易學數據結構

對於LeetCode數據結構與算法，我們總結了一套【可視化+圖解】方法，依據此方法來解決相關問題，算法變得易於理解，寫出來的代碼可讀性高也不容易出錯。具體也可以參考視頻詳細講解。

今日佳句：萬物各得其和以生，各得其養以成。