卡爾曼濾波是什麼
卡爾曼濾波適用於估計一個動態系統的最優狀態。即便是觀測到的系統狀態參數含有噪聲,觀測值不準確,卡爾曼濾波也能夠完成對狀態真實值的最優估計。網上大多數的教程講到卡爾曼的數學公式推導,會讓人很頭疼,難以把握其中的主線和思想。所以我參考了國外一位學者的文章,講述卡爾曼濾波的工作原理,然後編寫了一個基於OpenCV的小程序給大家做一下説明。下面的這個視頻請大家先直觀地看看熱鬧吧~
角度跟蹤視頻
卡爾曼濾波能做什麼
假設我們手頭有一輛DIY的移動小車。這輛車的外形是這樣的:
這輛車可以在荒野移動,為了便於對它進行控制,需要知道它的位置以及移動速度。所以,建立一個向量,用來存儲小車的位置和速度 :
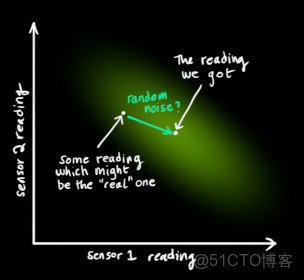
其實,一個系統的狀態有很多,選擇最關心的狀態來建立這個狀態向量是很重要的。例如,狀態還有水庫裏面水位的高低、鍊鋼廠高爐內的温度、平板電腦上面指尖觸碰屏幕的位置等等這些需要持續跟蹤的物理量。好了,迴歸到正題,小車上面安裝了GPS傳感器,這個傳感器的精度是10米。但是如果小車行駛的荒野上面有河流和懸崖的話,10米的範圍就太大,很容易掉進去進而無法繼續工作。所以,單純靠GPS的定位是無法滿足需求的。另外,如果有人説小車本身接收操控着發送的運動指令,根據車輪所轉動過的圈數時能夠知道它走了多遠,但是方向未知,並且在路上小車打滑車輪空轉的現象絕對是不可避免。所以,GPS以及車輪上面電機的碼盤等傳感器是間接地為我們提供了小車的信息,這些信息包含了很多的和不確定性。如果將所有這些信息綜合起來,是否能夠通過計算得到我們更想要的準確信息呢?答案是可以的!我們不希望小車在荒野當中這樣:
卡爾曼濾波的工作原理
卡爾曼濾波的工作原理主要包括先驗估計和後驗估計。什麼意思,請看下文:
1.先驗狀態估計
為了簡化我們的例子,假如小車在一條絕對筆直的線路上面行駛,其運動軌跡是確定的,不確定的是小車的速度大小和位置。於是,套路來了:
狀態變量:
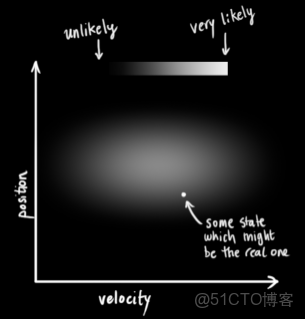
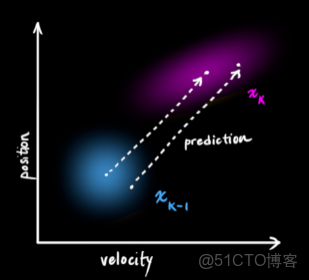
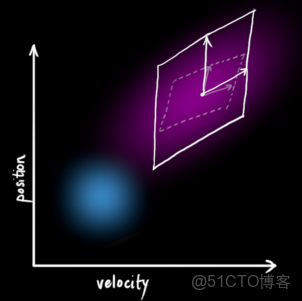
更直觀地,下圖表示的是一個狀態空間,橫座標是速度,縱座標是位置,平面上面的任意一個點就唯一地描述出這個小車的運動狀態。
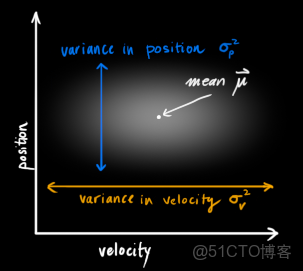
卡爾曼濾波器發生作用的前提是小車的速度和位置量在其定義域內具有正態的高斯分佈規律。用數學語言來講,就是每一個變量都是具有一個平均值
(這個值在變量的概率密度函數分佈圖的最中心位置,代表該數值是最可能發生的)和
(這個數值代表方差,表示變量的不確定性程度)。那麼,一談到概率統計,我們馬上可以想到:相互獨立,或者互不相關。即已知其中一個變量的變換規律,我們無法推斷出另外一個變量的變化規律。就像下圖所示的這樣(越亮的區域,表示發生的可能性越高):
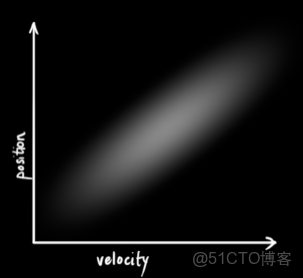
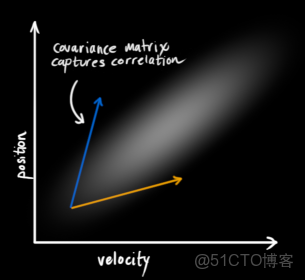
但是,相互獨立的反面就是相關。下圖所示的規律一看就明白,速度越大,位移也越大,這種情況下,兩個變量相關(其實這種情況是很有可能發生的,因為速度越大的話,可能小車就遠離我們,速度越小,表明靠近我們)。那麼,通過協方差矩陣\Sigma 就能夠將幾個變量的相關程度描述清楚。矩陣當中的某一個元素
表示的是狀態向量的第
個元素和第
個元素之間的相關程度,
。
要注意的是協方差矩陣是一個對稱陣。感興趣的童鞋可以深入研究一下,協方差矩陣的特徵值和特徵向量所具有的幾何意義:the directions in which the data varies the most.啥意思,就是哪個方向變化快,特徵向量指哪兒。
下面的兩個鏈接供大家參考,有興趣的要好好看看,知識點融會貫通了才覺得有意思!
協方差的特徵向量是什麼
協方差的幾何意義
下面是重頭戲:數學描述部分:
定義:
是狀態向量,
是協方差。 下圖描述了一個k-1時刻
和
時刻的狀態:我們其實是完全有理由根據前一時刻的狀態來預測下一時刻的狀態,這就是狀態更新方程。
於是,習慣性地要寫成矩陣的形式:
(1)
狀態向量的更新有了,但是還缺少狀態向量之間相關性的更新,也就是協方差矩陣。
結合(1)得到:
(先驗狀態估計向量)
(先驗狀態估計協方差矩陣)
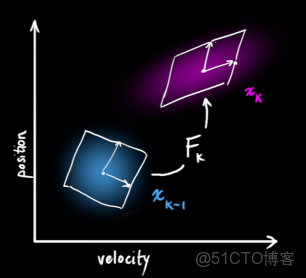
外部確定性影響
確定影響,比如:小車的操控者發出一條剎車的指令,我們通過建模該指令,假如小車的加速度為
,根據運動學的公式,得到:
寫成矩陣的形式就是:
其中,
是控制矩陣,
是控制向量。由於本例子當中的控制實際上只包含了加速度,所以該向量包含元素的個數為1。
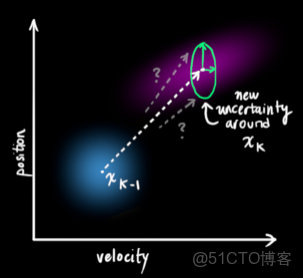
外部不確定性影響 現實世界往往是不那麼好描述清楚的,就是存在不確定的外部影響,會對系統產生不確定的干擾。我們是無法對這些干擾進行準確的跟蹤和量化的。所以,除了外界的確定項,還需要考慮不確定干擾項
。
從而,得到最終先驗估計的更新方程:
每一次的狀態更新,就是在原來的最優估計的基礎上面,下一次的狀態落在一個新的高斯分佈區域,從座標系上面看就像是一團雲狀的集合,最優的估計就在這個雲團當中的某一處。所以,我們首先要弄清楚這個雲團具有什麼樣的性質,也就是使用過程激勵噪聲協方差來描述不確定干擾。注意,
。
到此,先驗估計的過程結束,總結一下,形成如下的公式:
(2)
(3)重點來了:
先驗估計
取決於如下三部分:一部分是上一次的最優估計值(也就是上一輪卡爾曼濾波的結果),一部分是確定性的外界影響值,另一部分是環境當中不確定的干擾。先驗估計協方差矩陣
,首先是依據第
次卡爾曼估計(後驗估計)的協方差矩陣進行遞推,再與外界在這次更新中可能對系統造成的不確定的影響求和得到。
2.後驗估計(量測更新)
到此,利用
和
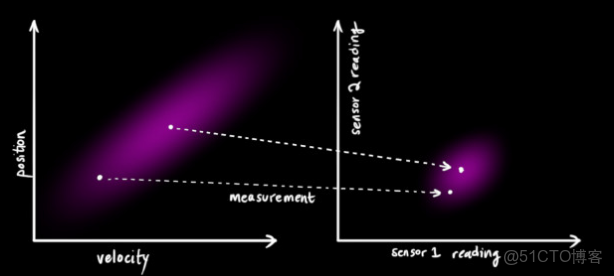
能夠對系統進行粗略的跟蹤,但是還不完善,因為人們總是不能夠完全信任自身的經驗,也需要另外的一條途徑來糾正潛在發生的錯誤或者是誤差。所以,我們很自然的想到在車身安裝各類的傳感器,比如速度傳感器、位移傳感器等等,以這些傳感器的反饋作為糾正我們推斷的依據。下面看看傳感器的量測更新是怎麼樣對最終的估計產生影響的。下圖説明的是狀態空間向觀測空間的映射。
在這裏需要説明一下,卡爾曼濾波器的觀測系統的維數小於等於動態系統的維數,即觀測量可以少於動態系統中狀態向量所包含的元素個數。
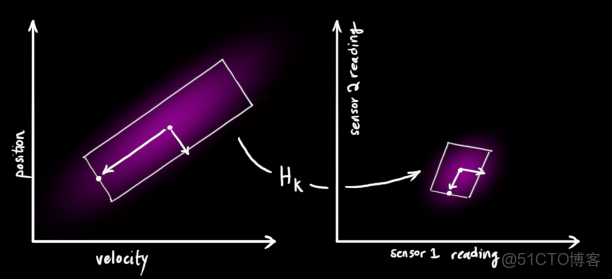
注意,傳感器的輸出值不一定就是我們創建的狀態向量當中的元素,有時候需要進行一下簡單的換算。即使是,有可能單位也不對應,所以,需要一個轉換。這個轉換就是矩陣
,在一些文獻當中也被稱作狀態空間到觀測空間的映射矩陣。
通過空間映射矩陣,依據我們先驗估計值,在量測空間當中,傳感器的測量值理想情況下應該是這樣的:
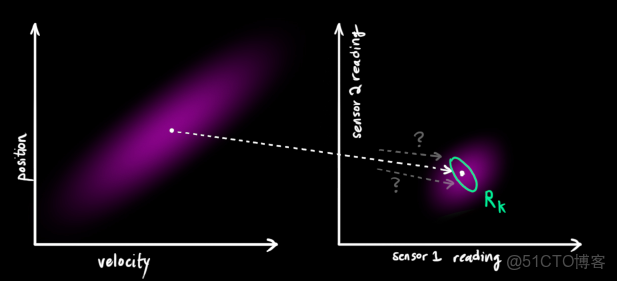
但是,傳感器對系統某些狀態的測量真的準確嗎?是不是也會有偏差呢?答案是肯定的。系統在某一個狀態下,會推斷出一組理想值,在另一個狀態下,會有另外一組理想值,而對應時刻傳感器的測量值一定是無法和理想值保持完全吻合的。由於測量噪聲的存在,不同的系統狀態下,測量具有一定誤差,呈現高斯分佈,但是這個高斯分佈的最中心還是當前的測量值。所以,還需要一個觀測噪聲向量以及觀測噪聲協方差來衡量測量水平,我們將它們分別命名為和。下面的兩張圖説明這一點。
觀測向量
服從高斯分佈,並且其平均值認為就是本次的量測值
。
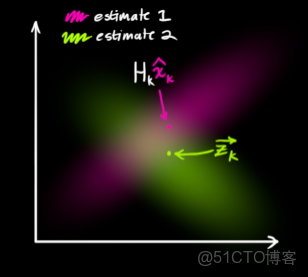
下圖看到的是兩個雲團,一個是狀態預測值,另一個是觀測值。那麼到底哪一個具體的結果才是最好的呢?現在需要做的是對這兩個結果進行合理的取捨(本質就是加權濾波),通過一種方法完成最終的卡爾曼預測。即:從圖中粉紅色雲團和綠色雲團當中找到一個最合適的點。
問題來了,怎麼找?
首先來直觀理解一下:考察觀測向量
和先驗估計
:存在兩個事件:事件1傳感器的輸出是對系統狀態真實值的完美測量,絲毫不差;事件2先驗狀態估計的結果就是系統狀態真實值的完美預測,也是絲毫不差。但是大家讀到這裏心裏非常清楚的一點是:兩個事件的發生都是概率性的,不能完全相信其中的任何一個!!!!!!!
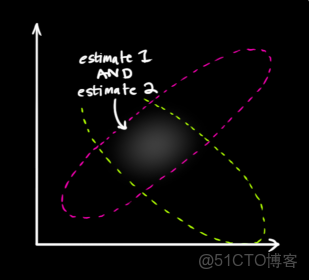
如果我們具有兩個事件,如果都發生的話,從直覺或者是理性思維上講,是不是認定兩個事件發生就找到了那個最理想的估計值?好了,抽象一下,得到:兩個事件同時發生的可能性越大,我們越相信它!要想考察它們同時發生的可能性,就是將兩個事件單獨發生的概率相乘。
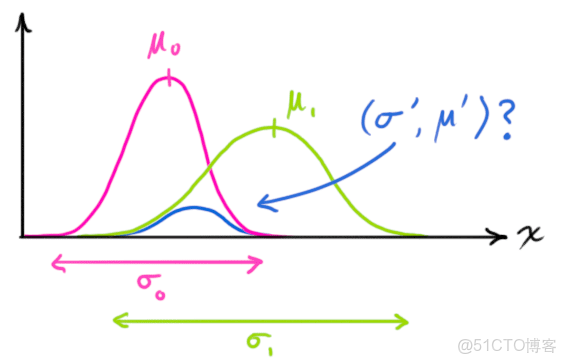
那麼,下一步就是對兩個雲團進行重疊,找到重疊最亮的點(實際上我們能夠把雲團看做一幀圖像,這幀圖像上面的每一個像素具有一個灰度值,灰度值大小代表的是該事件發生在這個點的概率密度),最亮的點,從直覺上面講,就是以上兩種預測準確的最大化可能性。也就是得到了最終的結果。非常神奇的事情是,對兩個高斯分佈進行乘法運算,得到新的概率分佈規律仍然符合高斯分佈,然後就取下圖當中藍色曲線峯值對應的橫座標不就是結果了嘛。證明如下:
我們考察單隨機變量的高斯分佈,期望為
,方差為
,概率密度函數為:
(4)
如果存在兩個這樣的高斯分佈,只不過期望和方差不同,當兩個分佈相乘,得到什麼結果?
是不是下式成立
(5)
將(4)代入(5),對照(4)的形式,求得:
其中,
以上是單變量概率密度函數的計算結果,如果是多變量的,那麼,就變成了協方差矩陣的形式:
卡爾曼增益,在下一步將會起到非常重要的作用。 好了,馬上就要接近真相!
卡爾曼估計
下面就是對傳感器的量測結果和根據
時刻預測得到的結果進行融合。(由於剛才的推導是兩個單變量,並且處在同一個空間內,下面的推導為了方便起見,我們將先驗狀態估計對應的結果映射到觀測向量空間進行統一的運算)
第一個要解決的問題是:(7)和(8)兩個式子中那個平均值和方差都對應多少?
將(9)和(10)代入(6)、(7)、(8)三個式子,整理得到:
其中卡爾曼增益為:
最後一步,更新結果:
其中,
就是第k次卡爾曼預測結果。
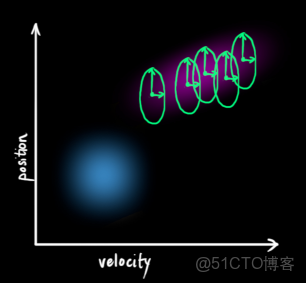
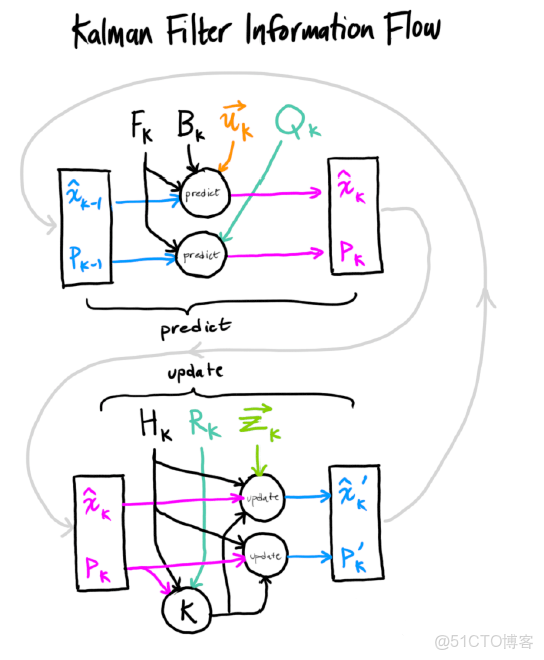
是該結果的協方差矩陣。它們都作為下一次先驗估計的初始值參與到新的預測當中。總體上來講,卡爾曼濾波的步驟大致分為兩步,第一步是時間更新,也叫作先驗估計,第二步是量測更新,也叫作後驗估計,而當前的卡爾曼濾波過程的後驗估計結果不僅可以作為本次的最終結果,還能夠作為下一次的先驗估計的初始值。下圖是卡爾曼濾波的工作流程:
對卡爾曼濾波原理的理解,我參考了這篇文章,圖片取自該文章,該文的圖片和公式顏色區分是一大亮點,在此表示對作者的感謝。
-----------------------------------------------------------------華麗的分割線:將上述理論進行總結-------------------------------------------------
1、先驗估計(兩個公式)
2、最終結果(三個公式)
其中,Hk為觀測空間的映射矩陣,Zk為觀測輸出(實際輸出),Zk - HkXk 即為 誤差e
----------------------------------------------------------------華麗的分割線:將上述理論進行總結-------------------------------------------------
舉個栗子
這部分重點講解一下利用OpenCV如何實現一個對三維空間內物體的二維平面跟蹤。
背景:跟蹤一個移動速度大小和方向大致保持不變的物體,檢測該物體的傳感器是通過對物體拍攝連續幀圖像,經過逐個像素的分析計算,得到x、y方向的速度,將兩個速度構成一個二維的列向量作為觀測向量。
下面看一下OpenCV當中對卡爾曼濾波的支持和提供的接口説明。
OpenCV2.4.13-KalmanFilter 下面是參與到卡爾曼濾波的一些數據結構,它們代表的意義在其後面用英文進行了描述。
OpenCV將以下的成員封裝在了KalmanFilter當中,我們使用時候,可以直接實例化一個對象,例如:
KalmanFilter m_KF;
//CV_PROP_RW Mat statePre; //!< predicted state (x'(k)): x(k)=A*x(k-1)+B*u(k)
//CV_PROP_RW Mat statePost; //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
//CV_PROP_RW Mat transitionMatrix; //!< state transition matrix (A)
//CV_PROP_RW Mat controlMatrix; //!< control matrix (B) (not used if there is no control)
//CV_PROP_RW Mat measurementMatrix; //!< measurement matrix (H)
//CV_PROP_RW Mat processNoiseCov; //!< process noise covariance matrix (Q)
//CV_PROP_RW Mat measurementNoiseCov;//!< measurement noise covariance matrix (R)
//CV_PROP_RW Mat errorCovPre; //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/
//CV_PROP_RW Mat gain; //!< Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
//CV_PROP_RW Mat errorCovPost; //!< posteriori error estimate covariance matrix (P(k)): P(k)=(I-K(k)*H)*P'(k)
KalmanFilter類的成員函數具有如下幾個:
KalmanFilter
init
predict
correct
方法很簡單,但是需要知道如何使用:
程序當中,我單獨寫了一個類,在我的計算線程(就是獲取到量測結果的線程)當中對該類進行實例化並且調用其中的方法。量測結果存放在
m_dispacementVector[0] = m_xSpeed;
m_dispacementVector[1] = m_ySpeed;
當中。
步驟一:
CV_WRAP KalmanFilter( int dynamParams, int measureParams, int controlParams = 0, int type = CV_32F );
/** @brief Re-initializes Kalman filter. The previous content is destroyed.
@param dynamParams Dimensionality of the state.
@param measureParams Dimensionality of the measurement.
@param controlParams Dimensionality of the control vector.
@param type Type of the created matrices that should be CV_32F or CV_64F.
*/
在卡爾曼濾波類的構造函數成員列表當中首先告知OpenCV過程狀態向量的維度和觀測向量的維度:
m_KF(4,2,0)1狀態向量初始化
我想對物體的位置信息和速度信息進行跟蹤,由於是二維的,所以位置信息x、y方向兩個變量,
速度信息x、y方向兩個變量,從而
m_KF.statePre
和
m_KF.statePost是一個四維列向量。
該向量在初始化時設置為零。 2狀態轉移矩陣初始化
在計算機屏幕上面,我自定義了一個該物體的運動空間,具有橫縱座標,後面會看到這個空間。
由於相機的幀率是30fps,所以相鄰幀時間間隔
,被測物體的實際速度大約為10mm/s,
所以在如此短的時間內,該物體能夠認為是做勻速直線運動,故得到狀態轉移方程
m_KF.transitionMatrix = (Mat_<float>(4, 4) << 1, 0, 0.03, 0,0,1,0,0.03,0,0,1,0,0,0,0,1);3過程噪聲激勵協方差矩陣
setIdentity(m_KF.processNoiseCov, Scalar::all(1e-5));//Q
認為過程激勵噪聲比較弱,並且每個分量相互之間不存在相關係。
4觀測矩陣
setIdentity(m_KF.measurementMatrix);
初始化得到:
由於傳感器只是檢測到了兩個方向的速度,對位移沒有檢測,所以要將矩陣前兩列初始化為0。
5預測估計協方差矩陣
setIdentity(m_KF.errorCovPost, Scalar::all(1));
初始化為單位陣。
6測量噪聲協方差矩陣
setIdentity(m_KF.measurementNoiseCov, Scalar::all(1e-1));//R
步驟二:
先驗估計
m_prediction = m_KF.predict();
步驟三:
後驗估計: 首先需要告知卡爾曼濾波器最新的傳感器數據:
m_dispacementVector[0] = m_xSpeed;
m_dispacementVector[1] = m_ySpeed;
m_pKalman->updateMeasurements(m_dispacementVector);
void kalmanFilter::updateMeasurements(double p[])
{
m_measurement = (Mat_<float>(2, 1) << p[0], p[1]);
}
接着完成後驗估計:
m_KF.correct(m_measurement);
KalmanFilter.h:
#include <QObject>
#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui/highgui.hpp"
using namespace cv;
class kalmanFilter:public QObject
{
Q_OBJECT
public:
kalmanFilter();
~kalmanFilter();
void initKalman();
void kalmanPredict();
void updateMeasurements(double p[]);
void kalmamCorrect();
double *returnResult();
void drawArrow(Point start, Point end, Scalar color, int alpha, int len);
private:
KalmanFilter m_KF;
Mat m_state;
Mat m_postCorrectionState;
Mat m_processNoise;
Mat m_measurement;
Mat m_img;
Mat m_prediction;
Point2f m_PointCenter;
};
KalmanFilter.cpp:
#include "kalmanFilter.h"
#include <iostream>
#include <fstream>
//CV_PROP_RW Mat statePre; //!< predicted state (x'(k)): x(k)=A*x(k-1)+B*u(k)
//CV_PROP_RW Mat statePost; //!< corrected state (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
//CV_PROP_RW Mat transitionMatrix; //!< state transition matrix (A)
//CV_PROP_RW Mat controlMatrix; //!< control matrix (B) (not used if there is no control)
//CV_PROP_RW Mat measurementMatrix; //!< measurement matrix (H)
//CV_PROP_RW Mat processNoiseCov; //!< process noise covariance matrix (Q)
//CV_PROP_RW Mat measurementNoiseCov;//!< measurement noise covariance matrix (R)
//CV_PROP_RW Mat errorCovPre; //!< priori error estimate covariance matrix (P'(k)): P'(k)=A*P(k-1)*At + Q)*/
//CV_PROP_RW Mat gain; //!< Kalman gain matrix (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
//CV_PROP_RW Mat errorCovPost; //!< posteriori error estimate covariance matrix (P(k)): P(k)=(I-K(k)*H)*P'(k)
using namespace cv;
using namespace std;
kalmanFilter::kalmanFilter()
:m_KF(4,2,0)
, m_state(4,1,CV_32F)
, m_processNoise(4, 1, CV_32F)
, m_measurement(2,1,CV_32F)
, m_img(300, 300, CV_8UC3)
, m_PointCenter(m_img.cols*0.5f, m_img.rows)
{
m_KF.transitionMatrix = (Mat_<float>(4, 4) << 1, 0, 0.03, 0,0,1,0,0.03,0,0,1,0,0,0,0,1);//A
setIdentity(m_KF.measurementMatrix);
setIdentity(m_KF.processNoiseCov, Scalar::all(1e-5));//Q
setIdentity(m_KF.measurementNoiseCov, Scalar::all(1e-1));//R
setIdentity(m_KF.errorCovPost, Scalar::all(1));
}
kalmanFilter::~kalmanFilter()
{
}
void kalmanFilter::initKalman()
{
m_state = (Mat_<float>(4, 1) << 0,0,0,0);
m_KF.statePre = (Mat_<float>(4, 1) << m_PointCenter.x, m_PointCenter.y, 0, 0);
m_KF.statePost = (Mat_<float>(4, 1) << m_PointCenter.x, m_PointCenter.y, 0, 0);
m_KF.measurementMatrix = (Mat_<float>(2, 4) << 0,0, 1, 0,0,0,0,1);
}
void kalmanFilter::updateMeasurements(double p[])
{
m_measurement = (Mat_<float>(2, 1) << p[0], p[1]);
}
void kalmanFilter::kalmanPredict()
{
m_prediction = m_KF.predict();
}
void kalmanFilter::kalmamCorrect()
{
m_KF.correct(m_measurement);
m_postCorrectionState = m_KF.statePost;
//show the result
m_img = Scalar::all(0);
//measured result
drawArrow(Point(m_KF.statePost.at<float>(0, 0), m_KF.statePost.at<float>(1, 0)),
Point(m_KF.statePost.at<float>(0, 0) + m_measurement.at<float>(0, 0), m_KF.statePost.at<float>(1, 0) + m_measurement.at<float>(1, 0)),
Scalar(0, 0, 255), 20, 15);//B G R
putText(m_img, "measurement", Point(m_KF.statePost.at<float>(0, 0) + m_measurement.at<float>(0, 0), m_KF.statePost.at<float>(1, 0) + m_measurement.at<float>(1, 0)-5), FONT_HERSHEY_PLAIN, 1, Scalar(0, 0, 255), 2);
//predicted result
drawArrow(Point(m_KF.statePost.at<float>(0, 0), m_KF.statePost.at<float>(1, 0)),
Point(m_KF.statePost.at<float>(0, 0) + m_KF.statePost.at<float>(2, 0), m_KF.statePost.at<float>(1, 0) + m_KF.statePost.at<float>(3, 0)),
Scalar(0,255, 0), 20, 15);
putText(m_img, "Kalman", Point(m_KF.statePost.at<float>(0, 0) + m_KF.statePost.at<float>(2, 0)-10, m_KF.statePost.at<float>(1, 0) + m_KF.statePost.at<float>(3, 0)-5), FONT_HERSHEY_PLAIN, 1, Scalar(0, 255, 0), 2);
imshow("Kalman", m_img);
ofstream myfile("example.txt", ios::app);
myfile << "measure" << " "<<m_measurement.at<float>(0, 0) << " " << m_measurement.at<float>(1, 0)<<" ";
myfile << "kalman" << " " << m_KF.statePost.at<float>(2, 0) << " " << m_KF.statePost.at<float>(3, 0) << endl;
}
double * kalmanFilter::returnResult()
{
double result[4];
for (int i = 0; i < 4; i++)
{
result[i] = m_postCorrectionState.at<double>(i, 1);
}
return result;
}
void kalmanFilter::drawArrow(Point start, Point end, Scalar color,int alpha,int len)
{
const double PI = 3.1415926;
Point arrow;
double angle = atan2((double)(start.y - end.y), (double)(start.x - end.x));
line(m_img, start, end, color,2);
arrow.x = end.x + len * cos(angle + PI * alpha / 180);
arrow.y = end.y + len * sin(angle + PI * alpha / 180);
line(m_img, end, arrow, color,1);
arrow.x = end.x + len * cos(angle - PI * alpha / 180);
arrow.y = end.y + len * sin(angle - PI * alpha / 180);
line(m_img, end, arrow, color,1);
}
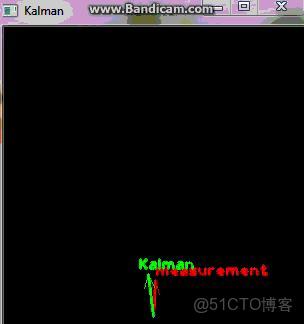
下面是錄製的程序運行效果圖(抱歉物體未顯示):
參考資料:
卡爾曼濾波器OpenCV自帶例子教程卡爾曼濾波的直覺理解