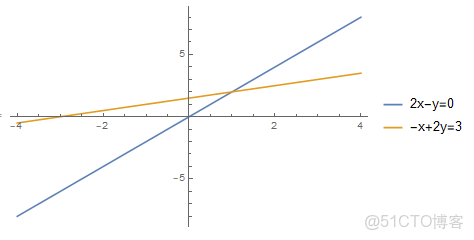本篇為MIT公開課——線性代數 筆記。
本篇為MIT公開課——線性代數 筆記。
二維舉例
兩未知數兩方程：
\[2 x-y=0\\ -x+2 y=3 \]
方程組的矩陣形式：
\[\left( \begin{array}{cc} 2 & -1 \\ -1 & 2 \\ \end{array} \right) \left( \begin{array}{c} x \\ y \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right) \]
這裏矩陣有兩行兩列，左手邊包括係數矩陣\(A\)，未知數向量 \(X\)，右側 向量\(b\)。
於是線性方程組可以寫成 \(A X =b\).
行圖像
一次取一行方程，作圖於 \(xy\)
做出滿足兩個方程的所有的點的圖像。
它們相交於點 \((1,2)\)。這個交點也是方程的解。
列圖像
我們重新看兩個方程
\[2 x-y=0\\ -x + 2 y=3 \]
兩個方程一起考慮，豎着看方程， \(x\) 和 \(y\)
\[x \left( \begin{array}{c} 2 \\ -1 \\ \end{array} \right)+y \left( \begin{array}{c} -1 \\ 2 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right) \]
這個方程的目的是尋找如何將左側的兩個已知向量正確組合然後構成右側的向量。即：\(\left( \begin{array}{c} 2 \\ -1 \\ \end{array} \right)\)和\(\left( \begin{array}{c} -1 \\ 2 \\ \end{array} \right)\)分別乘以對應數值然後相加，來製造向量\(\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right)\)，這個過程就是列向量的線性組合。這兩個數值就是我們要求解的。
在行圖像中我們解出 \(x\) =1, \(y\)
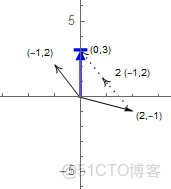
\[1 \left( \begin{array}{c} 2 \\ -1 \\ \end{array} \right)+2 \left( \begin{array}{c} -1 \\ 2 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right) \]
這個圖像是怎麼樣的呢？（向量的加法運算）
怎麼得來的？對於右側向量，第一個分量就是(從橫向看) \(1*2+2*(-1)=0\),第二個分量就是 \(1*(-1)+2*2=3\)
絕了。
那麼所有的線性組合又是什麼？
\[x \left(\begin{array}{c} 2 \\ -1 \\ \end{array} \right)+y \left( \begin{array}{c} -1 \\ 2 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 3 \\ \end{array} \right) \]
結果是我們可以得到所有可能的右側向量，它們會佈滿整個座標平面。也就是會得到一個面。
三維舉例
三未知數三方程：
\[\begin{align}2x-\,\,\,\,&y=0\\ -x+2&y-z=-1\\ -3&y+4z=4 \end{align} \]
係數矩陣和右側向量分別為：
\[\begin{align}&A=\left( \begin{array}{ccc} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -3 & 4 \\ \end{array} \right)\\ \\ &b=\left( \begin{array}{c} 0 \\ -1 \\ 4 \\ \end{array} \right) \end{align} \]
行圖像
三維圖像裏，每一行方程都是一個平面；在這個例子裏面，三個平面互不平行，所以兩個平面相交於一條直線，三個平面相交於一個點。
這個點就是我們的解。
但問題顯而易見：太難畫了！(不用軟件) 四維甚至更高維，問題更復雜，更加難畫。
此時列圖像將展現它的優勢。
列圖像
寫出列圖像矩陣形式：
\[x \left(\begin{array}{c} 2 \\ -1 \\ 0 \\ \end{array} \right)+y \left( \begin{array}{c} -1 \\ 2 \\ -3 \\ \end{array} \right)+z \left( \begin{array}{c} 0 \\ -1 \\ 4 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ -1 \\ 4 \\ \end{array} \right) \]
左側，我們要進行三個向量的線性組合，構造出右側向量。
可以看出，右側向量是左側向量其中一個，那麼結果很顯然：
\[x=0,y=0,z=1\]
正確的組合就是0個列1，0個列2，1個列3。
但這一道題是精心設計的，一般我們不會一眼看出結果。但可以看到他比行圖像簡單得多。
下一講講解矩陣消元法，來解方程組。
問題
對於該例子，考慮所有的右側向量，對任意 \(b\)
該例子中，係數矩陣 \(A\)
但對於某些情況，答案可能是否定的，比如三個列向量同處於一個平面，那麼它們的組合也一定在這個平面上，問題就出現了，因為 \(b\)
考慮九維
假設9未知數9方程，這樣就有9列，每一列都是9維空間的向量，考慮其線性組合 ，通過正確線性組合得到右側向量。
問題
同樣的，是否對於任意$ b$ 都能求解？
這還是取決於這9個向量，有時可以，有時不行。比如9列實際只有8列對結果有貢獻，這樣就會有一些 \(b\)
矩陣乘法
係數矩陣A乘以未知數向量等於右側向量，這是一種矩陣乘法運算。
\[A X =b\]
如何用矩陣乘以向量？
舉例，
\[\left(\begin{array}{cc} 2 & 5 \\ 1 & 3 \\ \end{array} \right) \left( \begin{array}{c} 1 \\ 2 \\ \end{array} \right) \]
兩種方法：
1.一次一列形式
取1個第一列和2個第二列
\[1 \left(\begin{array}{c} 2 \\ 1 \\ \end{array} \right)+2 \left( \begin{array}{c} 5 \\ 3 \\ \end{array} \right)=\left( \begin{array}{c} 12 \\ 7 \\ \end{array} \right) \]
向量的第一個分量乘以矩陣第一列，第二個分量乘以矩陣第二列，然後相加。
2.一次一行形式
矩陣第一行與向量點積得到右側向量第一個分量，第二行與向量點積得到右側向量的第二個分量。
\[(2,5)*(1,2)=12\\(1,3)*(1,2)=7\]
