樹模型
樹模型在機器學習中至關重要,它不僅本身具有較好的性能,也可以用於優化其他的算法。
我們在本節將要介紹優化
一、 的數據結構
的數據結構
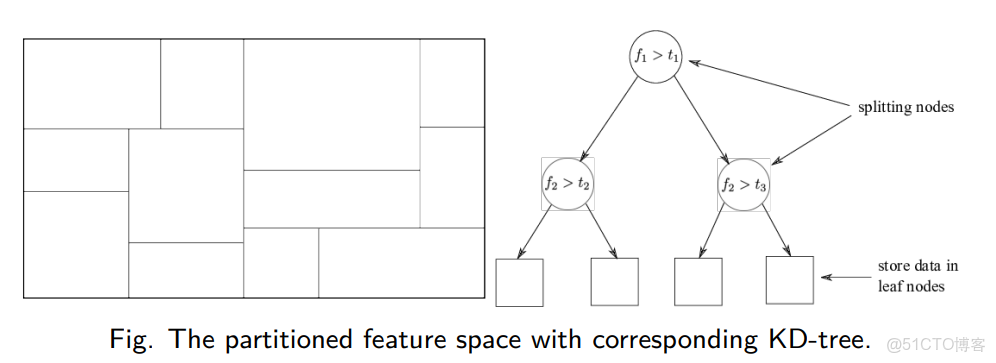
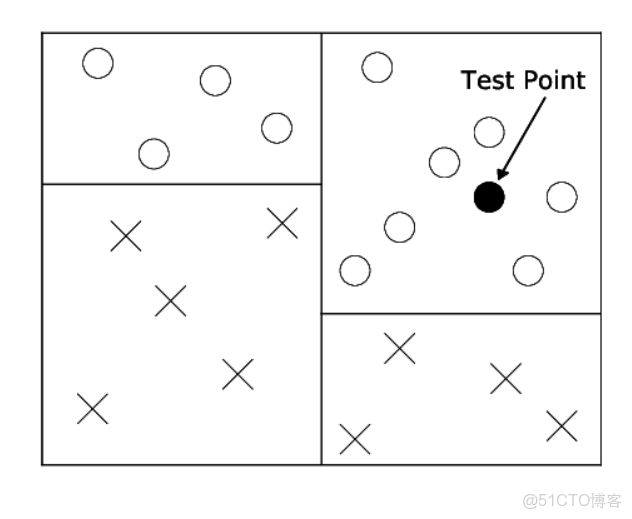
在KNN算法中我們要找到測試點的最近的K個鄰居,但是這需要我們求解所有點與測試點之間的距離(我們稱這個過程為線性掃描),在數據集很大時這顯然是不合理的,為此我們需要在此討論以下KNN算法的數據結構。
1.1 時間複雜度
我們首先回顧一下



顯然,隨着數據集的增大,計算量將變得巨大,導致算法運行速度很慢,這並不是我們想看到的
我們希望找到一個較好的數據結構,使得對測試點進行分類時不再需要遍歷每一個點。
1.2  樹
樹



構造



1.2.1 構造KD樹
構造
① 構造根節點,根節點對應特徵空間中包含所有實例點的超矩形區域。
② 在超矩形區域選擇一個座標軸和在此座標軸上的一個切分點,由此確定一個超平面,這個超平面通過選定的切分點並垂直於選定的座標軸,將當前的超矩形區域分為左右兩個子區域,這時該超矩形內的實例被分到了兩個子區域,生成兩個子節點。
③ 對每個結點重複執行②操作直到子區域內不再存在實例,由此得到的結點為葉子結點。
構造
輸入:

其中我們將特徵向量對應的數據集記為:

其中的特徵向量為

(1)開始:構造根節點:根節點對應包含

選擇


切分由通過切分點並與座標軸

將落在切分超平面上的實例點保存為根節點。
(2)重複:對深度為




由該節點生成深度為

將落在切分超平面上的實例點保存在該節點。
對於維度的選擇還有另一個方法,即選擇方差最大的維度去進行劃分,這樣可能會劃分得更好。
(3)直到兩個子區域沒有實例存在時停止,從而形成
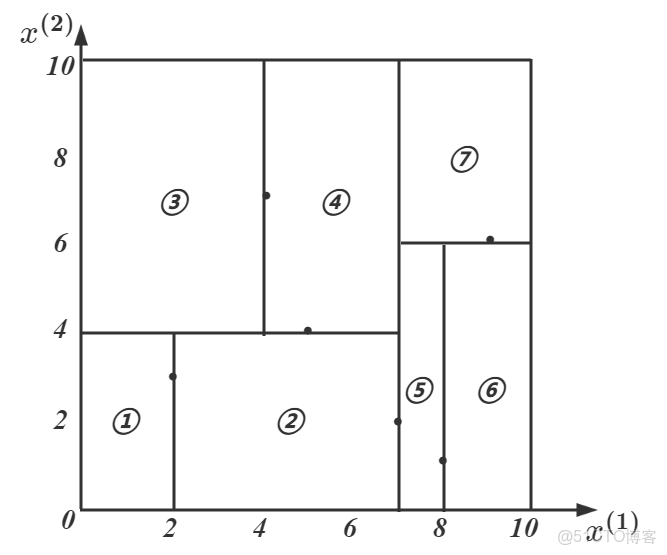
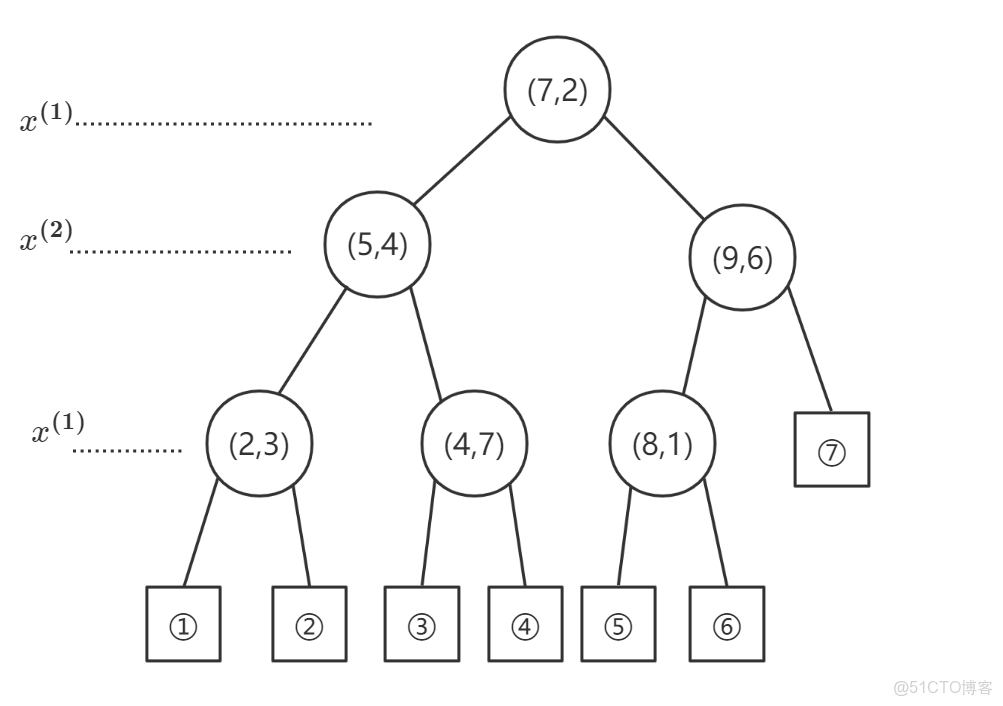
我們不妨在


其構造過程如下:
①選擇根節點:



左子區域包含:

②對深度為


左子區域切分點:

③對深度為


由此得到三個新的切分點:
由此得到的劃分如下圖所示:
得到的
注意:我們在實際的算法中往往並不會使用全部的實例點去構造
1.2.2 搜索KD樹
我們構造KD樹的目的還是用於進行分類,因此我們需要思考如何搜索KD樹來進行分類,k-近鄰的搜索方式如下:
①對於給定的測試點

②從該結點出發,依次退回到父節點,不斷查找與目標點最鄰近的結點
③當確定不可能存在更近的結點時中止,這樣搜索區域便被限制在空間的局部區域上了
為了更加直觀得理解該算法,我們進行詳細的分析:以
輸入:已構造的

輸出:
(1)在


(2)此葉子結點為“當前最近結點”,遞歸得向上回退,對每個結點進行如下操作:
① 如果該結點保存的實例點比“當前最近結點”離目標點
② 當前最近點一定存在於該結點的一個子結點對應的區域,檢查該子結點對應的父結點的另一子結點對應的區域中是否存在更近的點。
具體地,檢查另一子結點對應地區域是否與以目標點為球心、以目標點與當前最近結點的距離為半徑的超球體相交,如果相交則可能存在另一個子結點對應的區域內存在距離目標點更近的點,移動到另一個子結點,接着遞歸得進行搜索。
如果不相交則向上回退。
(3)當回退到根節點時,搜索結束。最後的“當前最近結點”記為
如果實例點是隨機分佈的,則





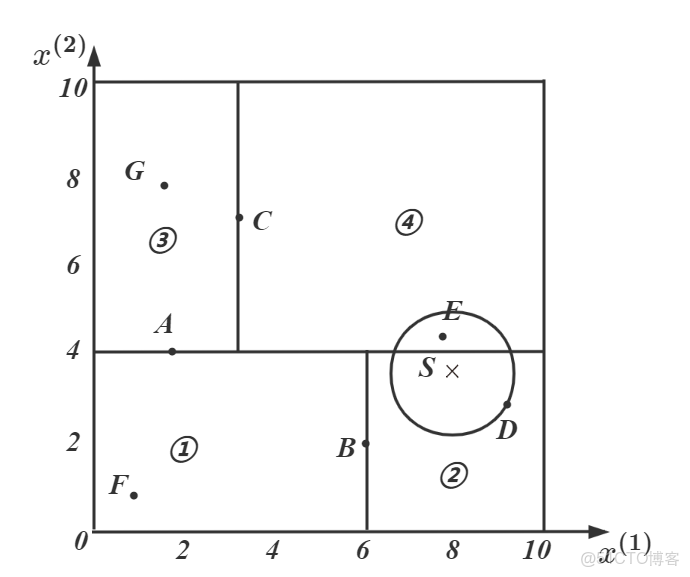
我們以下圖為例:

得到的
(1) 首先,我們找到了

(2) 然後,檢查葉子節點②的父節點
(3) 繼續,返回父節點
對應的區域中④與超球體相交,對④進行搜索找到了更近的點

(4) 最終,我們得到了
1.2.3 代碼實現
手動實現的代碼更加靈活,但鑑於筆者才疏學淺,我的選擇往往是調庫,手動實現是為了加強理解。
'''定義樹節點'''
class TreeNode:
def __init__(self,x=None,y=None,dim=None,left=None,right=None,father=None):
'''
:param x: 該結點存儲的特徵向量
'''
self.vec = x #特徵向量
self.label = y #樣本標籤
self.dim = dim #特徵維度
self.left = left #左子節點
self.right = right #右子節點
self.father = father #父節點接着我們定義用於構造和搜索Kd樹的類:
'''定義KD樹'''
class Kd_Tree(object):
'''初始化'''
def __init__(self,data,target):
self.n=len(data) #樣本數量
self.d=len(data[0]) #特徵維度數
self.X=data #存儲特徵向量數據集
self.Y=target #存儲標籤數據集
self.root=self.buildKdTree(data,target) #構造Kd樹
'''構造Kd樹'''
def buildKdTree(self,data,target,father=None):
'''
:param data: numpy數組,特徵向量
:param target: numpy數組,標籤向量
:return: Kd樹
'''
dataNum=len(data) #樣本數量
'''樣本為空,返回空'''
if dataNum==0:
return None
'''選擇切分的維度'''
varList=self.getVar(data)
maxVarDimIndex = varList.index(max(varList)) #找到方差最大的維度
sortIndex=data[:,maxVarDimIndex].argsort() #按照維度maxVarDimIndex從小到大排列的索引
'''找到中位數下標'''
mid=sortIndex[dataNum//2]
'''構造根節點'''
root=TreeNode(x=data[mid],y=target[mid],dim=maxVarDimIndex,father=father)
'''只有一個數據點時直接返回'''
if dataNum==1:
return root
'''劃分左右子樹並遞歸構造'''
leftdata=data[sortIndex[:dataNum//2]]
lefttatget=target[sortIndex[:dataNum//2]]
rightdata=data[sortIndex[dataNum//2+1:]]
righttarget=target[sortIndex[dataNum//2+1:]]
root.left=self.buildKdTree(leftdata,lefttatget,root)
root.right=self.buildKdTree(rightdata,righttarget,root)
return root
'''找到包含目標點的葉子節點'''
def findLeafNode(self,x,root):
if root==None: #樹為空
return None
if root.left==None and root.right==None: #樹只有一個結點
return root
node=root
while True: #找到葉子節點為止
dim=node.dim
if x[dim]<node.vec[dim]: #轉到左子結點
if not node.left: #左子節點為空
return node
node=node.left
else: #轉到右子節點
if not node.right: #右子節點為空
return node
node=node.right
'''搜索Kd樹'''
def searchKdTree(self,x,k):
'''
:param x: 目標點的特徵向量
:param k: k近鄰的參數k
:return: 分類標籤
'''
if self.n<=k: #所有的數據點都是近鄰
'''找到出現次數最多的標籤'''
labelNum={}
for label in self.Y:
if label not in labelNum.keys():
labelNum[label]=1
else:
labelNum[label]+=1
list=sorted(labelNum.items(),key=lambda x:x[1],reverse=True)
return list[0][0]
'''找到目標點x所屬的葉子節點'''
node=self.findLeafNode(x,self.root)
if node==None: #空樹情況
return None
'''計算葉子節點與目標點之間的歐式距離'''
eulerDistance=np.sqrt(sum((x-node.vec)**2)) #這是當前超球體半徑
nodeList=[] #存儲當前搜索到的k近鄰
nodeList.append([eulerDistance,tuple(node.vec),node.label]) #[距離distance,特徵向量vec,標籤label]
'''向上遞歸搜索'''
while True:
if node==self.root: #回溯到根節點,停止回溯
break
'''檢查父節點'''
father=node.father
fatherDistance=np.sqrt(sum((x-father.vec)**2))
'''
找到的近鄰小於k個或者當前超球體半徑與父節點對應的區域相交,則更新超球體半徑
'''
if k>len(nodeList) or eulerDistance>fatherDistance:
nodeList.append([fatherDistance,tuple(father.vec),father.label])
nodeList.sort() #從小到大排序
eulerDistance= nodeList[-1][0] if k > len(nodeList) else nodeList[k-1][0] #更新超球體半徑
'''找到的近鄰仍小於k個或者目標點到切分超平面的距離小於超球體半徑,即超球體與父節點的另一結點區域相交'''
if k>len(nodeList) or abs(x[father.dim]-father.vec[father.dim])<eulerDistance:
if x[father.dim]<father.vec[father.dim]: #目標點在父節點的左側區域,則要檢查右側區域
otherChild=father.right
nodeList=self.search(nodeList,otherChild,x,k) #檢查左側區域對超球體進行更新
else: #目標點在父節點的右側區域,則要檢查左側區域
otherChild=father.left
nodeList=self.search(nodeList,otherChild,x,k) #檢查右側區域對超球體進行更新
node=node.father #回溯到父節點
'''完成回溯,根據k近鄰進行統計'''
nodeList = nodeList[:k] if k <= len(nodeList) else nodeList
labelNum={}
for node in nodeList:
if node[2] not in labelNum:
labelNum[node[2]]=0
else:
labelNum[node[2]]+=1
list=sorted(labelNum.items(),key=lambda x:x[1],reverse=True)
return list[0][0]
'''輔助搜索函數:搜索另一子結點區域'''
def search(self,nodeList,root,x,k):
'''
與 searchKdTree 幾乎相同,只是減少了類別的統計與判斷
對以另一子結點為根的子樹進行搜索
'''
if root==None:
return nodeList
nodeList.sort()
dis = nodeList[-1][0] if k > len(nodeList) else nodeList[k-1][0] #當前超球體半徑
node=self.findLeafNode(x,root) #找到目標點在另一結點區域中的最近點
distance = np.sqrt(sum((x - node.vec)**2))
'''更細超球體半徑'''
if k>len(nodeList) or distance<dis:
nodeList.append([distance,tuple(node.vec),node.label])
nodeList.sort()
dis = nodeList[-1][0] if k > len(nodeList) else nodeList[k - 1][0]
'''向上遞歸搜索'''
while True:
if node==root:
break
'''檢查父節點'''
father=node.father
fatherDistance=np.sqrt(sum((x-father.vec)**2))
'''
找到的近鄰小於k個或者當前超球體半徑與父節點對應的區域相交,則更新超球體半徑
'''
if k>len(nodeList) or dis>fatherDistance:
nodeList.append([fatherDistance,tuple(father.vec),father.label])
nodeList.sort() #從小到大排序
dis= nodeList[-1][0] if k > len(nodeList) else nodeList[k-1][0] #更新超球體半徑
'''找到的近鄰仍小於k個或者目標點到切分超平面的距離小於超球體半徑,即超球體與父節點的另一結點區域相交'''
if k>len(nodeList) or abs(x[father.dim]-father.vec[father.dim])<dis:
if x[father.dim]<father.vec[father.dim]: #目標點在父節點的左側區域,則要檢查右側區域
otherChild=father.right
nodeList=self.search(nodeList,otherChild,x,k) #檢查左側區域對超球體進行更新
else: #目標點在父節點的右側區域,則要檢查左側區域
otherChild=father.left
nodeList=self.search(nodeList,otherChild,x,k) #檢查右側區域對超球體進行更新
node=node.father #回溯到父節點
return nodeList
'''計算各維度方差'''
def getVar(self,data):
return list(np.var(data,axis=0))由此我們可以定義以

'''定義KNN分類器'''
class KnnClassifier(object):
'''初始化k參數'''
def __init__(self,k):
self.k=k
'''構造Kd樹'''
def fit(self,data,target):
self.KdTree=Kd_Tree(data,target)
'''進行預測'''
def predict(self,X_test):
result=[]
for x_t in X_test:
result.append(self.KdTree.searchKdTree(x_t,self.k))
return np.array(result)注意,我們上述實現的代碼與我們的舉例存在不同,一方面我們選擇切分維度的方法是選擇方差最大的那個維度,另外我們搜索



我們可以用鳶尾花數據集對上述模型進行驗證:
'''使用鳶尾花數據集進行驗證'''
iris=load_iris()
data=iris.data
target=iris.target
'''數據集劃分'''
X_train,X_test,y_train,y_test=train_test_split(data,target,test_size=0.2,random_state=10)#選取20%的數據作為測試集
'''初始化模型'''
knn=KnnClassifier(3)
knn.fit(X_train,y_train)
y_pred=knn.predict(X_test)
print(accuracy_score(y_test,y_pred)) #0.9666666666666667可以發現正確率為0.967,模型效果良好,上述手動實現過程還是比較複雜的,在算法競賽過程中為了提高編碼效率,還是調庫效率較高,不過如果涉及到算法的優化的話,面向手動實現的代碼進行分析更有優勢。
1.2.4 總結
① KD樹是一種二叉樹,其中每個節點都是一個k維點。
② 可以將每個非葉節點視為隱式生成一個拆分超平面,該超平面將空間拆分為兩部分,稱為半空間。
③ 此超平面左側的點由該節點的左子樹表示,而超平面右側的點由右子樹表示。
④ 超平面方向的選擇方式如下:樹中的每個節點都與k維度中的一個維度相關聯,超平面垂直於該維度的軸。
1.3 球樹
球樹類似於KD樹,但是不用超平面對特徵空間進行分割,而是用超球面進行分割
ball結構允許我們沿着點所在的底層流形對數據進行分區,而不是重複剖析整個特徵空間(如KD樹)
1.3.1 偽碼實現
球樹的構造偽碼如下圖所示,因為其構造過程類似於
1.3.2 球樹應用
球樹的作用與


①
②

但是,拆分是軸對齊的,無法很好地延伸到更高的維度。
③ 球樹劃分了點所在的流形,而不是整個空間。這使得它在更高的維度上表現得更好。
二、決策樹
2.1 核心思想
假設我們進行一個二分類問題,如果我們知道一個測試點屬於一個100萬個點的集羣,所有這些點的標籤都為正值,那麼在我們計算測試點到這100萬個距離中的每一個點的距離之前,我們也會知道它的鄰居將為正值,由此就有了決策樹的思想。
決策樹的構建過程,我們不存儲訓練數據,而是使用訓練數據來構建一個樹結構,該結構遞歸地將空間劃分為具有類似標籤的區域。
決策樹特點:
① 首先,決策樹的根節點對應整個訓練集
② 然後,通過一個簡單的閾值

③ 
④ 選擇閾值

⑤ 理想情況下,所有的正節點都屬於一個子節點,所有的負節點都屬於另一個子節點。
⑥ 滿足上述條件後,則完成決策的構建,否則要繼續對葉子結點進行分割,直到所有葉子結點都屬於一個類或不再可分
決策樹在KNN之上的優點:
① 決策樹構建之後我們便不再需要存儲各個訓練數據,只需要存儲所有葉子結點的標籤
② 決策樹在測試期間速度非常快,因為測試輸入只需遍歷樹到一片葉子,預測是葉子的主要標籤
③ 決策樹不需要度量,因為分割基於特徵閾值而不是距離。
2.2 構造決策樹
我們所要構建的決策樹的目標是:
① 使得決策樹最大緊湊化
② 使得葉子結點都只包含一種標籤的結點
要找到一棵最小化的樹是一個NP完全問題,但是我們可以用貪婪策略非常有效地近似它。
我們不斷拆分數據,以最小化雜質函數,該函數用於測量子對象中的標籤純度。
我們首先了解一下構造決策樹用到的一些重要概念。
2.2.1 基尼係數
首先我們假設數據集

接着定義數據集的子集

然後我們可以定義輸入分數

基尼不純度:表示在樣本集合中一個隨機選中的樣本被分錯的概率,則整個數據集的基尼不純度為:

顯然當數據集

2.2.2 信息熵
信息是個很抽象的概念。人們常常説信息很多,或者信息較少,但卻很難説清楚信息到底有多少。比如一本五十萬字的中文書到底有多少信息量。直到1948年,香農提出了**“信息熵”**的概念,才解決了對信息的量化度量問題。信息熵這個詞是香農從熱力學中借用過來的。熱力學中的熱熵是表示分子狀態混亂程度的物理量。香農用信息熵的概念來描述信源的不確定度。信源的不確定性越大,信息熵也越大。
從機器學習的角度來看,信息熵表示的是信息量的期望值,我們的假設與雜質函數的假設相同,則信息量的定義如下:

由於信息熵是信息量的期望值,所以信息熵

同理我們可以定義決策樹的熵:

在實際的場景中,我們可能需要研究數據集中某個特徵等於某個值時的信息熵等於多少,這個時候就需要用到條件熵。條件熵



現在已經知道了什麼是熵,什麼是條件熵,接下來就可以看看什麼是信息增益了。
所謂的信息增益就是表示我已知條件X後能得到信息Y的不確定性的減少程度。
就好比,我在玩讀心術。你心裏想一件東西,我來猜。我已開始什麼都沒問你,我要猜的話,肯定是瞎猜。這個時候我的熵就非常高。然後我接下來我會去試着問你是非題,當我問了是非題之後,我就能減小猜測你心中想到的東西的範圍,這樣其實就是減小了我的熵。那麼我熵的減小程度就是我的信息增益。
所以信息增益如果套上機器學習的話就是,如果把特徵A對訓練集S的信息增益記為g(D, A)的話,那麼g(D, A)的計算公式就是:

我們不妨通過一個例子理解上述與熵相關的概念:我們有如下"客户流失數據集",0代表未流失,1代表流失
|
編號
|
性別
|
活躍度
|
是否流失
|
|
1
|
男
|
高
|
0
|
|
2
|
女
|
中
|
0
|
|
3
|
男
|
低
|
1
|
|
4
|
女
|
高
|
0
|
|
5
|
男
|
高
|
0
|
|
6
|
男
|
中
|
0
|
|
7
|
男
|
中
|
1
|
|
8
|
女
|
中
|
0
|
|
9
|
女
|
低
|
1
|
|
10
|
女
|
中
|
0
|
|
11
|
女
|
高
|
0
|
|
12
|
男
|
低
|
1
|
|
13
|
女
|
低
|
1
|
|
14
|
男
|
高
|
0
|
|
15
|
男
|
高
|
0
|
假如要算性別和活躍度這兩個特徵的信息增益的話,首先要先算總的信息熵和條件熵。
計算總的信息熵很簡單:15條數據中標籤為0的有10個,標籤為1的有5個

則可得總信息熵為:

接下來就是條件熵的計算,以性別為男的熵為例。表格中性別為男的數據有8條,這8條數據中有3條數據的標籤為1,有5條數據的標籤為0。所以根據條件熵的計算公式能夠得出該條件熵為:

同理,我們也可以計算出性別為女時的條件熵:

由此可得總的條件熵為:

接着我們可以按照相同的方法計算活躍度的條件熵:

由此可得性別和活躍度兩個特徵的信息增益:

那信息增益算出來之後有什麼意義呢?回到讀心術的問題,為了我能更加準確的猜出你心中所想,我肯定是問的問題越好就能猜得越準!換句話來説我肯定是要想出一個信息增益最大(減少不確定性程度最高)的問題來問你,顯然上述兩個特徵中活躍度的信息增益最高,而這也是
同時支持
信息增益一定非負,相關證明可以參考 如何證明信息增益一定大於0?
2.2.3  算法
算法
(1)中止條件:
①子集中的所有數據點具有相同的標籤

②沒有更多的特徵用於切分子集,比如兩個數據點的特徵向量相同但是標籤不同,停止拆分,並創建一個標籤為最常見標籤的葉子節點
(2)算法過程:
#假設數據集為D,標籤集為A,需要構造的決策樹為tree
def ID3(D, A):
if 'D中所有的標籤都相同':
return '標籤'
if '樣本中只有一個特徵或者所有樣本的特徵都一樣':
'對D中所有的標籤進行計數'
return '計數最高的標籤'
'計算所有特徵的信息增益'
'選出增益最大的特徵作為最佳特徵(best_feature)'
'將best_feature作為tree的根結點'
'得到best_feature在數據集中所有出現過的值的集合(value_set)'
for value in value_set:
'從D中篩選出best_feature=value的子數據集(sub_feature)'
'從A中篩選出best_feature=value的子標籤集(sub_label)'
#遞歸構造tree
tree[best_feature][value] = ID3(sub_feature, sub_label)
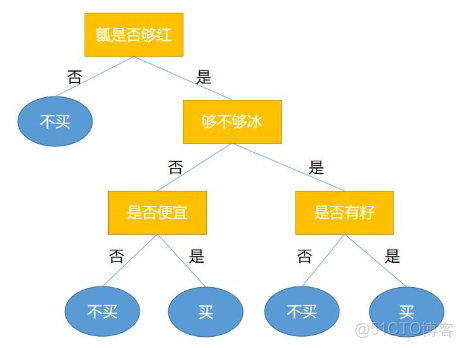
return tree比如我們辨別西瓜好壞的決策樹如下:
很明顯上述的
算法實現如下:首先我們用到的庫為:
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''導入重要的庫'''
import numpy as np
import pandas as pd
import copy
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score決策樹模型為:
'''定義決策樹模型'''
class DecisionTree(object):
def __init__(self,data,target):
'''初始化一個用於統計標籤數量的模板'''
self.dictLabel={}
for y in target:
if y not in self.dictLabel.keys():
self.dictLabel[y]=0
'''決策樹模型'''
self.tree=self.buildTree_ID3(data,target)
'''構造決策樹'''
def buildTree_ID3(self,data,target):
if self.is_same_label(target): #D中所有的標籤都相同
return target[0] #返回相同的標籤
if len(data)==1 or self.is_same_vector(data): #樣本中只有一個特徵或者所有樣本的特徵都一樣
return np.argmax(np.bincount(target)) #返回數量最多的標籤
'''計算所有特徵的信息增益'''
Gain=self.calcInfoGain(data,target)
'''選出增益最大的特徵'''
Gain.sort(key=lambda x:x[1]) #按照信息增益進行排序
best_feature=Gain[-1][0]
# print(Gain)
# print("best_feature:",best_feature)
# print("信息增益:",Gain[-1][1])
'''將best_feature作為根節點'''
tree={}
tree[best_feature]={}
'''得到best_feature的取值集合'''
value_set=[]
for v in data[:,best_feature]:
if v not in value_set:
value_set.append(v)
'''遞歸得構造樹'''
'''首先整合數據集'''
dataset=[] #整合特徵向量與標籤,便於得到子數據集
for i in range(len(data)):
dataset.append((data[i],target[i]))
for value in value_set:
subset=np.array(list(filter(lambda x:x[0][best_feature]==value,dataset))) #首先對dataset進行過濾
'''從D中篩選出best_feature=value的子數據集(sub_feature)'''
sub_feature=np.array(list(np.array(subset)[:,0]))
'''從A中篩選出best_feature=value的子標籤集(sub_label)'''
sub_label=np.array(list(np.array(subset)[:,1]))
#上述數據集不需要再刪去特徵A,因為特徵A在子樹的信息增益一定為0
tree[best_feature][value]=self.buildTree_ID3(sub_feature,sub_label)
return tree
'''計算信息增益'''
def calcInfoGain(self,data,target):
'''
:param data: 特徵向量集,numpy數組
:param target: 標籤集,numpy數組
:return: Gain,Gain[i]=(index,g(D,A)),index為特徵索引,g(D,A)為信息增益
'''
'''計算總信息熵HD'''
labelNum=copy.deepcopy(self.dictLabel)#統計各類標籤數量
for y in target:
labelNum[y]+=1
HD=0.0 #總信息熵
dataNum=len(data)
for y in labelNum.keys():
p=labelNum[y]/dataNum
if not p==0:
HD+=-p*np.log2(p) #規避log(0)的情況
'''計算各個特徵的條件熵'''
HDA=[] #存儲各個特徵的條件熵
for A in range(len(data[0])):
'''首先統計特徵A的取值數量'''
valueNum={}
'''
valueNum[v]=(num,labelNum)
(num,labelNum)為特徵A取值為v的數據信息
num表示特徵A取值為v的樣本數量
labelNum記錄了特徵A取值為v的樣本中各類標籤的數量
'''
for i in range(dataNum):
value=data[i][A]
label=target[i]
if value not in valueNum:
labelNum=copy.deepcopy(self.dictLabel)
labelNum[label]+=1
valueNum[value]=[1,labelNum]
else:
valueNum[value][0]+=1 #取值為value的數量+1
valueNum[value][1][label]+=1
'''統計結束,計算總條件熵'''
ConEntropy=0.0 #特徵A的條件熵
for v in valueNum.keys():
p_v=valueNum[v][0]/dataNum
InfoEntropy=0.0 #特徵A取值為v的信息熵
for y in valueNum[v][1].keys():
p=valueNum[v][1][y]/valueNum[v][0]
if not p==0:
InfoEntropy+=-p*np.log2(p)
ConEntropy+=p_v*InfoEntropy
HDA.append((A,ConEntropy))
'''信息熵與各個特徵的條件熵計算完畢,統計信息增益'''
Gain=[]
for i in range(len(HDA)):
A=HDA[i][0]
G=HD-HDA[i][1]
Gain.append((A,G))
return Gain
'''判斷數據集中標籤是否都相同'''
def is_same_label(self,target):
y=target[0]
for i in range(1,len(target)):
if not target[i]==y:
return False
return True
'''判斷數據集中向量是否都相同'''
def is_same_vector(self,data):
x=data[0]
for i in range(1,len(data)):
if not (data[i]==x).all():
return False
return True決策樹分類器為:
'''定義決策樹分類器'''
class Classifiter(object):
'''無重要參數'''
def __init__(self):
pass
'''訓練模型'''
def fit(self,data,target):
self.decisionTree=DecisionTree(data,target) #構造決策樹
'''模型預測'''
def predict(self,X_test):
result=[]
for x_t in X_test:
node=self.decisionTree.tree #node初始化為根節點
while isinstance(node,dict): #只要node不是葉子節點,那麼它一定是字典
feature=list(node.keys())[0] #當前決策樹分支特徵
node=node[feature][x_t[feature]]
result.append(node)
return np.array(result)驗證模型時,我們用到的數據集為西瓜好壞數據集:watermelon20.xlsx
'''驗證模型效果'''
'''加載數據'''
df=pd.read_excel("data/watermelon_data.xlsx",sheet_name="Sheet1",header=0,index_col=0)
target=np.array(df["好瓜"])
target=np.where(target=="是",1,0) #修正標籤
df.drop("好瓜",axis=1,inplace=True)
data=df.values
'''數據集劃分'''
X_train,X_test,y_train,y_test=train_test_split(data,target,test_size=0.2,random_state=99)#選取20%的數據作為測試集
'''初始化模型'''
classifiter=Classifiter()
'''模型訓練與預測'''
classifiter.fit(data,target) #鑑於數據集太小,我們用全部數據進行訓練
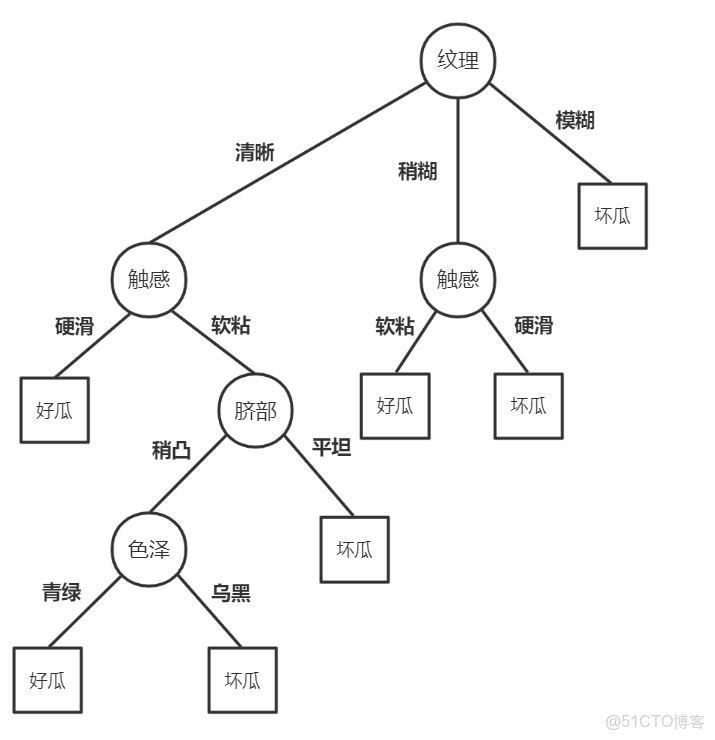
print(classifiter.decisionTree.tree) #決策樹
#{3: {'清晰': {5: {'硬滑': 1, '軟粘': {4: {'稍凹': {0: {'青綠': 1, '烏黑': 0}}, '平坦': 0}}}}, '稍糊': {5: {'軟粘': 1, '硬滑': 0}}, '模糊': 0}}
y_pred=classifiter.predict(X_test)
print(accuracy_score(y_test,y_pred)) #1.0最終我們得到的決策樹如下圖所示:
算法一個明顯的弊端是無法處理包含在訓練集中未出現過的特徵取值的測試點,這種情況經常出現在具有連續型特徵的數據集上,這要求我們的訓練集要足夠大,保證對各種取值的覆蓋,我們後面的
2.2.4  算法
算法





由於在使用信息增益這一指標進行劃分時,更喜歡可取值數量較多的特徵。為了減少這種偏好可能帶來的不利影響,Ross Quinlan使用了信息增益率這一指標來選擇最優劃分屬性,信息增益率的定義如下:
設數據集為





還記得我們剛剛舉的例子嗎,我們回到客户流失數據集中,可以很容易得計算信息增益率:

15條數據中8條是男性,7條是女性;4條低活躍度,5條中活躍度,6條高活躍度:

我們可以發現活躍度的信息增益率要比信息增益小很多,這就是
實現

calcInfoGain 函數:
'''計算信息增益率'''
def calcInfoGain(self,data,target):
'''
:param data: 特徵向量集,numpy數組
:param target: 標籤集,numpy數組
:return: Gain,Gain[i]=(index,g(D,A)),index為特徵索引,g(D,A)為信息增益
'''
'''計算總信息熵HD'''
labelNum=copy.deepcopy(self.dictLabel)#統計各類標籤數量
for y in target:
labelNum[y]+=1
HD=0.0 #總信息熵
dataNum=len(data)
for y in labelNum.keys():
p=labelNum[y]/dataNum
if not p==0:
HD+=-p*np.log2(p) #規避log(0)的情況
'''計算各個特徵的條件熵'''
HDA=[] #存儲各個特徵的條件熵
Ratio_base=[] #存儲計算信息增益率的底數
for A in range(len(data[0])):
'''首先統計特徵A的取值數量'''
valueNum={}
'''
valueNum[v]=(num,labelNum)
(num,labelNum)為特徵A取值為v的數據信息
num表示特徵A取值為v的樣本數量
labelNum記錄了特徵A取值為v的樣本中各類標籤的數量
'''
for i in range(dataNum):
value=data[i][A]
label=target[i]
if value not in valueNum:
labelNum=copy.deepcopy(self.dictLabel)
labelNum[label]+=1
valueNum[value]=[1,labelNum]
else:
valueNum[value][0]+=1 #取值為value的數量+1
valueNum[value][1][label]+=1
'''統計結束,計算總條件熵'''
ConEntropy=0.0 #特徵A的條件熵
base=0.0
for v in valueNum.keys():
p_v=valueNum[v][0]/dataNum
if not p_v==0:
base+=-p_v*np.log2(p_v)
InfoEntropy=0.0 #特徵A取值為v的信息熵
for y in valueNum[v][1].keys():
p=valueNum[v][1][y]/valueNum[v][0]
if not p==0:
InfoEntropy+=-p*np.log2(p)
ConEntropy+=p_v*InfoEntropy
HDA.append((A,ConEntropy))
Ratio_base.append(base)
'''信息熵與各個特徵的條件熵計算完畢,統計信息增益'''
Gain=[]
for i in range(len(HDA)):
A=HDA[i][0]
G=(HD-HDA[i][1])
if not G==0.0:
G/=Ratio_base[i]
Gain.append((A,G))
return Gain值得一提的是:當信息增益為0時,對應的信息增益率的底數也為0,在編寫函數時需要注意避免分母為0的情況,同時上述兩個算法都可以優化成可以處理具有連續型特徵的數據集的算法,只需要將劃分不同取值分支的過程改為選擇閾值的過程,這也是

最終我們得到的決策樹如下字典所示:可以發現對於我們的西瓜數據集來説兩個算法得到的決策樹相同
#{3: {'清晰': {5: {'硬滑': 1, '軟粘': {4: {'稍凹': {0: {'青綠': 1, '烏黑': 0}}, '平坦': 0}}}}, '稍糊': {5: {'軟粘': 1, '硬滑': 0}}, '模糊': 0}}2.2.5  算法
算法

在ID3算法中我們使用了信息增益來選擇特徵,信息增益大的優先選擇。在C4.5算法中,採用了信息增益率來選擇特徵,以減少信息增益容易選擇特徵值多的特徵的問題。但是無論是ID3還是C4.5,都是基於信息論的熵模型的,這裏面會涉及大量的對數運算。能不能簡化模型同時也不至於完全丟失熵模型的優點呢?當然有!那就是基尼係數!
CART算法使用基尼係數來代替信息增益率,基尼係數代表了模型的不純度,基尼係數越小,則不純度越低,特徵越好。這和信息增益與信息增益率是相反的(它們都是越大越好)。
基尼係數的計算方式如下:數據集為



我們還是以客户流失數據集為例:15條數據中,10條標籤為0,5條標籤為1,則有:

同時還有基於數據集





我們以客户流失數據集為例:
① 性別特徵:15條數據中,8條男性,7條女性;男性數據中,5條標籤0,3條標籤1;女性數據中,5條標籤0,2條標籤1

② 活躍度特徵計算同理:

顯然我們要選擇活躍度特徵,因為它的基尼係數小,不純度更低。
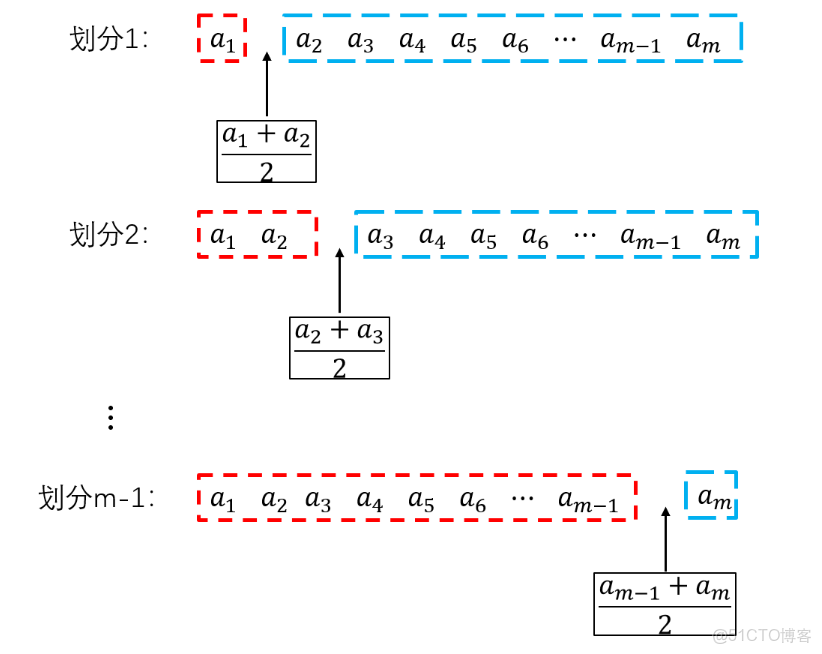
當我們知道如何選擇用於切分的特徵後,應該思考如何在該特徵上選擇一個切分點,即如何尋找一個合適的閾值,在此我們面向連續型特徵進行分析,而對於離散型的數據類比即可。
① 首先,將數據集按照最優特徵從大到小排列
② 對於大小為






③ 每個切分點將數據集劃分為左右兩部分:

找到基尼係數最小的切分方式,選擇切分左右兩個數據點特徵的均值作為閾值。
我們通過代碼實現基於
'''屏蔽warning'''
import warnings
warnings.filterwarnings("ignore")
'''導入重要的庫'''
import numpy as np
import pandas as pd
import copy
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris
'''定義CART決策樹'''
class CART(object):
'''初始化樹模型'''
def __init__(self,data,target):
'''初始化一個用於統計標籤數量的模板'''
self.dictLabel={}
for y in target:
if y not in self.dictLabel.keys():
self.dictLabel[y]=0
'''決策樹模型'''
self.tree=self.buildTree(data,target)
'''構造決策樹'''
def buildTree(self,data,target):
if self.is_same_label(target): #D中所有的標籤都相同
return target[0] #返回相同的標籤
if len(data)==1 or self.is_same_vector(data): #樣本中只有一個特徵或者所有樣本的特徵都一樣
return np.argmax(np.bincount(target)) #返回數量最多的標籤
'''選出基尼係數最小的特徵'''
bestFeature=self.findBestFeature(data,target)
'''選出該特徵最優的劃分'''
threshold=self.findBestSplit(bestFeature,data,target)
'''整合數據集'''
D=[] #整合特徵向量與標籤,便於得到子數據集
for i in range(len(data)):
D.append((data[i],target[i]))
'''劃分數據集'''
dataL,targetL,dataR,targetR=self.splitDataset(bestFeature,threshold,D)
'''構造二叉樹'''
tree={} #初始化樹
tree[(bestFeature,threshold)]={}
'''構造左右子樹'''
tree[(bestFeature,threshold)]["left"]=self.buildTree(dataL,targetL)
tree[(bestFeature,threshold)]["right"]=self.buildTree(dataR,targetR)
return tree
'''計算數據集D的基尼係數'''
def Gini_D(self,target): #我們僅需要target即可計算數據集D的基尼係數
dataNum=len(target) #樣本大小
labelNum=copy.deepcopy(self.dictLabel) #統計各類標籤數量
for y in target:
labelNum[y]+=1
G=1.0 #基尼係數
for y in labelNum.keys():
G-=(labelNum[y]/dataNum)**2
return G
'''計算特徵A的基尼係數'''
def Gini_D_A(self,A,data,target):
dataNum=len(data)
valueNum={} #統計特徵A不同取值信息
'''
valueNum[v]=(num,labelNum)
(num,labelNum)為特徵A取值為v的數據信息
num表示特徵A取值為v的樣本數量
labelNum記錄了特徵A取值為v的樣本中各類標籤
'''
for i in range(dataNum):
value=data[i][A]
label=target[i]
if value not in valueNum:
labelNum=np.array([label])
valueNum[value]=[1,labelNum]
else:
valueNum[value][0]+=1 #取值為value的數量+1
valueNum[value][1]=np.append(valueNum[value][1],label)
'''統計結束,計算特徵A的基尼係數'''
G=0.0 #特徵A的基尼係數
for v in valueNum.keys():
p=valueNum[v][0]/dataNum
G+=p*self.Gini_D(valueNum[v][1])
return G
'''選擇基尼係數最小的特徵'''
def findBestFeature(self,data,target):
featureNum=len(data[0])
Ginis=[] #存儲各個維度的基尼係數
for A in range(featureNum):
Ginis.append((A,self.Gini_D_A(A,data,target)))
Ginis.sort(key=lambda x:x[1]) #按照基尼係數排序
bestFeature=Ginis[0][0]
return bestFeature
'''根據閾值劃分數據集'''
def splitDataset(self,A,threshold,D):
'''
:param A: 用於劃分的特徵
:param threshold: 特徵閾值
:param D: D[i]=(data[i],target[i]),整合後的數據集
:return: 劃分後的左右兩個數據集
'''
'''獲得兩個劃分後的子集'''
DL=np.array(list(filter(lambda x:x[0][A]<threshold,D)))
DR=np.array(list(filter(lambda x:x[0][A]>threshold,D)))
'''分離出data和target'''
dataL=np.array(list(np.array(DL)[:,0]))
targetL=np.array(list(np.array(DL)[:,1]))
dataR=np.array(list(np.array(DR)[:,0]))
targetR=np.array(list(np.array(DR)[:,1]))
return dataL,targetL,dataR,targetR
'''找到最優的劃分'''
def findBestSplit(self,A,data,target):
'''
:param A: 切分點所在的維度
:param data: 特徵向量集
:param target: 標籤集
:return: 該特徵的切分閾值 threshold
'''
dataNum=len(data) #樣本大小
'''首先整合數據'''
D=[] #整合特徵向量與標籤,便於得到子數據集
for i in range(len(data)):
D.append((data[i],target[i]))
'''集合按照特徵A的大小排序'''
D.sort(key=lambda x:x[0][A])
'''遍歷dataNum-1個切分'''
split=[] #存儲各種劃分的基尼係數和閾值,split[i]=(threshold,Gini)
for i in range(dataNum-1):
if D[i][0][A]==D[i+1][0][A]: #取值相同,不進行切分
continue
threshold=(D[i][0][A]+D[i+1][0][A])/2
dataL,targetL,dataR,targetR=self.splitDataset(A,threshold,D)
Gini=(len(dataL)/dataNum)*self.Gini_D(targetL)+(len(dataR)/dataNum)*self.Gini_D(targetR)
split.append((threshold,Gini))
'''選擇基尼係數最小的劃分'''
split.sort(key=lambda x:x[1])
threshold=split[0][0]
return threshold
'''判斷數據集中標籤是否都相同'''
def is_same_label(self,target):
y=target[0]
for i in range(1,len(target)):
if not target[i]==y:
return False
return True
'''判斷數據集中向量是否都相同'''
def is_same_vector(self,data):
x=data[0]
for i in range(1,len(data)):
if not (data[i]==x).all():
return False
return True利用該分類樹的分類器為:
'''定義決策樹分類器'''
class Classifiter(object):
'''無重要參數'''
def __init__(self):
pass
'''訓練模型'''
def fit(self,data,target):
self.decisionTree=CART(data,target) #構造決策樹
'''模型預測'''
def predict(self,X_test):
result=[]
for x_t in X_test:
node=self.decisionTree.tree #node初始化為根節點
while isinstance(node,dict): #只要node不是葉子節點,那麼它一定是字典
feature=list(node.keys())[0][0] #當前決策樹分支特徵
threshold=list(node.keys())[0][1] #當前決策樹分支閾值
if x_t[feature]<threshold:
node=node[(feature,threshold)]["left"]
else:
node=node[(feature,threshold)]["right"]
result.append(node)
return np.array(result)我們可以利用鳶尾花數據集進行模型效果的驗證:可以發現準確率很高,達到了0.96
'''驗證模型效果'''
'''加載鳶尾花數據集'''
iris=load_iris()
data=iris.data
target=iris.target
'''劃分數據集'''
X_train,X_test,y_train,y_test=train_test_split(data,target,test_size=0.2,random_state=10)#選取20%的數據作為測試集
'''初始化模型'''
classifiter=Classifiter()
'''模型訓練與預測'''
classifiter.fit(X_train,y_train)
y_pred=classifiter.predict(X_test)
print(accuracy_score(y_test,y_pred)) #0.9666666666666667可以發現



LightGBM 和 XGBoost 等高性能的第三方庫提供的樹模型具有更強大的性能,適用於機器學習競賽中。