矩陣運算、求導、激活函數、梯度下降算法、反向傳播算法等
1、矩陣運算
如果矩陣${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$,其轉置矩陣${{\mathop{\rm B}\nolimits} = {\left( {{b_{ji}}} \right)_{n \times m}} = {{\mathop{\rm A}\nolimits} ^T}}$的所有元素定義為
${{b_{ji}} = {a_{ij}}{,}\forall {1} \le i \le m{,1} \le j \le n}$
如果矩陣${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$,其旋轉${180^\circ }$為
${rot{\rm{ }}180\left( {\mathop{\rm A}\nolimits} \right) = {\left( {{a_{m - i + 1{,n - }j + 1}}} \right)_{m \times n}}}$
給定兩個矩陣${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{n \times p}}}$,其乘積${{\mathop{\rm C}\nolimits} = {\left( {{c_{ij}}} \right)_{m \times p}} = {\mathop{\rm A}\nolimits} \cdot {\mathop{\rm B}\nolimits} = {\mathop{\rm A}\nolimits} {\mathop{\rm B}\nolimits} }$的所有元素定義為
${{c_{ij}}{\rm{ = }}\sum\limits_{k = 1}^n {{a_{ik}}{b_{kj}}} {,}\forall {1} \le i \le m{,1} \le j \le p}$
給定兩個矩陣${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{m \times n}}}$,其加法和減法為
${{\mathop{\rm A}\nolimits} \pm {\mathop{\rm B}\nolimits} = {\left( {{a_{ij}} \pm {b_{ij}}} \right)_{m \times n}}}$
其阿達瑪積(Hadamard product),又稱為逐元素積定義為
${{\mathop{\rm A}\nolimits} \circ {\mathop{\rm B}\nolimits} = {\left( {{a_{ij}} \times {b_{ij}}} \right)_{m \times n}}}$
給定兩個矩陣${{\mathop{\rm A}\nolimits} = {\left( {{a_{ij}}} \right)_{m \times n}}}$和${{\mathop{\rm B}\nolimits} = {\left( {{b_{ij}}} \right)_{p \times q}}}$,其克羅內克積為
${{\mathop{\rm A}\nolimits} \otimes {\mathop{\rm B}\nolimits} = \left( {\begin{array}{*{20}{c}}
{{a_{11}}{\mathop{\rm B}\nolimits} }& \cdots &{{a_{1n}}{\mathop{\rm B}\nolimits} }\\
\vdots & \ddots & \vdots \\
{{a_{m1}}{\mathop{\rm B}\nolimits} }& \cdots &{{a_{mn}}{\mathop{\rm B}\nolimits} }
\end{array}} \right)}$
如果${{\mathop{\rm x}\nolimits} = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right)^T}}$是向量,那麼一元函數${f\left( x \right)}$的逐元向量函數定義為
${f\left( {\mathop{\rm x}\nolimits} \right) = {\left( {f\left( {{x_1}} \right){,}f\left( {{x_2}} \right){,} \cdots{,}f\left( {{x_n}} \right)} \right)^T}}$
如果${{\mathop{\rm X}\nolimits} = {\left( {{x_{ij}}} \right)_{m \times n}}}$是矩陣,那麼一元函數${f\left( x \right)}$的逐元矩陣函數定義為
${f\left( {\mathop{\rm X}\nolimits} \right) = {\left( {f\left( {{x_{ij}}} \right)} \right)_{m \times n}}}$
2、導數公式
如果${{\mathop{\rm x}\nolimits} = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right)^T}}$,那麼逐元向量函數的導數為
${f'\left( {\mathop{\rm x}\nolimits} \right) = {\left( {f'\left( {{x_1}} \right){,}f'\left( {{x_2}} \right){,} \cdots {,}f'\left( {{x_n}} \right)} \right)^T}}$
如果${{\mathop{\rm X}\nolimits} = {\left( {{x_{ij}}} \right)_{m \times n}}}$,那麼逐元矩陣函數的導數為
${f'\left( {\mathop{\rm X}\nolimits} \right) = {\left( {f'\left( {{x_{ij}}} \right)} \right)_{m \times n}}}$
如果a、b、c和x是n維向量,A、B、C和X是n階矩陣,那麼
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm x}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = \frac{{\partial \left( {{{\mathop{\rm x}\nolimits} ^T}{\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = {\mathop{\rm a}\nolimits} }$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm a}\nolimits} {{\mathop{\rm b}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = \frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm a}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm a}\nolimits} {{\mathop{\rm a}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm a}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {\mathop{\rm X}\nolimits} \left( {{\mathop{\rm a}\nolimits} {{\mathop{\rm b}\nolimits} ^T} + {{\mathop{\rm a}\nolimits} ^T}{\mathop{\rm b}\nolimits} } \right)}$
${\frac{{\partial \left( {{{\left( {{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm a}\nolimits} } \right)}^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm B}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm b}\nolimits} } \right)} \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = {{\mathop{\rm A}\nolimits} ^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm B}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm b}\nolimits} } \right) + {{\mathop{\rm B}\nolimits} ^T}{\mathop{\rm C}\nolimits} \left( {{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} + {\mathop{\rm a}\nolimits} } \right)}$
${\frac{{\partial \left( {{{\mathop{\rm x}\nolimits} ^T}{\mathop{\rm A}\nolimits} {\mathop{\rm x}\nolimits} } \right)}}{{\partial {\mathop{\rm x}\nolimits} }} = \left( {{\mathop{\rm A}\nolimits} + {{\mathop{\rm A}\nolimits} ^T}} \right){\mathop{\rm x}\nolimits}}$
${\frac{{\partial \left( {{{\left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right)}^T}{\mathop{\rm A}\nolimits} \left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right)} \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = \left( {{\mathop{\rm A}\nolimits} + {{\mathop{\rm A}\nolimits} ^T}} \right)\left( {{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} + {\mathop{\rm c}\nolimits} } \right){{\mathop{\rm b}\nolimits} ^T}}$
${\frac{{\partial \left( {{{\mathop{\rm b}\nolimits} ^T}{{\mathop{\rm X}\nolimits} ^T}{\mathop{\rm A}\nolimits} {\mathop{\rm X}\nolimits} {\mathop{\rm c}\nolimits} } \right)}}{{\partial {\mathop{\rm X}\nolimits} }} = {{\mathop{\rm A}\nolimits} ^T}{\mathop{\rm X}\nolimits} {\mathop{\rm b}\nolimits} {{\mathop{\rm c}\nolimits} ^T} + {\mathop{\rm A}\nolimits} {\mathop{\rm X}\nolimits} {\mathop{\rm c}\nolimits} {{\mathop{\rm b}\nolimits} ^T}}$
3、激活函數
sigmoid函數:
${\sigma \left( x \right) = sigm\left( x \right) = \frac{1}{{1 + {e^{ - x}}}}}$
導數:
${\sigma '\left( x \right) = \left( {sigm\left( x \right)} \right)' = \sigma \left( x \right)\left( {1 - \sigma \left( x \right)} \right) = - \frac{{{e^{ - x}}}}{{{{\left( {1 + {e^{ - x}}} \right)}^2}}}}$
雙曲正切函數tanh:
${tanh\left( x \right) = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}}$
導數:
${\left( {tanh\left( x \right)} \right)' = 1 - {\left( {tanh\left( x \right)} \right)^2} = \frac{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2} - {{\left( {{e^x} - {e^{ - x}}} \right)}^2}}}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}}}$
修正線性單元ReLU:
${ReLU\left( x \right) = max\left( {0{,}x} \right)}$
滲漏修正線性單元LReLU:
${LReLU\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
{1{,}x \ge 0}\\
{ax{,}x < 0}
\end{array}} \right.}$
軟最大輸出函數softmax:
${softmax\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_n}} \right) = \frac{1}{{\sum\limits_{i = 1}^n {exp\left( {{x_i}} \right)} }}{\left( {exp\left( {{x_i}} \right)} \right)_{n \times 1}}}$
4、梯度下降算法
梯度下降算法,是在無約束條件下計算連續可微函數極小值的基本方法。這種方法的核心思想是用
負梯度方向作為下降方向,在1874年由法國科學家Cauchy提出。
輸入:${f\left( x \right)}$的表達式
輸出:極小值點${{x^ * }}$
1. 選初始點${{x_0}}$,收斂誤差${\varepsilon > 0}$,迭代次數為N,令k=0。
2. 若${\left| {\nabla f\left( {{x_k}} \right)} \right| \le \varepsilon }$,則${{x^ * } = {x_k}}$,停止迭代;否則計算${{\nabla f\left( {{x_k}} \right)}}$。
3. 選擇和計算步長因子${{\alpha _k}}$。
4. 計算${{x_{k + 1}} = {x_k} - {\alpha _k}\nabla f\left( {{x_k}} \right)}$。
5. 令k=k+1,若${k \ge N}$,則${{x^ * } = {x_k}}$,停止迭代;否則轉至步驟2。
隨機梯度下降算法 (SGD)
採用嚴格的反向傳播算法訓練神經網絡,需要同時考慮所有樣本對梯度的貢獻。如果樣本的數量很大,那麼梯度下降的每一次迭代都可能花費很長時間,從而可能導致整個過程收斂得非常緩慢。
隨機梯度下降(Stochastic Gradient Descent,SGD)是一種對梯度下降優化方法的隨機近似。其應用條件是目標函數能夠表示成一組可微函數之和。
1)在線模式
在線模式是先把所有樣本隨機洗牌,再逐一計算每個樣本對梯度的貢獻去更新權值,即
${{w} = {w} - \eta \frac{{\partial {e_i}}}{{\partial {w}}}{,}l = 1{,}2{,} \cdots {,}L}$
其中,${{e_i}}$表示網絡計算樣本${{{x}^l}}$的實際輸出與期望輸出之間的誤差。注意,這個按樣本逐一更新權值的過程可能需要循環多次。
2) mini-batch 模式
在線模式的缺點是梯度下降的過程不太穩定、波動較大。一種折中的方法是採用“迷你塊”mini-batch模式,實際上就是把所有樣本隨機洗牌後分為若干大小為m的塊,再逐一計算每塊對梯度的貢獻去更新權值,即
${{w} = {w} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {w}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
為了改善隨機梯度下降的訓練效果,還常常使用權值衰減(weight decay)係數${\lambda}$,可得到
${{w} = \left( {1 - \lambda } \right){w} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {w}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
為了進一步提高穩定性,可以再引入一個動量項d及其加權係數${v}$,得到SGD的基本動量模式:
${{{d}_{l + 1}} = v{{d}_l} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {{w}_l}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor {,}v > 0}$
${{{w}_{l + 1}} = \left( {1 - \lambda } \right){{w}_l}{ } + {{d}_{l + 1}} = \left( {1 - \lambda } \right){{w}_l} + v{{d}_l} - \eta \left[ {\frac{1}{m}\sum\limits_{l = \left( {i - 1} \right) \cdot m + 1}^{i \cdot m} {\frac{{\partial {e_l}}}{{\partial {{w}_l}}}} } \right]{,}i = 1{,}2{,} \cdots {,}\left\lfloor {L/m} \right\rfloor}$
注
隨機梯度下降還有很多其他變種,重要包絡Nesterov動量模式、Adagrad、Adadelta、RMSProp和Adam等。其中,Adam是目前最好的算法。
5、反向傳播算法
深度神經網絡的基本學習訓練方法是反向傳播算法,反向傳播算法在本質上是一種具有遞歸結構的梯度下降算法,往往需要給定足夠多的訓練樣本,才能獲得滿意的效果。
1)逐層反向傳播算法
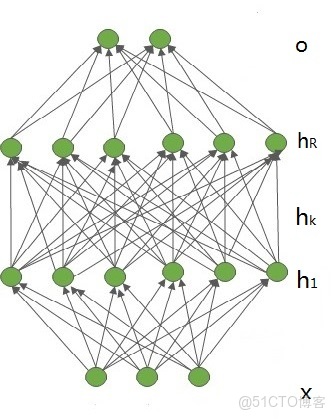
多層感知器由一個輸入層、若干隱含層和一個輸出層組成,如圖所示。不妨設輸入層的維數是m,輸入向量表示為${x = {\left( {{x_1}{,}{x_2}{,} \cdots{,}{x_m}} \right)^T} \in {R^m}}$。第k個隱含層包含${{n_k}}$個神經元${\left( {k = 1{,}2{,} \cdots {,}R} \right)}$,相應的隱含層向量表示為${{{h}_k} = {\left( {{h_{k,1}}{,}{h_{k,2}}{,} \cdots{,}{h_{k,{n_k}}}} \right)^T} \in {R^{{n_k}}}}$。輸出層包含c個神經元,輸出向量表示為${{o} = {\left( {{o_1}{,}{o_2}{,} \cdots {,}{o_c}} \right)^T} \in {R^c}}$。輸入層與第1個隱含層之間的權值矩陣用${{{W}^1} = {\left( {w_{ij}^1} \right)_{{n_1} \times m}}}$表示。第k-1個隱含層與第k個隱含層之間的權值矩陣用${{{W}^k} = {\left( {w_{ij}^k} \right)_{{n_k} \times {n_{k - 1}}}}\left( {1 < k \le R} \right)}$表示。第R個隱含層與輸出層之間的權值矩陣用${{{W}^{R + 1}} = {\left( {w_{ij}^{R + 1}} \right)_{c \times {n_R}}}}$表示。那麼,這個多層感知器的各層神經元激活輸出可以計算如下:
${\left\{ {\begin{array}{*{20}{c}}{{{h}_1} = {\sigma _{{{h}_1}}}\left( {{{W}^1}{x + }{{b}^1}} \right)}\\
{{{h}_k} = {\sigma _{{{h}_k}}}\left( {{{W}^k}{{h}_{k - 1}}{ + }{{b}^k}} \right){,}2}\\
{{o} = {\sigma _{o}}\left( {{{W}^{R + 1}}{{h}_R}{ + }{{b}^{R + 1}}} \right)}
\end{array}} \right. \le k \le R}$
其中,${{{b}^1}}$、${{{b}^k}}$和${{{{b}^{R + 1}}}}$是各層的偏置;${{{\sigma _{{{h}_1}}}}}$、${{{\sigma _{{{h}_k}}}}}$和${{{\sigma _{o}}}}$是各層的逐元向量函數,一般都取為逐元sigmoid函數。
輸入:訓練集${\left\{ {\left( {{{x}^l},{{y}^l}} \right),{\rm{ 1}} \le l \le {\rm{L}}} \right\}}$,學習率${\eta }$,分層網絡結構,迭代次數 epoch。
輸出:所有權值和偏置${\left( {{{W}^k}{,}{{b}^k}} \right)\left( {1 \le k \le R + 1} \right)}$
1. 隨機初始化${{{W}^k} \approx 0}$,${{{b}^k} \approx 0}$,${k = 1{,}2{,} \cdots {,}R + 1}$
2. 令${{h}_0^l = {x^l}}$
3. for ${i = 1{,}2{,} \cdots {,}epoch}$ do
4. for ${l = 1{,}2{,} \cdots {,}L}$ do
5. 計算${{u}_k^l = {{W}^k}{h}_{k - 1}^l + {{b}^k}}$,${{h}_k^l = \sigma \left( {{u}_k^l} \right)}$,${{1 \le k \le R + 1}}$
6. 計算${{\delta }_{R + 1}^l = \left( {{{o}^l} - {{y}^l}} \right) \circ \sigma '\left( {{u}_{R + 1}^l} \right)}$
7. 計算${{\delta }_k^l = \left[ {{{\left( {{{W}^{k + 1}}} \right)}^T}{\delta }_{k + 1}^l} \right] \circ \sigma '\left( {{u}_k^l} \right){,}1 \le k \le R}$
8. end for
9. 計算${\frac{{\partial E}}{{\partial {{W}^k}}} = \sum\limits_{l = 1}^L {{\delta }_k^l{{\left( {{h}_{k - 1}^l} \right)}^T}} }$,${\frac{{\partial E}}{{\partial {{b}^k}}} = \sum\limits_{l = 1}^L {{\delta }_k^l} }$,${1 \le k \le R + 1}$
10. 如果總梯度足夠小,則停止
11. 否則,更新權值和偏置:${{{W}^k} \leftarrow {{W}^k} - \eta \frac{{\partial {L_N}}}{{\partial {{W}^k}}}}$,${{{b}^k} \leftarrow {{b}^k} - \eta \frac{{\partial {L_N}}}{{\partial {{b}^k}}}}$,${1 \le k \le R + 1}$
12. end for
2)誤差函數
平方誤差
為了對多層感知器中的權值和偏置進行學習,需要給定一組訓練樣本。假定共有L個訓練樣本${\left( {{{x}^l}{,}{{y}^k}} \right)\left( {1 \le l \le L} \right)}$,輸入是${{{x}^l} = {\left( {{x}_1^l{,}{x}_2^l{,} \cdots {,}{x}_m^l} \right)^T}}$,期望輸出是${{{y}^l} = {\left( {{y}_1^l{,}{y}_2^l{,} \cdots {,}{y}_c^l} \right)^T}}$,實際輸出是${{{o}^l} = {\left( {o_1^l{,}o_2^l{,} \cdots {,}o_c^l} \right)^T}}$。把優化的目標函數選為平方誤差:
${E = \frac{1}{2}\sum\limits_{l = 1}^L {{{\left\| {{{o}^l} - {{y}^l}} \right\|}^2}} = \frac{1}{2}\sum\limits_{l = 1}^L {\sum\limits_{j = 1}^c {{{\left\| {{o}_j^l - {y}_{^j}^l} \right\|}^2}} } }$
令${{h}_0^l = {{x}^l}}$,${{u}_k^l = {{W}^k}{h}_{k - 1}^l + {{b}^k}}$,${{h}_k^l = \sigma \left( {{u}_k^l} \right)\left( {1 \le k \le R + 1} \right)}$,${{{o}^l} = {h}_{R + 1}^l = \sigma \left( {{u}_{R + 1}^l} \right)}$。如果定義網絡各層關於第${l}$個樣本的反向傳播誤差信號的靈敏度為:
${\delta _k^l = \frac{{\partial E}}{{\partial {u}_k^l}}}$
那麼這些反向傳播誤差信號可依次計算如下:
${\delta _{R + 1}^l = \frac{{\partial E}}{{\partial {u}_{R + 1}^l}} = \frac{{\partial E}}{{\partial {{o}^l}}} \cdot \frac{{\partial {{o}^l}}}{{\partial {u}_{R + 1}^l}} = \left( {{{o}^l} - {{y}^l}} \right) \circ \sigma '\left( {{u}_{R + 1}^l} \right) = \left( {{{o}^l} - {{y}^l}} \right) \circ {{o}^l} \circ \left( {1 - {{o}^l}} \right)}$
${\delta _k^l = \frac{{\partial E}}{{\partial {u}_k^l}} = \frac{{\partial E}}{{\partial {u}_{k + 1}^l}} \cdot \frac{{\partial {u}_{k + 1}^l}}{{\partial {u}_k^l}} = \left[ {{{\left( {{{W}^{k + 1}}} \right)}^T}\delta _{k + 1}^l} \right] \circ \sigma '\left( {{u}_k^l} \right){,1} \le {k} \le {R}}$
根據上式,可以總結為逐層反向傳播算法。
交叉熵誤差
${E = - \sum\limits_{l = 1}^L {\sum\limits_{j = 1}^c {\left( {{y}_{^j}^l \times log\left( {{o}_j^l} \right) + \left( {1 - {y}_{^j}^l} \right) \times log\left( {1 - {o}_j^l} \right)} \right)} } }$
這時,相應的逐層反向傳播算法只需把${\delta _{R + 1}^l}$的計算公式修改為:
${\delta _{R + 1}^l = {{o}^l} - {{y}^l}}$
注
需要指出的是,多層感知器在訓練完成之後,常常再被用軟最大函數softmax轉換為偽概率輸出:
${{o} = softmax\left( {{{W}^{R + 1}}{{h}_R} + {{b}^{R + 1}}} \right)}$
若採用平方誤差作為目標函數時, ${\delta _{R + 1}^l}$ 的計算公式改為:
${\delta _{R + 1}^l = \frac{{\partial E}}{{\partial {u}_{R + 1}^l}} = \frac{{\partial E}}{{\partial {{o}^l}}} \cdot \frac{{\partial {{o}^l}}}{{\partial {u}_{R + 1}^l}} = \left[ {diag\left( {{{o}^l}} \right) - {{o}^l}{{\left( {{{o}^l}} \right)}^T}} \right]\left( {{{o}^l} - {{y}^l}} \right)}$
若採用交叉熵誤差作為目標函數時, ${\delta _{R + 1}^l}$ 的計算公式改為:
${\delta _{R + 1}^l = \left( {\begin{array}{*{20}{c}}
1&{\frac{{o_1^l}}{{o_2^l - 1}}}& \cdots &{\frac{{o_1^l}}{{o_c^l - 1}}}\\
{\frac{{o_2^l}}{{o_1^l - 1}}}&1& \cdots &{\frac{{o_2^l}}{{o_c^l - 1}}}\\
\vdots & \vdots & \vdots & \vdots \\
{\frac{{o_c^l}}{{o_1^l - 1}}}&{\frac{{o_c^l}}{{o_2^l - 1}}}& \cdots &1
\end{array}} \right)\left( {{{o}^l} - {{y}^l}} \right)}$
${= \left( {diag\left( {1./\left( {1 - {{o}^l}} \right)} \right) - {{\left( {{{o}^l}} \right)}^T}\left( {1./\left( {1 - {{o}^l}} \right)} \right)} \right)\left( {{{o}^l} - {{y}^l}} \right)}$
其中,“1”表示一個分量全是1的向量,“./”表示向量的對應分量相除。
如果每個樣本的期望輸出${{{{y}^l}}}$僅有一個分量,為${{y}_{jl}^l = 1}$,那麼還可以選用退化交叉熵作為目標函數,即:
${E = - \sum\limits_{l = 1}^L {log\left( {o_{jl}^l} \right)} }$
同時,${\delta _{R + 1}^l}$ 的計算公式應修正為:
${\delta _{R + 1}^l = {{o}^l} - {{y}^l}}$
6、塊歸一化(batch normalization)
塊歸一化,又稱為批量歸一化。對神經網絡的訓練過程進行塊歸一化,不僅可以提高網絡的訓練速度,還可以提高網絡的泛化能力。塊歸一化可以理解為把對輸入數據的歸一化擴展到其他層的輸入數據進行歸一化,以減小內部數據分佈偏移的影響。經過塊歸一化後,一方面可以通過選擇比較大的初始學習率極大提升訓練速度,另一方面還可以不用太關心初始化方法和正則化技巧的選擇,從而減少對網絡訓練過程的人工干預。
塊歸一化在理論上可以作用於任何變量,但在神經網絡中一般直接作用隱含層單元的輸入,不妨設x表示某個隱含層單元的輸入。${B = \left\{ {\left. {{x_1}{,}{x_2}{,} \cdots {,}{x_m}} \right\}} \right.}$表示x的一個取值塊。塊歸一化實際上是學習一個包含兩個參數${\gamma}$和${\beta}$的變換${B{N_{\gamma {,}\beta }}}$,把${{x_i}}$變成${{y_i}}$,計算過程如下:
${\left\{ {\begin{array}{*{20}{c}}
{{\mu _B} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} }\\
{{\sigma _B} \leftarrow \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{x_i} - {\mu _B}} \right)}^2}} }\\
{{{\hat x}_i} \leftarrow \frac{{{x_i} - {\mu _B}}}{{\sqrt {\sigma _{_B}^2 + \varepsilon } }}}\\
{{y_i} \leftarrow \gamma {{\hat x}_i} + \beta \equiv B{N_{\gamma {,}\beta }}\left( {{{\hat x}_i}} \right)}
\end{array}} \right.}$
在學習訓練完成之後,令均值${E\left[ x \right] = {E_B}\left[ {{\mu _B}} \right]}$、方差${V\left[ x \right] = \frac{m}{{m - 1}}{E_B}\left[ {\sigma _B^2} \right]}$,並把變換${y = B{N_{\gamma {,}\beta }}\left( {{{\hat x}_i}} \right)}$替換成下面的推理尺度變換:
${y = \frac{\gamma }{{\sqrt {V\left[ x \right] + \varepsilon } }} \cdot x + \left( {\beta - \frac{{\gamma E\left[ x \right]}}{{\sqrt {V\left[ x \right] + \varepsilon } }}} \right)}$
在應用時,塊歸一化通常被直接作用於某個或多個隱含層的所有輸入。
7、權值偏置初始化
在訓練神經網絡之前,必須對其權值和偏置進行初始化。常用的初始化方法有三種:高斯初始化、Xavier初始化和MSRA初始化。它們一把都把偏置初始化為0,但對權值進行隨機初始化。
1)高斯初始化
權值:根據高斯分佈初始化,均值選為0, 方差人工選擇。
2)Xavier初始化
如果神經元有n個輸入,則${{{w}_{ij}} \sim U\left[ { - \frac{1}{{\sqrt N }}{,}\frac{1}{{\sqrt N }}} \right]}$,b=0。
3)MSRA初始化
如果神經元有n個輸入,則 ${{{w}_{ij}} \sim N\left[ {0{,}\frac{2}{n}} \right]}$,b=0。
8、權值丟失(dropout)
在訓練神經網絡時,如果訓練樣本較少,一般就需要考慮採用某些正則化技巧來防止過擬合。權值丟失是一種簡單有效的正則化技巧,其基本思想是通過阻止特徵檢測器的共同作用來提高神經網絡的泛化能力。主要包括丟失輸出和丟失連接。
1)丟失輸出
丟失輸出是指在神經網絡的訓練過程中隨機讓網絡的某些節點(包括輸入和隱含節點)不工作。
2)丟失連接
丟失連接是指在神經網絡的訓練過程中隨機讓網絡的某些連接不工作。
參考文獻
[1] 李玉鑑等. 深度學習:卷積神經網絡從入門到精通, 北京:機械工業出版社,2018.