【題目來源】
https://www.luogu.com.cn/problem/P1330
【題目描述】
曹是一隻愛刷街的老曹，暑假期間，他每天都歡快地在陽光大學的校園裏刷街。河蟹看到歡快的曹，感到不爽。河蟹決定封鎖陽光大學，不讓曹刷街。
陽光大學的校園是一張由 n 個點構成的無向圖，n 個點之間由 m 條道路連接。每隻河蟹行對一個點進行封鎖，當某個點被封鎖後，與這個點相連的道路就被封鎖了，曹就無法在這些道路上刷街了。特別悲劇的一點是，河蟹是一種不和諧的生物，當兩隻河蟹封鎖了相鄰的兩個點時，他們會發生衝突。
詢問：最少需要多少隻河蟹，能夠封鎖所有道路並且不發生衝突。

【輸入格式】
第一行兩個正整數，表示節點數和邊數。 接下來 m 行，每行兩個整數 u，v，表示點 u 到點 v 之間有道路相連。

【輸出格式】
僅一行。如果河蟹無法封鎖所有道路，則輸出 Impossible，否則輸出一個整數，表示最少需要多少隻河蟹。

【輸入樣例一】
3 3
1 2
1 3
2 3

【輸出樣例一】
Impossible

【輸入樣例二】
3 2
1 2
2 3

【輸出樣例二】
1

【材料範圍】
對於 100% 的數據，1≤n≤10^4，1≤m≤10^5，保證沒有重邊。

【算法分析】
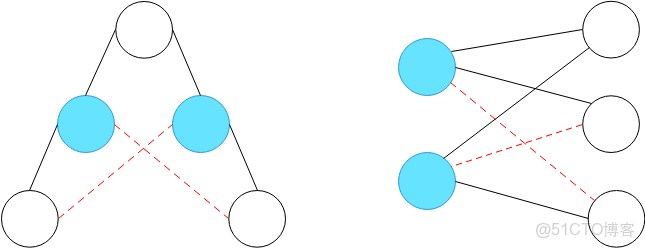
● 二分圖的概念：如果無向圖 G=(V, E) 的所有點可以分為兩個集合 V1，V2，所有邊都在 V1 與 V2 之間，且 V1，V2 的內部都沒有邊，則稱 G 是一個二分圖。

● 一個圖是否為二分圖，一般用“染色法”進行判斷。染色法的核心思想非常直觀：嘗試用兩種顏色對圖中的所有頂點進行着色，並確保任何一條邊兩端的頂點顏色都不相同。如果能成功完成着色，則該圖是二分圖；否則，不是。

● 染色法的染色邏輯
（1）運用兩種顏色：顏色 1 和顏色 2。
（2）若當前節點染色為 c，相鄰節點必須染為 3^c（即 3-c）。這是因為，3^1=2，3^2=1，故通過異或運算可實現顏色切換。

● 染色法的算法流程通常基於 BFS 或 DFS 實現。
（1）選擇一種顏色（如 1）作為起始顏色。
（2）從一個未訪問的節點開始，將其染色，然後遍歷其所有鄰居。
（3）若鄰居未染色，則將其染成與當前節點相反的顏色（如 2），並遞歸（DFS）或入隊（BFS）處理。
（4）若鄰居已染色，則檢查其顏色是否與當前節點相反。若顏色相同，則説明存在奇環，該圖不是二分圖。

● 樹結構天然是二分圖
（1）無環性：樹是無環連通圖，因此不可能存在奇數環。
（2）層次結構：從任意根節點開始，奇偶層自然形成兩個獨立集合。
（2）可二染色性：樹可以用兩種顏色進行頂點着色，使得相鄰頂點顏色不同。

● 由於樹本身是二分圖，節點允許染成兩種顏色。設樹的節點數為 n，其中一種顏色的節點數為 m，若保證增邊後的圖形仍是二分圖，則最大可增加的邊數為m*(n-m)-(n-1)。其中，m*(n-m) 為完全二分圖的最大邊數 ，n-1 為樹的邊數。

【算法代碼】
本題代碼大部分與“AcWing 860：染色法判定二分圖”相同。詳見：

#include 
using namespace std;
const int N=1e4+5;
const int M=1e5+5;
int e[M<<1],ne[M<<1],h[N],idx;
int color[N];
int cnt[3],ans;
int n,m;
void add(int a,int b) {
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
//Dye node u with color c
bool dye(int u,int c) {
    color[u]=c,cnt[c]++;
    for(int i=h[u]; i!=-1; i=ne[i]) {
        int j=e[i];
        if(!color[j]) { //3^1=2,3^2=1
            if(!dye(j,3^c)) return false;
        } else if(color[j]==c) return false;
    }
    return true;
}
int main() {
    memset(h,-1,sizeof h);
    cin>>n>>m;
    while(m--) {
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }
    bool flag=true;
    for(int i=1; i<=n; i++) {
        cnt[2]=cnt[1]=0;
        if(!color[i]) {
            if(!dye(i,1)) {
                flag=false;
                break;
            }
        }
        ans+=min(cnt[1],cnt[2]);
    }
    if(flag) cout<