目錄
一、序列式容器與關聯式容器
二、pair結構介紹
1. 類的定義
2. 構造方法
3. 比較操作
三、set / multiset 的使用
1. set 與 multiset的介紹
2. set的成員函數
(1)構造與迭代器
(2)增刪查
(3)其他成員函數
3. multiset 的不同特徵
(1)insert
(2)find
(3)erase
(4)count
(5)lower_bound / upper_bound
(6)equal_range - 相等範圍
4. 練習
四、map / multimap 的使用
1. map 與 multimap的介紹
2. map的成員函數
(1)構造與迭代器
(2)增刪查
(3)operator[ ]
(4)其他成員函數
3. multimap 的不同特徵
4. 練習
五、unordered_(multi)set 與 unordered_(multi)map 的使用
1. 容器介紹
2. 和(multi)set、(multi)map的區別
3. 增加的成員函數
4. 練習
六、紅黑樹封裝 set 與 map
1. 泛型編程的應用
2. iterator的實現
3. insert的實現
4. 完整代碼
七、哈希表封裝 unordered_set 與 unordered_map
1. 整體概述
2. iterator的實現
3. 完整代碼
一、序列式容器與關聯式容器
在 C++ STL 中,容器分為兩大類:
序列式容器:如 string、vector、list、deque 等,這些容器的元素按存儲位置順序保存和訪問,元素之間沒有緊密的關聯關係。
關聯式容器:如 map/set 系列和 unordered_map/unordered_set 系列,這些容器的邏輯結構通常是非線性的,元素之間有關聯關係,元素按關鍵字保存和訪問。
本章重點介紹基於紅黑樹實現的 set 和 map,和基於哈希表實現的unordered_set / unordered_map,***set 適用於 key 搜索場景,***map 適用於 key/value 搜索場景。
二、pair結構介紹
1. 類的定義
std::pair 是一個模板類,定義在 <utility> 頭文件中,用於存儲兩個可能不同類型的值。
template <class T1, class T2>
struct pair {
T1 first;
T2 second;
};
- 訪問第一個元素 p.first
- 訪問第二個元素 p.second
2. 構造方法
void test_pair()
{
// 1. 默認構造 - 成員使用默認值
std::pair<int, std::string> p1;
// 2. 直接值構造
std::pair<int, std::string> p2(42, "hello");
std::cout << p2.first << ", \"" << p2.second << "\")" << std::endl;
// 3. 拷貝構造
std::pair<int, std::string> p3(p2);
std::cout << p3.first << ", \"" << p3.second << "\")" << std::endl;
// 4. 使用 make_pair (自動類型推導)
auto p6 = std::make_pair(123, "auto deduction");
std::cout << p6.first << ", \"" << p6.second << "\")" << std::endl;
// 5. 統一初始化 (C++11)
std::pair<int, std::string> p7{ 999, "uniform init" };
std::cout << p7.first << ", \"" << p7.second << "\")" << std::endl;
// 6. 賦值初始化
std::pair<int, std::string> p8 = { 888, "assignment init" };
std::cout << p8.first << ", \"" << p8.second << "\")" << std::endl;
}3. 比較操作
pair是支持比較的,這是默認的比較規則:
當然,我們也能自己寫仿函數,比如:
struct PairCompare {
// 先比較 first,如果 first 相等再比較 second
template <typename T1, typename T2>
bool operator()(const std::pair<T1, T2>& lhs, const std::pair<T1, T2>& rhs) const {
if (lhs.first != rhs.first) {
return lhs.first < rhs.first; // 先按 first 升序
}
return lhs.second > rhs.second; // first 相等時按 second 降序
}
};三、set / multiset 的使用
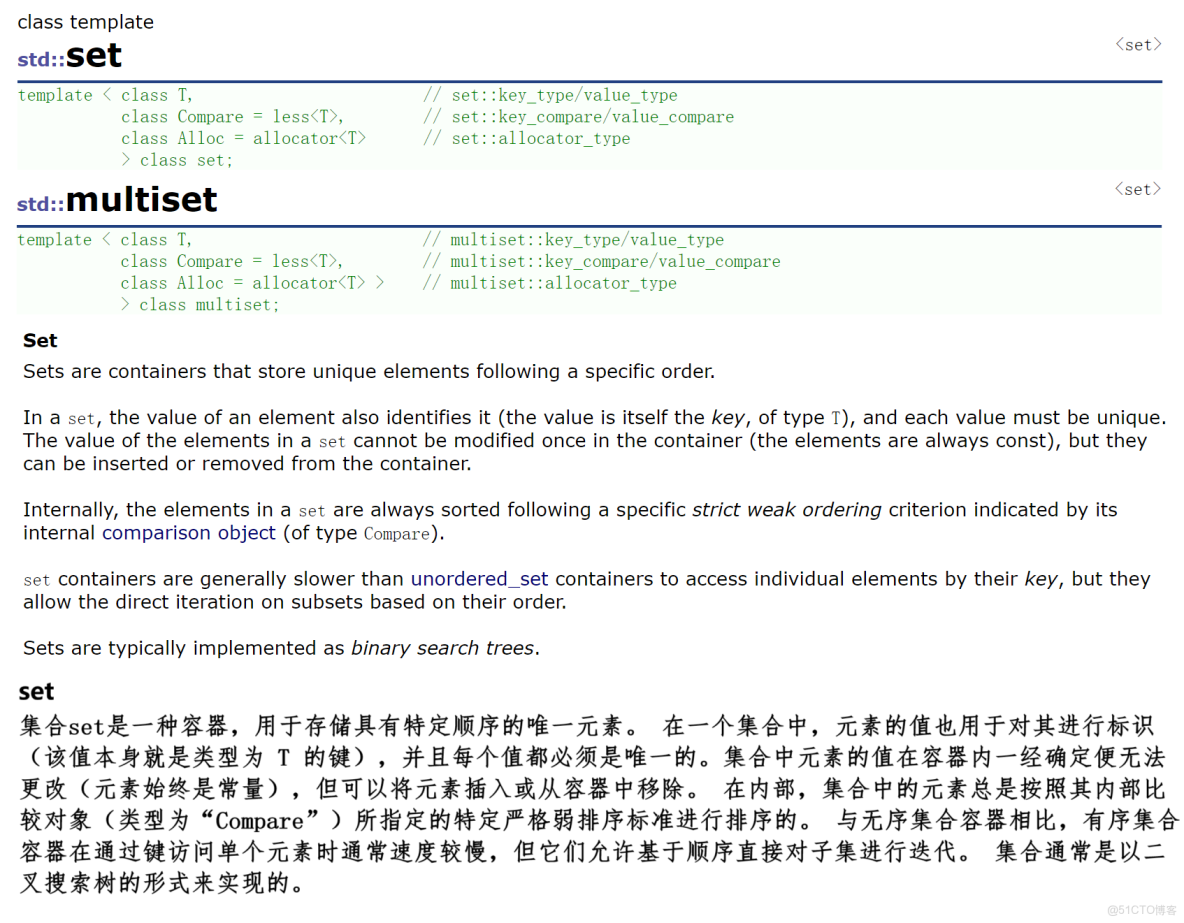
1. set 與 multiset的介紹
- T:set 底層關鍵字的類型
- Compare:比較函數,默認是 less<T>
- Alloc:空間配置器,默認是 allocator<T>
set / multiset 底層使用紅黑樹實現,增刪查效率為 O(logN),迭代器遍歷按中序遍歷,因此是有序的。用一句話總結它們的作用就是自動維護一個的集合,保證它有序,set集合裏沒有重複值,而multiset可以存儲重複值。
2. set的成員函數
(1)構造與迭代器
set的迭代器是 雙向迭代器 且是 常量迭代器,只能讀,不能修改元素值(因為會破壞內部的紅黑樹結構)。下面是用法和示例:
void test1()
{
// 1. 默認構造:創建一個空的set
std::set<int> s1;
// 2. 迭代器範圍構造:用 [first, last) 區間內的元素構造
std::vector<int> v = { 5, 2, 3, 2, 5 };
std::set<int> s2(v.begin(), v.end()); // s2: {2, 3, 5} (自動去重排序)
// 3. 拷貝構造:用一個set初始化另一個
std::set<int> s3(s2);
// 4. 初始化列表構造 (C++11)
std::set<int> s4 = { 1, 4, 2, 1, 3 }; // s4: {1, 2, 3, 4}
// 正向迭代器 (順序為排序後的順序:1, 2, 3, 4)
for (auto it = s4.begin(); it != s4.end(); ++it) {
std::cout << *it << " "; // 可以讀 *it
// *it = 10; // 錯誤!不能修改
}
for (const auto& val : s4) {
std::cout << val << " ";
}
// 反向迭代器 (順序為 4, 3, 2, 1)
for (auto rit = s4.rbegin(); rit != s4.rend(); ++rit) {
std::cout << *rit << " ";
}
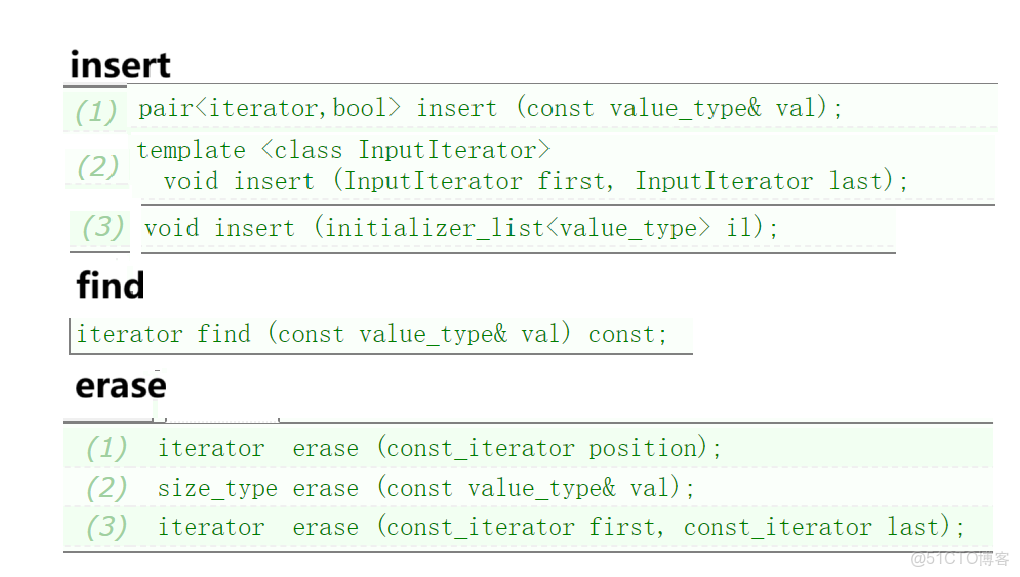
}(2)增刪查
- insert(1):插入一個值,返回值是pair<frist,second>,如果該值已經存在,frist返回它的迭代器,second返回false;如果不存在,frist返回新值的迭代器,second返回true。
- find: 查找val,返回val所在的迭代器,沒有找到返回end() 。
- erase(2): 刪除val,val不存在返回0,存在返回1。
- 返回iterator的erase,要注意迭代器失效問題,和以前講的一樣。
- set不能修改。
void test2()
{
set<int> s;
// 1. 插入單個值,返回 pair<iterator, bool>
auto ret = s.insert(5);
// 2. 插入一個迭代器範圍
std::vector<int> v = { 2, 7, 2, 3 };
s.insert(v.begin(), v.end());
// 3. 使用初始化列表插入
s.insert({ 8, 1, 6 });
for (const auto& val : s) {
cout << val << " ";
}
auto it = s.find(3);
// 1. 通過迭代器位置刪除
if (it != s.end())
s.erase(it); // 刪除元素 3
// 2. 通過值刪除,返回刪除的元素個數 (對於set,只能是0或1)
size_t count = s.erase(2);
// 3. 刪除一個迭代器範圍 [first, last)
s.erase(s.begin(), ++s.begin()); // 刪除前兩個元素
for (const auto& val : s) {
cout << val << " ";
}
}
/*
1 2 3 5 6 7 8
7
5 6 7 8
1
*/(3)其他成員函數
- count:返回具有特定鍵的元素數量。對於set,返回值只能是 0 或 1,用於檢查元素是否存在。(我們以前説的Key-Value模型,Key就是鍵,Value就是值,合起來叫鍵值對,只不過set鍵就是值)
- lower_bound:返回一個迭代器,指向 第一個不小於(即大於或等於)給定鍵的元素。
- upper_bound:返回一個迭代器,指向 第一個大於 給定鍵的元素。
- equal_range:放到multiset那裏講。
void test3()
{
set<int> s = { 10, 20, 30, 40 };
auto it_low = s.lower_bound(30); //30
auto it_up = s.upper_bound(25); //30
auto it_up2 = s.upper_bound(30); //40
if (s.count(20) == 1) {
cout << "Element 220 exists." << endl;
}
}3. multiset 的不同特徵
multiset允許鍵重複,這是與set整體上的唯一區別
(1)insert
multiset::insert總是成功,返回iterator而不是pair<iterator, bool>。
std::multiset<int> ms;
auto ret = ms.insert(5); // 返回 iterator (不是pair!)
// 總是插入成功,返回指向新插入元素的迭代器
ms.insert(5); // 可以重複插入相同的值
ms.insert(5); // 再插入一個5
// ms 現在包含: 5, 5, 5(2)find
當存在重複元素時,
multiset::find返回第一個匹配元素的迭代器。
std::multiset<int> ms = {1, 2, 2, 3, 3, 3};
// 存儲: 1, 2, 2, 3, 3, 3
auto it = ms.find(2); // 返回指向"第一個"2的迭代器
// 如果有多個相同元素,find返回中序遍歷遇到的第一個(3)erase
multiset::erase(key)會刪除所有匹配的鍵,返回刪除的總數。
std::multiset<int> ms = {1, 2, 2, 2, 3};
size_t n = ms.erase(2); // 刪除所有值為2的元素
// n = 3 (刪除了3個元素)
// ms 變為 {1, 3}(4)count
multiset::count返回元素的實際數量,而不僅僅是檢查是否存在。
std::multiset<int> ms = {1, 2, 2, 3, 3, 3};
size_t c = ms.count(2); // 返回元素的實際個數
// c = 2 (有兩個2)
size_t c2 = ms.count(3); // c2 = 3 (有三個3)(5)lower_bound / upper_bound
雖然函數原型相同,但在
multiset中的意義更豐富。
std::multiset<int> ms = {1, 2, 3, 3, 3, 4, 5};
auto low = ms.lower_bound(3); // 指向第一個 >=3 的元素 (第一個3)
auto up = ms.upper_bound(3); // 指向第一個 >3 的元素 (4)
// 可以用它們來遍歷所有3
for (auto it = low; it != up; ++it) {
std::cout << *it << " "; // 輸出: 3 3 3
}(6)equal_range - 相等範圍
std::set<int> s = {1, 2, 3, 4, 5};
auto range = s.equal_range(3);
// range.first 指向3
// range.second 指向4
// 範圍最多包含一個元素
std::multiset<int> ms = {1, 2, 3, 3, 3, 4, 5};
auto range = ms.equal_range(3);
// range.first 指向第一個3
// range.second 指向4
// [range.first, range.second) 包含所有3個"3"
for (auto it = range.first; it != range.second; ++it)
std::cout << *it << " "; // 輸出: 3 3 34. 練習
我真覺得這兩個沒啥好講的,學了set簡直是降為打擊
(1)兩個數組的交集
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2)
{
vector<int> ret;
set<int> s1(nums1.begin(),nums1.end());
set<int> s2(nums2.begin(),nums2.end());
for(auto e:s1)
{
if(s2.find(e)!=s2.end()) ret.push_back(e);
}
return ret;
}
};
//也能用雙指針(2)環形鏈表II
class Solution {
public:
ListNode *detectCycle(ListNode *head)
{
ListNode *cur=head;
set<ListNode *> s;
while(cur)
{
auto p = s.insert(cur);
if(!p.second) return cur;
cur=cur->next;
}
return cur;
}
};四、map / multimap 的使用
1. map 與 multimap的介紹
map的聲明如上圖,Key就是map底層關鍵字的類型,T是map底層value的類型,map默認要求Key支持小於比較,如果不支持或者需要的話可以自行實現仿函數傳給第二個模版參數,map底層存儲數據的內存是從空間配置器申請的。一般情況下,我們都不需要傳後兩個模版參數。map底層是用紅黑樹實現,增刪查改效率是O(logN),迭代器遍歷是走的中序,所以是按key有序順序遍歷的。map底層的紅黑樹節點中的數據,使用pair<Key,T>存儲鍵值對數據。用一句話總結它們的作用就是像一個有序的字典,根據Key查找T,map裏的Key沒有重複值,而multiset裏的Key可以有重複值。兩個字就是“映射”。
2. map的成員函數
其實和set大差不差,只是多了一個Value值。
(1)構造與迭代器
void test4()
{
// 1. 默認構造
std::map<std::string, int> m1;
// 2. 迭代器範圍構造 (迭代器必須指向pair對象)
std::vector<pair<string, int>> v = { {"apple", 1}, {"banana", 2} };
std::map<string, int> m2(v.begin(), v.end());
// 3. 拷貝構造
std::map<string, int> m3(m2);
// 4. 初始化列表構造 (C++11)
std::map<string, int> m4{ { "apple", 1 }, { "banana", 2 }, { "cherry", 3 } };
//千萬不能寫成 ({},{},..)
//std::map<std::string, int> m4 = { {"apple", 1}, {"banana", 2}, {"cherry", 3} };
std::map<std::string, int> m = { {"apple", 1}, {"banana", 2}, {"cherry", 3} };
// 正向迭代器 (按鍵排序: apple, banana, cherry)
for (auto it = m.begin(); it != m.end(); ++it) {
std::cout << it->first << ": " << it->second << std::endl;
// it->first 是 const,不能修改
// it->second 可以修改
}
for (const auto& kv : m) {
std::cout << kv.first << ": " << kv.second << std::endl;
}
// 反向迭代器 (cherry, banana, apple)
for (auto rit = m.rbegin(); rit != m.rend(); ++rit) {
std::cout << rit->first << ": " << rit->second << std::endl;
}
}(2)增刪查
pair<iterator,bool> insert (const value_type& val);
返回值是pair,而pair的first是迭代器,指向map存儲的另一個pair。
void test5()
{
map<string, int> m;
// 1. 插入單個pair,返回 pair<iterator, bool>
auto ret = m.insert({ "apple", 1 });
// ret.second 為true表示插入成功,false表示key已存在
// 2. 插入迭代器範圍
vector<pair<std::string, int>> v = { {"date", 4}, {"elderberry", 5} };
m.insert(v.begin(), v.end());
// 3. 使用初始化列表
m.insert({ {"fig", 6}, {"grape", 7} });
auto it = m.find("b");
// 1. 通過迭代器位置刪除
if (it != m.end())
m.erase(it); // 刪除 "b"
// 2. 通過key刪除,返回刪除的元素個數 (0或1)
size_t count = m.erase("c");
// 3. 刪除迭代器範圍
m.erase(m.begin(), m.begin()++); // 刪除前兩個元素
cout << m.size();
m.clear();
cout << endl << m.empty() << endl;
}(3)operator[ ]
先看一下operator[ ]的底層實現
mapped_type& operator[] (const key_type& k)
{
pair<iterator, bool> ret = insert({ k, mapped_type() });
iterator it = ret.first;
return it->second;
}
- 如果k不在map中,insert會插入k和mapped_type默認值,同時[]返回結點中存儲mapped_type值的引用,那麼我們可以通過引用修改映射值。所以[]具備了插入+修改功能。
- 如果k在map中,insert會插入失敗,但是insert返回pair對象的first是指向key結點的迭代器,返回值同時[]返回結點中存儲mapped_type值的引用,所以[]具備了查找+修改的功能。
void test6()
{
map<string, int> m;
// 1. 插入新元素 (key不存在時)
m["apple"] = 5; // 插入 {"apple", 5}
// 2. 修改現有元素 (key存在時)
m["apple"] = 10; // 修改為 {"apple", 10}
// 3. 查找/訪問元素
std::cout << m["apple"] << std::endl; // 輸出: 10
// 4. 注意:如果key不存在,operator[]會插入該key,並用默認值初始化value
std::cout << m["banana"] << std::endl; // 自動插入 {"banana", 0}
}(4)其他成員函數
void test7()
{
map<string, int> m1 = { {"apple", 1} };
if (m1.count("apple") == 1)
cout << "Key exists" << endl;
map<string, int> m2 = { {"apple", 1}, {"banana", 2}, {"cherry", 3} };
auto it1 = m2.lower_bound("b");
// it1 指向 "banana" (第一個 >= "b" 的元素)
map<string, int> m3 = { {"apple", 1}, {"banana", 2}, {"cherry", 3} };
auto it2 = m3.upper_bound("b");
// it2 指向 "cherry" (第一個 > "b" 的元素)
}
3. multimap 的不同特徵
multimap和map的使用基本完全類似,主要區別點在於multimap支持關鍵值key冗餘,那麼insert/find/count/erase都圍繞着支持關鍵值key冗餘有所差異,這裏跟set和multiset完全一樣,比如find時,有多個key,返回中序第一個。其次,就是multimap不支持[],因為支持key冗餘,[]就只能支持插入了,不能支持修改。舉一個例子:
std::map<std::string, int> m = {{"apple", 1}, {"banana", 2}};
auto range = m.equal_range("apple");
// range包含最多一個元素
std::multimap<std::string, int> mm = {
{"apple", 1}, {"apple", 2}, {"apple", 3}, {"banana", 4}
};
auto range = mm.equal_range("apple");
// range.first 指向第一個apple
// range.second 指向banana (第一個不是apple的元素)
// 遍歷所有"apple"
for (auto it = range.first; it != range.second; ++it) {
std::cout << it->first << ": " << it->second << std::endl;
}
// 輸出:
// apple: 1
// apple: 2
// apple: 34. 練習
複製帶隨機指針的鏈表
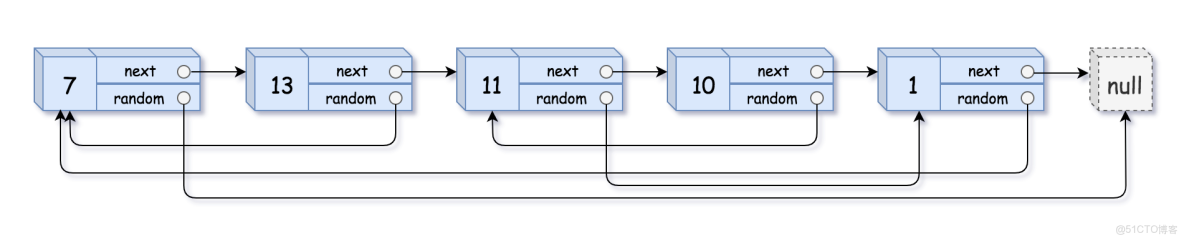
給你一個長度為 n 的鏈表,每個節點包含一個額外增加的隨機指針 random ,該指針可以指向鏈表中的任何節點或空節點。構造這個鏈表的深拷貝。 深拷貝應該正好由 n 個全新節點組成,其中每個新節點的值都設為其對應的原節點的值。新節點的 next 指針和 random 指針也都應指向複製鏈表中的新節點,並使原鏈表和複製鏈表中的這些指針能夠表示相同的鏈表狀態。複製鏈表中的指針都不應指向原鏈表中的節點 。例如,如果原鏈表中有 X 和 Y 兩個節點,其中 X.random --> Y 。那麼在複製鏈表中對應的兩個節點 x 和 y ,同樣有 x.random --> y 。返回複製鏈表的頭節點。
輸入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
輸出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
核心思路:難點就是要每次找到這個點的隨機指針指向哪,至於數據和next指針,那按照順序一個一個新建結點,順序連接就行了。那如果我們能把每個拷貝的結點與原結點對應起來,就是我説到拷貝結點,就一下子知道原結點在哪裏,那就好辦了,直接把拷貝結點的隨機指針指向從該拷貝結點找到的原結點的隨機指針對應的另一個拷貝結點。
解法一:那不就是映射嗎,這就是map的作用啊,key是原結點,value是對應相同的拷貝結點,copy->random = nodeMap[cur->random];
Node* copyRandomList1(Node* head)
{
map<Node*, Node*> m1;
Node* cur = head;
while (cur)
{
Node* copy = new Node(cur->val);
m1.insert({ cur,copy });
cur = cur->next;
}
cur = head;
while (cur)
{
m1[cur]->next = m1[cur->next];
m1[cur]->random = m1[cur->random];
cur = cur->next;
}
return m1[head];
}解法二:將新舊鏈表混合,把原結點的next改成它的拷貝結點,這樣,當我説到拷貝結點,那它的原結點就是它的上一個。最後剝離出來就行。
// 使用鏈表交錯方法的深拷貝
Node* copyRandomList2(Node* head)
{
if (!head) return nullptr;
// 第一步:在每個原節點後面插入對應的拷貝節點
// 創建交錯鏈表:原節點1 -> 拷貝節點1 -> 原節點2 -> 拷貝節點2 -> ...
Node* cur = head;
while (cur)
{
// 創建當前節點的拷貝節點
Node* copy = new Node(cur->val);
// 將拷貝節點插入到原節點後面
copy->next = cur->next;
cur->next = copy;
// 移動到下一個原節點(跳過剛插入的拷貝節點)
cur = cur->next->next;
}
// 第二步:設置拷貝節點的random指針
// 利用交錯結構:拷貝節點的random = 原節點random的next
cur = head;
while (cur)
{
// 如果原節點有random指針,設置對應拷貝節點的random指針
if (cur->random)
// cur->random->next 指向對應的拷貝節點
cur->next->random = cur->random->next;
// 移動到下一個原節點(跳過拷貝節點)
cur = cur->next->next;
}
// 第三步:分離原鏈表和拷貝鏈表
Node* ret = head->next; // 拷貝鏈表的頭節點
Node* newcur = ret; // 拷貝鏈表的當前節點
cur = head; // 原鏈表的當前節點
while (cur)
{
// 恢復原鏈表的next指針:跳過拷貝節點,指向下一個原節點
cur->next = cur->next->next;
// 連接拷貝鏈表的next指針:指向下一個拷貝節點
if (newcur->next)
newcur->next = newcur->next->next;
// 移動到下一組節點
cur = cur->next; // 移動到原鏈表的下一個原節點
newcur = newcur->next; // 移動到拷貝鏈表的下一個拷貝節點
}
return ret;
}五、unordered_(multi)set 與 unordered_(multi)map 的使用
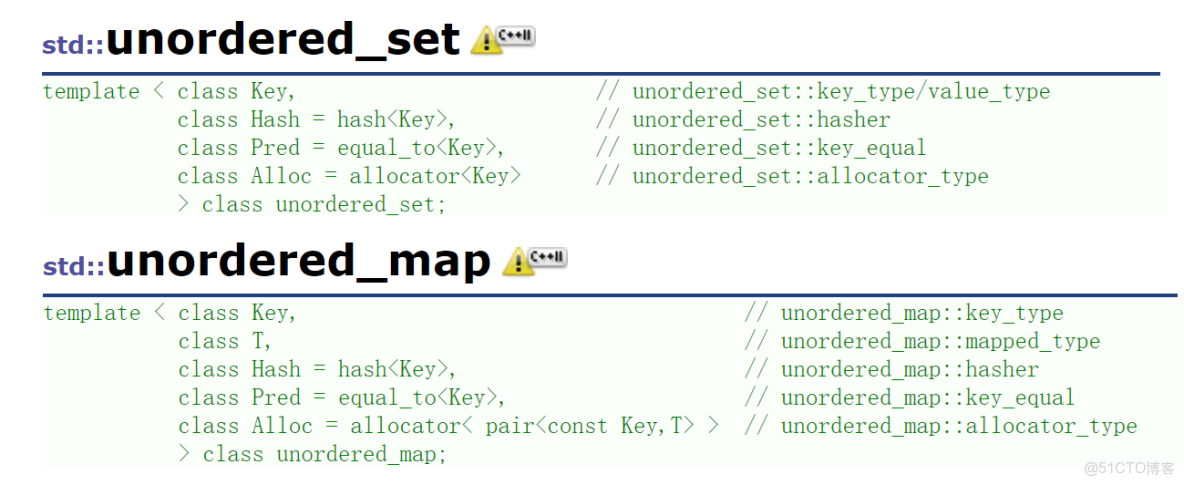
1. 容器介紹
看這個之前一定要學會哈希桶,沒加multi表示key不能重複,加multi表示key能重複,這些參數是什麼意思,在上一篇博客中都講過。unordered_(multi)set 與 unordered_(multi)map的底層是哈希桶,這是和前面幾個容器最大的區別。它查找、插入和刪除操作的時間複雜度都是O(1)。
2. 和(multi)set、(multi)map的區別
(1)(multi)set、(multi)map有的成員函數unordered_(multi)set 與 unordered_(multi)map都有,且用法一模一樣,但是unordered_(multi)set 和 unordered_(multi)map 是無序的!
(2)對Key的要求不同,(multi)set、(multi)map要求Key支持小於比較,而unordered_***要求Key支持轉成整形且支持等於比較。
(3)unordered_(multi)set 與 unordered_(multi)map的迭代器是單項迭代器,只支持++(在我們實現哈希桶時,只有next指針)
(4)unordered***的增刪查改更快一些,因為紅黑樹增刪查改效率是O(logN),而哈希表增刪查平均效率是O(1)。
3. 增加的成員函數
增加的都是有關哈希的函數
void test8()
{
unordered_set<int> us = { 1, 2, 3, 4, 5, 10, 15 };
//bucket_count() - 返回桶的數量
cout << "桶的數量: " << us.bucket_count() << endl;
// bucket_size(n) - 返回指定桶中的元素數量
for (size_t i = 0; i < us.bucket_count(); ++i)
cout << "桶 " << i << " 有 " << us.bucket_size(i) << " 個元素" << endl;
//bucket - 查找元素所在的桶索引
for (int value : us)
{
size_t bucket_idx = us.bucket(value);
cout << "元素 " << value << " 在桶 " << bucket_idx << endl;
}
//load_factor - 返回負載因子 負載因子 = 元素數量 / 桶數量
cout << "負載因子: " << us.load_factor() << endl;
//rehash - 直接設置桶的數量
us.rehash(20);
cout << us.bucket_count() << endl;
//reserve - 預留容量(一般用這個)
us.reserve(1000); // 預期要插入1000個元素,提前預留空間
std::cout << "預留後桶數量: " << us.bucket_count() << endl;
//它們都會略大於給的數據
}4. 練習
前K個高頻單詞
核心思路:一看就是用map統計單次數量(要是這沒看出來,那這篇白學了),重要的是我怎麼按照他的要求排序,數字是降序,字符串是升序,他倆還在一個pair裏,這百分百要寫仿函數了。
仿函數怎麼看升序降序?
class a //升序{ public: bool operator()(int x, int y) { return x < y; } }; class b //降序 { public: bool operator()(int x, int y) { return x > y; } }; class c //降序 { public: bool operator()(int x, int y) { return y < x; } }; class d //升序 { public: bool operator()(int x, int y) { return y > x; } };
小妙招:把參數按順序換成具體數字,返回值如果為真,那就不動,為假,就交換。例如c,設x=5,y=7,順序是5->7,返回有7<5,為假,交換,7->5,所以為降序。
解法一:unordered_map + priority_queue(Top-K問題)
不用Top-K就按次數建大堆,取前十個;用Top-K就建小堆,堆裏的十個倒序輸出。(忘記的請複習“【二叉樹與堆】三.4”)
//沒用Top-K
struct Comp1
{
bool operator()(const pair<string, int>& p1, const pair<string, int>& p2)
{
if (p1.second != p2.second) return p1.second < p2.second;
else return p1.first > p2.first;
}
};
class Solution {
public:
vector<string> topKFrequent1(vector<string>& words, int k)
{
unordered_map<string, int> m;
for (auto e : words)
{
m[e]++;
}
vector<string> strV;
priority_queue<pair<string, int>, vector<pair<string, int>>, Comp1> pq;
for (auto it = m.begin(); it != m.end(); it++)
{
pq.push({ it->first,it->second });
}
for (int i = 0; i < k; ++i)
{
strV.push_back(pq.top().first);
pq.pop();
}
return strV;
}
};注意點:priority_queue中,大堆排的升序,小堆排的是降序!
解法二:unordered_map + sort
struct Comp2
{
bool operator()(const pair<string, int>& p1, const pair<string, int>& p2)
{
if (p1.second != p2.second) return p1.second > p2.second;
else return p1.first < p2.first;
}
};
vector<string> topKFrequent2(vector<string>& words, int k)
{
unordered_map<string, int> m;
for (auto e : words)
{
m[e]++;
}
vector<string> strV;
vector<pair<string, int>> v(m.begin(), m.end());
// 仿函數控制降序,仿函數控制次數相等,字典序小的在前面
sort(v.begin(), v.end(), Comp2());
// 取前k個
for (int i = 0; i < k; ++i)
{
strV.push_back(v[i].first);
}
return strV;
}解法三:map + stable_sort
這樣,map裏的自動排序就有了意義。
struct Comp3
{
bool operator()(const pair<string, int>& x, const pair<string, int>& y) const
{
return x.second > y.second;
}
};
vector<string> topKFrequent3(vector<string>& words, int k) {
map<string, int> countMap;
for (auto& e : words)
{
countMap[e]++;
}
vector<pair<string, int>> v(countMap.begin(), countMap.end());
// 仿函數控制降序
stable_sort(v.begin(), v.end(), Comp3());
// 取前k個
vector<string> strV;
for (int i = 0; i < k; ++i)
{
strV.push_back(v[i].first);
}
return strV;
}六、紅黑樹封裝 set 與 map
1. 泛型編程的應用
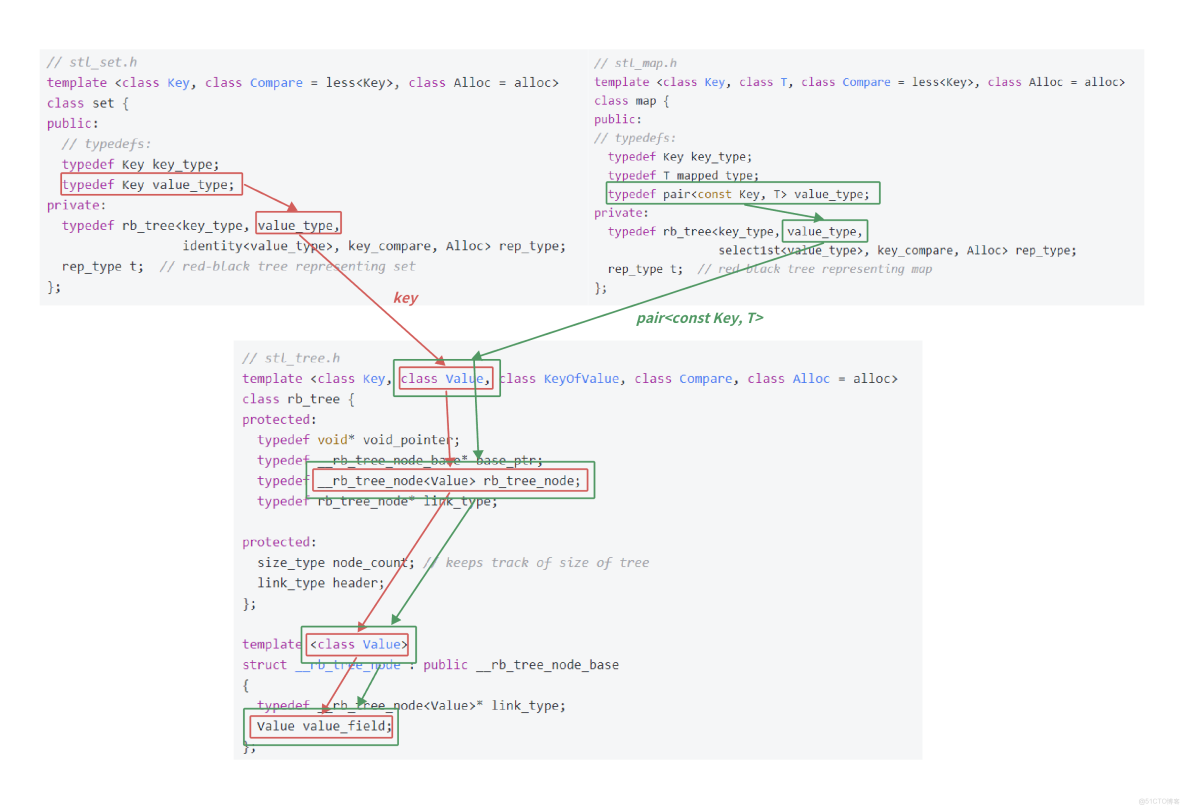
我們在之前用kv模型實現了紅黑樹,如果稍微改一改就可以改成map的實現,可是明明一樣的代碼,set寫一遍,map寫一遍,那我們學的泛型編程還有什麼意義呢?我們來看看源碼中怎麼做的。
通過上圖對框架的分析,我們可以看到源碼中rb_tree用了一個巧妙的泛型思想實現,rb_tree是實現key的搜索場景,還是key/value的搜索場景不是直接寫死的,而是由第二個模板參數Value決定_rb_tree_node中存儲的數據類型。
- set實例化rb_tree時第二個模板參數給的是key,map實例化rb_tree時第二個模板參數給的是pair<key, T>,這樣一顆紅黑樹既可以實現key搜索場景的set,也可以實現key/value搜索場景的map。
- 要注意一下,源碼裏面模板參數是用T代表value,而內部寫的value_type不是我們日常key/value場景中説的value,源碼中的value_type反而是紅黑樹結點中存儲的真實的數據的類型。我們下面實現時會統一的
- rb_tree第二個模板參數Value已經控制了紅黑樹結點中存儲的數據類型,為什麼還要傳第一個模板參數Key呢?尤其是set,兩個模板參數是一樣的,這是很多同學這時的一個疑問。要注意的是對於map和set,find/erase時的函數參數都是Key,所以第一個模板參數是傳給find/erase等函數做形參的類型的。對於set而言兩個參數是一樣的,但是對於map而言就完全不一樣了,map insert的是pair對象,但是find和ease的是Key對象。
- 因為RBTree實現了泛型不知道T參數到底是K,還是pair<K, V>,那麼insert內部進行插入邏輯比較時,就沒辦法進行比較,因為pair的默認支持的是key和value一起參與比較,我們需要的是任何時候只比較key,所以我們在map和set層分別實現一個MapOfT和SetOfT的仿函數傳給RBTree的KeyOfT,然後RBTree中通過KeyOfT仿函數取出T類型對象中的key,再進行比較。
enum Colour
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
T _data;
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
Colour _col; //節點顏色
RBTreeNode(const T& data)
:_data(data),
_parent(nullptr),
_left(nullptr),
_right(nullptr)
{ }
};
template<class K, class T, class KeyOfT>
class RBTree
{
public:
typedef RBTreeNode<T> Node;
private:
Node* _root = nullptr;
};
template<class K>
class set
{
struct SetOfK
{
const K& operator()(const K& date)
{
return date;
}
};
RBTree<K, const K, SetOfK> _t;
};
template<class K, class V>
class map
{
struct MapOfK
{
const K& operator()(const pair<K, V>& date)
{
return date.first;
}
};
private:
RBTree<K, pair<const K, V>, MapOfK> _t;
};這樣的話,代碼的簡潔性與可讀性就十分的強了。
但是我説白了,我白説了,看到這裏,有人會説,我直接寫template<class K, class V> RBTree,在set裏傳set<K,K>不行嗎,這都不用實現KeyOfT!其實你改改是可以的,但是你的可讀性就大大降低了,我們不選擇這樣實現。(沒看懂這句話的往下看就行了,不用懂)
2. iterator的實現
(1)細節處理
1> iterator實現的大框架跟list的iterator思路是一致的,用一個類型封裝結點的指針,再通過重載運算符實現,迭代器像指針一樣訪問的行為。
2> set的iterator也不支持修改,我們把set的第二個模板參數改成const K即可,RBTree<K, const K, SetKeyOfT> _t; 那這樣其實set的const與非const沒什麼區別。
3> map的iterator不支持修改key但是可以修改value,我們把map的第二個模板參數pair的第一個參數改成const K即可,RBTree<K, pair<const K, V>, MapKeyOfT> _t;
4>
後綴都加const這樣保證了const對象只能調用const迭代器。(具體看實現)
(2)operator++() 與 operator--() 的實現
(以++為例,--與他恰好相反)
情況1:當前節點有右子樹
進入右子樹,一直向左走到底,找到的就是中序遍歷的下一個節點
原因:
- 中序遍歷順序:左子樹 → 根節點 → 右子樹
- 當前節點處理完後,下一個應該是右子樹中的最小節點
- 右子樹的最小節點就是一直向左走到底的節點
情況2:當前節點沒有右子樹
向上回溯,找到第一個"作為左孩子的祖先",該祖先節點就是下一個節點
原因:
- 如果沒有右子樹,説明當前子樹已遍歷完
- 需要回到"尚未處理右子樹"的祖先節點
- 這個祖先就是第一個"當前節點在其左子樹中"的節點
Self& operator++()
{
assert(_node != nullptr);
if (_node->_right)
{
_node = _node->_right;
while (_node->_left)
{
_node = _node->_left;
}
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node->_left)
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}情況3:end()--
這也是我們為什麼要傳root,end() 指向 nullptr,我們需要找到中序遍歷的最後一個元素,而最後一個元素就是整棵樹的最右節點,我們只有從根開始,遍歷到最右節點。
if (_node == nullptr) // --end()
{
// --end(),特殊處理,走到中序最後一個結點,整棵樹的最右結點
Node* rightMost = _root;
while (rightMost && rightMost->_right)
{
rightMost = rightMost->_right;
}
_node = rightMost;
}stl庫裏的處理方式
STL的紅黑樹實現中有一個特殊的header節點,這個節點不存儲實際數據,但維護着關鍵指針:header->_parent 指向根節點;header->_left 指向最小節點(即begin());header->_right 指向最大節點(用於end()--)。end()--直接返回header->_right。但是它在插入時就比較麻煩了,它時刻要判斷這三個指針是否正確,各有各的劣勢吧。
3. insert的實現
我主要説一下改動的地方,下面所有函數改動邏輯是相同的,我以insert為例。
(1)返回參數修改為了pair<Iterator, bool>,注意返回值的方式。
(2)取關鍵字Key需要用仿函數
(3)operator[] 和前面的實現方法一樣
pair<Iterator, bool> Insert(const T& data)
{
KeyOfT kot;
Iterator it = Find(kot(data));
if (it != End())
return { it, false };
if (load_factor() > 0.98)
{
vector<Node*> newtables;
newtables.resize(__stl_next_prime(_tables.size() + 1));
Hash hash;
for (int i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(kot(cur->_data)) % newtables.size();
cur->_next = newtables[hashi];
newtables[hashi] = cur;
cur = next;
}
}
_tables.swap(newtables);
}
Hash hash;
size_t hashi = hash(kot(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[hashi];
_tables[hashi] = newnode;
_n++;
return { Iterator(newnode, this), true };
}4. 完整代碼
//RBTree.h
#pragma once
#include<iostream>
#include <utility>
#include<math.h>
#include<assert.h>
using namespace std;
enum Colour
{
RED,
BLACK
};
template<class T>
struct RBTreeNode
{
T _data;
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
Colour _col; //節點顏色
RBTreeNode(const T& data)
:_data(data),
_parent(nullptr),
_left(nullptr),
_right(nullptr)
{ }
};
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T, Ref, Ptr> Self;
Node* _node;
Node* _root;
RBTreeIterator(Node* node, Node* root)
:_node(node)
, _root(root)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(_node->_data);
}
Self& operator++()
{
assert(_node != nullptr);
if (_node->_right)
{
_node = _node->_right;
while (_node->_left)
{
_node = _node->_left;
}
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator--()
{
if (_node == nullptr) // --end()
{
// --end(),特殊處理,走到中序最後一個結點,整棵樹的最右結點
Node* rightMost = _root;
while (rightMost && rightMost->_right)
{
rightMost = rightMost->_right;
}
_node = rightMost;
}
else if (_node->_left)
{
_node = _node->_left;
while (_node->_right)
{
_node = _node->_right;
}
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_left == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
bool operator!= (const Self& s) const
{
return _node != s._node;
}
bool operator== (const Self& s) const
{
return _node == s._node;
}
};
template<class K, class T, class KeyOfT>
class RBTree
{
public:
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T, T&, T*> Iterator;
typedef RBTreeIterator<T, const T&, const T*> ConstIterator;
Iterator Begin()
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return Iterator(cur, _root);
}
Iterator End()
{
return Iterator(nullptr, _root);
}
ConstIterator CBegin() const
{
Node* cur = _root;
while (cur && cur->_left)
{
cur = cur->_left;
}
return Iterator(cur, _root);
}
ConstIterator CEnd() const
{
return Iterator(nullptr, _root);
}
pair<Iterator, bool> insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return { Iterator(_root, _root), true };
}
KeyOfT kot;
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
parent = cur;
cur = cur->_right;
}
else
return { Iterator(cur, _root), false };
}
cur = new Node(data);
Node* newnode = cur;
if (kot(parent->_data) < kot(data))
{
parent->_right = newnode;
}
else
{
parent->_left = newnode;
}
newnode->_parent = parent;
newnode->_col = RED;
while (parent && cur->_col == RED)
{
if (cur->_parent && cur->_parent->_col == BLACK) break;
Node* grandparent = parent->_parent;
//parent不為根節點,grandparent一定存在
if (grandparent->_left == parent)
{
Node* uncle = grandparent->_right;
{
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandparent->_col = RED;
cur = grandparent;
parent = cur->_parent;
}
else
{
if (parent->_left == cur)
{
RotateR(grandparent);
grandparent->_col = RED;
parent->_col = BLACK;
cur = parent;
}
else
{
RotateL(parent);
RotateR(grandparent);
cur->_col = BLACK;
grandparent->_col = RED;
}
}
}
}
// g
// u p
else if (grandparent->_right == parent)
{
Node* uncle = grandparent->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandparent->_col = RED;
cur = grandparent;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
RotateL(grandparent);
grandparent->_col = RED;
parent->_col = BLACK;
cur = parent;
parent = cur->_parent;
}
else
{
RotateR(parent);
RotateL(grandparent);
cur->_col = BLACK;
grandparent->_col = RED;
parent = cur->_parent;
}
}
}
else assert(false);
}
_root->_col = BLACK;
return { Iterator(newnode, _root), true };
}
Iterator Find(const K& key)
{
Node* cur = _root;
KeyOfT kot;
while (cur)
{
if (kot(cur->_data) < key)
{
cur = cur->_right;
}
else if (kot(cur->_data) > key)
{
cur = cur->_left;
}
else
{
return Iterator(cur, _root);
}
}
return Iterator(nullptr, _root);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
int Height()
{
return _Height(_root);
}
int Size()
{
return _Size(_root);
}
private:
Node* _root = nullptr;
//右單旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* grandparent = parent->_parent;
parent->_parent = subL;
parent->_left = subLR;
if (subLR) subLR->_parent = parent;
subL->_right = parent;
if (grandparent == nullptr)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parent == grandparent->_left)
grandparent->_left = subL;
else grandparent->_right = subL;
subL->_parent = grandparent;
}
}
//左單旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* grandparent = parent->_parent;
parent->_parent = subR;
parent->_right = subRL;
if (subRL) subRL->_parent = parent;
subR->_left = parent;
if (grandparent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == grandparent->_left)
grandparent->_left = subR;
else grandparent->_right = subR;
subR->_parent = grandparent;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
int _Size(Node* root)
{
if (root == nullptr)
return 0;
int a = _Size(root->_left);
int b = _Size(root->_right);
return a + b + 1;
}
};
//set.h
#pragma once
#include"RBTree.h"
namespace DaYuanTongXue
{
template<class K>
class set
{
struct SetOfK
{
const K& operator()(const K& date)
{
return date;
}
};
public:
typedef typename RBTree<K, const K, SetOfK>::Iterator iterator;
typedef typename RBTree<K, const K, SetOfK>::ConstIterator const_iterator;
iterator begin()
{
return _t.Begin();
}
iterator end()
{
return _t.End();
}
const_iterator cbegin() const
{
return _t.CBegin();
}
const_iterator cend() const
{
return _t.CEnd();
}
pair<iterator, bool> insert(const K& date)
{
return _t.insert(date);
}
iterator find(const K& date)
{
return _t.Find(date);
}
private:
RBTree<K, const K, SetOfK> _t;
};
}
//map.h
#pragma once
#include"RBTree.h"
namespace DaYuanTongXue
{
template<class K, class V>
class map
{
struct MapOfK
{
const K& operator()(const pair<K, V>& date)
{
return date.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, MapOfK>::Iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapOfK>::ConstIterator const_iterator;
iterator begin()
{
return _t.Begin();
}
iterator end()
{
return _t.End();
}
const_iterator cbegin() const
{
return _t.CBegin();
}
const_iterator cend() const
{
return _t.CEnd();
}
pair<iterator, bool> insert(const pair<K, V>& date)
{
return _t.insert(date);
}
iterator find(const K& date)
{
return _t.Find(date);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = _t.insert({ key, V() });
return ret.first->second;
}
private:
RBTree<K, pair<const K, V>, MapOfK> _t;
};
}七、哈希表封裝 unordered_set 與 unordered_map
1. 整體概述
結構上hash_map和hash_set跟map和set的完全類似,複用同⼀個hashtable實現key和key/value結構,hash_set傳給hash_table的是兩個key,hash_map傳給hash_table的是pair<const key, value>。相比於map和set,多了兩個模板參數class Hash, class Pred,要時刻記得把它們帶上。(這個的前後關聯更強,一定一定要對哈希桶的實現非常熟悉,要不然看的看的就懵了,這一塊主要還是得自己體會,泛型編程是非常重要的)
2. iterator的實現
(1)operator++() 的實現
- 噹噹前迭代器指向的節點在某個桶的鏈表中,且該節點還有下一個節點時,直接移動到鏈表中的下一個節點,這是最簡單最快的情況
- 噹噹前迭代器指向某個桶的鏈表最後一個節點時:
1> 計算下一個桶的索引:當前桶索引 + 1
2> 尋找非空桶:從下一個桶開始,逐個檢查每個桶,並跳過所有為空的桶(沒有鏈表的桶)
3> 定位到新鏈表的頭部:找到第一個非空桶,將迭代器指向該桶的鏈表頭節點
- 特殊邊界情況
1> 已經是最後一個元素:當遍歷到最後一個桶的最後一個節點時,operator++() 會將迭代器設置為 end()
2> 空容器:直接返回 end()
typedef HSIterator<K, T, Ref, Ptr, KeyOfT, Hash, Pred> Self;
Self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
KeyOfT kot;
Hash hash;
size_t hashi = hash(kot(_node->_data)) % _ht->_tables.size();
hashi++;
while (hashi < _ht->_tables.size())
{
if (_ht->_tables[hashi])
{
_node = _ht->_tables[hashi];
break;
}
else hashi++;
}
if (hashi == _ht->_tables.size())
_node = nullptr;
return *this;
}
}(2)外部類對Hashtable類的使用
我們在實現迭代器時,一定會訪問到Hashtable中的_table,我們有兩種傳參方式,一種是直接傳Hashtable._table,一種是直接傳一個類,其實前面那種是更方便的,但是它無法調用類中的其他東西,為了我們學習,選擇後者實現。
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Pred>
struct HSIterator
{
typedef HashNode<T> Node;
typedef Hashtable<K, T, KeyOfT, Hash, Pred> HT;
typedef HSIterator<K, T, Ref, Ptr, KeyOfT, Hash, Pred> Self;
Node* _node;
const HT* _ht;
HSIterator(Node* node, const HT* ht)
:_node(node)
,_ht(ht)
{}
};1> 迭代器一般在主類的前邊實現,當我們 typedef Hashtable<K, T, KeyOfT, Hash, Pred> HT; 編譯器會找不到Hashtable類,因為它不會往下找,所以需要前置聲明。
template<class K, class T, class KeyOfT, class Hash, class Pred> class Hashtable;
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Pred>
struct HSIterator
{
typedef HashNode<T> Node;
typedef Hashtable<K, T, KeyOfT, Hash, Pred> HT;
typedef HSIterator<K, T, Ref, Ptr, KeyOfT, Hash, Pred> Self;
//......
};2> 迭代器中要訪問Hashtable類的私有成員變量,所以要在主類中吧迭代器類設為友元。注意類模板聲明友元的方法。
template<class K, class T, class KeyOfT, class Hash, class Pred>
class Hashtable
{
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Pred>
friend struct HSIterator;
public:
typedef HashNode<T> Node;
typedef HSIterator<K, T, T&, T*, KeyOfT, Hash, Pred> Iterator;
typedef HSIterator<K, T, const T&, const T*, KeyOfT, Hash, Pred> ConstIterator;
//......
};3> template<......,class KeyOfT,class Hash, class Pred> struct HSIterator; Hash參數和 KeyOfT 參數用於++時重新算哈希值,以及用於實例化Hashtable類;Pred 只用於實例化Hashtable類。所以,如果你直接傳Hashtable._table,你寫Pred就沒用;如果你傳Hashtable._table,還傳了_bucketIndex(表示當前是哪個桶),那你只用寫成 template<class T, class Ref, class Ptr> 。
3. 完整代碼
//HSTable.h
#pragma once
#include<string>
#include<vector>
using namespace std;
template<class K>
struct myhash
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
template<>
struct myhash<std::string>
{
size_t operator()(const std::string& s)
{
size_t hash = 0;
for (auto ch : s)
{
hash += ch;
hash *= 131;
}
return hash;
}
};
template<class K>
struct myequal_to
{
bool operator()(const K& lhs, const K& rhs) const
{
return lhs == rhs;
}
};
template<class T>
struct HashNode
{
T _data;
HashNode* _next;
HashNode(const T& data)
:_data(data),
_next(nullptr)
{ }
};
template<class K, class T, class KeyOfT, class Hash, class Pred>
class Hashtable;
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Pred>
struct HSIterator
{
typedef HashNode<T> Node;
typedef Hashtable<K, T, KeyOfT, Hash, Pred> HT;
typedef HSIterator<K, T, Ref, Ptr, KeyOfT, Hash, Pred> Self;
Node* _node;
const HT* _ht;
HSIterator(Node* node, const HT* ht)
:_node(node)
,_ht(ht)
{}
Ptr operator->()
{
return &(_node->_data);
}
Ref operator*()
{
return _node->_data;
}
bool operator!=(const Self& it)
{
return _node != it._node;
}
bool operator==(const Self& it)
{
return _node == it._node;
}
Self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
KeyOfT kot;
Hash hash;
size_t hashi = hash(kot(_node->_data)) % _ht->_tables.size();
hashi++;
while (hashi < _ht->_tables.size())
{
if (_ht->_tables[hashi])
{
_node = _ht->_tables[hashi];
break;
}
else hashi++;
}
if (hashi == _ht->_tables.size())
_node = nullptr;
return *this;
}
}
};
template<class K, class T, class KeyOfT, class Hash, class Pred>
class Hashtable
{
template<class K, class T, class Ref, class Ptr, class KeyOfT, class Hash, class Pred>
friend struct HSIterator;
public:
typedef HashNode<T> Node;
typedef HSIterator<K, T, T&, T*, KeyOfT, Hash, Pred> Iterator;
typedef HSIterator<K, T, const T&, const T*, KeyOfT, Hash, Pred> ConstIterator;
inline unsigned long __stl_next_prime(unsigned long n)
{
static const int __stl_num_primes = 28;
static const unsigned long __stl_prime_list[__stl_num_primes] = {
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
const unsigned long* first = __stl_prime_list;
const unsigned long* last = __stl_prime_list + __stl_num_primes;
const unsigned long* pos = lower_bound(first, last, n);
return pos == last ? *(last - 1) : *pos;
}
Hashtable()
:_tables(__stl_next_prime(0))
, _n(0)
{}
~Hashtable()
{
for (int i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}
Iterator Begin()
{
for (int i = 0; i < _tables.size(); i++)
{
if (_tables[i]) return Iterator(_tables[i], this);
}
return End();
}
Iterator End()
{
return Iterator(nullptr, this);
}
ConstIterator cEnd() const
{
return ConstIterator(nullptr, this);
}
ConstIterator cBegin() const
{
for (int i = 0; i < _tables.size(); i++)
{
if (_tables[i]) return ConstIterator(_tables[i], this);
}
return cEnd();
}
float load_factor() const
{
return (float)_n / (float)(_tables.size());
}
pair<Iterator, bool> Insert(const T& data)
{
KeyOfT kot;
Iterator it = Find(kot(data));
if (it != End())
return { it, false };
if (load_factor() > 0.98)
{
vector<Node*> newtables;
newtables.resize(__stl_next_prime(_tables.size() + 1));
Hash hash;
for (int i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(kot(cur->_data)) % newtables.size();
cur->_next = newtables[hashi];
newtables[hashi] = cur;
cur = next;
}
}
_tables.swap(newtables);
}
Hash hash;
size_t hashi = hash(kot(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[hashi];
_tables[hashi] = newnode;
return { Iterator(newnode, this), true };
}
Iterator Find(const K& key)
{
KeyOfT kot;
Hash hash;
Pred equal;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (equal(kot(cur->_data), key))
return Iterator(cur, this);
else cur = cur->_next;
}
return End();
}
bool Erase(const K& key)
{
KeyOfT kot;
Hash hash;
Pred equal;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
Node* prev = nullptr;
while (cur)
{
if (equal(kot(cur->_data), key))
{
if (prev == nullptr)
_tables[hashi] = cur->_next;
else
prev->_next = cur->_next;
delete cur;
_n--;
return true;
}
else
{
prev = cur;
cur = cur->_next;
}
}
return false;
}
private:
std::vector<Node*> _tables;
size_t _n;
};
//unordered_set.h
#pragma once
#include"HSTable.h"
using namespace std;
template<class K, class Hash = myhash<K>, class Pred = myequal_to<K>>
class myunordered_set
{
public:
struct SetOfT
{
const K& operator()(const K& key)
{
return key;
}
};
typedef typename Hashtable<K, const K, SetOfT, Hash, Pred>::Iterator iterator;
typedef typename Hashtable<K, const K, SetOfT, Hash, Pred>::ConstIterator const_iterator;
iterator begin()
{
return _ht.Begin();
}
iterator end()
{
return _ht.End();
}
const_iterator cbegin() const
{
return _ht.cBegin();
}
const_iterator cend() const
{
return _ht.cEnd();
}
pair<iterator, bool> insert(const K& key)
{
return _ht.Insert(key);
}
iterator find(const K& key)
{
return _ht.Find(key);
}
bool erase(const K& key)
{
return _ht.Erase(key);
}
private:
Hashtable<K, const K, SetOfT, Hash, Pred> _ht;
};
//unordered_map.h
#pragma once
#include"HSTable.h"
using namespace std;
template<class K, class V, class Hash = myhash<K>, class Pred = myequal_to<K>>
class myunordered_map
{
public:
struct MapOfT
{
const K& operator()(const pair<K,V>& kv)
{
return kv.first;
}
};
typedef typename Hashtable<K, pair<const K, V>, MapOfT, Hash, Pred>::Iterator iterator;
typedef typename Hashtable<K, pair<const K, V>, MapOfT, Hash, Pred>::ConstIterator const_iterator;
iterator begin()
{
return _ht.Begin();
}
iterator end()
{
return _ht.End();
}
const_iterator cbegin() const
{
return _ht.cBegin();
}
const_iterator cend() const
{
return _ht.cEnd();
}
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _ht.Insert(kv);
}
iterator find(const K& key)
{
return _ht.Find(key);
}
bool erase(const K& key)
{
return _ht.Erase(key);
}
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert({ key, V() });
return ret.first->second;
}
private:
Hashtable<K, pair<const K, V>, MapOfT, Hash, Pred> _ht;
};