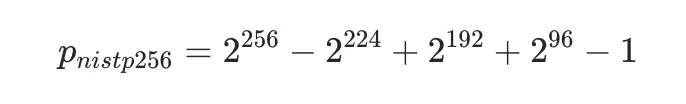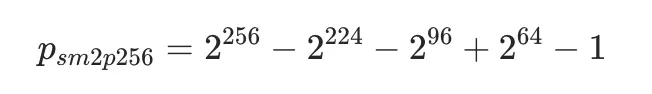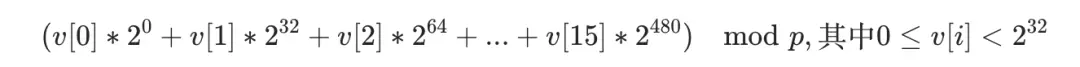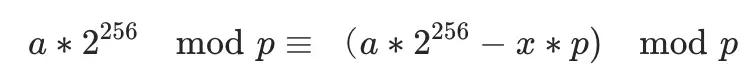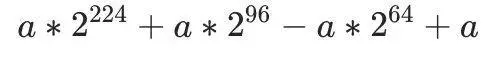本文是對 《銅鎖 SM2 算法性能優化實踐（一）｜綜述》 的深入擴展，詳細介紹快速模約減算法實現。
原文鏈接：https://www.yuque.com/tsdoc/ts/pacggl7s29yzsm19

背景

在 SM2 數字簽名算法中，有限域運算是橢圓曲線點運算和數字簽名運算的基礎，其運算性能將直接影響整體性能表現。而在有限域運算中，模約減運算的整體使用頻率最高，在模乘、模平方、模逆等運算中均有運用。以模乘法為例，其定義為：對於素數域參數 p 和乘數 a，模乘運算的結果等於 a*a mod p。也就是説，對於乘法結果大於 p 的中間值，模乘法需要將其約減到 p 以內，此過程因此被稱為模約減。

由於 p 是一個非常大的素數，且上述運算中間值最大可達 p2-1，採用除法來計算模約減的效率將極其低下 （ 在具體實踐中，有限域除法一般藉助乘法逆元實現，其耗時大約是模乘運算的 200-300 倍） 。目前，銅鎖項目中 SM2 算法使用了通用蒙哥馬利約分算法實現模約減過程，暫時沒有針對曲線特化的快速模約減算法實現。相應的，部分常用的 NIST 曲線 nistp224、nistp256 和 nistp521 基於廣域梅森素數實現了曲線特化的快速模約減算法，並運用於各自的 64-bit 平台優化中。

考慮到 SM2 曲線同樣採用廣域梅森素數作為素數域參數，且實現 64-bit 平台優化也需要使用模約減算法，因此為 SM2 曲線實現曲線參數特化的快速模約減算法是非常有必要的。同時，為了保證對部分 32 位平台的兼容性和後續擴展，在功能開發的過程中保留了原有的條件編譯模式，同時支持 32 位和 64 位平台使用該快速模約減算法。測試結果表明，使用了快速模約減的 SM2 模乘運算與簡單模乘和蒙哥馬利模乘相比，時間開銷分別降低 81.34% 和 29.91% 。

預備知識

在數論中，梅森素數 （Mersenne Prime) 是形如 2n-1 的質數，其中 n 為整數。梅森素數的數量非常稀少，直到今天 （2023 年 8 月） 僅有 51 個梅森素數被發現。由於梅森素數的構成與 2 的指數冪相關，在以二進制為數據表示方式的現代計算機中，它不僅便於計算和存儲，也能夠加速有限域運算，因此在密碼學領域廣受青睞。NIST 曲線家族中，nistp521 曲線的素數域參數 p 就選擇了梅森素數 2521-1。

然而，梅森素數的數量實在是過於稀少，以至於在橢圓曲線素數域參數 p 的合理取值範圍內僅有一個梅森素數 2521-1，其他的梅森素數要麼過大，要麼太小，不滿足使用要求。因此，許多橢圓曲線的素數域參數 p 選用了梅森素數的拓展版本——廣義梅森素數 （General Mersenne Prime) 。廣義梅森素數是形如 f(2n) 的素數，其中 f(x) 是具有較小整數係數的低次多項式。例如，nistp256 曲線採用如下所示的廣義梅森素數作為素數域參數 p：

算法原理

在國標 GM/T 0003.5-2012 中，給出了 SM2 曲線的推薦素數域參數 p。p 是一個廣義梅森素數，表示如下：

下面以大整數 v(v<p2<2512) 和參數 psm2p256 為例，推導基於廣義梅森素數的快速模約減算法。該算法利用參數 psm2p256 各項係數之間最小差為 232 的特點，將表示中間值的大整數按照 32 位分割，並轉化為如下表示形式：

然後將 v[8]-v[15] 的高位參數約化到 v[0]-v[7]  的低位參數上。在約化之前，我們先根據將參數 psm2p256 轉化為按照 32 位分割的表示形式：

接下來處理所有高位參數，此處以 v[8] 為例，設 v[8]=a，那麼 v[8] 可以表示為：

注意到，根據模運算的運算規則：

也就是説，在原數的基礎上增減模數 p 的倍數並不影響模運算的結果。那麼，為了消去高位參數 a，不妨減去一個 a*p，此時有：

上下相減，高位參數 v[8] 被成功消除，低位約化的結果為：

依次對 v[8]-v[15] 做低位約化即可消除所有高位參數。將所有的低位約化結果合併同類項，可得到如下的 SM2 快速模約減算法。該算法由白國強[1]等人於 2014 年首次提出，實際運用中也有多種不同的參數組合形式：

圖1：基於參數 psm2p256 的快速模約減算法

最後對約化後的低位參數 v[0]-v[7] 再做一次約減，旨在將模約減結果規約到 [0,p）範圍內。
此處最多需要減去 13p 即可得到最終結果，無需使用成本昂貴的模除法。從圖1中不難看出，基於廣義梅森素數的 SM2 快速模約減算法僅需要少量的有限域加法和減法即可實現，性能表現明顯優於使用模逆元的模約減算法。

算法實現

本節將介紹所實現算法的核心部分，完整算法實現請參見 crypto/bn/bn_sm2.c。

前文提到，在高位參數約化後，還需要對低位參數做約化以獲得最終結果，也就是減去參數 p 的某個倍數 np(0≤p≤13)。為了進一步提高性能，在代碼實現中我們構造一個預計算表以存儲 1-13p，以節約計算 np 的開銷。又因為約減結果在 【0,p) 範圍內，且

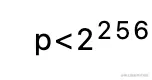
，因此只需要保留預計算參數的低 256 位：

/*
 * /* Pre-computed tables are "carry-less" values of modulus*(i+1),
 * all values are in little-endian format.
 */
static const BN_ULONG _sm2_p_256[][BN_SM2_256_TOP] = {
    {0xFFFFFFFFFFFFFFFFull, 0xFFFFFFFF00000000ull,
     0xFFFFFFFFFFFFFFFFull, 0xFFFFFFFEFFFFFFFFull},/*p*/
    {0xFFFFFFFFFFFFFFFEull, 0xFFFFFFFE00000001ull,
     0xFFFFFFFFFFFFFFFFull, 0xFFFFFFFDFFFFFFFFull},/*2p*/
    ...
    {0xFFFFFFFFFFFFFFF4ull, 0xFFFFFFF40000000Bull,
     0xFFFFFFFFFFFFFFFFull, 0xFFFFFFF3FFFFFFFFull},/*12p*/
    {0xFFFFFFFFFFFFFFF3ull, 0xFFFFFFF30000000Cull,
     0xFFFFFFFFFFFFFFFFull, 0xFFFFFFF2FFFFFFFFull}/*13p*/
};

同時，為了保證被約減數 v 滿足 0≤v<p2 ，在模約減前還需要對輸入進行驗證。基於同樣的原因，我們還需要預計算 p2 的值：

/* pre-compute the value of p^2 check if the input satisfies input < p^2. */
static const BN_ULONG _sm2_p_256_sqr[] = {
    0x0000000000000001ULL, 0x00000001FFFFFFFEULL,
    0xFFFFFFFE00000001ULL, 0x0000000200000000ULL,
    0xFFFFFFFDFFFFFFFEULL, 0xFFFFFFFE00000003ULL,
    0xFFFFFFFFFFFFFFFFULL, 0xFFFFFFFE00000000ULL
};

在 64 位平台和部分支持 64 位無符號整型的 32 位平台上，由於 v[i] 滿足 0≤v[i]<232，因此可以使用 64 位無符號整形變量 accumulator 作為中間值存儲累加結果，從而在 v[0]-v[7] 參數上直接累加高位參數約化結果。以 v[0] 為例，其相應代碼如下：

        SM2_INT64 acc;         /* accumulator */

        acc = rp[0];
        acc += bp[8 - 8];
        acc += bp[9 - 8];
        acc += bp[10 - 8];
        acc += bp[11 - 8];
        acc += bp[12 - 8];
        acc += bp[13 - 8];
        acc += bp[14 - 8];
        acc += bp[15 - 8];
        acc += bp[13 - 8];
        acc += bp[14 - 8];
        acc += bp[15 - 8];    /*累加高位參數約化結果*/
        rp[0] = (unsigned int)acc; /*獲得結果的低32位*/
        acc >>= 32; /*進位部分右移32位，作為v[1]輸入的一部分*/

對於部分不支持 64 位無符號整型的 32 位平台，32 位整形變量由於數據溢出無法作為中間值保留進位結果，上述代碼將不能正確運行。此時需要藉助現有工具函數和銅鎖底層大數運算函數的支持，按照前文展示的算法逐一累加 s1~s14，每次還需要記錄進位 carry：

        /*
         * r_d += s2 + s6 + s7 + s8 + s9
         * s2 = (c15, c14, c13, c12, c11, 0, c9, c8)
         */
        sm2_set_256(t_d, buf.bn, 15, 14, 13, 12, 11, 0, 9, 8);
        carry += (int)bn_add_words(r_d, r_d, t_d, BN_SM2_256_TOP);
        /*
         * s6 = (c11, c11, c10, c15, c14, 0, c13, c12)
         */
        sm2_set_256(t_d, buf.bn, 11, 11, 10, 15, 14, 0, 13, 12);
        carry += (int)bn_add_words(r_d, r_d, t_d, BN_SM2_256_TOP);
        /*
         * s7 = (c10, c15, c14, c13, c12, 0, c11, c10)
         */
        sm2_set_256(t_d, buf.bn, 10, 15, 14, 13, 12, 0, 11, 10);
        carry += (int)bn_add_words(r_d, r_d, t_d, BN_SM2_256_TOP);
        /*
         * s8 = (c9, 0, 0, c9, c8, 0, c10, c9)
         */
        sm2_set_256(t_d, buf.bn, 9, 0, 0, 9, 8, 0, 10, 9);
        carry += (int)bn_add_words(r_d, r_d, t_d, BN_SM2_256_TOP);
        /*
         * s9 = (c8, 0, 0, 0, c15, 0, c12, c11)
         */
        sm2_set_256(t_d, buf.bn, 8, 0, 0, 0, 15, 0, 12, 11);
        carry += (int)bn_add_words(r_d, r_d, t_d, BN_SM2_256_TOP);

最後處理進位，得到最終結果，此處變量 mask 的作用是減少代碼中不必要的分支，儘可能提高其抗側信道攻擊強度：

    mask =
        0 - (PTR_SIZE_INT) (*u.f) (c_d, r_d, _sm2_p_256[0], BN_SM2_256_TOP);
    mask &= 0 - (PTR_SIZE_INT) carry;
    res = c_d;
    res = (BN_ULONG *)(((PTR_SIZE_INT) res & ~mask) |
                       ((PTR_SIZE_INT) r_d & mask));
    sm2_cp_bn(r_d, res, BN_SM2_256_TOP);
    r->top = BN_SM2_256_TOP;
    bn_correct_top(r);

測試

正確性測試

為了驗證快速模約減算法的正確性，我們在測試環節設計了相應的單元測試。該測試的核心思路是，隨機生成一批有限域大整數 ai，bi，分別使用銅鎖提供的默認方法和本文實現的快速模約減方法計算 ai*bi mod p，然後比較二者計算結果是否相等：

    /*
     * Randomly generate two numbers in the prime field and multiply them，then compare the results of fast modular reduction and conventional algorithms.
     */
    for (i = 0; i < 100; i++){
        if (!TEST_true(BN_priv_rand_range_ex(a, p, 0, ctx))
            || !TEST_true(BN_priv_rand_range_ex(b, p, 0, ctx))
            || !TEST_true(BN_mul(ab_fast, a, b, ctx))
            || !TEST_true(BN_sm2_mod_256(ab_fast, ab_fast, p, ctx))
            || !TEST_true(BN_mod_mul(ab, a, b, p, ctx))) {
            goto done;
        }

        if (!TEST_int_eq(BN_ucmp(ab, ab_fast), 0)){
            goto done;
        }
    }

可以使用如下命令調用測試：

make test TESTS="test_mod_sm2"

測試結果：

➜  Tongsuo git:(sm2p256) ✗ make test TESTS="test_mod_sm2"
/Library/Developer/CommandLineTools/usr/bin/make depend && /Library/Developer/CommandLineTools/usr/bin/make _tests
10-test_mod_sm2.t .. ok   
All tests successful.
Files=1, Tests=1,  1 wallclock secs ( 0.00 usr  0.01 sys +  0.07 cusr  0.02 csys =  0.10 CPU)
Result: PASS

性能測試

為了充分比較快速模約減算法的性能，我們選擇比較 SM2 有限域運算中較常用的模乘法運算作為測試單元，測試使用了 SM2 快速模約減函數 BN_sm2_mod_256、簡單模約減函數 BN_nnmod 的模乘函數 ossl_ec_GFp_field_mul 和通用蒙哥馬利模乘函數 BN_mod_mul_montgomery 的模乘法運算耗時。測試在 Apple M2 pro 平台上進行，測試數據如下表所示：

測試結果表明，使用 SM2 快速模約減函數的模乘法耗時最少，相較於簡單模約減能夠減少 81.34% 的時間開銷，即使對使用了彙編優化的蒙哥馬利模乘運算，在計算時間上仍有 29.91% 的優勢。

下篇 SM2 算法性能優化實踐系列文章我們將介紹“快速模逆元算法實現”，敬請期待！

文中鏈接

[1]白國強等人提出的快速模約減算法：https://ieeexplore.ieee.org/document/7011249