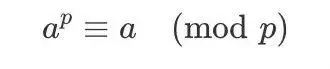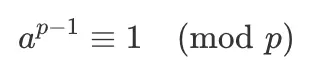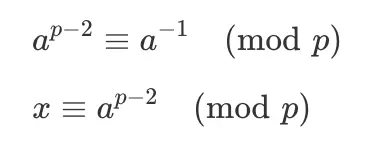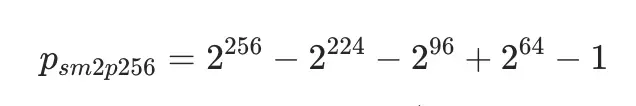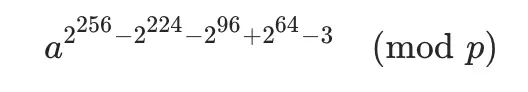模逆元的概念

在數學上，乘法逆元有一個更加廣為人知的別名“倒數”。也就是説，對於實數 a，其倒數 a-1 滿足 a*a-1=1。由於 1 是實數域的乘法單位元，故而倒數 a-1 為實數 a 的乘法逆元。

而在有限域模運算中，乘法逆元的定義要更復雜一些：如果 a 和 m 都是正整數且滿足 gcd(a,m)=1，那麼在模 m 意義下，存在一個整數 b，使得 ab≡1(mod m)，此時 b 就是 a 在模 m 運算下的逆元，常表示為 a-1，簡稱為模逆元。 由於引入了模運算，在實數域上簡單求倒數獲得逆元的方法並不能直接求得有限域上的模逆元，需要改用更為複雜的方式求解運算結果。

在 SM2 數字簽名算法中，存在兩個必須計算模逆元的步驟：一是將橢圓曲線公鑰點 PK 由仿射座標轉化為雅可比座標時，需要計算 z 軸座標 z1 對素數域參數 p 的模逆元；二是在簽名計算過程中，需要求解私鑰 dA+1 對橢圓曲線階數 n 的模逆元。由於模逆元的計算非常複雜，是橢圓曲線中開銷最大的單體運算 （無任何優化時計算耗時是模乘法的數千倍） ，且運算處於數字簽名算法流程的關鍵鏈路上， 因此是制約 SM2 數字簽名性能的瓶頸之一。目前，銅鎖項目為 SM2 數字簽名算法提供了通用的模逆元優化實現，尚未針對 SM2 曲線實現特定優化，存在可以進一步優化提升的空間。

優化方案比較選型

在數學上，有兩種算法可以快速地計算模逆元，它們分別是拓展歐幾里得算法和基於費馬小定理的求解算法。下面我們簡要介紹這兩類算法，討論各算法的優缺點以及在銅鎖的工程實現中選擇基於費馬小定理的求解算法的原因。

1 拓展歐幾里得算法求解模逆元

用於求解最大公約數的歐幾里得算法最早在歐幾里得的《幾何原本》中被提出，拓展歐幾里得算法是對這一古老算法的擴展。在求解最大公約數的基礎上，拓展歐幾里得算法通過收集輾轉相除過程中的餘式，求得線性方程 ax+by=gcd(a,b) 的整數解。由於階數 n 是一個質數，因此 gcd(a,n)=1，那麼該線性方程即轉化為 ax+ny=1，恰巧是同餘線性方程 ax≡1(mod n) 的一般表示形式，所求的 x 即為 a 的模 n 逆元。

對於現代計算機而言，拓展歐幾里得算法的一個缺點是在計算過程中存在大量除法運算，而 CPU 在處理除法運算時的效率通常比其他基本運算 （如加、減、乘） 要低得多。針對這一缺陷，約瑟夫 · 斯提芬於 1967 年提出了二進制拓展歐幾里得算法[1], 該算法用簡單的移位操作和減法代替了複雜的除法運算。下面是利用二進制拓展歐幾里得算法求模 n 逆元的偽代碼：

拓展歐幾里得算法求解模逆元的優點是：可以求解任意模數下的逆元，不受模數是否為素數的限制；算法效率高，相較於費馬小定理求模逆元有一定的性能優勢。但是，拓展歐幾里得算法相應的也存在一些缺點：實現代碼較為複雜，容易出錯；代碼中有大量的分支和判斷語句，難以實現恆定時間 （Constant time） 算法，對於側信道攻擊的抵抗較弱，在密碼學算法中可能會導致關於私鑰或明文的信息發生泄漏。

2 費馬小定理求解模逆元

費馬小定理 （Fermat's little theorem） 是數論中的一個重要定理，最早由數學家費馬於 1636 年提出。定理的內容是：假如 a 是一個整數，p 是一個質數，那麼有：

在 SM2 曲線中，數 a 和參數 n，p 滿足 a<p，n<p<2n，且 p 和 n 均為素數，因此數 a，n，p 三者兩兩互質。此時，費馬小定理有如下形式：

數 a，p 互質，那麼有 ax=1(mod n)，聯立可得：

也就是説，若要計算數 a 對素數 p 的模逆元 x，只需要求解 ap-2mod p 即可。藉助費馬小定理的轉換，模逆元求解的過程即轉化為使用模乘與模平方運算構造 ap-2 的過程，大大簡化了計算。

運用費馬小定理求解模逆元的優點是：算法簡單，運算過程只需要模乘與模平方運算參與，沒有進位和分支操作，很容易實現恆定時間算法，在抵抗側信道攻擊方面相較於拓展歐幾里得算法有較大優勢；相應地，運用費馬小定理求解模逆元的缺點有：適用範圍較窄，只適用於模數為素數的情況；模數較大時，需要計算的冪次比較大，相較於使用拓展歐幾里得算法求解模逆元的性能稍劣。

3 方案選型

在銅鎖中，SM2 數字簽名算法的快速模逆元優化實現最終選擇了基於費馬小定理求解模逆元的算法，主要原因有以下兩點：

作為銅鎖國密通信協議、國密證書籤發等關鍵應用的基礎，SM2 數字簽名算法在實現時應尤其注意安全性，特別是在抗側信道攻擊方面，應精心設計以避免私鑰泄露；基於費馬小定理求解模逆元的算法在設計恆定時間算法、抵抗側信道攻擊方面有較大優勢。

費馬小定理求模逆元的一些缺點在 SM2 算法的優化實現中能夠有效規避。例如，SM2 曲線的參數 n，p 均為素數，滿足費馬小定理只適用於模數為素數的條件；對於性能問題，在具體實現時，可以通過加法鏈構造 ap-2 減少計算模逆元所需的模乘與模平方運算次數，彌補費馬小定理求逆的些許性能劣勢。

算法實現

本文以 SM2 素數域模逆元求解為例，介紹費馬小定理求解模逆元的具體實現。這裏首先給出 SM2 素數域參數 p：

由費馬小定理可得，若要計算正整數 a 對模數 p 的逆元 a-1，只需計算：

該數的冪次非常大，如果採用常規方式構造，效率極低，這裏我們採用加法鏈的思想以實現快速求冪。加法鏈求冪是一種快速求冪的方法，它的基本思想是將指數按二進制分解，並將冪運算分解為多個小冪數相乘的形式，從而減少冪運算的次數。前文提到，費馬小定理求解模逆元的運算過程可以分解為模乘法和模平方運算，這裏我們記模乘法次數為 xM，模平方次數為 yS，那麼加法鏈求冪的時間複雜度可以用 xM+yS 來衡量。

儘管使加法鏈求冪時間複雜度最優的問題是一個 NP-hard 問題，且證明某求解鏈路是否為最優解也非常困難，但密碼學界針對常見的橢圓曲線參數已經提出了許多較優的加法鏈。我們通過比較同一曲線的不同加法鏈路和相近曲線的較優鏈路，再進一步比較不同方案所需的中間值數量，可以比選出一個當前最優解。目前，在針對 SM2 曲線參數 p 的模逆元加法鏈研究中，一個較優解是朱輝等人提出的算法[2]，此算法的時間複雜度為 255M+14S，需要 4 個變量作為中間值，具體如下：

在計算 ap-2 時，另一個需要仔細考慮的是中間值溢出問題。在本系列（二）中提到，快速模約減的輸入必須小於 p2，由於 0<a<p，因此在每一次乘法或平方運算後，都需要立刻調用快速模約減函數將中間值約化到 [0,p) 範圍內，以避免中間值溢出導致結果出錯的情況。最終銅鎖實現的快速模逆元算法如下所示：

static void felem_inv(felem out, const felem in)
{
    felem t0, t1, t2, t3;
    felem ftmp;
    longfelem tmp;
    unsigned i;

    /* Step 1: t0 = a^3 = (2^2 - 2^0) * a */
    felem_square(tmp, in);
    felem_reduce(ftmp, tmp);
    felem_mul(tmp, ftmp, in);
    felem_reduce(t0, tmp);
    /* Step 2: t1 = t0^2 * a = (2^3 - 2^0) * a */
    felem_square(tmp, t0);
    felem_reduce(ftmp, tmp);
    felem_mul(tmp, ftmp, in);
    felem_reduce(t1, tmp);

    /* 部分中間代碼略，完整代碼可見/crypto/ec/sm2p256.c*/
    
    /* Step 14: t2= ((t3^(2^32) * t0)^(2^64) * t0)^(2^94) = (2^254 - 2^222 - 2^94) * a */
    felem_assign(ftmp, t3);
    for (i = 0; i < 32; i++) {
        felem_square(tmp, ftmp);
        felem_reduce(ftmp, tmp);
    }          
    felem_mul(tmp, ftmp, t0);
    felem_reduce(ftmp, tmp);
    for (i = 0; i < 64; i++) {
        felem_square(tmp, ftmp);
        felem_reduce(ftmp, tmp);
    }
    felem_mul(tmp, ftmp, t0);
    felem_reduce(ftmp, tmp);
    for (i = 0; i < 94; i++) {
        felem_square(tmp, ftmp);
        felem_reduce(ftmp, tmp);
    }
    felem_assign(t2, ftmp);
    /* Step 15: out = (t1 * t2)^4 * a = (2^256 - 2^224 - 2^96 + 2^64 -1) * a */
    felem_mul(tmp, t1, t2);
    felem_reduce(ftmp, tmp);
    felem_square(tmp, ftmp);
    felem_reduce(ftmp, tmp);
    felem_square(tmp, ftmp);
    felem_reduce(ftmp, tmp);
    felem_mul(tmp, ftmp, in);
    felem_reduce(out, tmp);
}

可以看到，最終實現的代碼沒有進位和分支，且代碼實現時僅調用了素數域運算的乘法、平方、快速約減等函數，由於這些函數都是恆定時間的，因此最終銅鎖所實現的快速模逆元函數也是恆定時間的，從算法實現層面阻止了惡意攻擊者通過計時攻擊獲取用户私鑰的可能性。

總結與展望

關於銅鎖 SM2 算法性能優化實踐的內容大致就是這些。在實現優化後，銅鎖 SM2 數字簽名算法的性能取得了不小的進步，在國密開源產品中處於領先地位，同時極大拉近了與國際主流非對稱算法 （例如 ed25519、nistp256） 成熟工程實現的性能差距，有利於國家商用密碼在國內的進一步落地推廣，實現行業信息系統安全的自主可控。

未來，銅鎖還將持續追蹤密碼學學術界的最新動向，積極推動學術研究成果在銅鎖項目中落地，為用户提供性能更優、安全性更好的安全產品。歡迎開源社區的愛好者們與我們一起，攜手共建銅鎖社區良好的項目生態！

歡迎加入銅鎖社區交流釘釘羣：44810299

更多文檔可關注銅鎖官方語雀：https://www.yuque.com/tsdoc

【 文中鏈接 】

[1]二進制拓展歐幾里得算法：https://www.sciencedirect.com/science/article/abs/pii/0021999...

[2]針對素數 PSCA-256 的快速模逆算法：https://jeit.ac.cn/cn/article/doi/10.11999/JEIT211049