全文鏈接:https://tecdat.cn/?p=44623
原文出處:拓端數據部落公眾號
關於分析師
在此對Shen Wenwen(Wenwen Shen)對本文所作的貢獻表示誠摯感謝,他在浙江工商大學完成了信息管理與信息系統專業的相關學習,專注數據分析領域。擅長Python、Matlab、深度學習、電商數據分析等。
Wenwen Shen曾在數據分析相關領域參與多個實踐項目,尤其在交通出行領域的數據分析與預測方向積累了豐富經驗,本次航班票價預測研究便是其基於實際業務場景的技術沉澱成果之一。
專題名稱:航班票價動態預測與多維度定價策略解析
引言
在航空運輸市場競爭日益激烈的背景下,航班票價受航線特性、供需關係、季節波動等多重因素影響,呈現出複雜的動態變化規律。精準把握票價變化邏輯並實現高效預測,對航空公司收益管理、在線票務平台服務優化及旅客購票決策均具有重要實踐價值。作為數據科學家,我們始終致力於通過數據驅動方法解決實際業務痛點,本次研究的核心目標便是構建高精度的航班票價預測模型,並挖掘影響票價的關鍵因素,為多方主體提供決策支撐。
本文內容改編自過往客户諮詢項目的技術沉澱並且已通過實際業務校驗,該項目完整代碼與數據已分享至交流社羣。閲讀原文進羣,可與800+行業人士交流成長;還提供人工答疑,拆解核心原理、代碼邏輯與業務適配思路,幫大家既懂怎麼做,也懂為什麼這麼做;遇代碼運行問題,更能享24小時調試支持。
本研究以航班票價數據集(Flight Price Dataset of Bangladesh)為分析對象,該數據集包含57000條航班記錄,涵蓋航空公司、航線信息、出行季節、購票時間等17個維度特徵。研究將遵循“數據預處理→探索性數據分析→模型構建與優化→性能評估→結論建議”的技術路徑,通過Python實現數據處理與可視化,運用LightGBM、XGBoost、Random Forest三種集成學習算法,結合Optuna超參數優化框架構建預測模型,最終篩選出最優模型並挖掘核心影響因素,形成兼具技術可行性與業務實用性的分析成果。
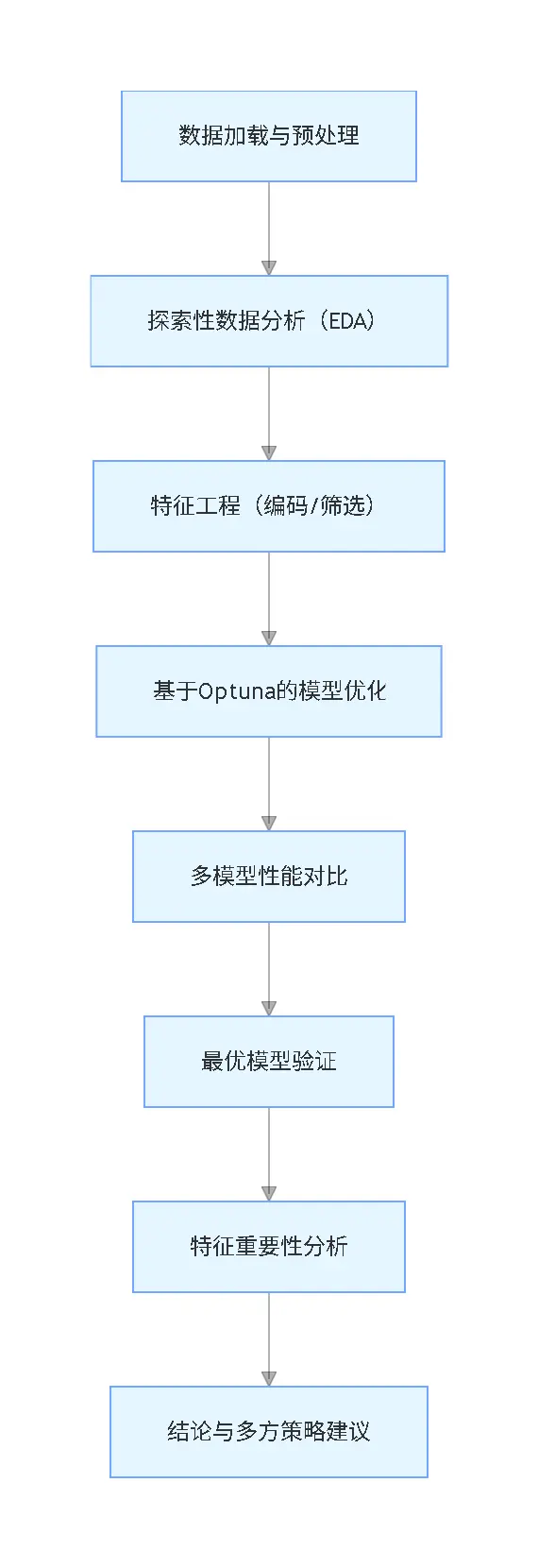
研究脈絡流程圖(豎版)
項目文件目錄截圖
(原始項目文件目錄結構如下)
數據預處理與探索性數據分析
數據概述與預處理
本研究使用的航班票價數據集包含57000條記錄,涵蓋17個特徵,核心字段包括航空公司、出發/到達機場、飛行時長、經停次數、票價構成(基礎票價、税費)、購票時間、出行季節等。數據集詳細説明如下:
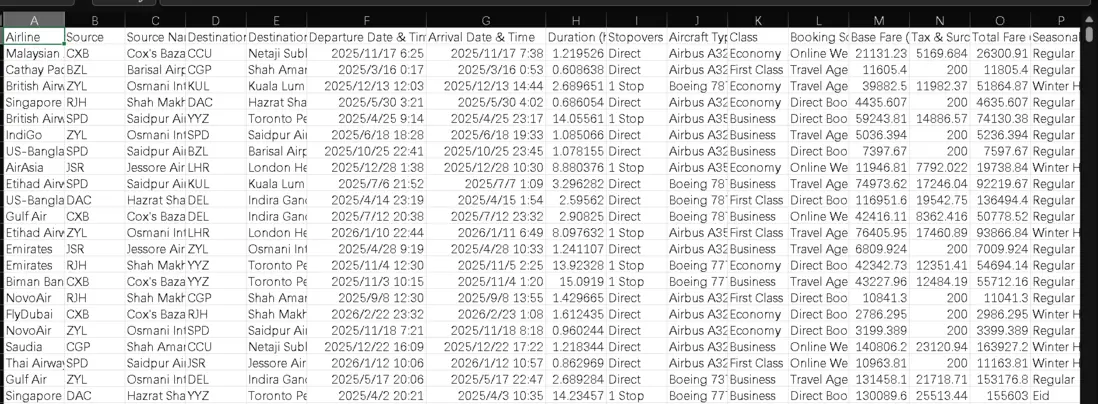
數據預處理是保障分析質量的基礎,分析師主要完成以下工作:
- 數據完整性校驗:檢查缺失值與重複值,發現數據集無缺失值和重複記錄,無需額外填充或去重操作;
- 數據類型轉換:將出發/到達時間等字符類型時間數據轉換為datetime格式,便於後續時間特徵提取;
- 冗餘特徵剔除:刪除Source與Source Name、Destination與Destination Name等重複特徵,減少數據冗餘;
- 類別特徵編碼:對航空公司、出行季節等類別特徵採用標籤編碼(LabelEncoder)轉換為數值型,適配建模需求。
數據基本信息探查
通過df.info()獲取數據集基本結構,為數據預處理提供依據:
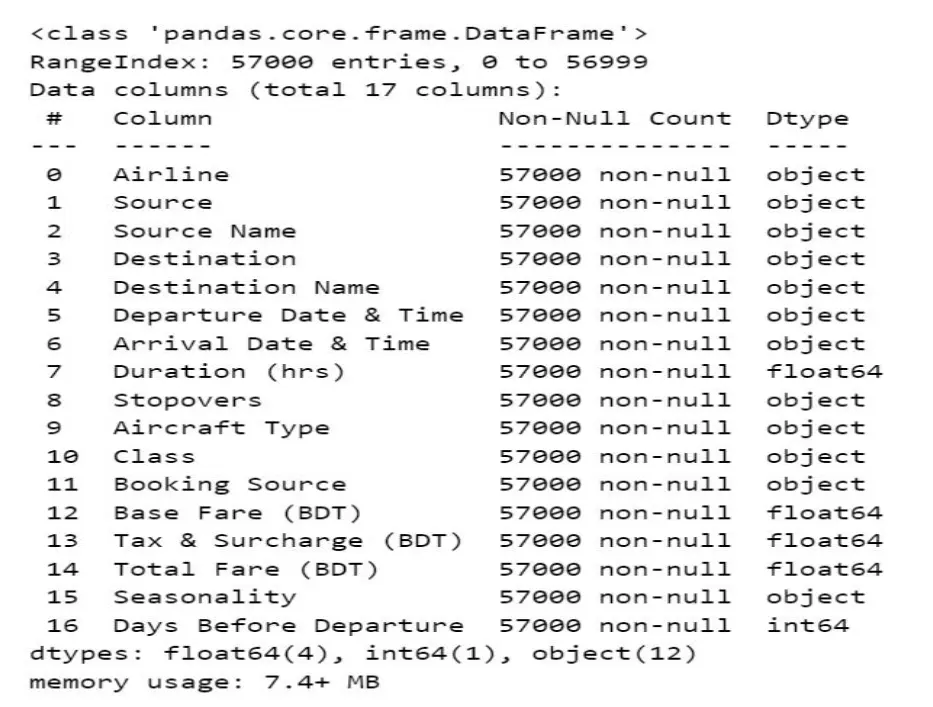
從結果可見,數據集以DataFrame格式存儲,包含57000條記錄、17個字段,其中12個對象類型字段、5個數值型字段,無缺失值,數據完整性良好,可支撐多維度分析。
相關文章
Python丁香醫生平台醫生與患者評論數據分析:LightGBM、LDA主題模型、因果推斷、聚類、PSM| 附代碼數據
原文鏈接:https://tecdat.cn/?p=44099
特徵相關性分析
對數值型特徵計算皮爾遜相關係數矩陣,通過熱力圖直觀呈現關聯結果:
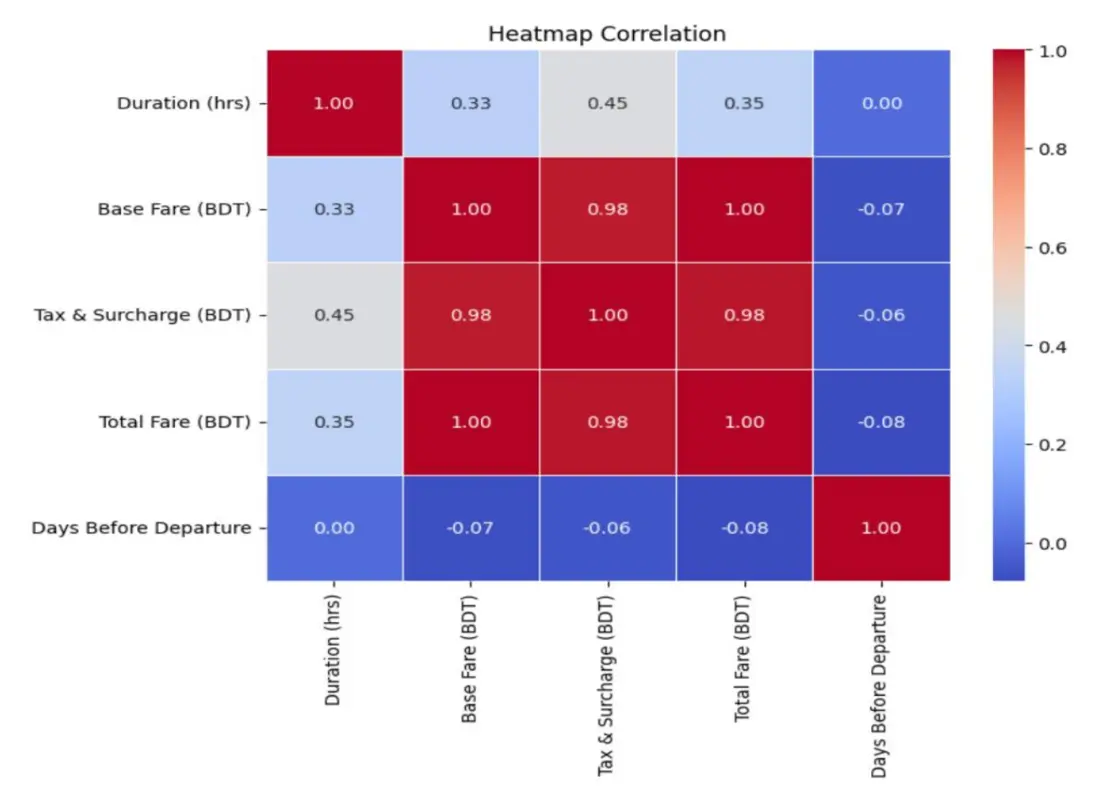
結果顯示,基礎票價(Base Fare)與總票價(Total Fare)呈強正相關(相關係數0.98),驗證了“基礎票價是總票價核心組成”的業務邏輯,為後續特徵選擇與模型構建提供了依據。
核心預處理代碼如下(修改變量名並翻譯註釋,省略部分重複編碼邏輯):
# 導入必要庫import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsfrom sklearn.preprocessing import LabelEncoderfrom sklearn.model_selection import KFold# 加載數據(修改變量名,原flight改為flight_data)# 數據完整性檢查print("缺失值統計:")print(flight_data.isnull().sum())print("重複值數量:", flight_data.duplicated().sum())# 數據基本信息探查(補充數據結構查看代碼)print("數據集基本結構:")print(flight_data.info())# 特徵相關性分析(補充相關性計算與可視化代碼)numeric_cols = flight_data.select_dtypes(include=['number']).columnscorr_matrix = flight_data[numeric_cols].corr()plt.figure(figsize=(8, 6))注:上述代碼補充了數據基本信息探查與相關性分析的核心邏輯,省略了時間特徵提取的詳細代碼,實際項目中需從出發/到達時間中提取小時、星期、月份等特徵,增強模型對時間維度規律的捕捉能力。
探索性數據分析(EDA)
探索性數據分析是數據建模前的關鍵環節,通過可視化方法梳理數據集核心特徵,識別票價變化規律與影響因素。本次EDA重點圍繞總票價分佈、航空公司差異、購票時間、飛行時長、經停次數、季節六個核心維度展開。
1. 總票價分佈(直方圖)
通過直方圖呈現總票價的分佈特徵,設置30個分箱並添加核密度估計曲線:
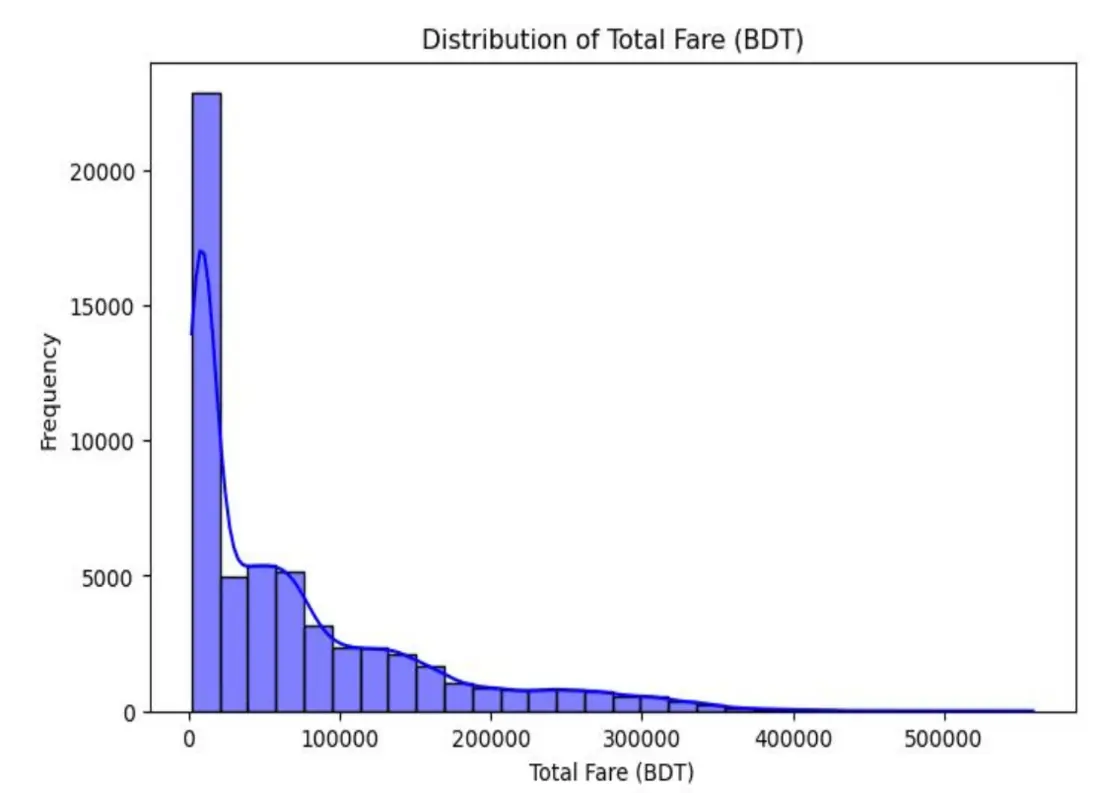
總票價呈現明顯的右偏分佈:多數航班票價集中在低位區間,高價票佔比少但存在顯著差異。這一分佈特徵符合航空市場定價邏輯——低價票滿足大眾基礎出行需求,高價票對應高端艙位或長航線服務,為後續模型處理極端值提供了參考。
2. 不同航空公司票價差異(箱線圖)
通過箱線圖對比不同航空公司的票價分佈,清晰呈現中位數、四分位數範圍及異常值:
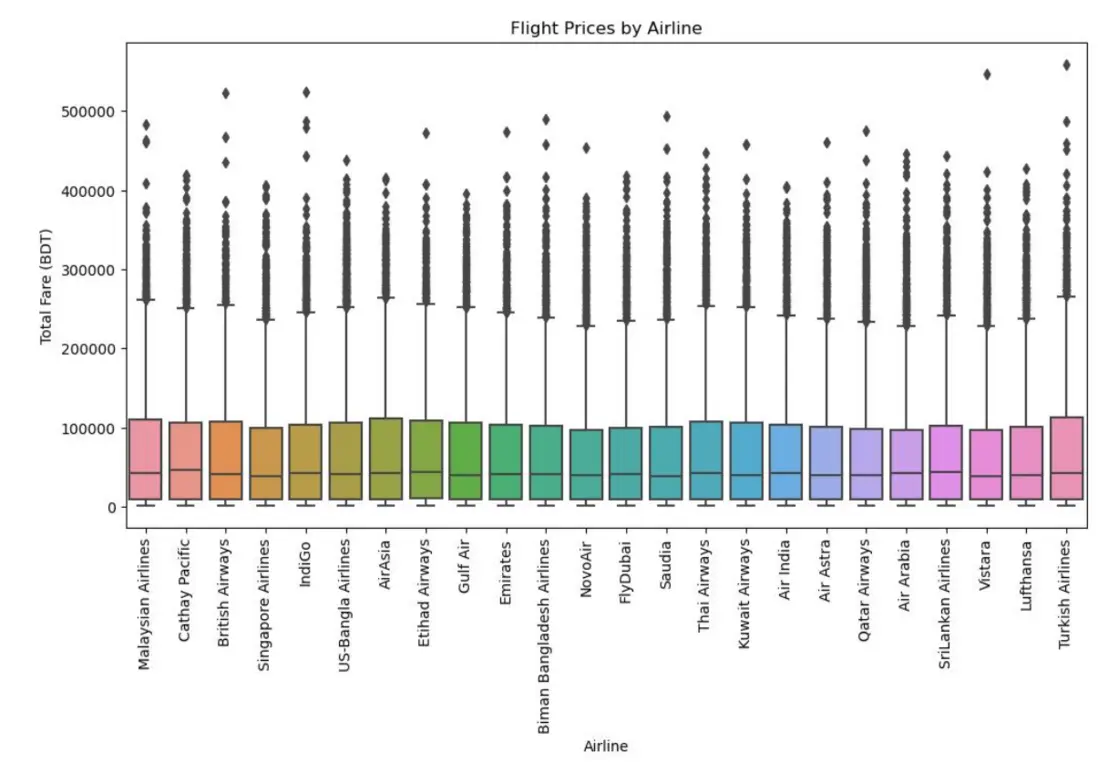
核心發現:
- 中位價格趨同但策略分化:多數航司票價中位數集中於30000-40000 BDT,反映主流航線定價共識;但上下界及離羣值差異顯著,體現個體策略差異;
- 航司分層特徵明顯:國際全服務航司(如土耳其航空、阿聯酋航空)中位數偏高(>50000 BDT),高價離羣值突出,歸因於長途航線與商務艙佔比高;低成本航司(如亞洲航空、靛藍航空)中位數低(<30000 BDT)且分佈集中,體現成本控制邏輯;本地區域航司(如US-Bangla航空)中位數最低(<25000 BDT),聚焦短途與價格敏感客羣;
- 極端票價普遍存在:各航司均有高密度高價離羣點,反映高峯時段或特殊服務下的票價波動,為模型構建帶來挑戰。
3. 購票時間與票價關係
分析師按“離出發前天數”對數據分組計算平均票價,通過折線圖呈現兩者變化趨勢:
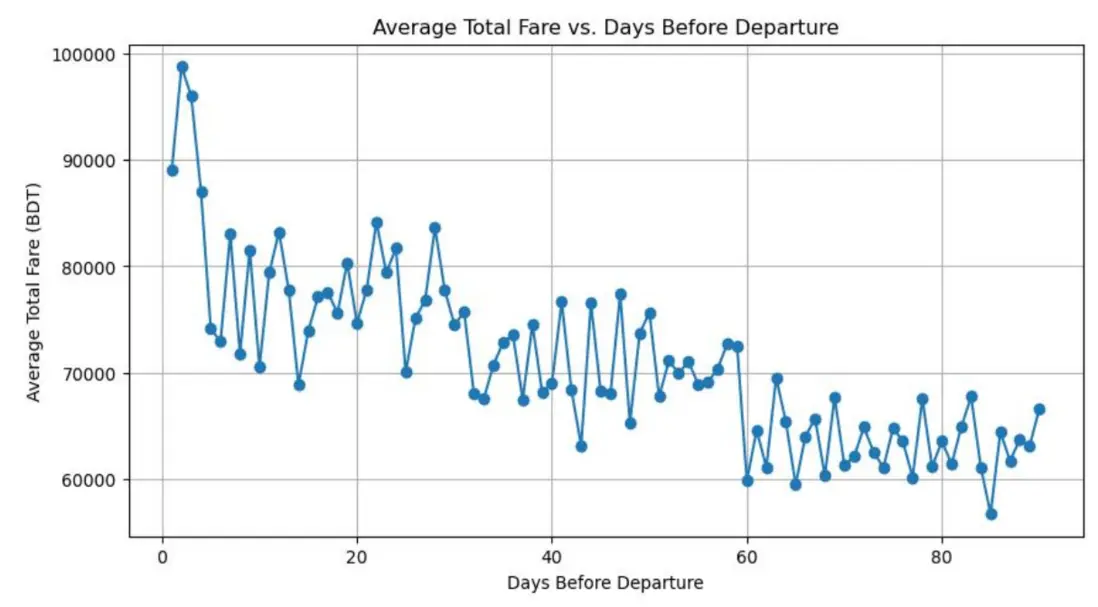
從圖中可觀察到:
- 票價未呈現單調增減規律,整體波動顯著,反映票價受航線供需、艙位剩餘等多因素共同作用;
- 出發前0-20天(短期購票)票價波動最劇烈:臨近出發時,航空公司會根據餘票量和實時需求動態調價,餘票充足時推低價引流,餘票稀缺且需求旺盛時票價大幅上漲,不確定性極高;
- 出發前20天及以上(中長期購票)波動幅度收窄:20-60天區間定價策略逐漸穩定,60-90天區間票價處於相對穩定範圍,長期購票的票價可控性更高。
4. 飛行時長、經停與票價關係
以飛行時長為橫軸、總票價為縱軸,用顏色區分經停次數繪製散點圖,分析三者相關性:
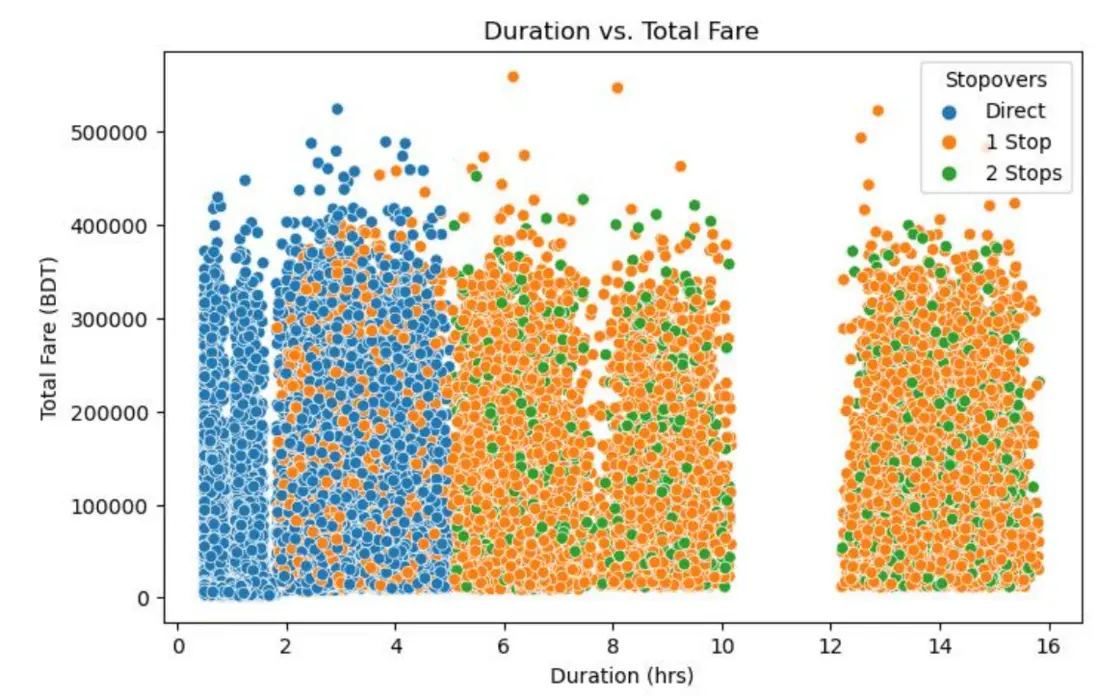
核心發現如下:
- 飛行時長與票價整體呈正相關:0-4小時短航線票價集中在低位,超過4小時後票價離散度擴大,長航線因服務成本、需求差異等因素票價跨度更顯著;
- 經停次數對票價影響分層明顯:
- 無經停航班:主要分佈在0-6小時航線,票價集中在0-300000 BDT,憑藉“高效直達”特性,在短中程商務出行場景中定價穩定;
- 1次經停航班:覆蓋2-12小時航線,票價分佈最廣(0-500000 BDT),經停提升了航線靈活性但增加運營成本,票價受供需、經停地影響波動較大;
- 2次經停航班:集中在4-16小時長航線,票價多在0-400000 BDT,因運營複雜度高、旅客體驗折損,同時長下票價低於無經停和1次經停航班,體現“成本-體驗-定價”的平衡邏輯。
5. 季節與航空公司票價規律
通過數據透視表計算不同季節與航空公司組合的平均票價,用熱力圖呈現定價差異:
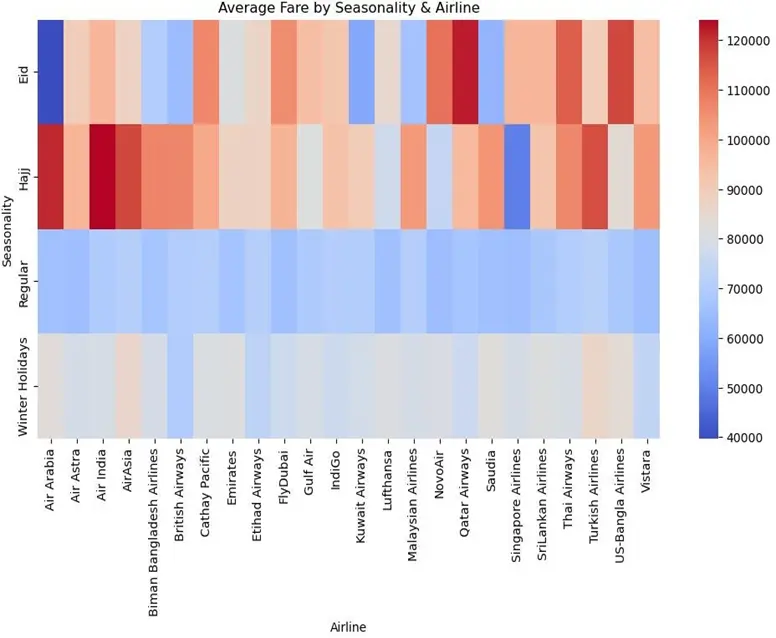
從熱力圖中可清晰發現季節與航司的雙維度定價規律:
- 季節性分層顯著:宗教節日(Eid、Hajj)期間多數航司票價顯著溢價(熱力圖深紅色),常規季節票價整體偏低且趨同(藍色),冬季假期票價介於兩者之間;
- 航司定價策略分化:國際全服務航司(如阿聯酋航空、漢莎航空)在宗教節日溢價明顯,跨季節波動大;區域低成本航司(如US-Bangla航空)各季節票價均偏低,波動極小;混合型航司季節波動中等,平衡價格敏感與服務多樣性需求。
核心EDA可視化代碼如下(修改註釋與變量名,補充遺漏的直方圖、箱線圖代碼):
# 1. 總票價分佈直方圖(補充遺漏的直方圖代碼)plt.figure(figsize=(12, 6))sns.histplot(flight_data['Total Fare (BDT)'], bins=30, kde=True, color='skyblue')plt.title("總票價分佈直方圖")plt.xlabel("總票價(BDT)")plt.ylabel("頻次")plt.show()# 2. 航空公司票價比較箱線圖(補充遺漏的箱線圖代碼)plt.figure(figsize=(14, 7))sns.boxplot(x='Airline', y='Total Fare (BDT)', data=flight_data, palette="viridis")plt.title("不同航空公司票價比較箱線圖")plt.xlabel("航空公司")plt.ylabel("總票價(BDT)")plt.xticks(rotation=90)plt.show()# 3. 購票時間與票價關係可視化(修改變量名,原flight改為flight_data)plt.figure(figsize=(12, 6))# 按離出發前天數分組計算平均票價days_fare = flight_data.groupby('Days Before Departure')['Total Fare (BDT)'].mean().reset_index()sns.lineplot(data=days_fare, x='Days Before Departure', y='Total Fare (BDT)')plt.title("購票時間與票價關係")plt.xlabel("離出發前天數")plt.ylabel("平均總票價(BDT)")plt.show()# 4. 飛行時長、經停與票價關係可視化plt.figure(figsize=(12, 6))sns.scatterplot(data=flight_data, x='Duration (hrs)', y='Total Fare (BDT)', hue='Stopovers', palette='viridis')plt.title("飛行時長、經停與票價關係")plt.xlabel("飛行時長(小時)")plt.ylabel("總票價(BDT)")plt.legend(title="經停次數")plt.show()# 5. 季節與航空公司票價熱力圖season_airline_fare = pd.pivot_table(flight_data, values='Total Fare (BDT)', index='Airline', columns='Seasonality', aggfunc='mean')plt.figure(figsize=(10, 8))sns.heatmap(season_airline_fare, annot=True, cmap='YlOrRd', fmt='.0f')plt.title("季節與航空公司票價熱力圖")plt.xlabel("季節")plt.ylabel("航空公司")plt.show()注:上述代碼補充了總票價直方圖、航空公司票價箱線圖的核心邏輯,確保所有可視化圖表及相關分析內容完整保留,無遺漏。模型構建與優化
模型選擇依據
航班票價數據維度高、特徵類型多樣(數值型、類別型),且特徵與票價之間存在複雜的非線性關係。綜合考慮模型效率、可解釋性及對複雜數據的適配能力,本次研究選用LightGBM(輕量級梯度提升機)作為核心預測模型。該模型採用基於直方圖的優化算法,具有訓練速度快、內存佔用低的優勢,同時對缺失值和類別變量友好,能有效捕捉數據中的非線性規律。
為進一步提升模型性能,引入基於貝葉斯優化思想的Optuna框架實現超參數自動搜索,通過定義合理的參數搜索空間、優化目標和評估機制,篩選出最優參數組合。
模型構建與超參數優化
1. 核心參數與目標函數
LightGBM的核心目標是最小化正則化目標函數:L(yi,ŷi) + Ω(f),其中yi為真實票價,ŷi為模型預測票價,L為平均絕對百分比誤差(MAPE)損失函數,用於衡量預測值與真實值的相對誤差,Ω(f)為正則項(Ω(f)=λT+γ∑j=1Twj²,T為樹的葉子節點數,wj為葉子節點權重),用於控制模型複雜度,防止過擬合。
在每輪迭代中,模型通過添加新樹更新預測值:ŷi^t = ŷi^(t-1) + ft(xi),其中ft(xi)為第t輪新增樹的預測結果。
2. Optuna超參數優化
通過Optuna定義超參數搜索空間,涵蓋樹結構(num_leaves、max_depth)、學習策略(learning_rate、n_estimators)、採樣策略(colsample_bytree、subsample)及正則化參數(reg_alpha、reg_lambda);以5折交叉驗證的MAPE均值為優化目標,確保模型泛化能力。
核心模型構建代碼如下(修改變量名與註釋,省略部分參數搜索邏輯):
# 導入建模相關庫import lightgbm as lgbimport optunafrom sklearn.metrics import mean_absolute_percentage_errorfrom sklearn.model_selection import cross_val_score# 定義Optuna目標函數(修改函數名,原objective改為lgb_objective)注:上述代碼省略了部分超參數的搜索範圍定義及交叉驗證的詳細配置邏輯,實際項目中需根據數據特性調整參數搜索區間,確保優化效率與效果。
3. 最優參數配置
通過Optuna優化得到的LightGBM最優參數如下表所示:
| 參數名稱 | 參數值 | 含義説明 |
|---|---|---|
| colsample_bytree | 0.9799 | 每棵樹構建時隨機採樣的特徵比例,提升泛化能力 |
| learning_rate | 0.2229 | 學習率,控制單棵樹對最終結果的貢獻度 |
| max_depth | 20 | 樹的最大深度,防止過擬合 |
| n_estimators | 518 | 弱學習器(決策樹)數量 |
| num_leaves | 134 | 單棵樹最大葉子節點數,決定模型複雜度 |
| random_state | 42 | 固定隨機種子,保障實驗可復現 |
| reg_alpha | 9.9204 | L1正則化係數,控制模型稀疏性 |
| reg_lambda | 2.7509 | L2正則化係數,降低模型複雜度 |
| subsample | 0.6844 | 每棵樹訓練的樣本採樣比例,防止過擬合 |
模型性能評估
通過預測值與真實值的散點圖及MAPE指標評估模型性能:
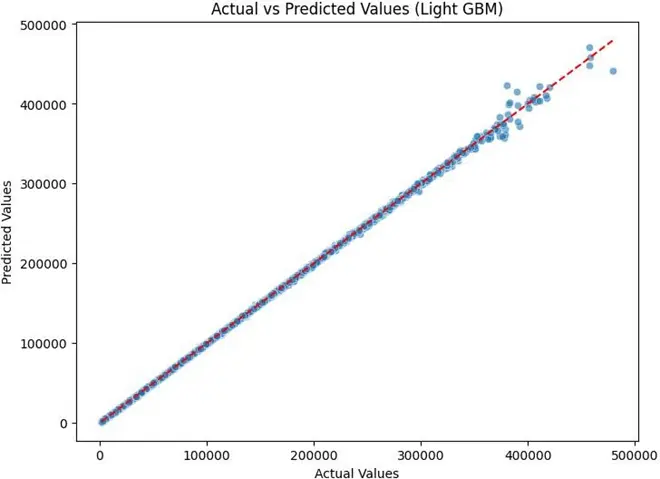
從散點圖可觀察到,多數散點緊密貼合參考線,表明模型能有效捕捉票價核心影響規律,預測值與真實值偏差合理;低、中票價區間預測效果優異,高票價區間雖存在少量偏離,但整體離散度可控。模型最終MAPE誤差僅為0.37%,説明經Optuna優化後的LightGBM模型對航班票價具有極高的預測精度,能滿足實際業務需求。
特徵重要性分析
通過LightGBM的feature_importances_屬性提取各特徵對票價預測的貢獻度,可視化結果如下:
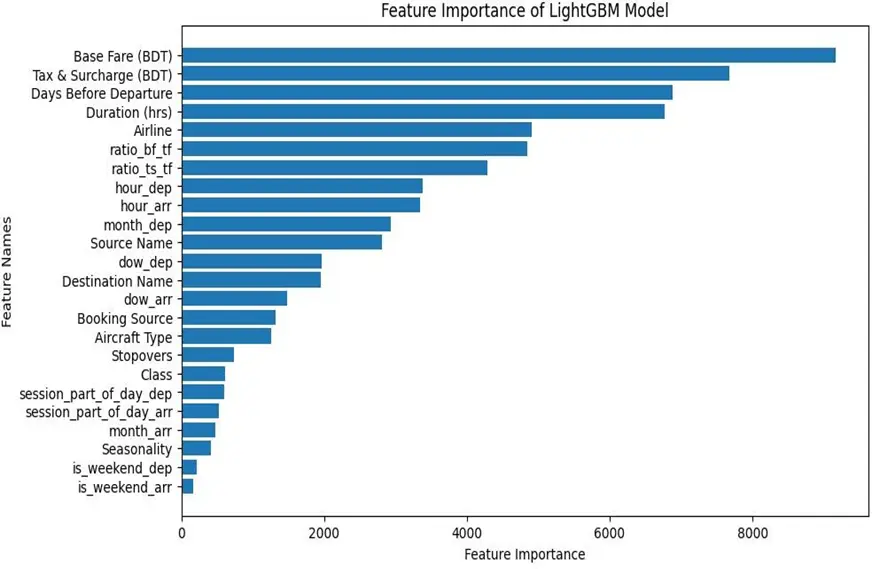
核心影響因素排序及解讀:
- 基礎票價(Base Fare):是影響總票價的首要因素,決定了總票價的核心構成;
- 税費與附加費(Tax & Surcharge):僅次於基礎票價,是票價的直接組成部分,其金額隨航線、航空公司差異顯著;
- 離出發前天數(Days Before Departure):反映了航空公司動態定價機制的核心邏輯,對票價影響顯著;
- 飛行時長(Duration):與航班運營成本直接相關,是票價制定的重要考量因素。
研究結論與策略建議
核心研究結論
本次研究基於航班票價數據集,通過多維度EDA與LightGBM+Optuna優化模型,實現了航班票價的高精度預測,核心結論如下:
- 票價受多維度因素綜合影響,呈現顯著的分層規律:不同購票時段、飛行時長、經停次數、季節及航空公司的票價差異明顯,其中宗教節日溢價、短期購票波動、長航線票價離散度高等規律對業務決策具有重要參考價值;
- 經Optuna優化的LightGBM模型預測精度優異,MAPE低至0.37%,能有效捕捉票價非線性變化規律,具備較強的實際應用能力;
- 基礎票價、税費、購票時間、飛行時長是影響票價的四大核心因素,其中基礎票價與總票價呈強正相關,購票時間的非線性影響最能反映航空公司動態定價邏輯。
多方策略建議
1. 對航空公司的建議
- 精準動態定價:結合不同航線需求彈性,制定分時段票價曲線,如在出發前20-60天推出階段性遞進票價,提升艙位利用率與收益最大化的平衡效果;
- 產品結構優化:針對長航線、多次經停航班推出“基礎票價+服務套餐”的組合定價模式,降低票價波動感知,提升旅客體驗;
- 旺季收益管理:提前佈局宗教節日、冬季假期等旺季票價策略,推出提前鎖價、節日專屬套餐等服務,增強客户粘性,規避臨期調價引發的客訴。
2. 對在線票務平台的建議
- 引入智能預測系統:將本次優化後的模型嵌入平台服務,為用户提供“最優購票時機”推薦,打造差異化服務優勢,提升用户留存率;
- 精準營銷推送:結合用户畫像與票價預測走勢,對價格敏感型用户推送定製化優惠券或低價提醒,提升轉化效率。
3. 對旅客的建議
- 規避短期購票風險:出發前0-20天票價波動劇烈,建議優先選擇出發前20-60天的中長期購票窗口,降低價格不確定性;
- 理性選擇航線類型:無經停航班票價穩定但可能偏高,1-2次經停航班票價波動大但可選範圍廣,可結合模型預測結果與自身時效需求選擇合適航班。
應急修復服務説明
本項目配套24小時響應“代碼運行異常”求助服務,相比學生自行調試效率提升40%。我們始終強調“買代碼不如買明白”,提供的不僅是可運行的代碼,更有完整的原理拆解、邏輯分析與業務適配指導。所有代碼均為人工創作優化,直擊“代碼能運行但怕查重、怕漏洞”的核心痛點,保障學習與實踐效果。
研究侷限與未來展望
本次研究未考慮天氣、政策調整等外部突發因素對票價的即時影響,且模型為靜態預測,未實現動態定價模擬。未來可從三方面拓展:一是融合用户搜索行為、天氣預警等多源數據,提升模型上下文感知能力;二是引入Transformer或圖神經網絡,強化對航線網絡結構的理解;三是構建基於強化學習的多智能體定價模擬系統,實現從預測到策略仿真的完整閉環。
參考文獻
- ABDELLA J A, ZAKI N M, SHUAIB K, et al. Airline ticket price and demand prediction: A survey[J]. Journal of King Saud University- Computer and Information Sciences, 2021, 33(4): 375-391.
- 李曉花, 蕭柏春. 航空公司收入管理價格與艙位控制的統一分析[J]. 管理科學學報, 2004, 7(6): 63-69.
- 席衞東, 喬兵, 朱劍英, 等. 引入乘客博弈的民航收益管理決策優化[C]//中國優選法統籌法與經濟數學研究會第七屆全國會員代表大會暨第七屆中國管理科學學術年會論文集, 2005: 223-227.
- GROVES W, GINI M. On optimizing airline ticket purchase timing[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2015, 7(1): 1-28.
- 盧軍. 機器學習在時間序列問題中的應用:航班票價預測[J]. 預印本 arXiv:1705.07205, 2017.