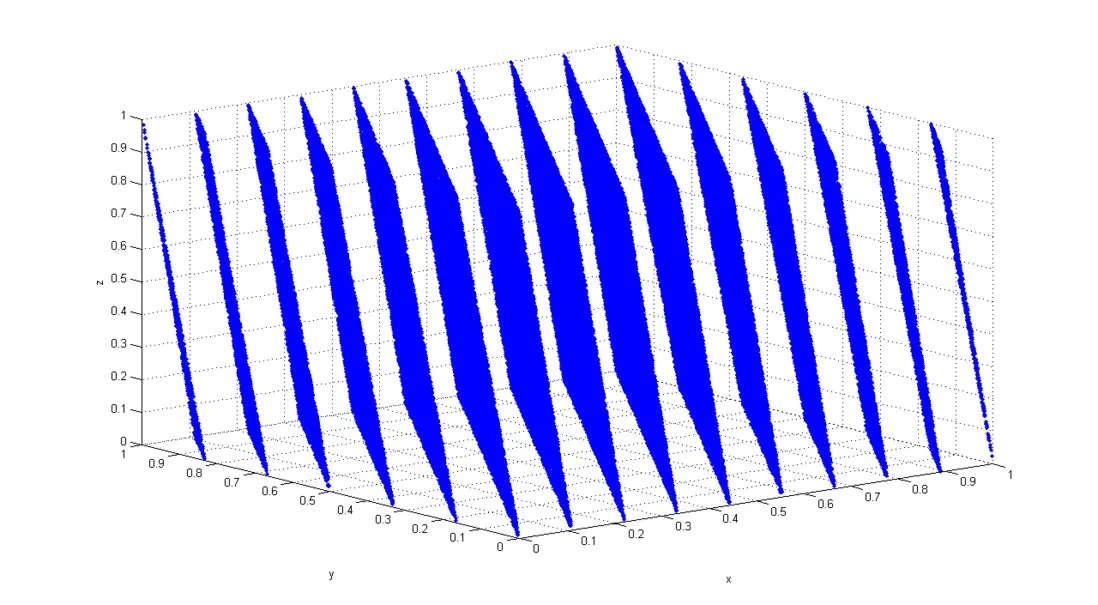
這是20世紀60年代IBM發明的RANDU偽隨機數生成算法的輸出值作三維可視化的樣子。用每三個連續輸出值為一個點座標,會清楚看到,這些點只規則的分佈在三維空間中的15個平面上!導致那時期很多用到此算法的論文結論都不可靠。
理想的偽隨機數生成點預期應該是均勻彌散在整個空間中。
RANDU算法是線性同餘生成器(LCG)一類的。
LCG優點是簡潔快速,有清晰的數學推導,可計算實現超長週期的滿週期參數。
但是,缺點是有連續值之間的序列相關性,造成內在晶格結構。當用於生成n維空間中的點,參數精心選擇得當,點就會分佈在高維空間的超平面上。參數選擇不當,就會像RANDU那樣在低維空間的平面上就聚集了。
直接用LCG的輸出值是無法通過重重隨機數統計檢驗的,
但是,給輸出加個混淆層,就大大改善了輸出的統計質量,可以通過一系列隨機數統計檢驗。這就是著名偽隨機數生成器PCG算法的原理——LCG+混淆。
非線性的二次同餘(QCG)、三次同餘(CCG)優缺點基本和LCG一致。
逆同餘生成器(ICG)是沒有明顯晶格結構的,可以直接輕易通過很高維度的統計檢驗。很適合於金融市場數據模擬等這些高維應用。
見 5.4.3 Inversive Generators
但是,ICG也存在同餘類生成器都有的長週期相關現象這個問題。讓生成器週期遠大於應用需要的週期,長週期相關缺點就不是問題了。
Python random庫用的偽隨機數生成算法是“Mersenne Twister”(MT)。這算法因其超長週期而被較多采用。
但是,MT這算法通不過一些隨機數統計檢驗(TestU01套件)。算法內部擴散性差,01不均衡。對於需要獨立隨機數生成器的蒙特卡羅模擬來説,使用MT只在種子值(而不是其他參數)上有差異的多個實例通常並不合適。
我測試整理出能通過多種隨機數統計檢驗套件的PRNG算法,如下:
| 算法 | 週期 |
|---|---|
| Quadratic Congruential Generator(QCG)+混淆 | 2^256(缺省) |
| Cubic Congruential Generator(CCG)+混淆 | 2^256(缺省) |
| Inversive Congruential Generator(ICG) | 102*2^256 |
| PCG64_XSL_RR | 2^128 |
| PCG64_DXSM | 2^128 |
| LCG64_32_ext | 2^128 |
| LCG128Mix_XSL_RR | 2^128 |
| LCG128Mix_DXSM | 2^128 |
| LCG128Mix_MURMUR3 | 2^128 |
| PhiloxCounter | 4*2^(4*64) |
| ThreeFryCounter | 4*2^(4*64) |
| AESCounter | 2^128 |
| ChaChaCounter | 2^128 |
| SPECKCounter | 2^129 |
| XSM64 | 2^128 |
| EFIIX64 | 2^64 |
| SplitMix64 | 2^64 |
| Ran64 | 2^64 |
然後實現了內含這些算法的偽隨機數生成器Py庫
源碼放在GitHub上,
https://github.com/fsssosei/P...
已經發布到了PyPI上,可以很方便的安裝分發:
pip install pure-prng
導入
from pure_prng_package import pure_prng
很簡單可以用起來,默認用的PRNG算法是CCG
>>> seed = 170141183460469231731687303715884105727 #隨意寫的種子值
>>> prng_instance = pure_prng(seed)
>>> source_random_number = prng_instance.source_random_number()
>>> next(source_random_number)
65852230656997158461166665751696465914198450243194923777324019418213544382100
QCG、CCG和LCG64_32_ext這三種是可變週期算法
>>> prng_instance = pure_prng(seed, new_prng_period = 2 ** 512)
>>> source_random_number = prng_instance.source_random_number()
>>> next(source_random_number)
8375486648769878807557228126183349922765245383564825377649864304632902242469125910865615742661048315918259479944116325466004411700005484642554244082978452
其他PRNG算法是固定週期算法
但是,庫中有method可設置輸出隨機數序列的週期(不論哪種PRNG算法生成的隨機數)
>>> period = 115792089237316195423570985008687907853269984665640564039457584007913129639747 #隨意寫的週期
>>> prng_instance = pure_prng(seed)
>>> rand_with_period = prng_instance.rand_with_period(period)
>>> next(rand_with_period)
mpz(65852230656997158461166665751696465914198450243194923777324019418213544381986)
庫中還有method生成任意精度浮點隨機數
>>> seed = 170141183460469231731687303715884105727
>>> prng_instance = pure_prng(seed)
>>> rand_float = prng_instance.rand_float(100)
>>> next(rand_float)
mpfr('0.56576176351048513846261940831522',100)

