題⽬描述

給⼀個鏈表，若其中包含環，請找出該鏈表的環的⼊⼝結點，否則，輸出null 。

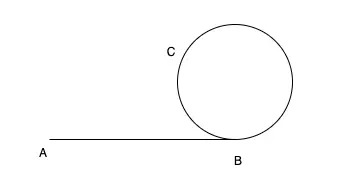
例如，輸⼊{1,2},{3,4,5} 時，對應的環形鏈表如下圖所示：

可以看到環的⼊⼝結點的結點值為3，所以返回結點值為3的結點。

給定的鏈表節點的結構：

public class ListNode {
    int val;
    ListNode next = null;
    ListNode(int val) {
        this.val = val;
    }
}

思路及解答

借用HashSet

直接使⽤ HashSet ,歷鏈表的時候，如果 HashSet 中不包含，則添加到 HashSet 中，如果鏈表中包含，説明已經回到環的第⼀個節點。Java 代碼實現如下：

public ListNode EntryNodeOfLoop(ListNode pHead) {
    HashSet set = new HashSet();
    while(pHead!=null){
        if(set.contains(pHead)){
            return pHead;
        }else{
            set.add(pHead);
            pHead = pHead.next;
        }
    }
    return null;
}

• 時間複雜度：O(n) - 每個節點最多訪問一次
• 空間複雜度：O(n) - 最壞情況下需要存儲所有節點

雙指針

上⾯的做法時間複雜度為O(n) ，由於藉助了⼀個hashSet ，空間複雜度也為O(n) 。那假設我們不需要使⽤額外的空間呢？怎麼做呢？

使⽤快慢雙指針，⼀個⼀次⾛⼀步，⼀個⼀次⾛兩步，當兩個重合在⼀起的時候，這時候，並不是環的⼊⼝節點。只能説明兩個指針，⼀個⽐另外⼀個多⾛了若⼲圈，可能是⼀圈，可能是2 ， 3 圈。

⽐如上⾯的，如果開始節點是A ，環的⼊⼝是B ，相遇的節點是C ，那麼

• 慢指針⾛的距離是： S=AB+BC
• 快指針⾛的距離是： 假設多⾛了n圈，2S = AB+(BC+CB)*n+BC ，

即 2(AB+BC) = AB+(BC+CB)*n+BC，也就是AB+BC = (BC+CB)*n

假設n =1 ，那麼AB = CB ,也就是當前位置到環的⼊⼝的⻓度，等於鏈表頭到環的⼊⼝的位置。

因此相遇之後，我們將⼀個快指針移動到鏈表頭，兩個指針每次⼀步，直到相遇，這個時候，相遇的節點就是環的⼊⼝節點。

public ListNode EntryNodeOfLoop(ListNode pHead) {
    ListNode quick = pHead;
    ListNode slow = pHead;
    while (quick != null && slow.next != null) {
        quick = quick.next;
        slow = slow.next.next;
        if (quick == slow) {
            quick = pHead;
            while (quick != slow) {
                quick = quick.next;
                slow = slow.next;
            }
            return quick;
        }
    }
    return null;
}

• 時間複雜度： O(n)
• 空間複雜度： O(1)

標記法（破壞性解法）

通過修改節點結構來標記已訪問的節點，適合可以修改鏈表的情況

public class Solution {

    public ListNode detectCycle(ListNode head) {
        if (head == null) return null;
        
        // 使用特殊值標記已訪問節點
        final int MARKER = Integer.MIN_VALUE;
        ListNode current = head;
        
        while (current != null) {
            // 如果遇到標記值，説明是環的入口
            if (current.val == MARKER) {
                // 恢復原始值（可選）
                return current;
            }
            // 標記當前節點
            current.val = MARKER;
            current = current.next;
        }
        
        return null;
    }
    
    /**
     * 替代方案：使用額外字段進行標記（如果節點結構可擴展）
     */
    static class MarkableListNode {
        int val;
        MarkableListNode next;
        boolean visited;
        
        MarkableListNode(int val) {
            this.val = val;
            this.visited = false;
        }
    }
}

• 時間複雜度：O(n) - 線性遍歷
• 空間複雜度：O(1) - 但破壞了鏈表結構