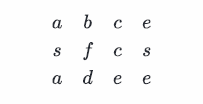題目描述

請設計⼀個函數，⽤來判斷在⼀個矩陣中是否存在⼀條包含某字符串所有字符的路徑。路徑可以從矩陣中的任意⼀個格⼦開始，每⼀步可以在矩陣中向左，向右，向上，向下移動⼀個格⼦。如果⼀條路徑經過了矩陣中的某⼀個格⼦，則該路徑不能再進⼊該格⼦。 例如矩陣：

中包含⼀條字符串 " bcced " 的路徑，但是矩陣中不包含 " abcb " 路徑，因為字符串的第⼀個字符 b佔據了矩陣中的第⼀⾏第⼆個格⼦之後，路徑不能再次進⼊該格⼦。

示例1

輸⼊：[[a,b,c,e],[s,f,c,s],[a,d,e,e]],"abcced"
返回值：true

思路及解答

DFS回溯

主要的思路是對於每⼀個字符為起點，遞歸向四周拓展，然後遇到不匹配返回 false ，匹配則接着匹配直到完成，⾥⾯包含了 回溯 的思想。步驟如下：

針對每⼀個字符為起點，初始化⼀個和矩陣⼀樣⼤⼩的標識數組，標識該位置是否被訪問過，⼀開始默認是false 。

1. 如果當前的字符索引已經超過了字符串⻓度，説明前⾯已經完全匹配成功，直接返回 true
2. 如果⾏索引和列索引，不在有效的範圍內，或者改位置已經標識被訪問，直接返回 false
3. 否則將當前標識置為已經訪問過
4. 如果矩陣當前位置的字符和字符串相等，那麼就字符串的索引加⼀，遞歸判斷周邊的四個，只要⼀個的結果為 true ，就返回 true ，否則將該位置置為沒有訪問過（相當於回溯，退回上⼀步），返回 false 。矩陣當前位置的字符和字符串不相等，否則同樣也是將該位置置為沒有訪問過（相當於回溯，退回上⼀步），返回 false 。

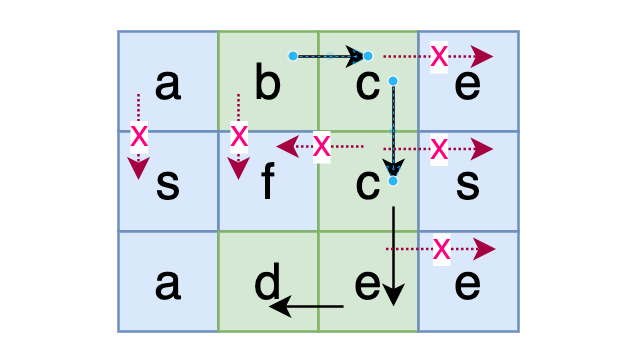
⽐如查找 bcced :

public class Solution {
    public boolean hasPath(char[][] matrix, String word) {
        // write code here
        if (matrix == null || word == null || word.length() == 0) {
        	return false;
        }
        
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                boolean[][] flags = new boolean[matrix.length][matrix[0].length];
                
                boolean result = judge(i, j, matrix, flags, word, 0);
                if (result) {
                	return true;
                }
            }
        }
        return false;
   }
    
   public boolean judge(int i, int j, char[][] matrix, boolean[][] flags, String words, int index) {
        if (index >= words.length()) {
        	return true;
        }
       
        if (i < 0 || j < 0 || i >= matrix.length || j >= matrix[0].length || flags[i][j]) {
        	return false;
        }
        flags[i][j] = true;
        
        if (matrix[i][j] == words.charAt(index)) {
            if (judge(i - 1, j, matrix, flags, words, index + 1)
            || judge(i + 1, j, matrix, flags, words, index + 1)
            || judge(i, j + 1, matrix, flags, words, index + 1)
            || judge(i, j - 1, matrix, flags, words, index + 1)) {
            	return true;
            } else {
                flags[i][j] = false;
                return false;
        	}
        } else {
            flags[i][j] = false;
            return false;
        }
    }
}

• 時間複雜度：O(3^k × m × n)，其中k為單詞長度，m、n為矩陣尺寸。每個點有3個方向可選（不能回退）
• 空間複雜度：O(k)，遞歸棧深度和visited數組空間

方向數組優化

使用額外的訪問標記數組來記錄路徑狀態。

public class Solution {
    public boolean exist(char[][] board, String word) {
        if (board == null || board.length == 0 || board[0].length == 0 || word == null) {
            return false;
        }
        
        int m = board.length, n = board[0].length;
        boolean[][] visited = new boolean[m][n];
        char[] words = word.toCharArray();
        
        // 遍歷矩陣中的每個單元格作為起始點
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (dfs(board, visited, words, i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    private boolean dfs(char[][] board, boolean[][] visited, char[] word, int i, int j, int index) {
        // 終止條件1：找到完整路徑
        if (index == word.length) {
            return true;
        }
        
        // 終止條件2：越界或已訪問或字符不匹配
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || 
            visited[i][j] || board[i][j] != word[index]) {
            return false;
        }
        
        // 標記當前單元格為已訪問
        visited[i][j] = true;
        
        // 向四個方向進行DFS搜索
        boolean found = dfs(board, visited, word, i + 1, j, index + 1) ||  // 向下
                       dfs(board, visited, word, i - 1, j, index + 1) ||  // 向上
                       dfs(board, visited, word, i, j + 1, index + 1) ||  // 向右
                       dfs(board, visited, word, i, j - 1, index + 1);    // 向左
        
        // 回溯：恢復訪問狀態
        visited[i][j] = false;
        
        return found;
    }
}

• 時間複雜度：O(3^k × m × n)，其中k為單詞長度，m、n為矩陣尺寸。每個點有3個方向可選（不能回退）
• 空間複雜度：O(k)，遞歸棧深度和visited數組空間

時間空間複雜度與方法一相同，但代碼更易擴展（如需要八方向移動時只需修改DIRECTIONS數組）

原地標記優化（最優）

通過修改原矩陣來標記訪問狀態，節省空間。

public class Solution {
    public boolean exist(char[][] board, String word) {
        if (board == null || board.length == 0 || word == null || word.length() == 0) {
            return false;
        }
        
        char[] words = word.toCharArray();
        
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (dfsOptimized(board, words, i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    private boolean dfsOptimized(char[][] board, char[] word, int i, int j, int index) {
        // 邊界檢查和字符匹配檢查
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || 
            board[i][j] != word[index]) {
            return false;
        }
        
        // 找到完整路徑
        if (index == word.length - 1) {
            return true;
        }
        
        // 原地標記：將當前字符臨時替換為特殊標記（不能出現的字符）
        char temp = board[i][j];
        board[i][j] = '#';  // 標記為已訪問
        
        // 四個方向搜索
        boolean res = dfsOptimized(board, word, i + 1, j, index + 1) ||
                     dfsOptimized(board, word, i - 1, j, index + 1) ||
                     dfsOptimized(board, word, i, j + 1, index + 1) ||
                     dfsOptimized(board, word, i, j - 1, index + 1);
        
        // 回溯：恢復原始字符
        board[i][j] = temp;
        
        return res;
    }
}

關鍵技巧：

1. 臨時修改：將訪問過的board[i][j]改為'#'（或其他不在字母表中的字符）
2. 自動避障：後續搜索遇到'#'會因字符不匹配而自動跳過
3. 狀態恢復：回溯時恢復原始字符，確保不影響其他路徑搜索

算法分析：

• 時間複雜度：O(3^k × m × n)，與前述方法相同
• 空間複雜度：O(1)，顯著優化！僅使用常數空間（遞歸棧空間不可避免）