題⽬描述

輸⼊⼀個⻓度為 n 整數數組，數組⾥⾯可能含有相同的元素，實現⼀個函數來調整該數組中數字的順序，使得所有的奇數位於數組的前⾯部分，所有的偶數位於數組的後⾯部分，對奇數和奇數，偶數和偶數之間的相對位置不做要求，但是時間複雜度和空間複雜度必須如下要求。

數據範圍：0 ≤ n ≤ 50000，數組中每個數的值 0 ≤ val ≤ 10000

要求：時間複雜度 O(n)，空間複雜度 O(1)

示例 1
輸⼊：[1,2,3,4]
返回值：[1,3,2,4]
説明：[3,1,2,4]或者[3,1,4,2]也是正確答案

示例 2
輸⼊：[1,3,5,6,7]
返回值：[1,3,5,7,6]
説明：[3,1,5,7,6]等也是正確答案

思路及解答

兩次遍歷

第一次遍歷收集奇數，第二次遍歷收集偶數

這種方法雖然簡單易懂，但需要額外空間，不符合題目要求

public class Solution {
    public int[] reorderArray(int[] nums) {
        if (nums == null || nums.length == 0) {
            return new int[0];
        }
        
        int[] result = new int[nums.length];
        int index = 0;
        
        // 第一次遍歷：收集所有奇數
        for (int num : nums) {
            if (num % 2 == 1) {
                result[index++] = num;
            }
        }
        
        // 第二次遍歷：收集所有偶數
        for (int num : nums) {
            if (num % 2 == 0) {
                result[index++] = num;
            }
        }
        
        return result;
    }
}

• 時間複雜度：O(n)
• 空間複雜度：O(n)

雙指針交換（推薦）

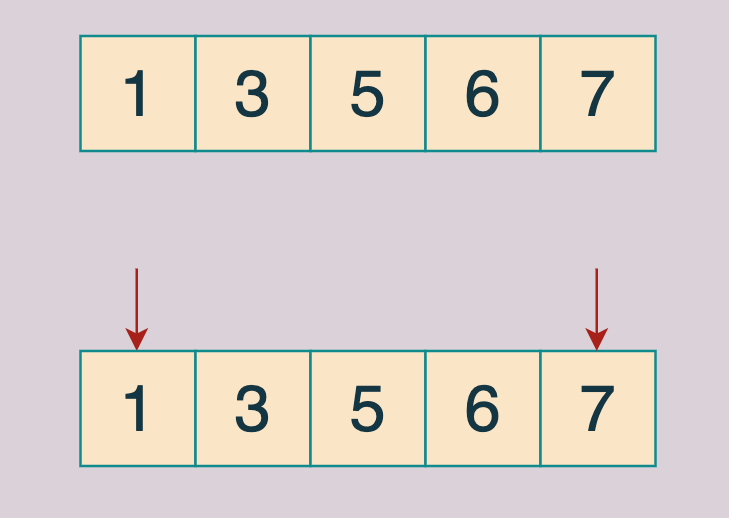
這道題需要奇數在⼀半，偶數在另外⼀半就可以，並沒有要求他們之間的順序，那麼就可以⽤雙指針，⼀個指針在左邊，⼀個指針在右邊，⽐如 1,3,5,6,7 :

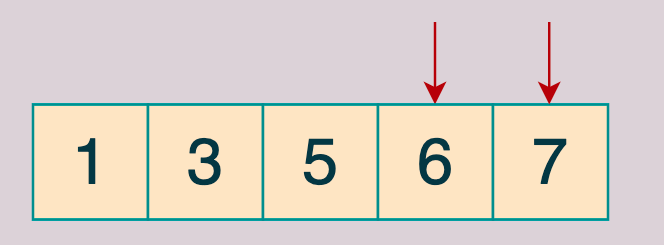
左指針往右遍歷直到找到偶數，也就是 6 停下來，

右指針往左⾛，直到找到第⼀個奇數，也就是 7 停下來。

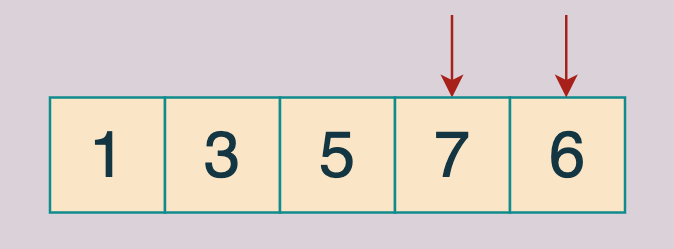
兩者交換:

左指針繼續往右邊⾛，兩個指針相遇，結束，這個時候其實偶數已經全部在右邊了。

這個例⼦⾥⾯只經過⼀次交換，如果是多次交換，那麼結束的條件同樣也是兩個指針相遇。

public class Solution {
    public int[] reorderArray(int[] nums) {
        if (nums == null || nums.length <= 1) {
            return nums;
        }
        
        int left = 0;                    // 左指針，從數組開頭開始
        int right = nums.length - 1;     // 右指針，從數組末尾開始
        
        while (left < right) {
            // 左指針向右移動，直到找到偶數
            while (left < right && nums[left] % 2 == 1) {
                left++;
            }
            
            // 右指針向左移動，直到找到奇數
            while (left < right && nums[right] % 2 == 0) {
                right--;
            }
            
            // 如果左指針仍在右指針左邊，交換奇偶數
            if (left < right) {
                int temp = nums[left];
                nums[left] = nums[right];
                nums[right] = temp;
                left++;
                right--;
            }
        }
        
        return nums;
    }
}

• 時間複雜度：O(n)，每個元素最多被訪問一次
• 空間複雜度：O(1)，只使用了常數級別的額外空間