題目描述

地上有⼀個 m ⾏和 n 列的⽅格。⼀個機器⼈從座標（0,0） 的格⼦開始移動，每⼀次只能向左，右，上，下四個⽅向移動⼀格，但是不能進⼊⾏座標和列座標的數位之和⼤於 k 的格⼦。 例如，當k 為 18 時，機器⼈能夠進⼊⽅格（35,37） ，因為 3+5+3+7 = 18 。但是，它不能進⼊⽅格（35,38） ，因為 3+5+3+8 = 19 。請問該機器⼈能夠達到多少個格⼦？

示例1

輸⼊：5,10,10
返回值：21

示例2

輸⼊：10,1,100
返回值：29

説明：[0,0],[0,1],[0,2],[0,3],[0,4],[0,5],[0,6],[0,7],[0,8],[0,9],[0,10],[0,11],[0,12],[0,13],[0,14],[0,15],[0,16],[0,17],[0,18],[0,19],[0,20],[0,21],[0,22],[0,23],[0,24],[0,25],[0,26],[0,27],[0,28] 這29種，後⾯的[0,29] , [0,30] 以及[0,31] 等等是⽆法到達的。

思路及解答

DFS（深度優先搜索）

深度優先搜索算法，也就是 DFS ,⾸先需要初始化數組，注意是 boolean 類型的⼆元數組。邊初始化
邊計算位數的和，判斷如果⼤於等於閾值的話，就直接置為 true ，也就是已經被訪問到（但是這⼀部分計⼊結果）。

然後遍歷每⼀個元素，只要 i ， j 不在合法的索引範圍或者是已經被訪問過，都會直接返回
false 。

否則的話，可訪問的數量 +1 ，並且遞歸遍歷上下左右四個元素，返回最終的可訪問的個數。

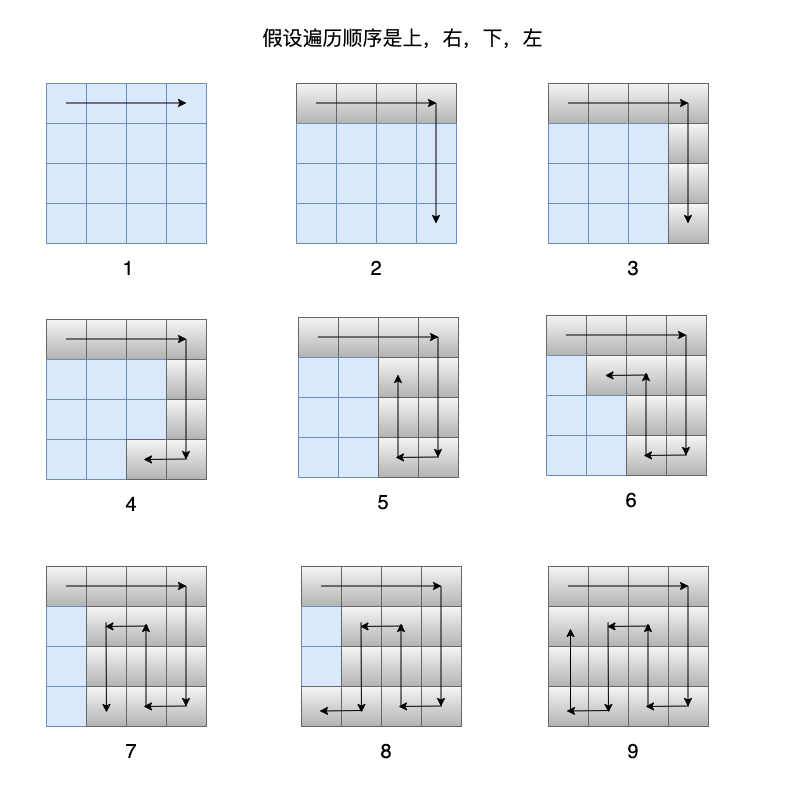
DFS 會優先同⼀個⽅向，⼀直⾛下去，不撞南牆不回頭，直到條件不滿⾜的時候，才會回頭。回頭之後，每次只會回頭⼀步，往另外⼀個⽅向去，同樣是⼀頭扎進去。

假設有⼀個 4 x 4 的⽅格，從第⼀個開始遍歷，假設遍歷順序是上，右，下，左，那麼遍歷的順序如下：

public class Solution {
    public int movingCount(int threshold, int rows, int cols) {
        if (rows > 0 && cols > 0) {
            boolean[][] visited = new boolean[rows][cols];
            for (int i = 0; i < rows; i++) {
                for (int j = 0; j < cols; j++) {
                    // 如果⼤於閾值，設置已被訪問過
                    visited[i][j] = ((getSum(i) + getSum(j)) > threshold);
                }
            }
            return getNum(visited, 0, 0, 0);
        }
        return 0;
    }
    
   // 獲取可以被訪問的個數
   private int getNum(boolean[][] visited, int i, int j, int count) {
        if (i < 0 || j < 0 || i >= visited.length || j >= visited[0].length ||
            visited[i][j]) {
            return count;
        }
        count++;
        visited[i][j] = true;
        count = getNum(visited, i, j + 1, count);
        count = getNum(visited, i, j - 1, count);
        count = getNum(visited, i + 1, j, count);
        count = getNum(visited, i - 1, j, count);
        return count;
   }
   
    // 計算位數之和
   private int getSum(int num) {
        int result = 0;
        while (num > 0) {
            result = result + num % 10;
            num = num / 10;
        }
        return result;
    }
}

• 時間複雜度：最壞的情況是將所有的格⼦都遍歷⼀遍， O(m*n) 。
• 空間複雜度：藉助了額外的空間保存是否被訪問過，同樣為O(m*n) 。

BFS（⼴度優先搜索）

⼴度優先搜索，也就是沒進⾏⼀步，優先搜索當前點的各個⽅向上的點，不急着往下搜索，等搜索完當前點的各個⽅向的點，再依次把之前搜索的點，取出來，同樣先搜索周邊的點...

這樣直到所有都被搜索完成。

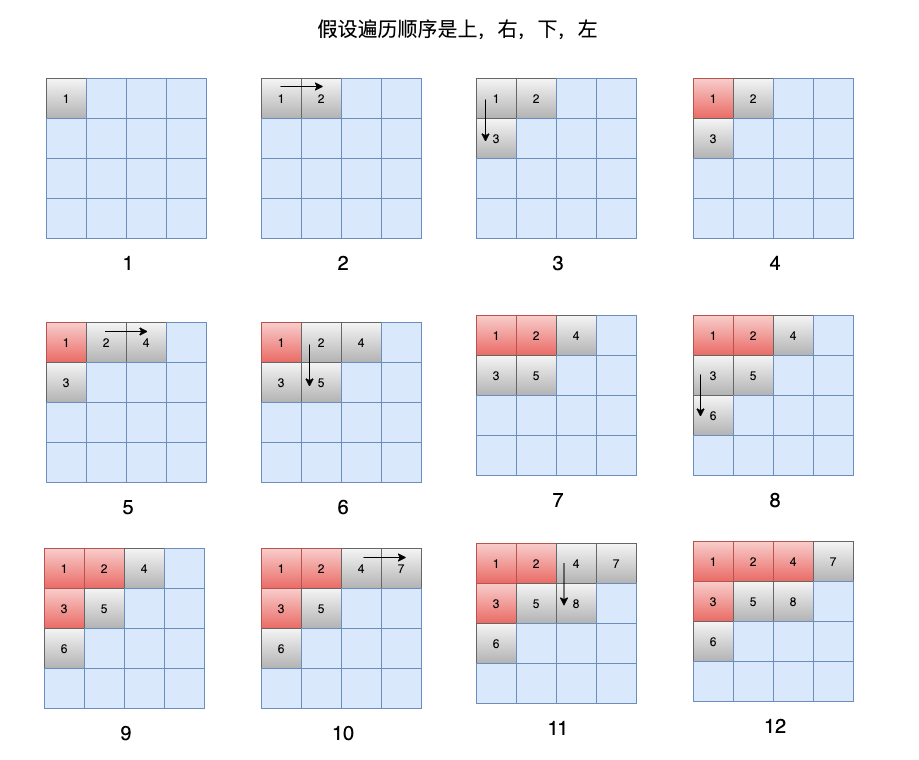
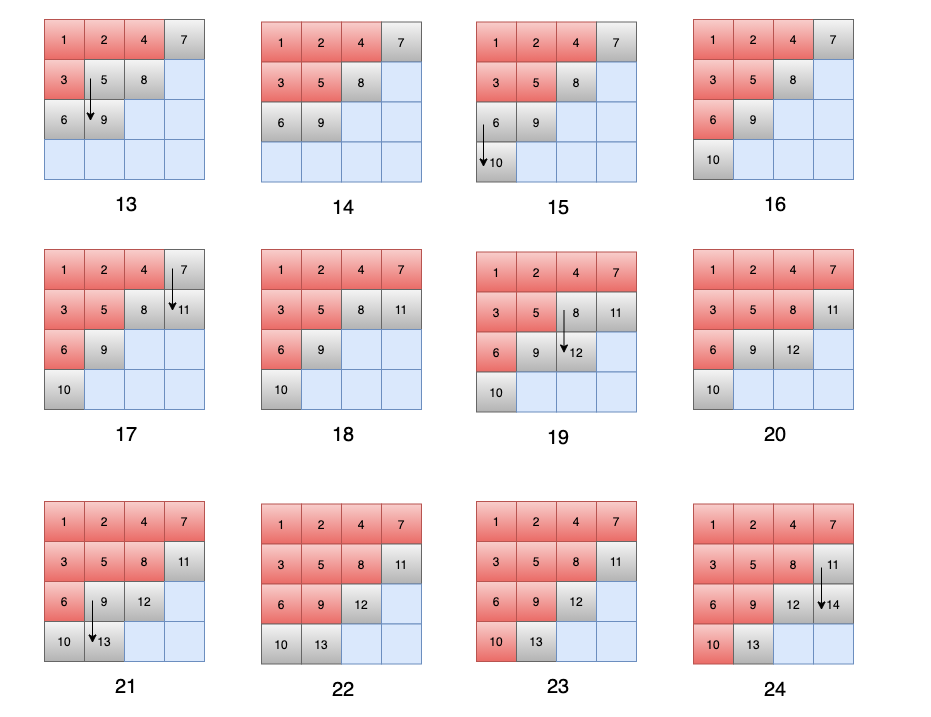
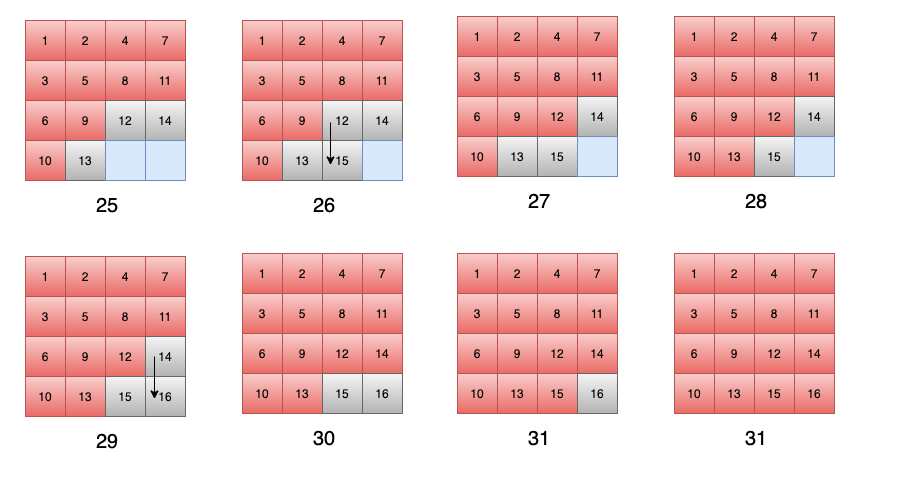
同樣有⼀個 4 x 4 的⽅格，從第⼀個開始遍歷，假設遍歷順序是上，右，下，左，那麼遍歷的順序如下：

在上⾯的過程圖示中，我們可以發現，訪問是有順序的，每遍歷⼀個新的⽅塊，都會標⼀個順序，然後按照順序遍歷其四個⽅向。

這也就是⼴度優先搜索的本質，我們需要⼀個隊列，來保存遍歷的順序，每次都從隊列⾥⾯取出⼀個位置，遍歷其四周的⽅塊，每次遍歷到的點，都會放到隊列⾥⾯，這樣直到隊列為空的時候，也就是全部遍歷完成。

import java.util.LinkedList;
import java.util.Queue;

public class Solution13 {
    public int movingCount(int threshold, int rows, int cols) {
        boolean[][] visited = new boolean[rows][cols];
        int count = 0;
        
        Queue<int[]> queue = new LinkedList<>();
        // 把第⼀個點加到隊列⾥⾯
        queue.add(new int[]{0, 0});
        
        while (queue.size() > 0) {
            // ⼀直取數據，直到隊列為空
            int[] x = queue.poll();
            // 取出來的數據，包含x，y座標
            int i = x[0], j = x[1];
            // 如果訪問過或者不符合，直接下⼀個
            if (i >= rows || j >= cols || threshold < getSum(i) + getSum(j) || visited[i][j]) continue;
            
            // 置為訪問過
            visited[i][j] = true;
            // 數量增加
            count++;
            // 右
            queue.add(new int[]{i + 1, j});
            // 下
            queue.add(new int[]{i, j + 1});
       }
       return count;
   }
   
    // 計算位數之和
   private int getSum(int num) {
        int result = 0;
        while (num > 0) {
            result = result + num % 10;
            num = num / 10;
        }
        return result;
    }
}

• 時間複雜度：最壞的情況是將所有的格⼦都遍歷⼀遍， O(m*n) 。
• 空間複雜度：藉助了額外的空間保存是否被訪問過，同樣為O(m*n) 。

動態規劃（最優解）

利用遞推關係式，避免重複計算。

• 格子(i,j)可達 ⇔ 數位和滿足條件 ∧ (左邊格子可達 ∨ 上邊格子可達)
• dp[i][j]表示(i,j)是否可達，基於左邊和上邊格子的狀態：dp[i][j] = (digitSum(i) + digitSum(j) ≤ k) && (dp[i-1][j] || dp[i][j-1])

public class Solution {
    public int movingCount(int m, int n, int k) {
        if (k == 0) return 1;
        
        // dp[i][j]表示格子(i,j)是否可達
        boolean[][] dp = new boolean[m][n];
        dp[0][0] = true;  // 起點可達
        int count = 1;     // 起點已計入
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 跳過起點和數位和超限的情況
                if ((i == 0 && j == 0) || digitSum(i) + digitSum(j) > k) {
                    continue;
                }
                
                // 檢查是否可以從左邊或上邊到達當前格子
                if (i - 1 >= 0) {
                    dp[i][j] |= dp[i - 1][j];  // 從上邊來
                }
                if (j - 1 >= 0) {
                    dp[i][j] |= dp[i][j - 1];  // 從左邊來
                }
                
                // 如果當前格子可達，計數加1
                count += dp[i][j] ? 1 : 0;
            }
        }
        
        return count;
    }
    
    private int digitSum(int num) {
        int sum = 0;
        while (num > 0) {
            sum += num % 10;
            num /= 10;
        }
        return sum;
    }
}

• 時間複雜度：O(mn)，雙重循環遍歷所有格子
• 空間複雜度：O(mn)，dp數組的空間