題⽬描述

有⼀種將字⺟編碼成數字的⽅式：'a'->1, 'b->2', ... , 'z->26'。

現在給⼀串數字，返回有多少種可能的譯碼結果

示例1
輸⼊："12"
返回值：2
説明：2種可能的譯碼結果（”ab” 或”l”）

示例2
輸⼊："31717126241541717"
返回值：192
説明：192種可能的譯碼結果

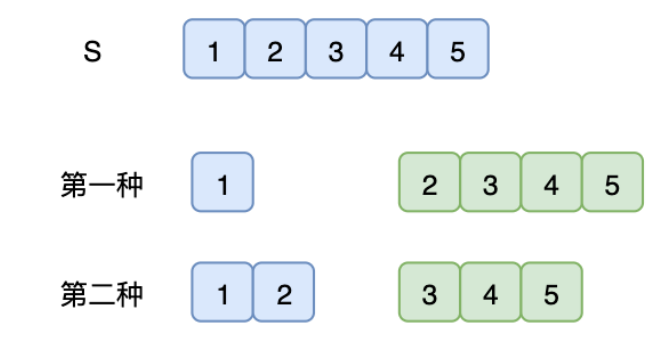
仔細觀察，就會發現上⾯的編碼從 1 到 26，也就是可能⼀次譯碼使⽤是 1 位，也可能是⼀次譯碼⽤了 2位，⽐如 12 ，可以第⼀次⽤ 1，2 分開分別譯碼，也可以把 1，2 合併起來進⾏譯碼。

思路及解法

暴力遞歸

假設⼀個字符是S，第⼀次拆解就有兩種情況，然後分別對後⾯的部分分別譯碼，使⽤遞歸即可：

public class Solution46 {
     public int solve (String nums) {
     	return recursion(nums.toCharArray(), 0);
     }
    
     public int recursion(char[] nums, int start){
         if(start == nums.length){
         	return 1;
         }
         
         if(nums[start] == '0')
         	return 0;
         
         // 使⽤⼀位字符譯碼
         int count1 = recursion(nums,start+1);
         int count2 = 0;
         // 符合兩位字符的譯碼
         if((start < nums.length-1) && (nums[start] == '1' || (nums[start] == '2' &&nums[start+1] <= '6'))){
         	count2 = recursion(nums,start+2);
         }
         return count1 + count2;
     }
}

但是上⾯的代碼時間複雜度太⾼了，只要字符稍微⻓⼀點，運⾏時間就容易超過限制了：

記憶化遞歸

為了避免重複計算子問題，我們使用一個備忘錄（memo）來存儲已經計算過的結果。

class Solution {
    public int numDecodings(String s) {
        if (s == null || s.length() == 0) return 0;
        // 備忘錄，初始化為-1表示未計算
        Integer[] memo = new Integer[s.length()];
        return dfs(s, 0, memo);
    }
    
    private int dfs(String s, int index, Integer[] memo) {
        // 基準情況1：成功解碼到末尾，算作一種有效方法
        if (index == s.length()) {
            return 1;
        }
        // 基準情況2：當前字符是'0'，無法解碼，此路徑無效
        if (s.charAt(index) == '0') {
            return 0;
        }
        // 如果當前子問題已經計算過，直接返回結果
        if (memo[index] != null) {
            return memo[index];
        }
        
        int ways = 0;
        // 選擇1：解碼當前1位數字
        ways += dfs(s, index + 1, memo);
        
        // 選擇2：如果存在下一位，並且當前兩位數字在10-26之間，則解碼當前2位數字
        if (index + 1 < s.length()) {
            int twoDigits = (s.charAt(index) - '0') * 10 + (s.charAt(index + 1) - '0');
            if (twoDigits >= 10 && twoDigits <= 26) {
                ways += dfs(s, index + 2, memo);
            }
        }
        
        // 將結果存入備忘錄
        memo[index] = ways;
        return ways;
    }
}

• 時間複雜度：O(n)，每個子問題最多被計算一次。
• 空間複雜度：O(n)，遞歸棧的深度和備忘錄的空間

動態規劃

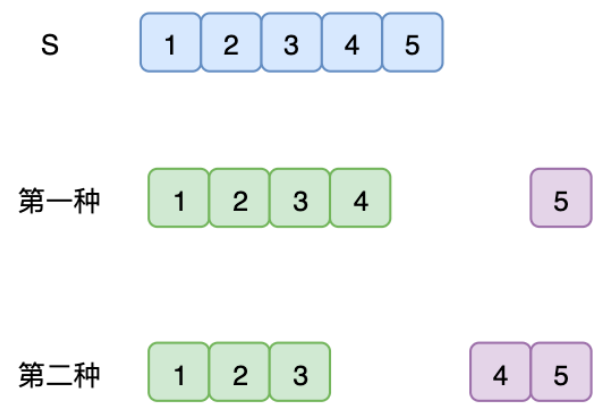
將過程逆推，要想求得當前的字符串的譯碼類型，其實有兩種，最後⼀個單獨翻譯，另外⼀種是倒數最後兩個字符合起來翻譯，這兩者之和就是我們所要求的結果。

⽽要求前⾯的值，需要求更前⾯的值，最後⼀定會求得⼀個字符和兩個字符的結果。其實這就是動態規劃⾥⾯説的狀態變化。遞歸其實就是逆推，這樣會導致很多重複的計算。動態規劃,則是從⼩數值計算到⼤數值。

既然我們知道是動態規劃，定義 dp[i] 為數字串從左到右第i個數字結尾的當前數字串所擁有的翻譯⽅法數，接着就需要找出狀態轉移⽅程：

• 如果 i=0 , dp[i]=1
• 否則
  • 如果nums[i]=0，説明需要和前⾯⼀個字符⼀起翻譯
    • 如果i == 1，以10或者20開頭， dp[i] = 1
    • 否則，數字串中存在10或者20的情況下，當前譯碼數等於後退兩步的譯碼數， dp[i] =dp[i-2];
  • 否則，在符合字符範圍內， dp[i]=dp[i-1]+dp[i-2]

class Solution {
    public int numDecodings(String s) {
        if (s == null || s.length() == 0 || s.charAt(0) == '0') {
            return 0; // 處理空串或以'0'開頭的無效情況
        }
        
        int n = s.length();
        int[] dp = new int[n + 1];
        // 初始化
        dp[0] = 1; // 空字符串有一種解碼方式（解碼為空）
        dp[1] = 1; // 第一個字符只要不是'0'（前面已判斷），就有1種解碼方式

        for (int i = 2; i <= n; i++) {
            int oneDigit = s.charAt(i - 1) - '0';  // 看最後一個字符（1位數字）
            int twoDigits = (s.charAt(i - 2) - '0') * 10 + oneDigit; // 看最後兩個字符（2位數字）

            // 情況1：最後一個字符可以單獨解碼（必須是1-9）
            if (oneDigit >= 1 && oneDigit <= 9) {
                dp[i] += dp[i - 1];
            }
            // 情況2：最後兩個字符可以組合解碼（必須是10-26）
            if (twoDigits >= 10 && twoDigits <= 26) {
                dp[i] += dp[i - 2];
            }
        }
        return dp[n];
    }
}

• 時間複雜度：O(n)，需要遍歷整個字符串一次。
• 空間複雜度：O(n)，用於存儲 dp數組。

空間優化動態規劃（推薦）

觀察上面的代碼可以發現，計算 dp[i]時只依賴於 dp[i-1]和 dp[i-2]。因此，我們可以不用維護整個數組，只用兩個變量來滾動記錄之前的狀態即可，從而將空間複雜度優化到常數級別。

class Solution {
    public int numDecodings(String s) {
        if (s == null || s.length() == 0 || s.charAt(0) == '0') {
            return 0;
        }
        
        int n = s.length();
        // 使用變量替代dp數組
        int prevPrev = 1; // 對應於 dp[i-2]，初始化為dp[0]=1
        int prev = 1;     // 對應於 dp[i-1]，初始化為dp[1]=1

        for (int i = 2; i <= n; i++) {
            int current = 0;
            int oneDigit = s.charAt(i - 1) - '0';
            int twoDigits = (s.charAt(i - 2) - '0') * 10 + oneDigit;

            // 情況1：單獨解碼最後一個字符
            if (oneDigit >= 1 && oneDigit <= 9) {
                current += prev; // 相當於 dp[i] += dp[i-1]
            }
            // 情況2：組合解碼最後兩個字符
            if (twoDigits >= 10 && twoDigits <= 26) {
                current += prevPrev; // 相當於 dp[i] += dp[i-2]
            }
            
            // 滾動更新變量，為下一次迭代做準備
            prevPrev = prev;
            prev = current;
        }
        return prev;
    }
}

• 時間複雜度：O(n)。
• 空間複雜度：O(1)，只使用了固定數量的變量