題⽬描述

假設你有⼀個數組 prices ，⻓度為 n ，其中 prices[i] 是股票在第 i 天的價格，請根據這個價格數組，返回買賣股票能獲得的最⼤收益

1. 你可以買⼊⼀次股票和賣出⼀次股票，並⾮每天都可以買⼊或賣出⼀次，總共只能買⼊和賣出⼀次，且買⼊必須在賣出的前⾯的某⼀天
2. 如果不能獲取到任何利潤，請返回 0
3. 假設買⼊賣出均⽆⼿續費

示例1：
輸⼊：[8,9,2,5,4,7,1]
返回值: 5
説明: 在第3天(股票價格 = 2)的時候買⼊，在第6天(股票價格 = 7)的時候賣出，最⼤利潤 = 7-2 = 5，不能選擇在第2天買⼊，第3天賣出，這樣就虧損7了；同時，你也不能在買⼊前賣出股票。

示例2：
輸⼊：[2,4,1]
返回值: 2

思路及解答

暴⼒窮舉

這⾥涉及的節點⽆⾮是買⼊，賣出，那麼我們遍歷所有的數據，作為買⼊⽇期，同時將該⽇期後⾯每⼀個都作為賣出⽇期來計算，只要維護最⼤的利潤即可。

public class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length < 2) {
            return 0;
        }
        
        int maxProfit = 0;
        int n = prices.length;
        
        // 外層循環：遍歷所有可能的買入點
        for (int i = 0; i < n - 1; i++) {
            // 內層循環：遍歷所有可能的賣出點（必須在買入點之後）
            for (int j = i + 1; j < n; j++) {
                int profit = prices[j] - prices[i];
                if (profit > maxProfit) {
                    maxProfit = profit;
                }
            }
        }
        
        return maxProfit;
    }
}

• 時間複雜度： O(n2)
• 空間複雜度：O(1)

貪⼼法（最優解）

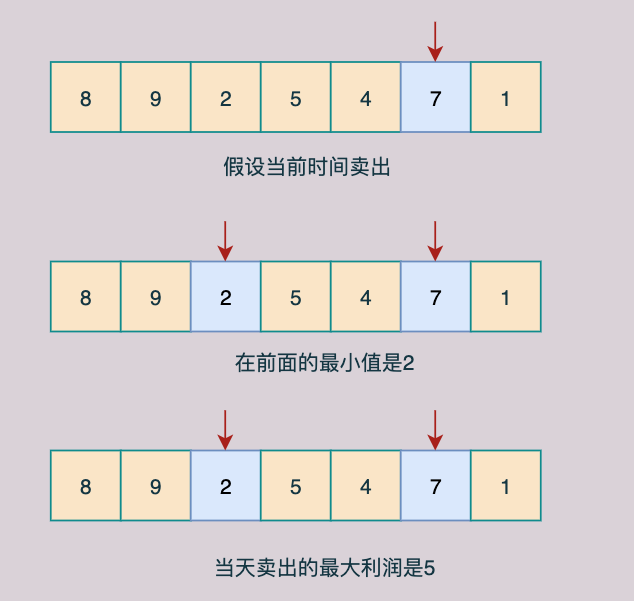
我們要想得到⼀個最⼤的利潤，其實就是要兩者差值最⼤。如果讓差值最⼤，假設在當天賣出，那麼什麼時候買⼊最好呢？

當然是在前⾯找到最⼩的買⼊點，⽐如：

⽽前⾯的最⼩值，其實我們在遍歷的時候是可以不斷維護的，所以我們只要遍歷⼀次數組即可。

關鍵思想：

• 最大利潤 = 某日價格 - 該日之前的最低價格
• 只需維護兩個變量：
  • minPrice：遍歷過程中遇到的最低價格
  • maxProfit：當前能獲得的最大利潤

public class Solution63 {
    public int maxProfit(int[] prices) {
        int min = Integer.MAX_VALUE;
        int result = 0;
        for (int value: prices) {
            // 維護最⼩值
            min = Math.min(min, value);
            // 當前值減去前⾯最⼩值，與利潤最⼤值對⽐，維護好利潤最⼤值
            result = Math.max(result, value - min);
        }
        return result;
    }
}

• 時間複雜度：O(n)，只需遍歷一次數組
• 空間複雜度：O(1)，只使用常數空間

執行過程示例（prices = [8,9,2,5,4,7,1]）

i=0: price=8, minPrice=8, maxProfit=0
i=1: price=9, minPrice=8, maxProfit=1
i=2: price=2, minPrice=2, maxProfit=1
i=3: price=5, minPrice=2, maxProfit=3
i=4: price=4, minPrice=2, maxProfit=3
i=5: price=7, minPrice=2, maxProfit=5
i=6: price=1, minPrice=1, maxProfit=5
結果：5

動態規劃

dp[i]表示前i天的最大利潤，狀態轉移基於前i-1天的結果

狀態定義：

• minPrice[i]：前i天的最低價格
• maxProfit[i]：前i天能獲得的最大利潤

public class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length < 2) {
            return 0;
        }
        
        int minPrice = prices[0];
        int maxProfit = 0;
        
        for (int i = 1; i < prices.length; i++) {
            // 狀態轉移方程：
            // 前i天的最大利潤 = max(前i-1天的最大利潤, 第i天價格-前i-1天的最低價格)
            maxProfit = Math.max(maxProfit, prices[i] - minPrice);
            minPrice = Math.min(minPrice, prices[i]);
        }
        
        return maxProfit;
    }
}

• 時間複雜度：O(n)，單次遍歷
• 空間複雜度：O(1)，優化後只需兩個變量