建圖函數

List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
    // 圖中共有 numCourses 個節點
    List<Integer>[] graph = new LinkedList[numCourses];
    for (int i = 0; i < numCourses; i++) {
        graph[i] = new LinkedList<>();
    }
    for (int[] edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 添加一條從 from 指向 to 的有向邊
        // 邊的方向是「被依賴」關係，即修完課程 from 才能修課程 to
        graph[from].add(to);
    }
    return graph;
}

環檢測算法

DFS

// 記錄一次遞歸堆棧中的節點
boolean[] onPath;
// 記錄遍歷過的節點，防止走回頭路
boolean[] visited;
// 記錄圖中是否有環
boolean hasCycle = false;

boolean canFinish(int numCourses, int[][] prerequisites) {
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);

    visited = new boolean[numCourses];
    onPath = new boolean[numCourses];

    for (int i = 0; i < numCourses; i++) {
        // 遍歷圖中的所有節點
        traverse(graph, i);
    }
    // 只要沒有循環依賴可以完成所有課程
    return !hasCycle;
}

void traverse(List<Integer>[] graph, int s) {
    if (onPath[s]) {
        // 出現環
        hasCycle = true;
    }

    if (visited[s] || hasCycle) {
        // 如果已經找到了環，也不用再遍歷了
        return;
    }
    // 前序代碼位置
    visited[s] = true;
    onPath[s] = true;
    for (int t : graph[s]) {
        traverse(graph, t);
    }
    // 後序代碼位置
    onPath[s] = false;
}

BFS

// 主函數
public boolean canFinish(int numCourses, int[][] prerequisites) {
    // 建圖，有向邊代表「被依賴」關係
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);
    // 構建入度數組
    int[] indgree = new int[numCourses];
    for (int[] edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 節點 to 的入度加一
        indgree[to]++;
    }

    // 根據入度初始化隊列中的節點
    Queue<Integer> q = new LinkedList<>();
    for (int i = 0; i < numCourses; i++) {
        if (indgree[i] == 0) {
            // 節點 i 沒有入度，即沒有依賴的節點
            // 可以作為拓撲排序的起點，加入隊列
            q.offer(i);
        }
    }

    // 記錄遍歷的節點個數
    int count = 0;
    // 開始執行 BFS 循環
    while (!q.isEmpty()) {
        // 彈出節點 cur，並將它指向的節點的入度減一
        int cur = q.poll();
        count++;
        for (int next : graph[cur]) {
            indgree[next]--;
            if (indgree[next] == 0) {
                // 如果入度變為 0，説明 next 依賴的節點都已被遍歷
                q.offer(next);
            }
        }
    }

    // 如果所有節點都被遍歷過，説明不成環
    return count == numCourses;
}

這段 BFS 算法的思路：

1、構建鄰接表，和之前一樣，邊的方向表示「被依賴」關係。

2、構建一個 indegree 數組記錄每個節點的入度，即 indegree[i] 記錄節點 i 的入度。

3、對 BFS 隊列進行初始化，將入度為 0 的節點首先裝入隊列。

4、開始執行 BFS 循環，不斷彈出隊列中的節點，減少相鄰節點的入度，並將入度變為 0 的節點加入隊列。

5、如果最終所有節點都被遍歷過（count 等於節點數），則説明不存在環，反之則説明存在環。

拓撲排序算法

對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意一對頂點u和v，若邊(u,v)∈E(G)，則u在線性序列中出現在v之前。通常，這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列，簡稱拓撲序列。簡單的説，由某個集合上的一個偏序得到該集合上的一個全序，這個操作稱之為拓撲排序。

DFS

// 記錄後序遍歷結果
List<Integer> postorder = new ArrayList<>();
// 記錄是否存在環
boolean hasCycle = false;
boolean[] visited, onPath;

// 主函數
public int[] findOrder(int numCourses, int[][] prerequisites) {
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);
    visited = new boolean[numCourses];
    onPath = new boolean[numCourses];
    // 遍歷圖
    for (int i = 0; i < numCourses; i++) {
        traverse(graph, i);
    }
    // 有環圖無法進行拓撲排序
    if (hasCycle) {
        return new int[]{};
    }
    // 逆後序遍歷結果即為拓撲排序結果
    Collections.reverse(postorder);
    int[] res = new int[numCourses];
    for (int i = 0; i < numCourses; i++) {
        res[i] = postorder.get(i);
    }
    return res;
}

// 圖遍歷函數
void traverse(List<Integer>[] graph, int s) {
    if (onPath[s]) {
        // 發現環
        hasCycle = true;
    }
    if (visited[s] || hasCycle) {
        return;
    }
    // 前序遍歷位置
    onPath[s] = true;
    visited[s] = true;
    for (int t : graph[s]) {
        traverse(graph, t);
    }
    // 後序遍歷位置
    postorder.add(s);
    onPath[s] = false;
}

BFS

// 主函數
public int[] findOrder(int numCourses, int[][] prerequisites) {
    // 建圖，和環檢測算法相同
    List<Integer>[] graph = buildGraph(numCourses, prerequisites);
    // 計算入度，和環檢測算法相同
    int[] indgree = new int[numCourses];
    for (int[] edge : prerequisites) {
        int from = edge[1], to = edge[0];
        indgree[to]++;
    }

    // 根據入度初始化隊列中的節點，和環檢測算法相同
    Queue<Integer> q = new LinkedList<>();
    for (int i = 0; i < numCourses; i++) {
        if (indgree[i] == 0) {
            q.offer(i);
        }
    }

    // 記錄拓撲排序結果
    int[] res = new int[numCourses];
    // 記錄遍歷節點的順序（索引）
    int count = 0;
    // 開始執行 BFS 算法
    while (!q.isEmpty()) {
        int cur = q.poll();
        // 彈出節點的順序即為拓撲排序結果
        res[count] = cur;
        count++;
        for (int next : graph[cur]) {
            indgree[next]--;
            if (indgree[next] == 0) {
                q.offer(next);
            }
        }
    }

    if (count != numCourses) {
        // 存在環，拓撲排序不存在
        return new int[]{};
    }

    return res;
}

二分圖判定算法

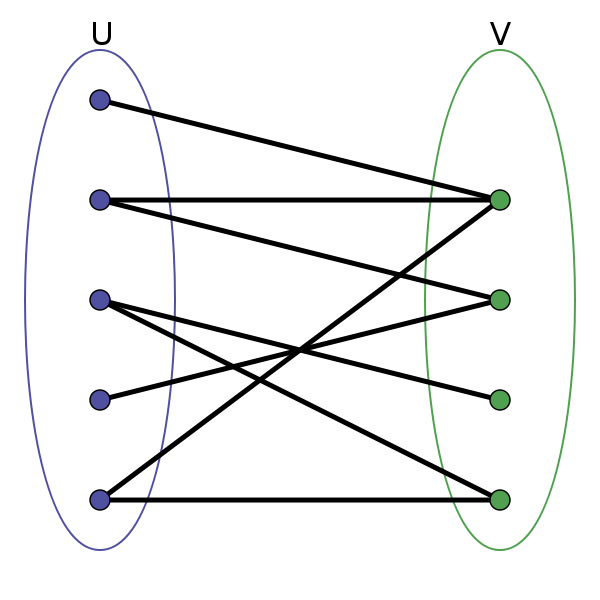
二分圖的頂點集可分割為兩個互不相交的子集，圖中每條邊依附的兩個頂點都分屬於這兩個子集，且兩個子集內的頂點不相鄰。

給你一幅「圖」，請你用兩種顏色將圖中的所有頂點着色，且使得任意一條邊的兩個端點的顏色都不相同，你能做到嗎？

這就是圖的「雙色問題」，其實這個問題就等同於二分圖的判定問題，如果你能夠成功地將圖染色，那麼這幅圖就是一幅二分圖，反之則不是

DFS

// 記錄圖是否符合二分圖性質
private boolean ok = true;
// 記錄圖中節點的顏色，false 和 true 代表兩種不同顏色
private boolean[] color;
// 記錄圖中節點是否被訪問過
private boolean[] visited;

// 主函數，輸入鄰接表，判斷是否是二分圖
public boolean isBipartite(int[][] graph) {
    int n = graph.length;
    color =  new boolean[n];
    visited =  new boolean[n];
    // 因為圖不一定是聯通的，可能存在多個子圖
    // 所以要把每個節點都作為起點進行一次遍歷
    // 如果發現任何一個子圖不是二分圖，整幅圖都不算二分圖
    for (int v = 0; v < n; v++) {
        if (!visited[v]) {
            traverse(graph, v);
        }
    }
    return ok;
}

// DFS 遍歷框架
private void traverse(int[][] graph, int v) {
    // 如果已經確定不是二分圖了，就不用浪費時間再遞歸遍歷了
    if (!ok) return;

    visited[v] = true;
    for (int w : graph[v]) {
        if (!visited[w]) {
            // 相鄰節點 w 沒有被訪問過
            // 那麼應該給節點 w 塗上和節點 v 不同的顏色
            color[w] = !color[v];
            // 繼續遍歷 w
            traverse(graph, w);
        } else {
            // 相鄰節點 w 已經被訪問過
            // 根據 v 和 w 的顏色判斷是否是二分圖
            if (color[w] == color[v]) {
                // 若相同，則此圖不是二分圖
                ok = false;
            }
        }
    }
}

BFS

// 記錄圖是否符合二分圖性質
private boolean ok = true;
// 記錄圖中節點的顏色，false 和 true 代表兩種不同顏色
private boolean[] color;
// 記錄圖中節點是否被訪問過
private boolean[] visited;

public boolean isBipartite(int[][] graph) {
    int n = graph.length;
    color =  new boolean[n];
    visited =  new boolean[n];
    
    for (int v = 0; v < n; v++) {
        if (!visited[v]) {
            // 改為使用 BFS 函數
            bfs(graph, v);
        }
    }
    
    return ok;
}

// 從 start 節點開始進行 BFS 遍歷
private void bfs(int[][] graph, int start) {
    Queue<Integer> q = new LinkedList<>();
    visited[start] = true;
    q.offer(start);
    
    while (!q.isEmpty() && ok) {
        int v = q.poll();
        // 從節點 v 向所有相鄰節點擴散
        for (int w : graph[v]) {
            if (!visited[w]) {
                // 相鄰節點 w 沒有被訪問過
                // 那麼應該給節點 w 塗上和節點 v 不同的顏色
                color[w] = !color[v];
                // 標記 w 節點，並放入隊列
                visited[w] = true;
                q.offer(w);
            } else {
                // 相鄰節點 w 已經被訪問過
                // 根據 v 和 w 的顏色判斷是否是二分圖
                if (color[w] == color[v]) {
                    // 若相同，則此圖不是二分圖
                    ok = false;
                }
            }
        }
    }
}

Union-Find並查集

大白話就是當我們需要判斷兩個元素是否在同一個集合裏的時候，我們就要想到用並查集。

並查集主要有兩個功能：

• 將兩個元素添加到一個集合中。
• 判斷兩個元素在不在同一個集合

名稱"並查集"直接體現了它的核心功能：合併集合與查詢元素所屬集合。在英文中，它通常被稱為"Union-Find"數據結構或"Disjoint-Set"數據結構。

並查集的基本思想是使用樹形結構來表示每個集合，樹的根節點作為集合的代表元素。

並查集核心特性：

1. 快速查找：能夠快速判斷兩個元素是否屬於同一集合
2. 快速合併：能夠快速將兩個集合合併為一個
3. 路徑壓縮：優化查找操作，使樹的高度儘量小
4. 按秩合併：優化合並操作，減少樹的高度增長

Union-Find 算法主要需要實現這兩個 API：

class UF {
    /* 將 p 和 q 連接 */
    public void union(int p, int q);
    /* 判斷 p 和 q 是否連通 */
    public boolean connected(int p, int q);
    /* 返回圖中有多少個連通分量 */
    public int count();
}

這裏所説的「連通」是一種等價關係，也就是説具有如下三個性質：

1、自反性：節點p和p是連通的。

2、對稱性：如果節點p和q連通，那麼q和p也連通。

3、傳遞性：如果節點p和q連通，q和r連通，那麼p和r也連通。

比如説有一幅圖，0～9 任意兩個不同的點都不連通，調用connected都會返回 false，連通分量為 10 個。

如果現在調用union(0, 1)，那麼 0 和 1 被連通，連通分量降為 9 個。

再調用union(1, 2)，這時 0,1,2 都被連通，調用connected(0, 2)也會返回 true，連通分量變為 8 個。

基礎算法

設定樹的每個節點有一個指針指向其父節點，如果是根節點的話，這個指針指向自己。比如説剛才那幅 10 個節點的圖，一開始的時候沒有相互連通，就是這樣：

class UF {
    // 記錄連通分量
    private int count;
    // 節點 x 的節點是 parent[x]
    private int[] parent;

    /* 構造函數，n 為圖的節點總數 */
    public UF(int n) {
        // 一開始互不連通
        this.count = n;
        // 父節點指針初始指向自己
        parent = new int[n];
        for (int i = 0; i < n; i++)
            parent[i] = i;
    }

    /* 其他函數 */
}

如果某兩個節點被連通，則讓其中的（任意）一個節點的根節點接到另一個節點的根節點上：

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 將兩棵樹合併為一棵
    parent[rootP] = rootQ;
    // parent[rootQ] = rootP 也一樣
    count--; // 兩個分量合二為一
}

/* 返回某個節點 x 的根節點 */
private int find(int x) {
    // 根節點的 parent[x] == x
    while (parent[x] != x)
        x = parent[x];
    return x;
}

/* 返回當前的連通分量個數 */
public int count() { 
    return count;
}

這樣，如果節點p和q連通的話，它們一定擁有相同的根節點：

public boolean connected(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    return rootP == rootQ;
}

至此，Union-Find 算法就基本完成了。

那麼這個算法的複雜度是多少呢？我們發現，主要 APIconnected和union中的複雜度都是find函數造成的，所以説它們的複雜度和find一樣。

find主要功能就是從某個節點向上遍歷到樹根，其時間複雜度就是樹的高度。我們可能習慣性地認為樹的高度就是logN，但這並不一定。logN的高度只存在於平衡二叉樹，對於一般的樹可能出現極端不平衡的情況，使得「樹」幾乎退化成「鏈表」，樹的高度最壞情況下可能變成N。

所以説上面這種解法，find,union,connected的時間複雜度都是 O(N)。這個複雜度很不理想的，你想圖論解決的都是諸如社交網絡這樣數據規模巨大的問題，對於union和connected的調用非常頻繁，每次調用需要線性時間完全不可忍受。

平衡性優化

要知道哪種情況下可能出現不平衡現象，關鍵在於union過程：

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 將兩棵樹合併為一棵
    parent[rootP] = rootQ;
    // parent[rootQ] = rootP 也可以
    count--; 
}

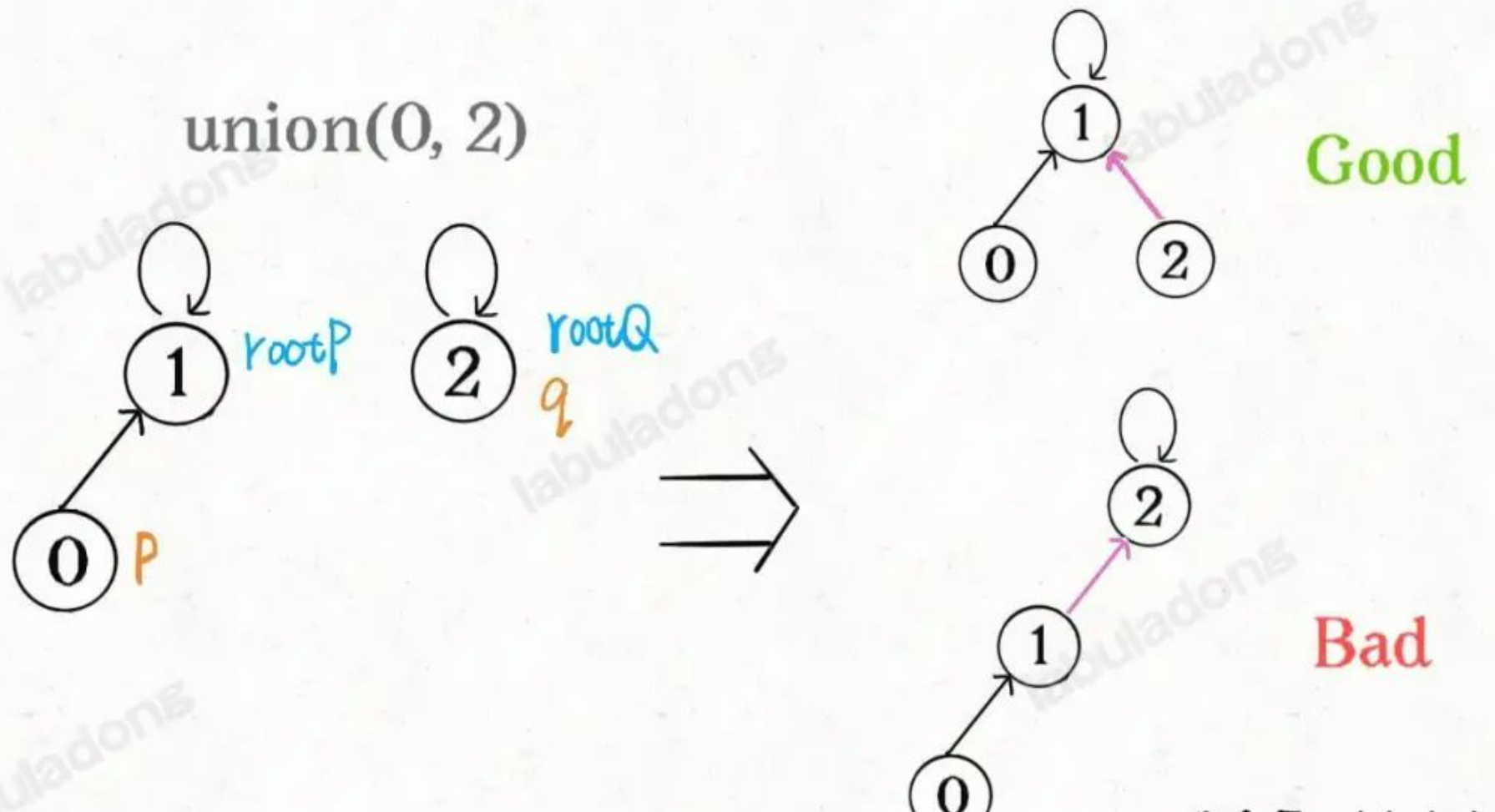
我們一開始就是簡單粗暴的把p所在的樹接到q所在的樹的根節點下面，那麼這裏就可能出現「頭重腳輕」的不平衡狀況，比如下面這種局面：

長此以往，樹可能生長得很不平衡。我們其實是希望，小一些的樹接到大一些的樹下面，這樣就能避免頭重腳輕，更平衡一些。解決方法是額外使用一個size數組，記錄每棵樹包含的節點數，我們不妨稱為「重量」：

class UF {
    private int count;
    private int[] parent;
    // 新增一個數組記錄樹的“重量”
    private int[] size;

    public UF(int n) {
        this.count = n;
        parent = new int[n];
        // 最初每棵樹只有一個節點
        // 重量應該初始化 1
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    /* 其他函數 */
}

比如説size[3] = 5表示，以節點3為根的那棵樹，總共有5個節點。這樣我們可以修改一下union方法：

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;

    // 小樹接到大樹下面，較平衡
    if (size[rootP] > size[rootQ]) {
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ];
    } else {
        parent[rootP] = rootQ;
        size[rootQ] += size[rootP];
    }
    count--;
}

這樣，通過比較樹的重量，就可以保證樹的生長相對平衡，樹的高度大致在logN這個數量級，極大提升執行效率。

此時，find,union,connected的時間複雜度都下降為 O(logN)，即便數據規模上億，所需時間也非常少。

路徑壓縮

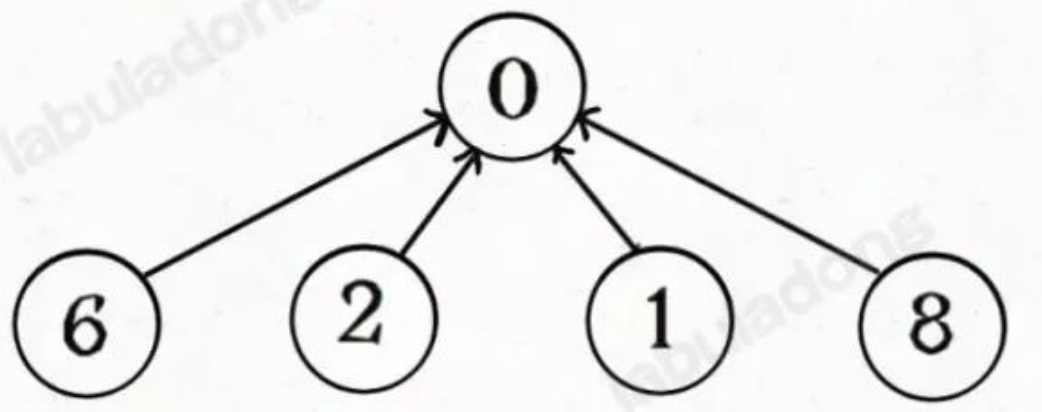
其實我們並不在乎每棵樹的結構長什麼樣，只在乎根節點。

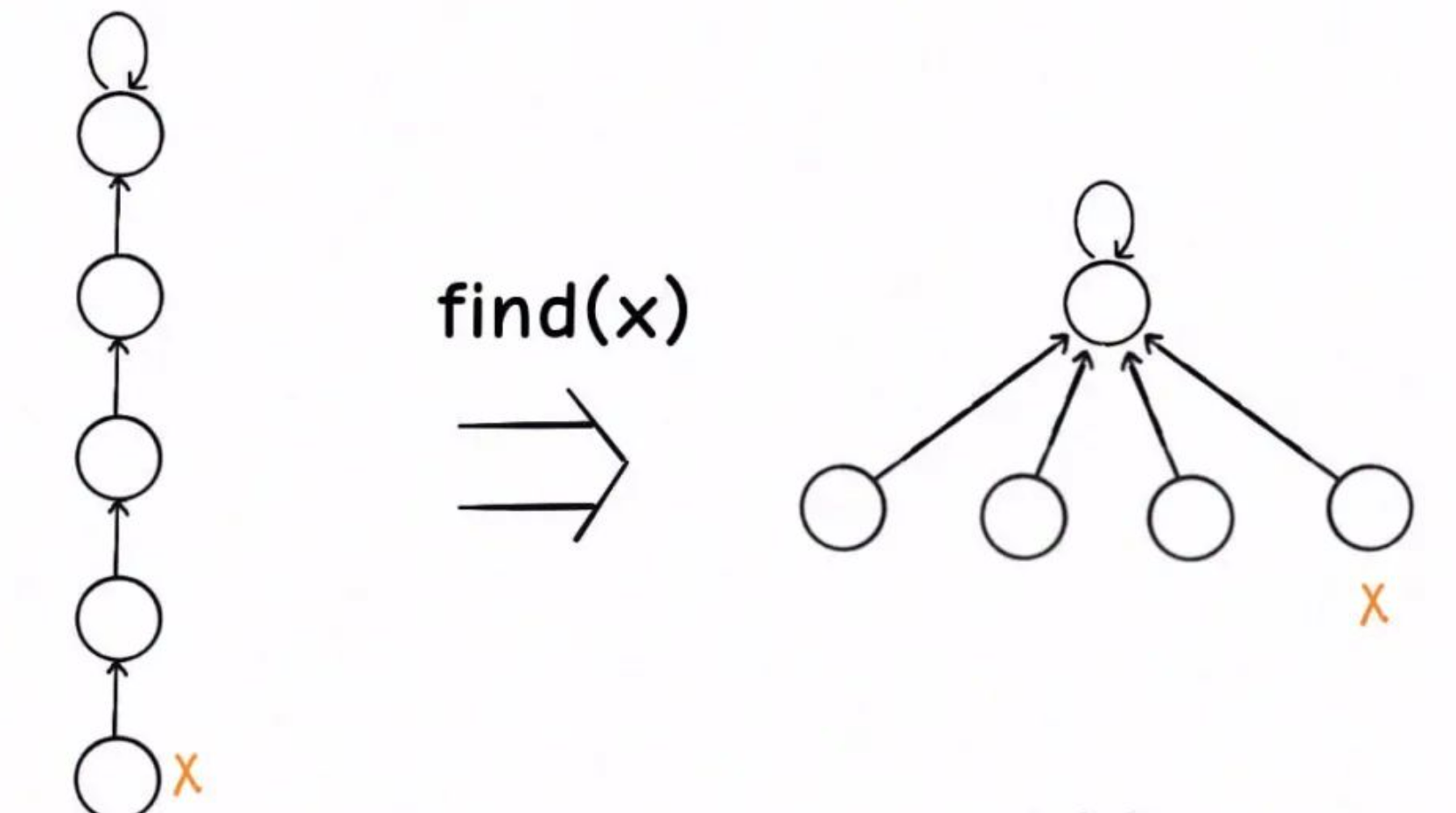
因為無論樹長啥樣，樹上的每個節點的根節點都是相同的，所以能不能進一步壓縮每棵樹的高度，使樹高始終保持為常數？

如圖所示，這樣每個節點的父節點就是整棵樹的根節點，find就能以 O(1) 的時間找到某一節點的根節點，相應的，connected和union複雜度都下降為 O(1)。

要做到這一點主要是修改find函數邏輯，非常簡單，但你可能會看到兩種不同的寫法。

第一種是在find中加一行代碼：

private int find(int x) {
    while (parent[x] != x) {
        // 這行代碼進行路徑壓縮
        parent[x] = parent[parent[x]];
        x = parent[x];
    }
    return x;
}

用語言描述就是，每次 while 循環都會把一對兒父子節點改到同一層，這樣每次調用find函數向樹根遍歷的同時，順手就將樹高縮短了。

路徑壓縮的第二種寫法是這樣：

// 第二種路徑壓縮的 find 方法
public int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

這個遞歸過程有點不好理解，你可以自己手畫一下遞歸過程。我把這個函數做的事情翻譯成迭代形式，方便你理解它進行路徑壓縮的原理：

// 這段迭代代碼方便你理解遞歸代碼所做的事情
public int find(int x) {
    // 先找到根節點
    int root = x;
    while (parent[root] != root) {
        root = parent[root];
    }
    // 然後把 x 到根節點之間的所有節點直接接到根節點下面
    int old_parent = parent[x];
    while (x != root) {
        parent[x] = root;
        x = old_parent;
        old_parent = parent[old_parent];
    }
    return root;
}

這種路徑壓縮的效果如下：

比起第一種路徑壓縮，顯然這種方法壓縮得更徹底，直接把一整條樹枝壓平，一點意外都沒有。就算一些極端情況下產生了一棵比較高的樹，只要一次路徑壓縮就能大幅降低樹高，從 攤還分析 的角度來看，所有操作的平均時間複雜度依然是 O(1)，所以從效率的角度來説，推薦你使用這種路徑壓縮算法。

另外，如果使用路徑壓縮技巧，那麼size數組的平衡優化就不是特別必要了。所以你一般看到的 Union Find 算法應該是如下實現：

class UF {
    // 連通分量個數
    private int count;
    // 存儲每個節點的父節點
    private int[] parent;

    // n 為圖中節點的個數
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    // 將節點 p 和節點 q 連通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);

        if (rootP == rootQ)
            return;

        parent[rootQ] = rootP;
        // 兩個連通分量合併成一個連通分量
        count--;
    }

    // 判斷節點 p 和節點 q 是否連通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 返回圖中的連通分量個數
    public int count() {
        return count;
    }
}

Union-Find 算法的複雜度可以這樣分析：構造函數初始化數據結構需要 O(N) 的時間和空間複雜度；連通兩個節點union、判斷兩個節點的連通性connected、計算連通分量count所需的時間複雜度均為 O(1)。

到這裏，相信你已經掌握了 Union-Find 算法的核心邏輯，總結一下我們優化算法的過程：

1、用parent數組記錄每個節點的父節點，相當於指向父節點的指針，所以parent數組內實際存儲着一個森林（若干棵多叉樹）。

2、用size數組記錄着每棵樹的重量，目的是讓union後樹依然擁有平衡性，保證各個 API 時間複雜度為 O(logN)，而不會退化成鏈表影響操作效率。

3、在find函數中進行路徑壓縮，保證任意樹的高度保持在常數，使得各個 API 時間複雜度為 O(1)。使用了路徑壓縮之後，可以不使用size數組的平衡優化。

優點

1. 查找和合並操作的平均時間複雜度接近O(1)
2. 實現簡單，易於理解
3. 空間複雜度低，只需要兩個數組
4. 適用於處理大量動態連通性問題

缺點

1. 不支持分裂操作（將一個集合分成兩個）
2. 不方便查詢集合中的所有元素
3. 在某些特殊情況下，性能可能退化

應用場景

Kruskal最小生成樹算法：在Kruskal算法中，並查集是核心數據結構。該算法按權重從小到大遍歷邊，使用並查集判斷加入某條邊是否會形成環，從而高效構建最小生成樹。

網絡連通性問題：並查集可高效解決動態連通性問題，比如判斷網絡中兩個節點是否連通、社交網絡中用户間的關係連接等。當關系變化時，只需執行簡單的union操作，判斷連通性時使用find操作即可。

等價類劃分：在編譯器設計、電路分析等領域，並查集可用於等價類識別與合併。當系統發現兩個元素等價時執行union操作，需要判斷等價關係時使用find操作，這種動態維護等價關係的能力正是並查集的優勢所在。

判斷無向圖中的環：當向無向圖中添加邊時，如果邊的兩個端點已在同一個集合中，則添加這條邊會形成環。在很多圖算法和網絡設計問題中都可以使用這一特性。

Kruskal 最小生成樹算法

Kruskal 的 關鍵就是 並查集算法

先説「樹」和「圖」的根本區別：樹不會包含環，圖可以包含環。

如果一幅圖沒有環，完全可以拉伸成一棵樹的模樣。説的專業一點，樹就是「無環連通圖」。

那麼什麼是圖的「生成樹」呢，其實按字面意思也好理解，就是在圖中找一棵包含圖中的所有節點的樹。專業點説，生成樹是含有圖中所有頂點的「無環連通子圖」。

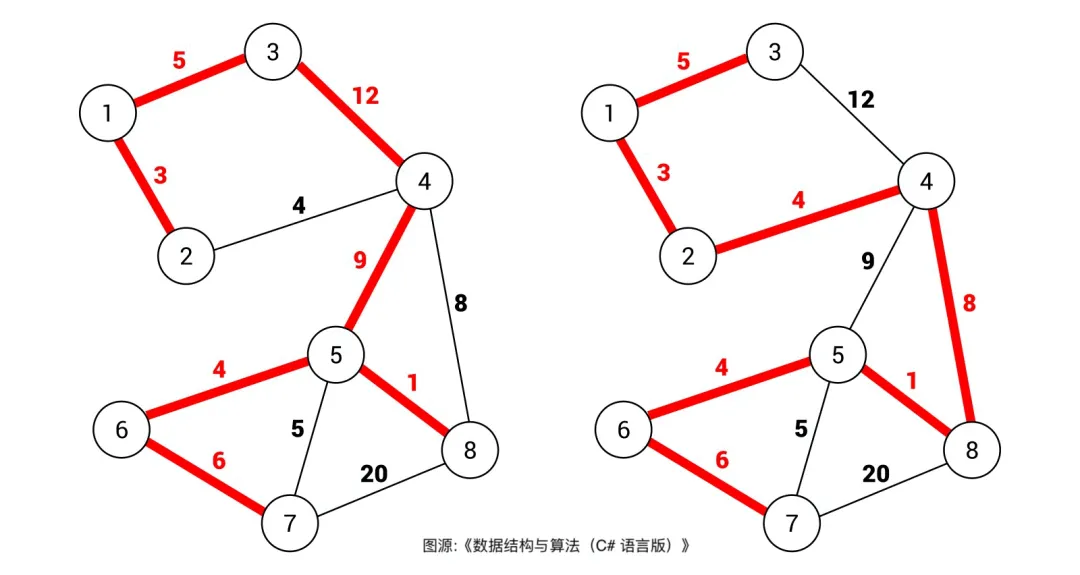
容易想到，一幅圖可以有很多不同的生成樹，比如下面這幅圖，紅色的邊就組成了兩棵不同的生成樹：

對於加權圖，每條邊都有權重，所以每棵生成樹都有一個權重和。比如上圖，右側生成樹的權重和顯然比左側生成樹的權重和要小。

那麼最小生成樹很好理解了，所有可能的生成樹中，權重和最小的那棵生成樹就叫「最小生成樹」。

PS：一般來説，我們都是在無向加權圖中計算最小生成樹的，所以使用最小生成樹算法的現實場景中，圖的邊權重一般代表成本、距離這樣的標量。

所謂最小生成樹，就是圖中若干邊的集合（我們後文稱這個集合為mst，最小生成樹的英文縮寫），你要保證這些邊：

1、包含圖中的所有節點。

2、形成的結構是樹結構（即不存在環）。

3、權重和最小。

前兩條其實可以很容易地利用 Union-Find 算法做到，關鍵在於第 3 點，如何保證得到的這棵生成樹是權重和最小的。

這裏就用到了貪心思路：將所有邊按照權重從小到大排序，從權重最小的邊開始遍歷，如果這條邊和mst中的其它邊不會形成環，則這條邊是最小生成樹的一部分，將它加入mst集合；否則，這條邊不是最小生成樹的一部分，不要把它加入mst集合。

這樣，最後mst集合中的邊就形成了最小生成樹，算法代碼如下：

int minimumCost(int n, int[][] connections) {
    // 城市編號為 1...n，所以初始化大小為 n + 1
    UF uf = new UF(n + 1);
    // 對所有邊按照權重從小到大排序
    Arrays.sort(connections, (a, b) -> (a[2] - b[2]));
    // 記錄最小生成樹的權重之和
    int mst = 0;
    for (int[] edge : connections) {
        int u = edge[0];
        int v = edge[1];
        int weight = edge[2];
        // 若這條邊會產生環，則不能加入 mst
        if (uf.connected(u, v)) {
            continue;
        }
        // 若這條邊不會產生環，則屬於最小生成樹
        mst += weight;
        uf.union(u, v);
    }
    // 保證所有節點都被連通
    // 按理説 uf.count() == 1 説明所有節點被連通
    // 但因為節點 0 沒有被使用，所以 0 會額外佔用一個連通分量
    return uf.count() == 2 ? mst : -1;
}

class UF {
    // 見上文並查集代碼實現
}

複雜度分析：

假設一幅圖的節點個數為V，邊的條數為E，首先需要O(E)的空間裝所有邊，而且 Union-Find 算法也需要O(V)的空間，所以 Kruskal 算法總的空間複雜度就是O(V + E)。

時間複雜度主要耗費在排序，需要O(ElogE)的時間，Union-Find 算法所有操作的複雜度都是O(1)，套一個 for 循環也不過是O(E)，所以總的時間複雜度為O(ElogE)。

PRIM 最小生成樹算法

Prim 算法也使用貪心思想來讓生成樹的權重儘可能小，也就是「切分定理」。

其次，Prim 算法使用 BFS 算法思想 和 visited 布爾數組避免成環，來保證選出來的邊最終形成的一定是一棵樹。

Prim 算法不需要事先對所有邊排序，而是利用優先級隊列動態實現排序的效果，所以 Prim 算法類似於 Kruskal 的動態過程。

切分定理：對於任意一種「切分」，其中權重最小的那條「橫切邊」一定是構成最小生成樹的一條邊。只要把圖中的節點切成兩個不重疊且非空的節點集合即可算作一個合法的「切分」

反證法證明：給定一幅圖的最小生成樹，那麼隨便給一種「切分」，一定至少有一條「橫切邊」屬於最小生成樹。假設這條「橫切邊」不是權重最小的，那説明最小生成樹的權重和就還有再減小的餘地，那這就矛盾了，最小生成樹的權重和本來就是最小的，怎麼再減？所以切分定理是正確的。

算法實現：Prim 算法的邏輯就是，每次切分都能找到最小生成樹的一條邊，然後又可以進行新一輪切分，直到找到最小生成樹的所有邊為止。

class Prim {
    // 核心數據結構，存儲「橫切邊」的優先級隊列
    private PriorityQueue<int[]> pq;
    // 類似 visited 數組的作用，記錄哪些節點已經成為最小生成樹的一部分
    private boolean[] inMST;
    // 記錄最小生成樹的權重和
    private int weightSum = 0;
    // graph 是用鄰接表表示的一幅圖，
    // graph[s] 記錄節點 s 所有相鄰的邊，
    // 三元組 int[]{from, to, weight} 表示一條邊
    private List<int[]>[] graph;

    public Prim(List<int[]>[] graph) {
        this.graph = graph;
        this.pq = new PriorityQueue<>((a, b) -> {
            // 按照邊的權重從小到大排序
            return a[2] - b[2];
        });
        // 圖中有 n 個節點
        int n = graph.length;
        this.inMST = new boolean[n];

        // 隨便從一個點開始切分都可以，我們不妨從節點 0 開始
        inMST[0] = true;
        cut(0);
        // 不斷進行切分，向最小生成樹中添加邊
        while (!pq.isEmpty()) {
            int[] edge = pq.poll();
            int to = edge[1];
            int weight = edge[2];
            if (inMST[to]) {
                // 節點 to 已經在最小生成樹中，跳過
                // 否則這條邊會產生環
                continue;
            }
            // 將邊 edge 加入最小生成樹
            weightSum += weight;
            inMST[to] = true;
            // 節點 to 加入後，進行新一輪切分，會產生更多橫切邊
            cut(to);
        }
    }

    // 將 s 的橫切邊加入優先隊列
    private void cut(int s) {
        // 遍歷 s 的鄰邊
        for (int[] edge : graph[s]) {
            int to = edge[1];
            if (inMST[to]) {
                // 相鄰接點 to 已經在最小生成樹中，跳過
                // 否則這條邊會產生環
                continue;
            }
            // 加入橫切邊隊列
            pq.offer(edge);
        }
    }

    // 最小生成樹的權重和
    public int weightSum() {
        return weightSum;
    }

    // 判斷最小生成樹是否包含圖中的所有節點
    public boolean allConnected() {
        for (int i = 0; i < inMST.length; i++) {
            if (!inMST[i]) {
                return false;
            }
        }
        return true;
    }
}

複雜度分析：

複雜度主要在優先級隊列 pq 的操作上，由於 pq 裏面裝的是圖中的「邊」，假設一幅圖邊的條數為 E，那麼最多操作 O(E) 次 pq。每次操作優先級隊列的時間複雜度取決於隊列中的元素個數，取最壞情況就是 O(logE)。

這種 Prim 算法實現的總時間複雜度是 O(ElogE)

Dijkstra 最短路徑規劃算法

算法簽名：

// 輸入一幅圖和一個起點 start，計算 start 到其他節點的最短距離
int[] dijkstra(int start, List<Integer>[] graph);

輸入是一幅圖 graph 和一個起點 start，返回是一個記錄最短路徑權重的數組。

比方説，輸入起點 start = 3，函數返回一個 int[] 數組，假設賦值給 distTo 變量，那麼從起點 3 到節點 6 的最短路徑權重的值就是 distTo[6]。標準的 Dijkstra 算法會把從起點 start 到所有其他節點的最短路徑都算出來。

class State {
    // 圖節點的 id
    int id;
    // 從 start 節點到當前節點的距離
    int distFromStart;

    State(int id, int distFromStart) {
        this.id = id;
        this.distFromStart = distFromStart;
    }
}

使用 distFromStart 變量記錄從起點 start 到當前這個節點的距離。

普通 BFS 算法中，根據 BFS 的邏輯和無權圖的特點，第一次遇到某個節點所走的步數就是最短距離，所以用一個 visited 數組防止走回頭路，每個節點只會經過一次。

加權圖中的 Dijkstra 算法和無權圖中的普通 BFS 算法不同，在 Dijkstra 算法中，你第一次經過某個節點時的路徑權重，不見得就是最小的，所以對於同一個節點，可能會經過多次，而且每次的 distFromStart 可能都不一樣，取 distFromStart 最小的那次，就是從起點 start 到節點 5 的最短路徑權重

Dijkstra 可以理解成一個帶 dp table（或者説備忘錄）的 BFS 算法，偽碼如下：

// 返回節點 from 到節點 to 之間的邊的權重
int weight(int from, int to);

// 輸入節點 s 返回 s 的相鄰節點
List<Integer> adj(int s);

// 輸入一幅圖和一個起點 start，計算 start 到其他節點的最短距離
int[] dijkstra(int start, List<Integer>[] graph) {
    // 圖中節點的個數
    int V = graph.length;
    // 記錄最短路徑的權重，你可以理解為 dp table
    // 定義：distTo[i] 的值就是節點 start 到達節點 i 的最短路徑權重
    int[] distTo = new int[V];
    // 求最小值，所以 dp table 初始化為正無窮
    Arrays.fill(distTo, Integer.MAX_VALUE);
    // base case，start 到 start 的最短距離就是 0
    distTo[start] = 0;

    // 優先級隊列，distFromStart 較小的排在前面
    Queue<State> pq = new PriorityQueue<>((a, b) -> {
        return a.distFromStart - b.distFromStart;
    });

    // 從起點 start 開始進行 BFS
    pq.offer(new State(start, 0));

     while (!pq.isEmpty()) {
        State curState = pq.poll();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;

        if (curDistFromStart > distTo[curNodeID]) {
            // 已經有一條更短的路徑到達 curNode 節點了
            continue;
        }
        // 將 curNode 的相鄰節點裝入隊列
        for (int nextNodeID : adj(curNodeID)) {
            // 看看從 curNode 達到 nextNode 的距離是否會更短
            int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
            if (distTo[nextNodeID] > distToNextNode) {
                // 更新 dp table
                distTo[nextNodeID] = distToNextNode;
                // 將這個節點以及距離放入隊列
                pq.offer(new State(nextNodeID, distToNextNode));
            }
        }
    }
    return distTo;
}

計算起點到終點end的最短距離

// 輸入起點 start 和終點 end，計算起點到終點的最短距離
int dijkstra(int start, int end, List<Integer>[] graph) {

    // ...

    while (!pq.isEmpty()) {
        State curState = pq.poll();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;

        // 在這裏加一個判斷就行了，其他代碼不用改
        if (curNodeID == end) {
            return curDistFromStart;
        }

        if (curDistFromStart > distTo[curNodeID]) {
            continue;
        }

        // ...
    }

    // 如果運行到這裏，説明從 start 無法走到 end
    return Integer.MAX_VALUE;
}

A* 算法

Dijkstra算法的優點在於其簡單可靠，能夠保證找到全局最優解。然而，其缺點也明顯：對大規模圖的處理效率低下，因為它需要遍歷整個圖。

Astar 是一種 廣搜的改良版。有的 Astar是 dijkstra 的改良版。

其實只是場景不同而已，在搜索最短路的時候， 如果是無權圖（邊的權值都是1） 那就用廣搜，代碼簡潔，時間效率和 dijkstra 差不多 （具體要取決於圖的稠密）如果是有權圖（邊有不同的權值），優先考慮 dijkstra。

而 Astar 關鍵在於 啓發式函數， 也就是 影響 廣搜或者 dijkstra 從 容器（隊列）裏取元素的優先順序。

實現機制

1. 啓發式搜索的優勢
   A*算法引入了啓發式函數h(v)，它預估了從節點v到目標節點的最優路徑成本。這使得A*能夠在搜索過程中具有方向性，優先探索那些更有可能導向目標的路徑，從而減少不必要的探索，提高搜索效率。

2. 實現機制

   • 評估函數：A*的關鍵在於f(v)=g(v)+h(v)，其中g(v)是從起點到節點v的實際成本，h(v)是啓發式函數，通常表示 當前節點 到終點的距離。因此兩者相加就是起點到終點的距離。

   • 開放與關閉集合：算法維護兩個集合，開放集合存放待評估的節點，關閉集合存放已評估節點。每次迭代從開放集合中選擇f值最小的節點進行擴展，直到目標節點被加入關閉集合。

BFS 是沒有目的性的 一圈一圈去搜索， 而 A* 是有方向性的去搜索。

那麼 A* 為什麼可以有方向性的去搜索，它的如何知道方向呢？其關鍵在於 啓發式函數。

計算兩點距離通常有如下三種計算方式：這也一般被選為啓發式函數，用來預估當前節點到終點的距離

1. 曼哈頓距離，計算方式：d = abs(x1-x2)+abs(y1-y2)
2. 歐氏距離（歐拉距離） ，計算方式：d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
3. 切比雪夫距離，計算方式：d = max(abs(x1 - x2), abs(y1 - y2))

與Dijkstra的對比分析

• 計算效率：A*由於採用了啓發式信息，通常比Dijkstra算法更快找到解，尤其在複雜路網中更為顯著。
• 路徑質量：理論上，只要啓發式函數滿足可接納性條件，A*保證找到最短路徑。Dijkstra同樣保證最短路徑，但缺乏效率優勢。
• 資源消耗：A*在內存使用上可能更高，因為它需要維護開放集合和關閉集合，而Dijkstra只需維護未訪問集合和前驅節點映射。
• 適用場景：Dijkstra適用於小型或中型規模、對實時性要求不高的場景；A*更適合大型圖搜索或對實時性要求較高的無場景。

代碼實現

實現代碼如下：啓發式函數 採用 歐拉距離計算方式

class Node {
    //表示節點在網格中的位置
    int x, y;
    //gCost表示從起點到該節點的實際代價，hCost表示從該節點到目標節點的估計代價（啓發式值），fCost是兩者之和。
    double gCost, hCost, fCost;
    //用於重構路徑
    Node parent;

    public Node(int x, int y) {
        this.x = x;
        this.y = x;
    }

    //計算當前節點到目標節點的歐拉距離。
    public double calculateHeuristic(Node target) {
        return Math.sqrt(Math.pow(this.x - target.x, 2) + Math.pow(this.y - target.y, 2));
    }

    public void updateCosts(Node target, double gCost) {
        this.gCost = gCost;
        this.hCost = calculateHeuristic(target);
        this.fCost = this.gCost + this.hCost;
    }

    @Override
    public boolean equals(Object obj) {
        if (this == obj) return true;
        if (obj == null || getClass() != obj.getClass()) return false;
        Node node = (Node) obj;
        return x == node.x && y == node.y;
    }

    @Override
    public int hashCode() {
        return Objects.hash(x, y);
    }
}

class AStar {
    private static final int[][] DIRECTIONS = {{1, 0}, {-1, 0}, {0, 1}, {0, -1},
            {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};

    public List<Node> findPath(Node start, Node target, int[][] grid) {
        //表示待處理節點
        Set<Node> openSet = new HashSet<>();
        //表示已處理節點
        Set<Node> closedSet = new HashSet<>();
        //用於獲取具有最小fCost的節點
        PriorityQueue<Node> priorityQueue = new PriorityQueue<>(Comparator.comparingDouble(n -> n.fCost));

        start.updateCosts(target, 0);
        openSet.add(start);
        priorityQueue.add(start);

        while (!openSet.isEmpty()) {
            Node current = priorityQueue.poll();
            openSet.remove(current);
            closedSet.add(current);

            if (current.equals(target)) {
                return reconstructPath(current);
            }

            for (int[] direction : DIRECTIONS) {
                int newX = current.x + direction[0];
                int newY = current.y + direction[1];

                if (!isInBounds(newX, newY, grid) || grid[newX][newY] == 1) {
                    continue;
                }

                Node neighbor = new Node(newX, newY);
                if (closedSet.contains(neighbor)) {
                    continue;
                }

                double tentativeGCost = current.gCost + current.calculateHeuristic(neighbor);
                if (!openSet.contains(neighbor) || tentativeGCost < neighbor.gCost) {
                    neighbor.updateCosts(target, tentativeGCost);
                    neighbor.parent = current;

                    if (!openSet.contains(neighbor)) {
                        openSet.add(neighbor);
                        priorityQueue.add(neighbor);
                    }
                }
            }
        }
        return Collections.emptyList();
    }

    // 檢查節點是否在網格範圍內。
    private boolean isInBounds(int x, int y, int[][] grid) {
        return x >= 0 && y >= 0 && x < grid.length && y < grid[0].length;
    }

    //從目標節點回溯構建路徑。
    private List<Node> reconstructPath(Node node) {
        List<Node> path = new ArrayList<>();
        while (node != null) {
            path.add(node);
            node = node.parent;
        }
        Collections.reverse(path);
        return path;
    }
}

複雜度分析

A* 算法的時間複雜度 其實是不好去量化的，因為他取決於 啓發式函數怎麼寫。

• 最壞情況下，A* 退化成廣搜，算法的時間複雜度 是 O(n * 2)，n 為節點數量。

• 最佳情況，是從起點直接到終點，時間複雜度為 O(dlogd)，d 為起點到終點的深度。因為在搜索的過程中也需要堆排序，所以是 O(dlogd)。

實際上 A* 的時間複雜度是介於 最優 和最壞 情況之間， 可以 非常粗略的認為 A* 算法的時間複雜度是 O(nlogn) ，n 為節點數量。

A* 算法的空間複雜度 O(b ^ d) ,d 為起點到終點的深度，b 是 圖中節點間的連接數量

A* 的缺點

大家看上述 A * 代碼的時候，可以看到 我們向隊列裏添加了很多節點，但真正從隊列裏取出來的 僅僅是 靠啓發式函數判斷 距離終點最近的節點。

相對於普通BFS，A* 算法只從 隊列裏取出 距離終點最近的節點。

那麼問題來了，A* 在一次路徑搜索中，大量不需要訪問的節點都在隊列裏，會造成空間的過度消耗。

IDA* 算法對這一空間增長問題進行了優化，關於 IDA* 算法，後續再更新 //to do

另外還有一種場景 是 A* 解決不了的。

如果給出多個可能的目標，然後在這多個目標中選擇最近的目標，這種 A* 就不擅長了， A* 只擅長給出明確的目標 然後找到最短路徑。

如果是多個目標找最近目標（特別是潛在目標數量很多的時候），可以考慮 Dijkstra ，BFS 或者 Floyd。