查找算法詳情 - java sevencoding 博客

二分查找

二分查找（Binary Search）是一種高效的查找算法，也叫折半查找。核心思想：對於一個有序的數據集合，每次查找都將查找範圍縮小為原來的一半，直到找到目標值或確定目標值不存在。二分查找要求數據必須是有序的，經常應用於數組等支持隨機訪問的數據結構裏。跟線性查找相比，二分查找的效率要高得多，特別是對於大規模數據集。

算法步驟

確定查找範圍的左邊界 left 和右邊界 right
計算中間位置 mid = (left + right) / 2（注意整數溢出問題，更安全的做法是 mid = left + (right - left) / 2）
將中間位置的元素與目標值比較
- 如果中間元素等於目標值，查找成功，返回中間元素的位置
- 如果中間元素大於目標值，目標值可能在左半部分，將右邊界調整為 mid - 1
- 如果中間元素小於目標值，目標值可能在右半部分，將左邊界調整為 mid + 1
重複步驟2-3，直到找到目標值或者左邊界大於右邊界（此時表示目標值不存在）

核心特性：

要求有序：二分查找只適用於有序數據集合
時間複雜度：O(log n)，在大規模數據集上非常高效
空間複雜度：迭代實現為O(1)，遞歸實現為O(log n)（因為遞歸調用棧的深度）
隨機訪問：要求數據結構支持O(1)時間複雜度的隨機訪問（比如數組）

基礎實現

下面是二分查找算法在各種主流編程語言中的實現：

public class BinarySearch {
    // 迭代實現
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        
        while (left <= right) {
            // 避免整數溢出
            int mid = left + (right - left) / 2;
            
            // 找到目標值
            if (arr[mid] == target) {
                return mid;
            }
            // 在左半部分繼續查找
            else if (arr[mid] > target) {
                right = mid - 1;
            }
            // 在右半部分繼續查找
            else {
                left = mid + 1;
            }
        }
        
        // 未找到目標值
        return -1;
    }
    
    // 遞歸實現
    public static int binarySearchRecursive(int[] arr, int target, int left, int right) {
        if (left > right) {
            return -1;
        }
        
        int mid = left + (right - left) / 2;
        
        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] > target) {
            return binarySearchRecursive(arr, target, left, mid - 1);
        } else {
            return binarySearchRecursive(arr, target, mid + 1, right);
        }
    }
    
    // 測試
    public static void main(String[] args) {
        int[] arr = {2, 3, 4, 10, 40, 50, 70, 80};
        int target = 10;
        
        // 迭代方法
        int result = binarySearch(arr, target);
        if (result == -1) {
            System.out.println("元素 " + target + " 不存在於數組中");
        } else {
            System.out.println("元素 " + target + " 在數組中的索引為 " + result);
        }
        
        // 遞歸方法
        result = binarySearchRecursive(arr, target, 0, arr.length - 1);
        if (result == -1) {
            System.out.println("元素 " + target + " 不存在於數組中");
        } else {
            System.out.println("元素 " + target + " 在數組中的索引為 " + result);
        }
    }
}

優點

查找效率非常高，時間複雜度為 O(log n)
在大規模數據集上表現優異
實現相對簡單
不需要額外的空間（迭代實現）

缺點

要求數據必須是有序的
只適用於支持隨機訪問的數據結構（如數組）
對於頻繁插入和刪除的數據結構，維護有序性的成本很高
不適合小數據量的查找（這種情況下線性查找可能更快）

應用場景

二分查找在很多場景中都有廣泛的應用：

數據庫索引的實現（如 B 樹和 B+ 樹的查找過程）
查找最接近某個值的元素（下界查找和上界查找）
計算平方根等數值計算中（二分法求解）
猜數字遊戲（每次猜測中間值）
在旋轉排序數組中查找元素
查找數組中第一個或最後一個滿足某條件的元素

哈希查找

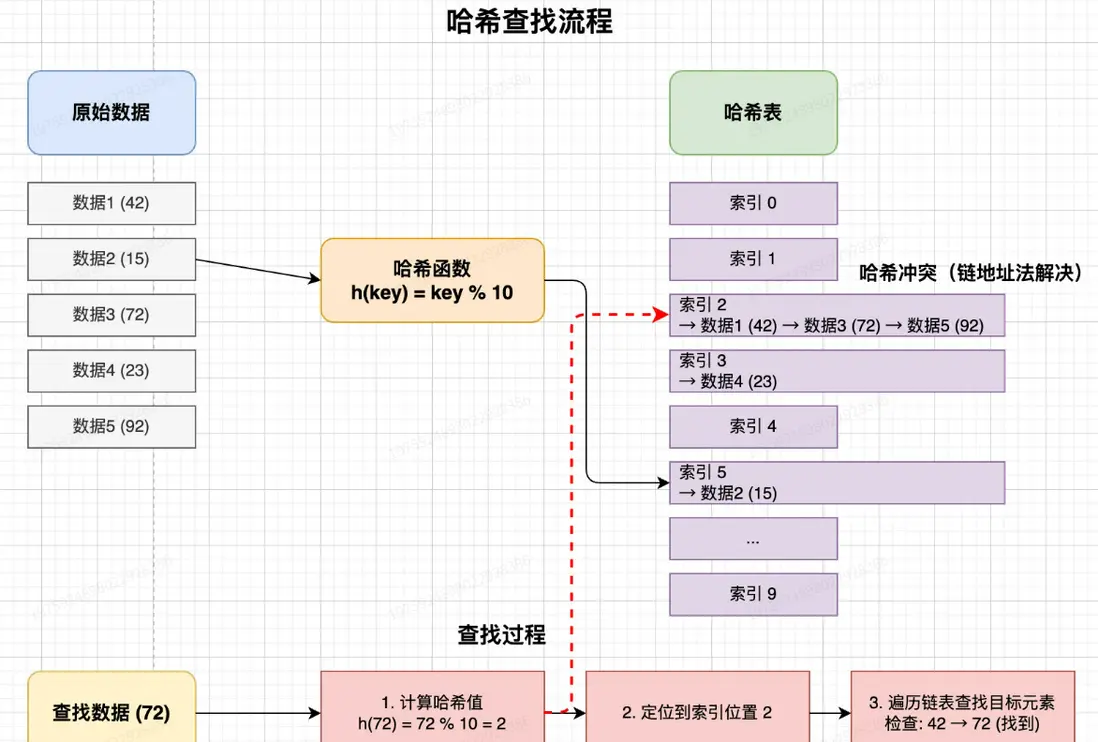
哈希查找（Hash Search），又稱散列查找，是一種高效的查找算法，它用哈希函數將數據轉換為數組下標，然後直接訪問數組中的元素。哈希查找的核心思想是將數據元素通過哈希函數映射到哈希表中的位置，實現快速查找。

在理想情況下，哈希查找的時間複雜度為 O(1)，這就意味着無論數據規模多大，查找操作都能在常數時間內完成，這是哈希查找相比其他查找算法（如二分查找、線性查找）的最大優勢。

不過使用哈希查找必須要考慮哈希衝突（不同的數據被映射到相同的位置）問題。

算法步驟

設計一個適合數據特點的哈希函數，將數據映射到哈希表的索引位置
構建哈希表，將所有元素通過哈希函數映射、存儲到相應位置
解決可能出現的哈希衝突（通常採用鏈地址法或開放尋址法）
查找時，通過同樣的哈希函數計算目標數據的哈希值
根據哈希值定位到哈希表中的位置
如果存在衝突，則按照解決衝突的方法查找目標元素

核心特性：

快速訪問：理想情況下查找時間複雜度為 O(1)
哈希函數：哈希查找的核心，將數據映射到數組索引的函數
哈希衝突：不同數據映射到相同位置的情況，需要特殊處理
空間換時間：通過額外的內存空間換取查找時間的提升
負載因子：表示哈希表的填充程度，影響查找效率和衝突概率
動態擴容：負載因子過高時，需要擴大哈希表並重新哈希所有元素

基礎實現

public class HashSearch {
    // 哈希表節點類
    static class Node {
        String key;
        int value;
        Node next;
        
        public Node(String key, int value) {
            this.key = key;
            this.value = value;
            this.next = null;
        }
    }
    
    // 哈希表類
    static class HashTable {
        private Node[] buckets;
        private int capacity;
        private int size;
        private final float LOAD_FACTOR = 0.75f; // 負載因子閾值
        
        public HashTable(int capacity) {
            this.capacity = capacity;
            this.buckets = new Node[capacity];
            this.size = 0;
        }
        
        // 哈希函數
        private int hash(String key) {
            int hash = 0;
            for (char c : key.toCharArray()) {
                hash = (hash * 31 + c) % capacity;
            }
            return Math.abs(hash);
        }
        
        // 插入鍵值對
        public void put(String key, int value) {
            if ((float)size / capacity >= LOAD_FACTOR) {
                resize(2 * capacity);
            }
            
            int index = hash(key);
            Node newNode = new Node(key, value);
            
            // 如果桶為空，直接插入
            if (buckets[index] == null) {
                buckets[index] = newNode;
                size++;
                return;
            }
            
            // 處理哈希衝突，使用鏈地址法
            Node current = buckets[index];
            
            // 檢查是否已存在相同的鍵
            while (current != null) {
                if (current.key.equals(key)) {
                    current.value = value; // 更新值
                    return;
                }
                if (current.next == null) {
                    break;
                }
                current = current.next;
            }
            
            // 在鏈表末尾添加新節點
            current.next = newNode;
            size++;
        }
        
        // 查找鍵對應的值
        public Integer get(String key) {
            int index = hash(key);
            Node current = buckets[index];
            
            // 遍歷鏈表查找匹配的鍵
            while (current != null) {
                if (current.key.equals(key)) {
                    return current.value;
                }
                current = current.next;
            }
            
            // 未找到
            return null;
        }
        
        // 刪除鍵值對
        public boolean remove(String key) {
            int index = hash(key);
            Node current = buckets[index];
            Node prev = null;
            
            // 查找目標節點
            while (current != null) {
                if (current.key.equals(key)) {
                    break;
                }
                prev = current;
                current = current.next;
            }
            
            // 未找到目標節點
            if (current == null) {
                return false;
            }
            
            // 刪除節點
            if (prev == null) {
                buckets[index] = current.next;
            } else {
                prev.next = current.next;
            }
            
            size--;
            return true;
        }
        
        // 擴容並重新哈希
        private void resize(int newCapacity) {
            Node[] oldBuckets = buckets;
            
            // 創建新的哈希表
            buckets = new Node[newCapacity];
            capacity = newCapacity;
            size = 0;
            
            // 重新哈希所有元素
            for (Node bucket : oldBuckets) {
                Node current = bucket;
                while (current != null) {
                    put(current.key, current.value);
                    current = current.next;
                }
            }
        }
    }
    
    public static void main(String[] args) {
        HashTable hashTable = new HashTable(10);
        
        // 插入數據
        hashTable.put("apple", 5);
        hashTable.put("banana", 10);
        hashTable.put("orange", 15);
        hashTable.put("grape", 20);
        
        // 查找數據
        System.out.println("apple: " + hashTable.get("apple"));
        System.out.println("banana: " + hashTable.get("banana"));
        System.out.println("orange: " + hashTable.get("orange"));
        System.out.println("grape: " + hashTable.get("grape"));
        System.out.println("watermelon: " + hashTable.get("watermelon"));
        
        // 刪除數據
        hashTable.remove("orange");
        System.out.println("After removing orange: " + hashTable.get("orange"));
    }
}

優點

查找、插入和刪除操作的平均時間複雜度為 O(1)
適用於快速查找
不要求數據有序，更靈活
支持動態數據集，高效地添加和刪除元素
通過合適的哈希函數和解決衝突策略，能實現非常優秀的性能

缺點

哈希衝突會降低查找效率，最壞情況下時間複雜度可能退化到 O(n)
需要額外的空間存儲哈希表
不支持範圍查詢，不適合按順序遍歷場景
負載因子過高會導致性能下降，過低會浪費空間

應用場景

哈希查找適用於以下場景：

需要快速查找、插入和刪除操作的數據結構，如字典或映射
實現緩存系統，比如LRU緩存、內存緩存等
數據庫索引，特別是等值查詢
符號表實現，如編譯器和解釋器中的變量表
去重操作，判斷元素是否已存在
網頁爬蟲的URL去重

一致性哈希

一致性哈希是分佈式系統中的重要概念，目的是儘可能少地重新分配數據

詳情可以看一致性哈希算法

布隆過濾器

布隆過濾器是一種空間效率高的概率型數據結構，判斷一個元素是否在集合中

詳情可以看布隆過濾器

sevencoding 博客

sevencoding 博客

博客 / 詳情

查找算法

二分查找

算法步驟

基礎實現

優點

缺點

應用場景

相關的 LeetCode 熱門題目

哈希查找

算法步驟

基礎實現

優點

缺點

應用場景

一致性哈希

布隆過濾器

相關的 LeetCode 熱門題目

發佈評論

Product

Company

Support

Company

博客 / 詳情

查找算法

二分查找

算法步驟

基礎實現

優點

缺點

應用場景

相關的 LeetCode 熱門題目

哈希查找

算法步驟

基礎實現

優點

缺點

應用場景

一致性哈希

布隆過濾器

相關的 LeetCode 熱門題目

發佈 評論

發佈評論