什麼是動態規劃
動態規劃,英文:Dynamic Programming,簡稱DP,如果某一問題有很多重疊子問題,使用動態規劃是最有效的。
所以動態規劃中每一個狀態一定是由上一個狀態推導出來的,這一點就區分於貪心,貪心沒有狀態推導,而是從局部直接選最優的,
例如:有N件物品和一個最多能背重量為W 的揹包。第i件物品的重量是weight[i],得到的價值是value[i] 。每件物品只能用一次,求解將哪些物品裝入揹包裏物品價值總和最大。
動態規劃中dp[j]是由dp[j-weight[i]]推導出來的,然後取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是貪心呢,每次拿物品選一個最大的或者最小的就完事了,和上一個狀態沒有關係。
所以貪心解決不了動態規劃的問題。
動態規劃的解題步驟
狀態轉移公式(遞推公式)是很重要,但動規不僅僅只有遞推公式。
對於動態規劃問題,可以拆解為如下五步曲:
- 確定dp數組(dp table)以及下標的含義
- 確定遞推公式
- dp數組如何初始化
- 確定遍歷順序
- 舉例推導dp數組
01揹包問題
題目描述:有n件物品和一個最多能背重量為w 的揹包。第i件物品的重量是weight[i],得到的價值是value[i] 。每件物品只能用一次,求解將哪些物品裝入揹包裏物品價值總和最大。
每一件物品其實只有兩個狀態,取或者不取,所以可以使用回溯法搜索出所有的情況,那麼時間複雜度就是$o(2^n)$,這裏的n表示物品數量。
所以暴力的解法是指數級別的時間複雜度。進而才需要動態規劃的解法來進行優化!
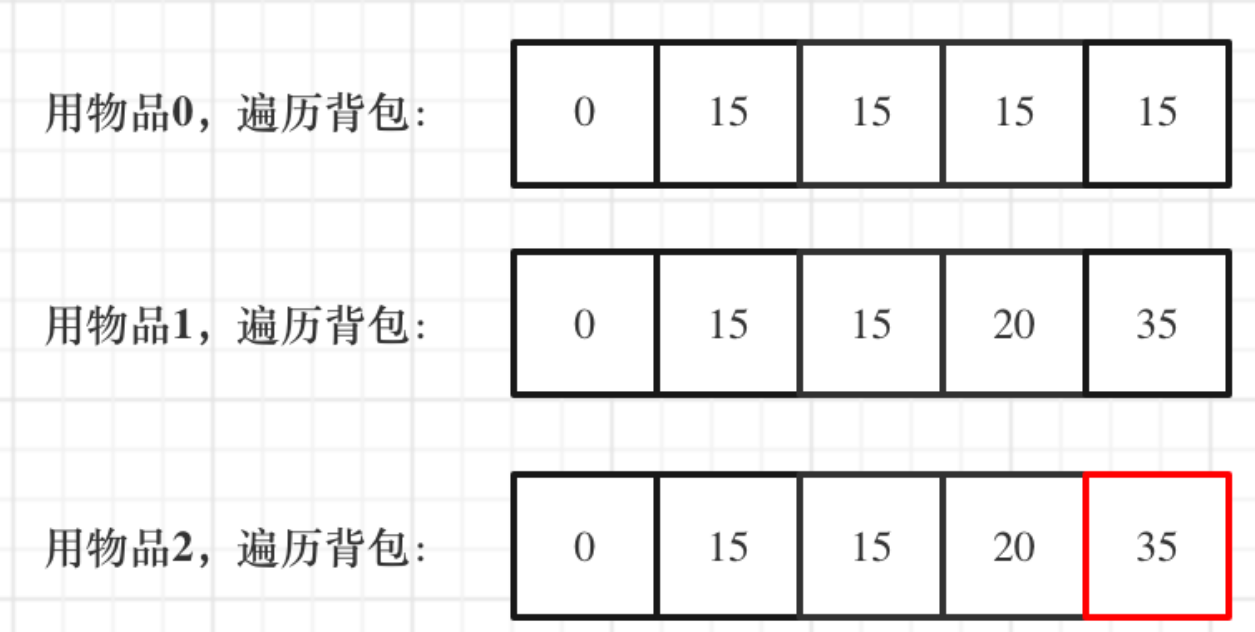
舉一個例子:揹包最大重量為4。
物品為:
| 重量 | 價值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
問揹包能背的物品最大價值是多少?
二維dp數組
- 確定dp數組以及下標的含義
對於揹包問題,有一種寫法, 是使用二維數組,即dp[i][j] 表示從下標為[0-i]的物品裏任意取,放進容量為j的揹包,價值總和最大是多少。
- 確定遞推公式
再回顧一下dp[i][j]]的含義:從下標為[0-i]的物品裏任意取,放進容量為j的揹包,價值總和最大是多少。
那麼可以有兩個方向推出來dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即揹包容量為j,裏面不放物品i的最大價值,此時dp[i][j]就是dp[i - 1][j]。(其實就是當物品i的重量大於揹包j的重量時,物品i無法放進揹包中,所以揹包內的價值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 為揹包容量為j - weight[i]的時候不放物品i的最大價值,那麼dp[i - 1][j - weight[i]] + value[i] (物品i的價值),就是揹包放物品i得到的最大價值
所以遞歸公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- dp數組如何初始化
關於初始化,一定要和dp數組的定義吻合,否則到遞推公式的時候就會越來越亂。
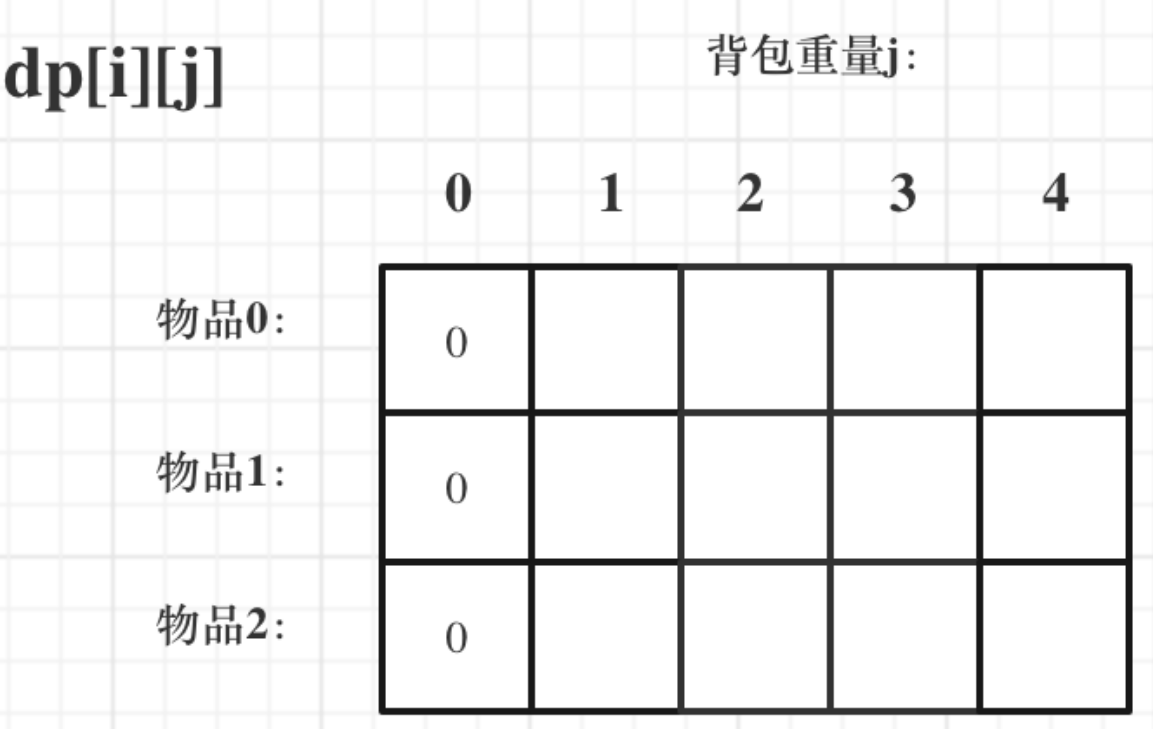
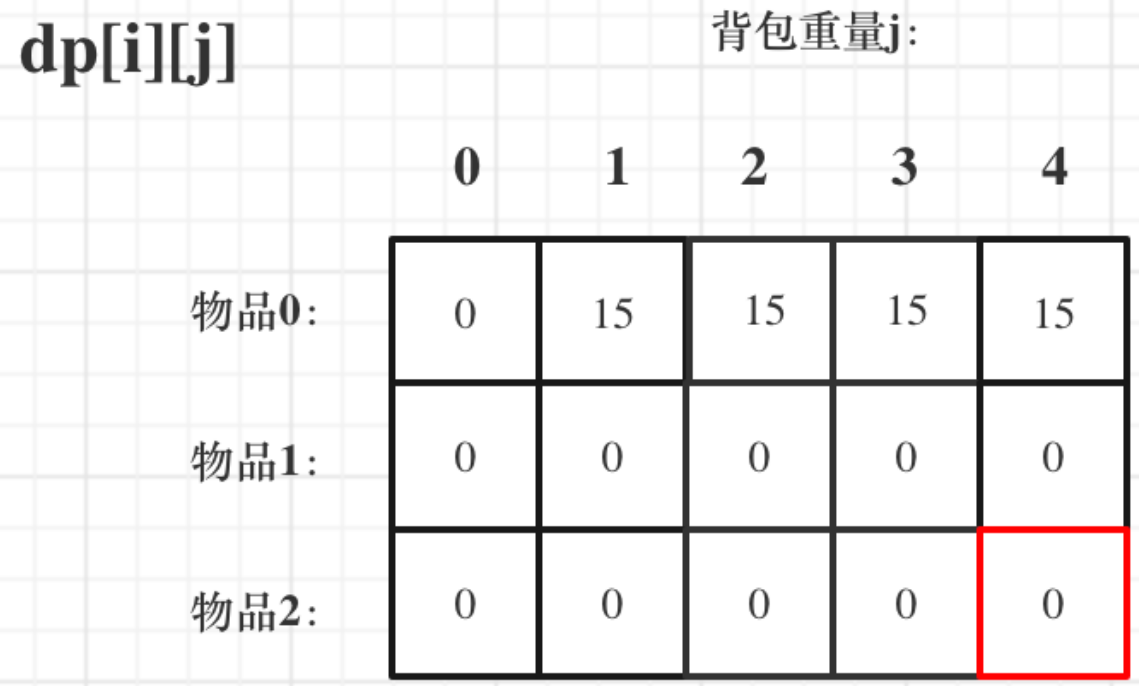
首先從dp[i][j]的定義出發,如果揹包容量j為0的話,即dp[i][0],無論是選取哪些物品,揹包價值總和一定為0。如圖:
在看其他情況。
狀態轉移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推導出來,那麼i為0的時候就一定要初始化。
dp[0][j],即:i為0,存放編號0的物品的時候,各個容量的揹包所能存放的最大價值。
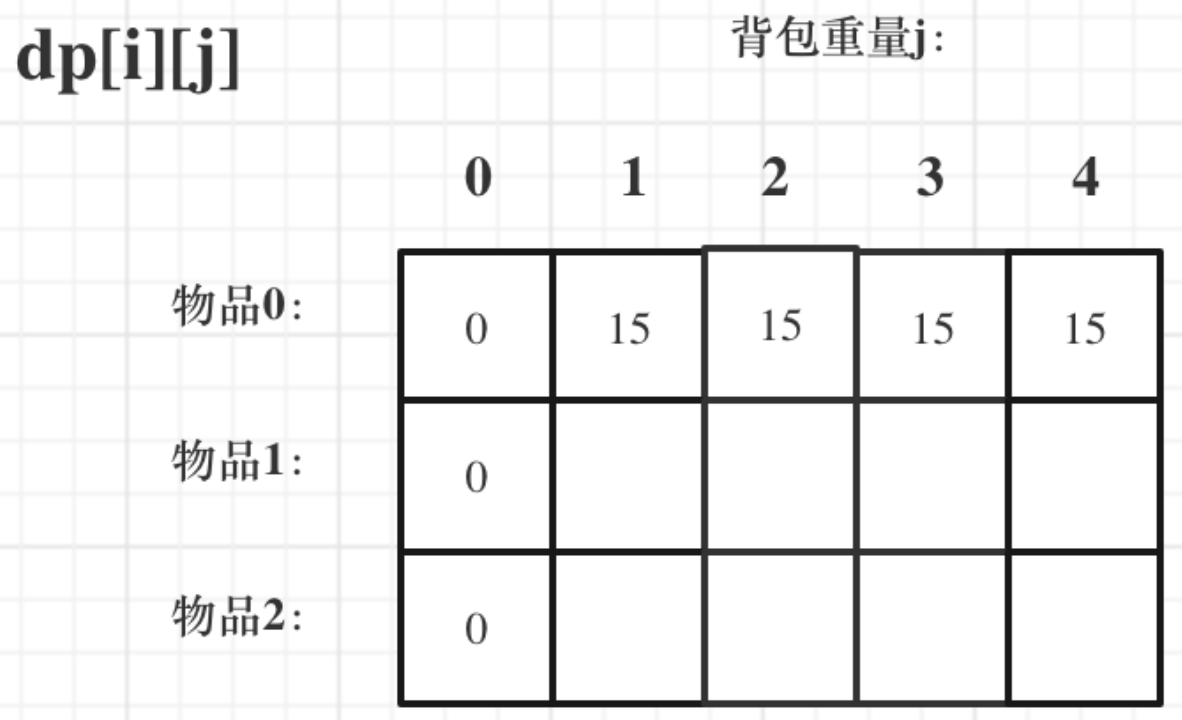
那麼很明顯當 j < weight[0]的時候,dp[0][j] 應該是 0,因為揹包容量比編號0的物品重量還小。
當j >= weight[0]時,dp[0][j] 應該是value[0],因為揹包容量放足夠放編號0物品。
代碼初始化如下:
for (int j = 0 ; j < weight[0]; j++) { // 當然這一步,如果把dp數組預先初始化為0了,這一步就可以省略,但很多同學應該沒有想清楚這一點。
dp[0][j] = 0;
}
// 正序遍歷
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
此時dp數組初始化情況如圖所示:
dp[0][j] 和 dp[i][0] 都已經初始化了,那麼其他下標應該初始化多少呢?
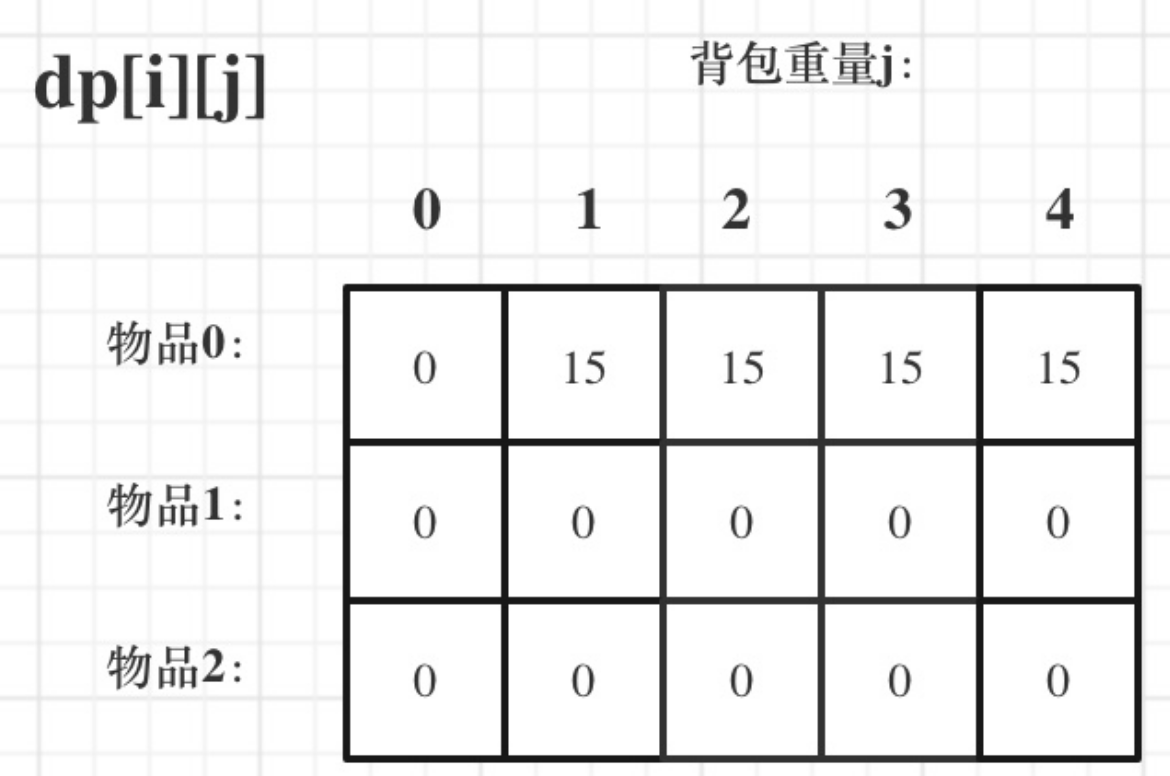
其實從遞歸公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出dp[i][j] 是由左上方數值推導出來了,那麼 其他下標初始為什麼數值都可以,因為都會被覆蓋。
初始-1,初始-2,初始100,都可以!
但只不過一開始就統一把dp數組統一初始為0,更方便一些。如圖:
- 確定遍歷順序
在如下圖中,可以看出,有兩個遍歷的維度:物品與揹包重量
那麼問題來了,先遍歷 物品還是先遍歷揹包重量呢?
其實都可以!! 但是先遍歷物品更好理解。
理解遞歸的本質和遞推的方向。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 遞歸公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推導出來的。
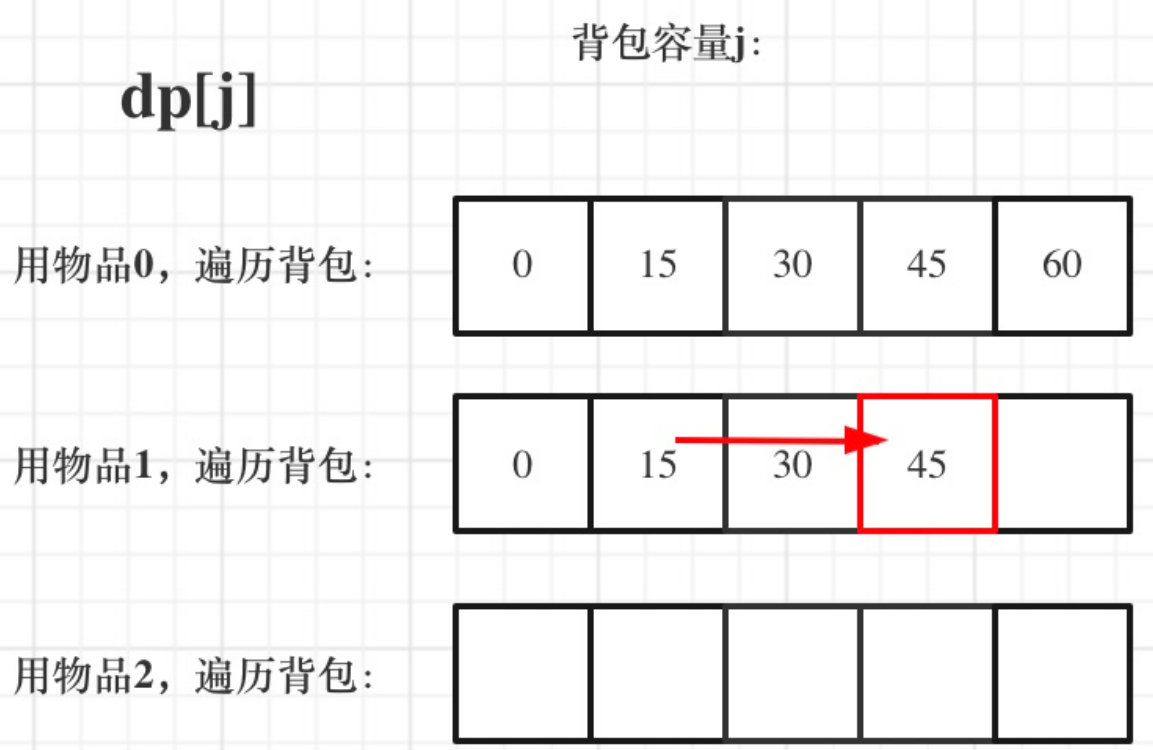
先遍歷物品,再遍歷揹包:
// weight數組的大小 就是物品個數
for(int i = 1; i < weight.size(); i++) { // 遍歷物品
for(int j = 0; j <= bagweight; j++) { // 遍歷揹包容量
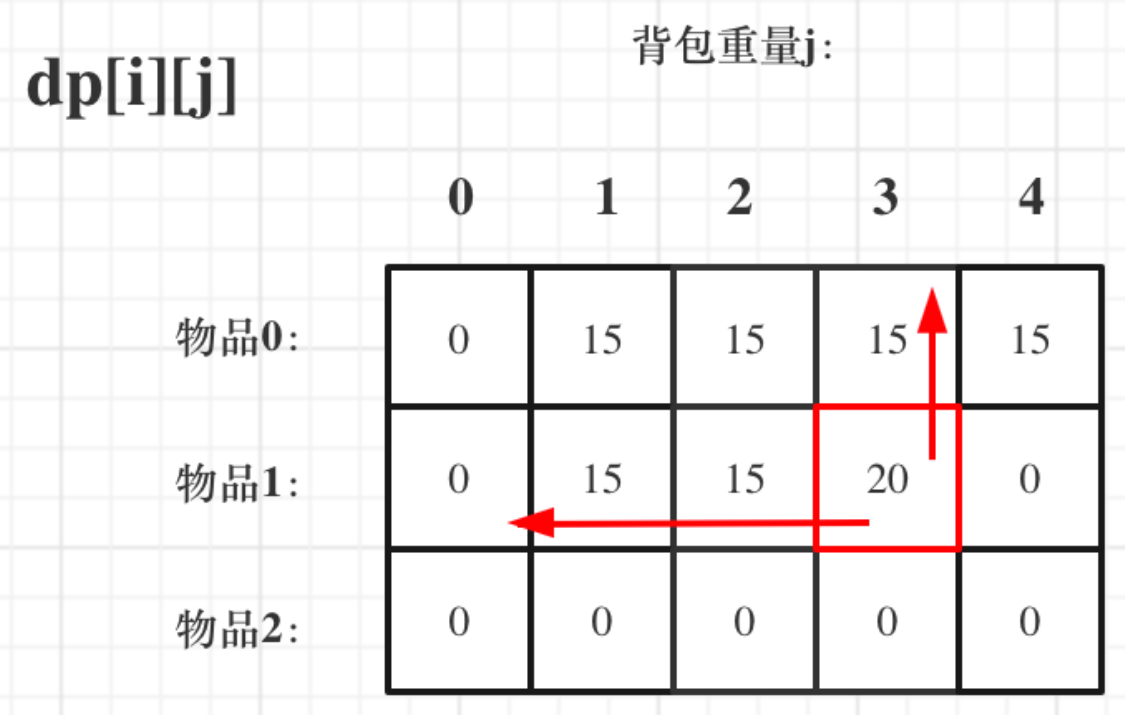
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那麼先遍歷物品,再遍歷揹包的過程如圖所示:
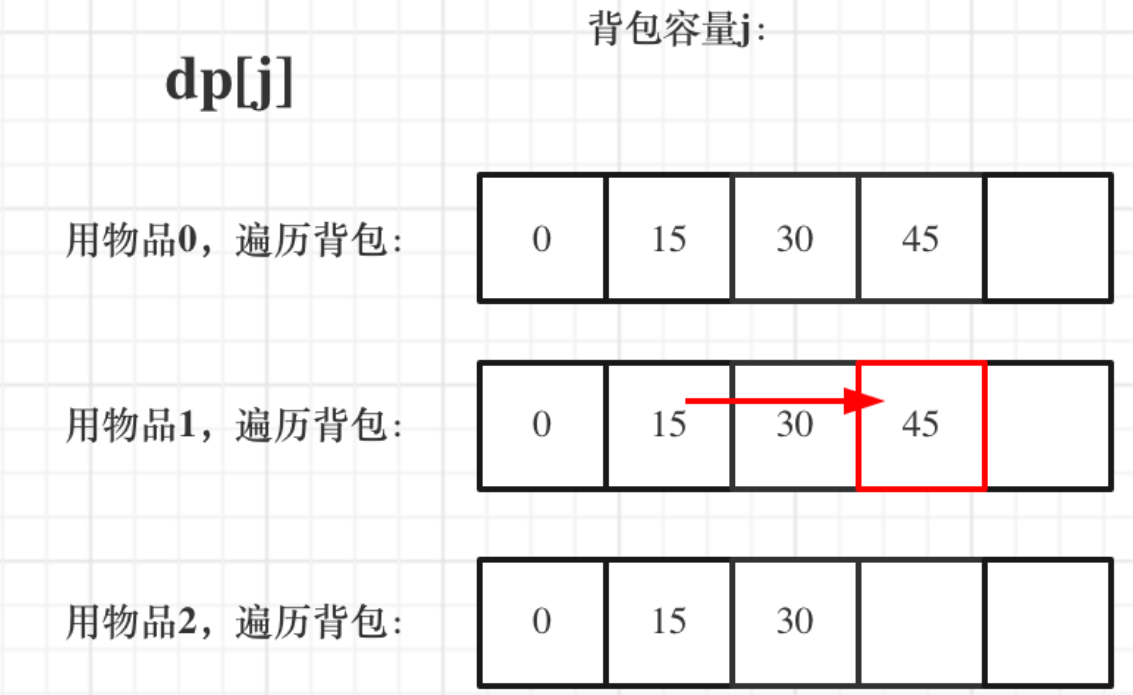
先遍歷揹包,再遍歷物品:
// weight數組的大小 就是物品個數
for(int j = 0; j <= bagweight; j++) { // 遍歷揹包容量
for(int i = 1; i < weight.size(); i++) { // 遍歷物品
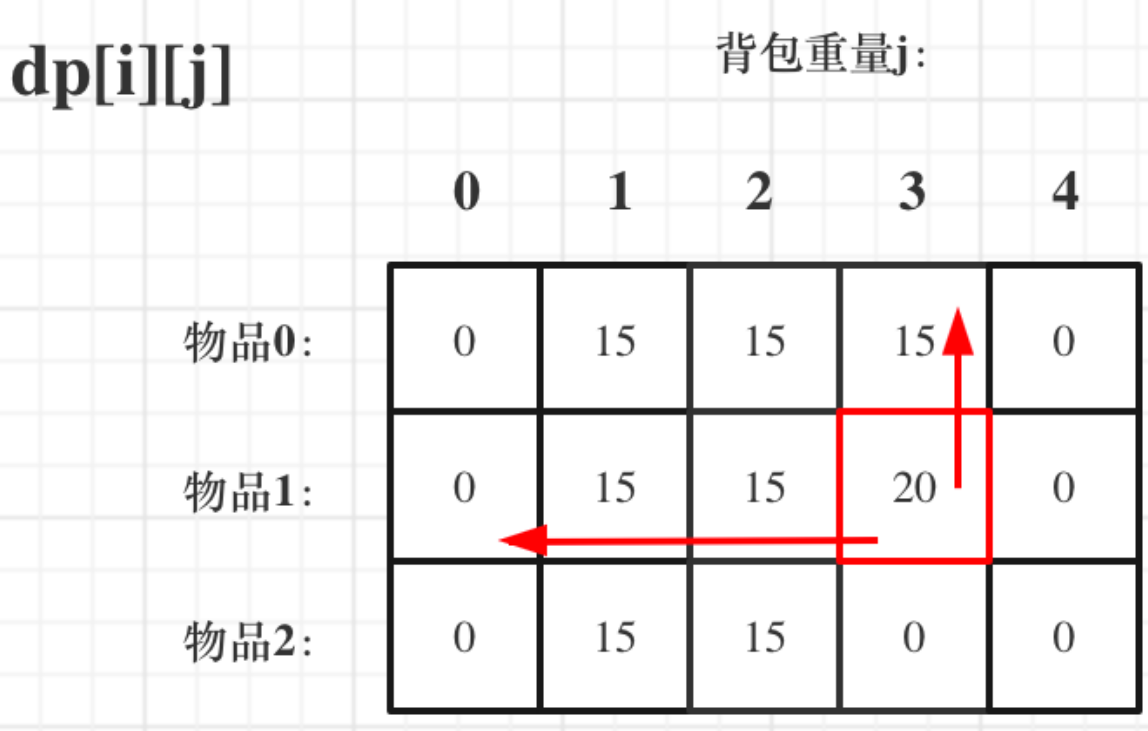
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
先遍歷揹包,再遍歷物品的過程如圖:
可以看出,雖然兩個for循環遍歷的次序不同,但是dp[i][j]所需要的數據就是左上角,根本不影響dp[i][j]公式的推導!
但先遍歷物品再遍歷揹包這個順序更好理解。
- 舉例推導dp數組
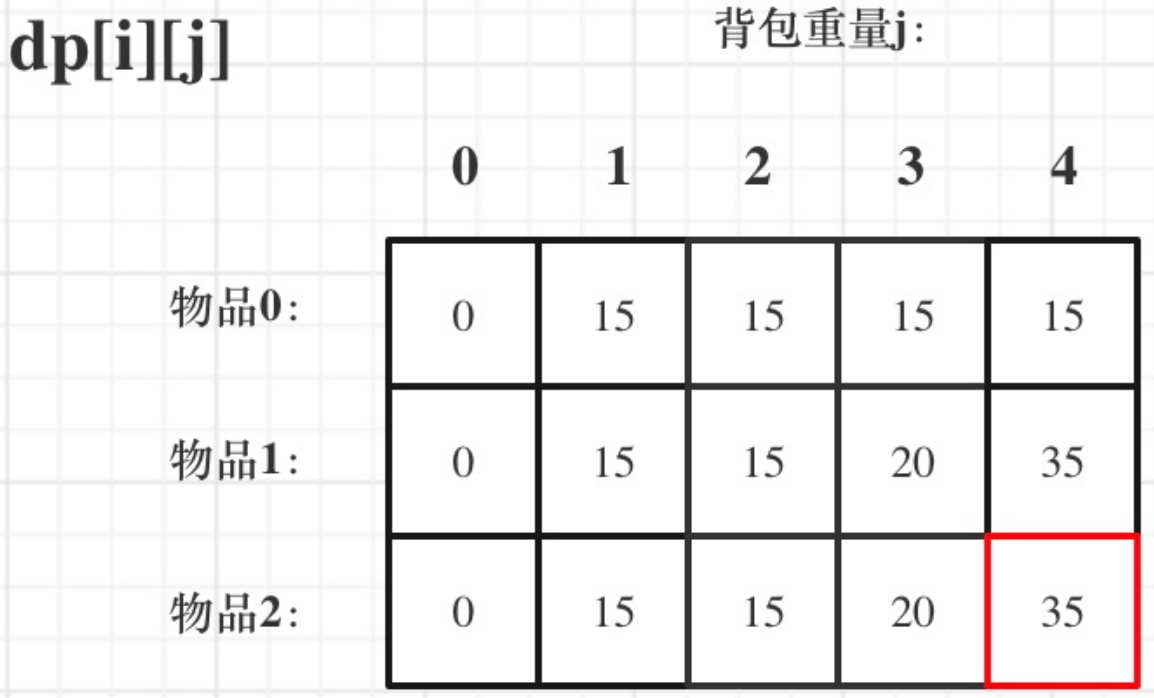
來看一下對應的dp數組的數值,如圖
最後的答案就是dp[2][4]
一維dp數組(滾動數組)
對於揹包問題其實狀態都是可以壓縮的。
在使用二維數組的時候,遞推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其實可以發現如果把dp[i - 1]那一層拷貝到dp[i]上,表達式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
與其把dp[i - 1]這一層拷貝到dp[i]上,不如只用一個一維數組了,只用dp[j](一維數組,也可以理解是一個滾動數組)。
這就是滾動數組的由來,需要滿足的條件是上一層可以重複利用,直接拷貝到當前層。
dp[i][j] 表示從下標為[0-i]的物品裏任意取,放進容量為j的揹包,價值總和最大是多少。
動規五部曲分析如下:
- 確定dp數組的定義
在一維dp數組中,dp[j]表示:容量為j的揹包,所背的物品價值可以最大為dp[j]。
- 一維dp數組的遞推公式
dp[j]為 容量為j的揹包所背的最大價值,那麼如何推導dp[j]呢?
dp[j]可以通過dp[j - weight[i]]推導出來,dp[j - weight[i]]表示容量為j - weight[i]的揹包所背的最大價值。
dp[j - weight[i]] + value[i] 表示 容量為 【j - 物品i重量】 的揹包 加上 物品i 的價值。(也就是容量為j的揹包,放入物品i了之後的價值即:dp[j])
此時dp[j]有兩個選擇,一個是取自己dp[j] 相當於 二維dp數組中的dp[i-1][j],即不放物品i,一個是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,畢竟是求最大價值,
所以遞歸公式為:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
可以看出相對於二維dp數組的寫法,就是把dp[i][j]中i的維度去掉了。
- 一維dp數組如何初始化
dp[j]表示:容量為j的揹包,所背的物品價值可以最大為dp[j],那麼dp[0]就應該是0,因為揹包容量為0所背的物品的最大價值就是0。
那麼dp數組除了下標0的位置,初始為0,其他下標應該初始化多少呢?
看一下遞歸公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp數組在推導的時候一定是取價值最大的數,如果題目給的價值都是正整數那麼非0下標都初始化為0就可以了。
這樣才能讓dp數組在遞歸公式的過程中取的最大的價值,而不是被初始值覆蓋了。
那麼我假設物品價值都是大於0的,所以dp數組初始化的時候,都初始為0就可以了。
- 一維dp數組遍歷順序
代碼如下:
for(int i = 0; i < weight.size(); i++) { // 遍歷物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍歷揹包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
這裏發現和二維dp的寫法中,遍歷揹包的順序是不一樣的!二維dp遍歷的時候,揹包容量是從小到大,而一維dp遍歷的時候,揹包是從大到小。為什麼呢?
倒序遍歷是為了保證物品i只被放入一次!。但如果一旦正序遍歷了,那麼物品0就會被重複加入多次!
舉一個例子:物品0的重量weight[0] = 1,價值value[0] = 15
如果正序遍歷
-
dp[1] = dp[1 - weight[0]] + value[0] = 15
-
dp[2] = dp[2 - weight[0]] + value[0] = 30
此時dp[2]就已經是30了,意味着物品0,被放入了兩次,所以不能正序遍歷。
為什麼倒序遍歷,就可以保證物品只放入一次呢?
倒序就是先算dp[2]
-
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp數組已經都初始化為0)
-
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以從後往前循環,每次取得狀態不會和之前取得狀態重合,這樣每種物品就只取一次了。
那麼問題又來了,為什麼二維dp數組遍歷的時候不用倒序呢?
因為對於二維dp,dp[i][j]都是通過上一層即dp[i - 1][j]計算而來,本層的dp[i][j]並不會被覆蓋!
再來看看兩個嵌套for循環的順序,代碼中是先遍歷物品嵌套遍歷揹包容量,那可不可以先遍歷揹包容量嵌套遍歷物品呢?
不可以!
因為一維dp的寫法,揹包容量一定是要倒序遍歷(原因上面已經講了),如果遍歷揹包容量放在上一層,那麼每個dp[j]就只會放入一個物品,即:揹包裏只放入了一個物品。
倒序遍歷的原因是,本質上還是一個對二維數組的遍歷,並且右下角的值依賴上一層左上角的值,因此需要保證左邊的值仍然是上一層的,從右向左覆蓋。
- 舉例推導dp數組
一維dp,分別用物品0,物品1,物品2 來遍歷揹包,最終得到結果如下:
完全揹包問題
題目描述:有N件物品和一個最多能背重量為W的揹包。第i件物品的重量是weight[i],得到的價值是value[i] 。每件物品都有無限個(也就是可以放入揹包多次),求解將哪些物品裝入揹包裏物品價值總和最大。
完全揹包和01揹包問題唯一不同的地方就是,每種物品有無限件。
例子同上,但每個物品有無數個,其實也就是可以重複取同一個物品。問揹包能背的物品最大價值是多少?
我們知道 01揹包內嵌的循環是從大到小遍歷,為了保證每個物品僅被添加一次。
而完全揹包的物品是可以添加多次的,所以要從小到大去遍歷,即:
// 先遍歷物品,再遍歷揹包
for(int i = 0; i < weight.size(); i++) { // 遍歷物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍歷揹包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
但是 為什麼遍歷物品在外層循環,遍歷揹包容量在內層循環?難道就不能遍歷揹包容量在外層,遍歷物品在內層?
01揹包中二維dp數組的兩個for遍歷的先後循序是可以顛倒了,一維dp數組的兩個for循環先後循序一定是先遍歷物品,再遍歷揹包容量。
在完全揹包中,對於一維dp數組來説,其實兩個for循環嵌套順序是無所謂的!
因為dp[j] 是根據 下標j之前所對應的dp[j]計算出來的。 只要保證下標j之前的dp[j]都是經過計算的就可以了。
遍歷物品在外層循環,遍歷揹包容量在內層循環,狀態如圖:
遍歷揹包容量在外層循環,遍歷物品在內層循環,狀態如圖:
看了這兩個圖,大家就會理解,完全揹包中,兩個for循環的先後循序,都不影響計算dp[j]所需要的值(這個值就是下標j之前所對應的dp[j])。
先遍歷揹包再遍歷物品,代碼如下:
// 先遍歷揹包,再遍歷物品
for(int j = 0; j <= bagWeight; j++) { // 遍歷揹包容量
for(int i = 0; i < weight.size(); i++) { // 遍歷物品
if (j - weight[i] >= 0)
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
多重揹包問題
題目描述:有N種物品和一個容量為V 的揹包。第i種物品最多有Mi件可用,每件耗費的空間是Ci ,價值是Wi 。求解將哪些物品裝入揹包可使這些物品的耗費的空間 總和不超過揹包容量,且價值總和最大。
多重揹包和01揹包是非常像的, 為什麼和01揹包像呢?每件物品最多有Mi件可用,把Mi件攤開,其實就是一個01揹包問題了。
例如:
揹包最大重量為10。
物品為:
| 重量 | 價值 | 數量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
問揹包能背的物品最大價值是多少?
和如下情況有區別麼?
| 重量 | 價值 | 數量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫無區別,這就轉成了一個01揹包問題了,且每個物品只用一次。
代碼如下:
int[] dp = new int[bagWeight + 1];
//先遍歷物品再遍歷揹包,作為01揹包處理
for (int i = 0; i < n; i++) {
for (int j = bagWeight; j >= weight[i]; j--) {
//遍歷每種物品的個數
for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) {
dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);
}
}
}