題⽬描述

輸⼊兩個鏈表，找出它們的第⼀個公共結點。（注意因為傳⼊數據是鏈表，所以錯誤測試數據的提示是⽤其他⽅式顯示的，保證傳⼊數據是正確的）

思路及解答

HashSet包含法

第⼀種做法，直接依賴於 HashSet ，遍歷第⼀個鏈表的時候，將所有的節點，添加到 hashset 中，

遍歷第⼆個鏈表的時候直接判斷是否包含即可，屬於空間換時間的做法。

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        if (pHead1 == null || pHead2 == null) return null;
        
        // 使用HashSet存儲第一個鏈表的所有節點
        HashSet<ListNode> visited = new HashSet<>();
        
        // 遍歷第一個鏈表，將所有節點加入集合
        ListNode current = pHead1;
        while (current != null) {
            visited.add(current);
            current = current.next;
        }
        
        // 遍歷第二個鏈表，檢查節點是否在集合中
        current = pHead2;
        while (current != null) {
            if (visited.contains(current)) {
                return current; // 找到第一個公共節點
            }
            current = current.next;
        }
        
        return null; // 沒有公共節點
    }

• ​時間複雜度​：O(m+n)，需要遍歷兩個鏈表各一次
• ​空間複雜度​：O(min(m,n))，存儲較短鏈表的節點

雙棧法

利用棧的後進先出特性，從鏈表尾部開始比較，找到最後一個相同的節點。公共節點之後的節點都是相同的，所以從後往前比較，最後一個相同的節點就是第一個公共節點

import java.util.Stack;

public class Solution {
    /**
     * 使用雙棧查找兩個鏈表的第一個公共節點
     * 思路：將兩個鏈表分別壓入棧中，然後同時出棧比較
     * 時間複雜度：O(m+n)，空間複雜度：O(m+n)
     */
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        if (pHead1 == null || pHead2 == null) return null;
        
        Stack<ListNode> stack1 = new Stack<>();
        Stack<ListNode> stack2 = new Stack<>();
        
        // 將兩個鏈表的所有節點分別壓入棧中
        ListNode current = pHead1;
        while (current != null) {
            stack1.push(current);
            current = current.next;
        }
        
        current = pHead2;
        while (current != null) {
            stack2.push(current);
            current = current.next;
        }
        
        ListNode commonNode = null;
        
        // 同時從兩個棧彈出節點進行比較
        while (!stack1.isEmpty() && !stack2.isEmpty()) {
            ListNode node1 = stack1.pop();
            ListNode node2 = stack2.pop();
            
            if (node1 == node2) {
                commonNode = node1; // 記錄公共節點
            } else {
                break; // 遇到不同節點，停止比較
            }
        }
        
        return commonNode;
    }
}

• 時間複雜度​：O(m+n)，需要遍歷兩個鏈表各兩次（壓棧和出棧）
• ​空間複雜度​：O(m+n)，需要兩個棧存儲所有節點

長度差法（推薦）

可以將兩個鏈表想象為兩段路程，公共節點是終點。讓長的鏈表先走多出的距離，然後同時前進，就能同時到達公共節點

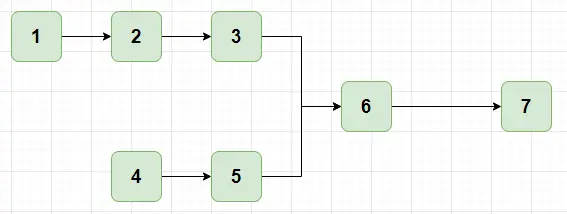
譬如現在有⼀個鏈表 1->2->3->6->7 ，另外⼀個鏈表 4->5->6->7 ，明顯可以看出第⼀個公共節點是6 。

最直接的⽅法，每⼀個鏈表都遍歷⼀次，計算鏈表中的個數，⽐如 1->2->3->6->7 個數為5， 4->5-\>6->7 個數為4，兩者相差1（設為k）個。

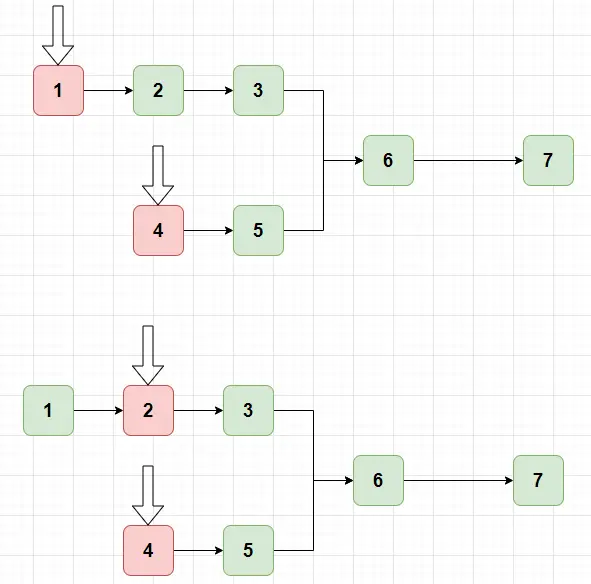
我們可以使⽤兩個指針，分別指向鏈表的頭部。然後讓第⼀個鏈表的指針先⾛ k=1 步。

這樣就相當於指針後⾯的兩個鏈表等⻓了。

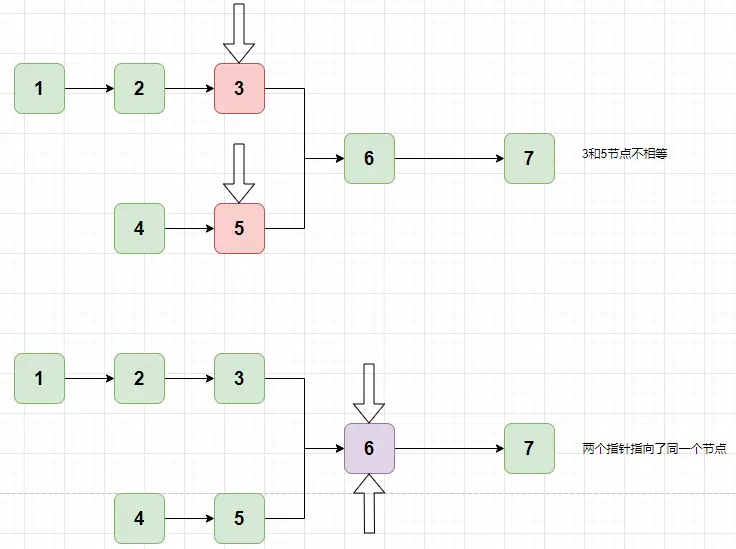
就可以開始⽐較，如果不相等，則兩個指針都往後移動即可，知道節點為null。

/*
public class ListNode {
 int val;
 ListNode next = null;
 ListNode(int val) {
 this.val = val;
 }
}*/
public class Solution {
     public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
         // 只要有⼀個為空，就不存在共同節點
         if (pHead1 == null || pHead2 == null) {
             return null;
         }
         // 計算鏈表1中的節點個數
         int numOfListNode1 = 0;
         ListNode head1 = pHead1;
         while (head1 != null) {
             numOfListNode1++;
             head1 = head1.next;
         }
         
         // 計算鏈表2中節點個數
         int numOfListNode2 = 0;
         ListNode head2 = pHead2;
         while (head2 != null) {
             numOfListNode2++;
             head2 = head2.next;
         }
         
         // ⽐較兩個鏈表的⻓度
         int step = numOfListNode1 - numOfListNode2;
         if (step > 0) {
             // 鏈表1更⻓，鏈表1移動
             while (step != 0) {
                 pHead1 = pHead1.next;
                 step--;
             }
         } else {
             // 鏈表2更⻓，鏈表2移動
             while (step != 0) {
                 pHead2 = pHead2.next;
                 step++;
             }
         }
         
         // 循環遍歷後⾯的節點，相等則返回
         while (pHead1 != null && pHead2 != null) {
             if (pHead1 == pHead2) {
                 return pHead1;
             } else {
                 pHead1 = pHead1.next;
                 pHead2 = pHead2.next;
             }
         }
         return null;
     }
}

• 時間複雜度​：O(m+n)，需要遍歷鏈表三次（兩次計算長度，一次查找）
• ​空間複雜度​：O(1)，只使用常數級別額外空間

但是上⾯的做法，如果公共節點在最後⼀個，假設⼀個鏈表⻓度為 n ，⼀個為 m ，那麼計算個數就要全部遍歷，需要 n+m 。兩個鏈表都移動，到最後⼀個節點的時候才相等，也是 n+m ，也就是 O(2*(n+m)) 。

雙指針遍歷法（最優）

有沒有更加好⽤的做法呢？肯定有，我們來看：

兩個鏈表分別是：

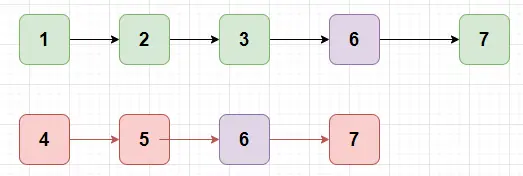
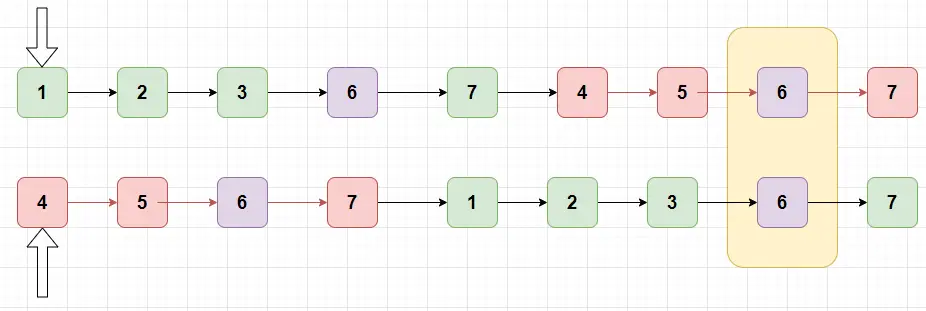
如果我在第⼀個鏈表後⾯拼接上第⼆個鏈表，第⼆個鏈表後⾯拼接上第⼀個鏈表，就會變成下⾯的樣⼦：

發現了⼀個規律，也就是拼接之後的鏈表，是等⻓度的，第⼀個和第⼆個鏈表都從第⼀個開始⽐較，只要相等，就説明是第⼀個公共節點。也就是上⾯被圈起來的 6 節點。

原理如下：

• 設鏈表1獨有部分長度為a，鏈表2獨有部分長度為b，公共部分長度為c
• 指針p1路徑：a + c + b
• 指針p2路徑：b + c + a
• 兩個指針路徑長度相同，會在公共節點相遇

特殊情況處理：​​當兩個鏈表沒有公共節點時，兩個指針會同時變為null，退出循環

public class Solution {
     public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
         // 只要有⼀個為空，就不存在共同節點
         if (pHead1 == null || pHead2 == null) {
             return null;
         }
         
         ListNode head1 = pHead1;
         ListNode head2 = pHead2;
         while (head1 !=head2) {
             // 如果下⼀個節點為空，則切換到另⼀個鏈表的頭節點，否則下⼀個節點
             head1 = (head1 == null) ? pHead2 : head1.next;
             head2 = (head2 == null) ? pHead1 : head2.next;
         }
         return head1;
     }
}

• 時間複雜度​：O(m+n)，每個指針遍歷兩個鏈表各一次
• ​空間複雜度​：O(1)，只使用兩個指針