介紹

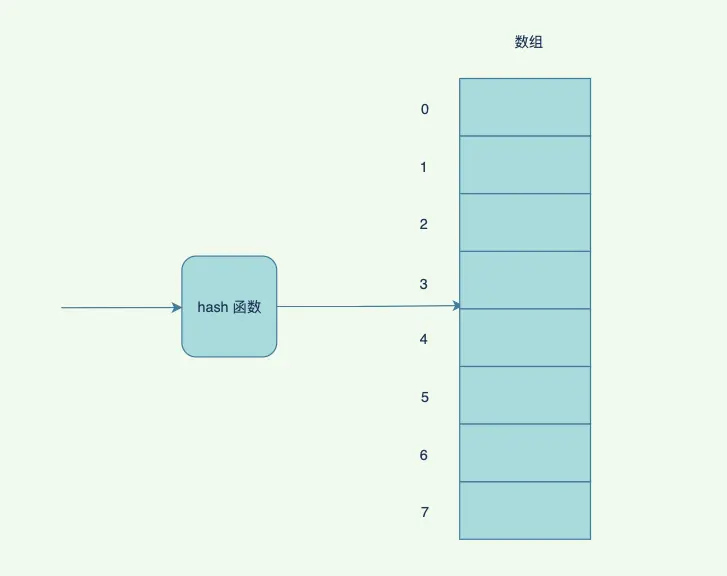
像線性數據結構在查找的時候，⼀般都是使⽤= 或者!= ，在折半查找或者其他範圍查詢的時候，可能會使⽤< 和> ,理想的時候，我們肯定希望不經過任何的⽐較，直接能定位到某個位置（存儲位置），這種在數組中，可以通過索引取得元素。那麼，如果我們將需要存儲的數據和數組的索引對應起來，並且是⼀對⼀的關係，那不就可以很快定位到元素的位置了麼？

只要通過函數f(k) 就能找到k 對應的位置，這個函數f(k) 就是hash 函數。它表示的是⼀種映射關係，但是對不同的值，可能會映射到同⼀個值（同⼀個hash 地址），也就是f(k1) = f(k2) ，這種現象我們稱之為衝突或者碰撞。

hash 表定義如下：散列表（Hash table，也叫哈希表），是根據鍵（Key）⽽直接訪問在內存儲存位置的數據結構。也就是説，它通過計算⼀個關於鍵值的函數，將所需查詢的數據映射到表中⼀個位置來訪問記錄，這加快了查找速度。這個映射函數稱做散列函數，存放記錄的數組稱做散列表。

⼀般常⽤的hash 函數有：

• 直接定址法：取出關鍵字或者關鍵字的某個線性函數的值為哈希函數，⽐如H(key) = key 或者H(key) = a * key + b
• 數字分析法：對於可能出現的數值全部瞭解，取關鍵字的若⼲數位組成哈希地址
• 平⽅取中法：取關鍵字平⽅後的中間⼏位作為哈希地址
• 摺疊法：將關鍵字分割成為位數相同的⼏部分（最後⼀部分的位數可以不同），取這⼏部分的疊加和（捨去進位），作為哈希地址。
• 除留餘數法：取關鍵字被某個不⼤於散列表表⻓m 的數p 除後所得的餘數為散列地址。即h ash(k)=k mod p ， p< =m 。不僅可以對關鍵字直接取模，也可在摺疊法、平⽅取中法等運算之後取模。對p 的選擇很重要，⼀般取素數或m ，若p 選擇不好，容易產⽣衝突。
• 隨機數法：取關鍵字的隨機函數值作為它的哈希地址。

但是這些⽅法，都⽆法避免哈希衝突，只能有意識的減少。那處理hash 衝突，⼀般有哪些⽅法呢？

解決哈希衝突的三種方法

拉鍊法、開放地址法、再散列法

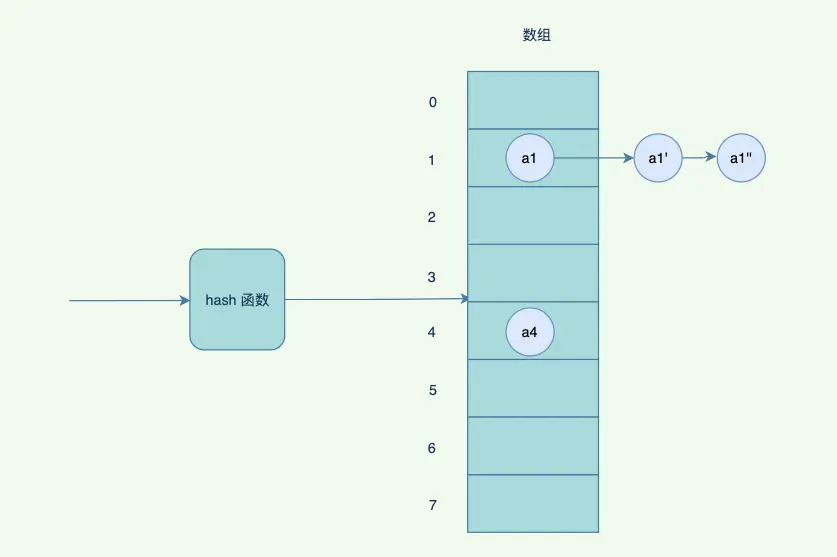
拉鍊法

HashMap，HashSet其實都是採用的拉鍊法來解決哈希衝突的，就是在每個位桶實現的時候，採用鏈表的數據結構來去存取發生哈希衝突的輸入域的關鍵字（也就是被哈希函數映射到同一個位桶上的關鍵字）

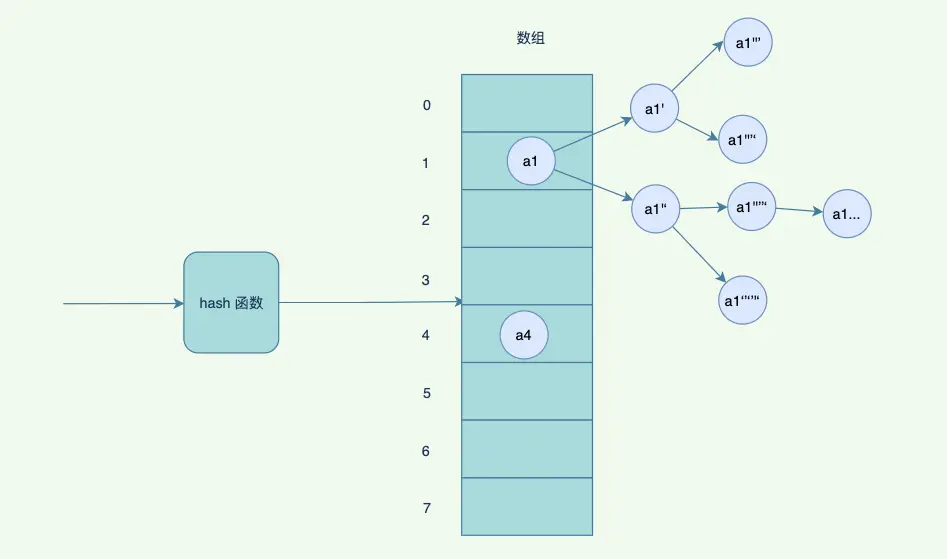
但是如果hash 衝突⽐較嚴重，鏈表會⽐較⻓，查詢的時候，需要遍歷後⾯的鏈表，因此JDK 優化了⼀版，鏈表的⻓度超過閾值的時候，會變成紅⿊樹，紅⿊樹有⼀定的規則去平衡⼦樹，避免退化成為鏈表，影響查詢效率。

但是你肯定會想到，如果數組太⼩了，放了⽐較多數據了，怎麼辦？再放衝突的概率會越來越⾼，其實這個時候會觸發⼀個擴容機制，將數組擴容成為 2 倍⼤⼩，重新hash 以前的數據，哈希到不同的數組中。

hash 表的優點是查找速度快，但是如果不斷觸發重新 hash , 響應速度也會變慢。同時，如果希望範圍查詢， hash 表不是好的選擇。

拉鍊法的裝載因子為n/m（n為輸入域的關鍵字個數，m為位桶的數目）

開放地址法

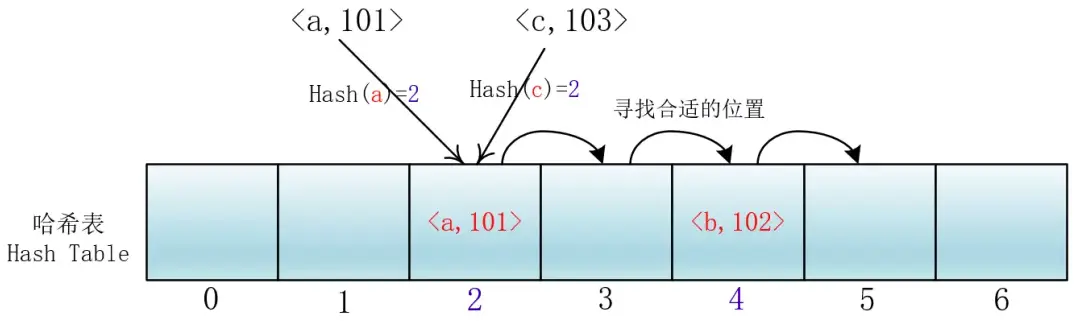
所謂開放地址法就是發生衝突時在散列表（也就是數組裏）裏去尋找合適的位置存取對應的元素，就是所有輸入的元素全部存放在哈希表裏。也就是説，位桶的實現是不需要任何的鏈表來實現的，換句話説，也就是這個哈希表的裝載因子不會超過1。

它的實現是在插入一個元素的時候，先通過哈希函數進行判斷，若是發生哈希衝突，就以當前地址為基準，根據再尋址的方法（探查序列），去尋找下一個地址，若發生衝突再去尋找，直至找到一個為空的地址為止。

探查序列的方法:

• 線性探查
• 平方探測
• 偽隨機探測

線性探查

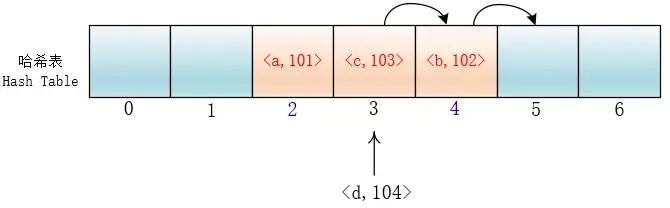
di =1，2，3，…，m-1；這種方法的特點是：衝突發生時，順序查看錶中下一單元，直到找出一個空單元或查遍全表。

（使用例子：ThreadLocal裏面的ThreadLocalMap中的set方法）

private void set(ThreadLocal<?> key, Object value) {

    // We don't use a fast path as with get() because it is at
    // least as common to use set() to create new entries as
    // it is to replace existing ones, in which case, a fast
    // path would fail more often than not.

    Entry[] tab = table;
    int len = tab.length;
    int i = key.threadLocalHashCode & (len-1);

    //線性探測的關鍵代碼
    for (Entry e = tab[i];
         e != null;
         e = tab[i = nextIndex(i, len)]) {
        ThreadLocal<?> k = e.get();

        if (k == key) {
            e.value = value;
            return;
        }

        if (k == null) {
            replaceStaleEntry(key, value, i);
            return;
        }
    }

    tab[i] = new Entry(key, value);
    int sz = ++size;
    if (!cleanSomeSlots(i, sz) && sz >= threshold)
        rehash();
}

但是這樣會有一個問題，就是隨着鍵值對的增多，會在哈希表裏形成連續的鍵值對。當插入元素時，任意一個落入這個區間的元素都要一直探測到區間末尾，並且最終將自己加入到這個區間內。這樣就會導致落在區間內的關鍵字Key要進行多次探測才能找到合適的位置，並且還會繼續增大這個連續區間，使探測時間變得更長，這樣的現象被稱為“一次聚集（primary clustering）”。

平方探測

在探測時不一個挨着一個地向後探測，可以跳躍着探測，這樣就避免了一次聚集。

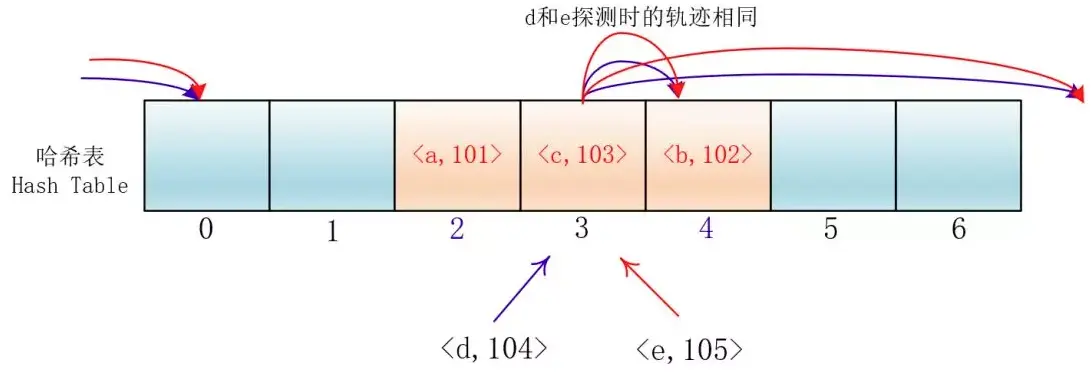
di=12，-12，22，-22，…，k2，-k2；這種方法的特點是：衝突發生時，在表的左右進行跳躍式探測，比較靈活。雖然平方探測法解決了線性探測法的一次聚集，但是它也有一個小問題，就是關鍵字key散列到同一位置後探測時的路徑是一樣的。這樣對於許多落在同一位置的關鍵字而言，越是後面插入的元素，探測的時間就越長。

這種現象被稱作“二次聚集(secondary clustering)”,其實這個在線性探測法裏也有。

偽隨機探測

di=偽隨機數序列；具體實現時，應建立一個偽隨機數發生器，（如i=(i+p) % m），生成一個位隨機序列，並給定一個隨機數做起點，每次去加上這個偽隨機數++就可以了。

再散列法

再散列法其實很簡單，就是再使用哈希函數去散列一個輸入的時候，輸出是同一個位置就再次散列，直至不發生衝突位置

缺點：每次衝突都要重新散列，計算時間增加。一般不用這種方式