乾貨分享：可證明安全的隱私計算詳情 - 隱私,開源,計算機科學隱語SecretFlow 博客

“隱語”是開源的可信隱私計算框架，內置 MPC、TEE、同態等多種密態計算虛擬設備供靈活選擇，提供豐富的聯邦學習算法和差分隱私機制。

開源項目：
https://github.com/secretflow
https://gitee.com/secretflow

DataFunTalk.專注於大數據、人工智能技術應用的分享與交流。致力於成就百萬數據科學家。定期組織技術分享直播，並整理大數據、推薦/搜索算法、廣告算法、NLP 自然語言處理算法、智能風控、自動駕駛、機器學習/深度學習等技術應用文章。

嘉賓：洪澄

洪澄，中國科學院大學博士，目前於阿里巴巴集團安全部雙子座實驗室擔任資深安全專家，主要從事密碼學、隱私保護計算相關技術研究，帶領團隊在EuroCrypt、S&P(Oakland)、USENIX’SEC、SIGMOD、SIGKDD、VLDB等頂級學術會議和期刊上發表論文30餘篇，獲iDASH國際基因隱私計算大賽一等獎，牽頭負責了安全多方計算國際標準IEEE P2842的撰寫工作。

分享主題：可證明安全的隱私計算

正文：為什麼隱私計算中會需要可證明安全？顧名思義，隱私計算是保護隱私的計算，那麼視隱私保護程度的不同，其計算效率也不同。比如，廣域網下多方合作，使用LR訓練一個這麼大的數據集，迭代一次需要多久呢？有的方案需要 100 秒，有的需要 0.3 秒，有的則需要 15 分鐘。

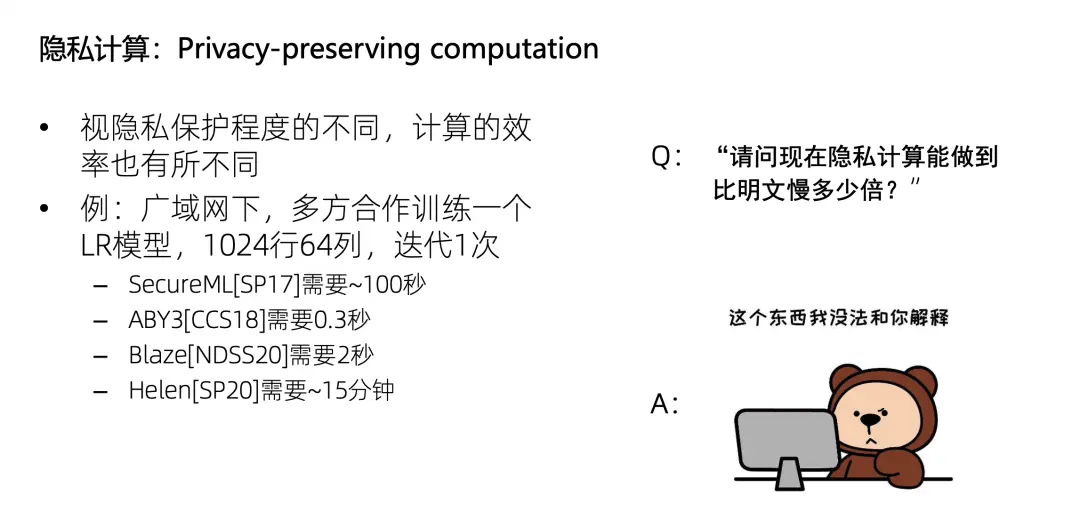
所以如果直接問隱私計算的效率現在能做到比明文慢多少倍，這是沒有辦法回答的；先描述隱私保護的程度，再描述計算效率，這個描述才有意義。例如，我們列一個座標軸，X 軸是效率，Y 軸是安全性，只説效率是多少，就像只給出 X 軸的座標，沒有給出 Y 軸的座標，那是無法判斷這個方案的好壞的。

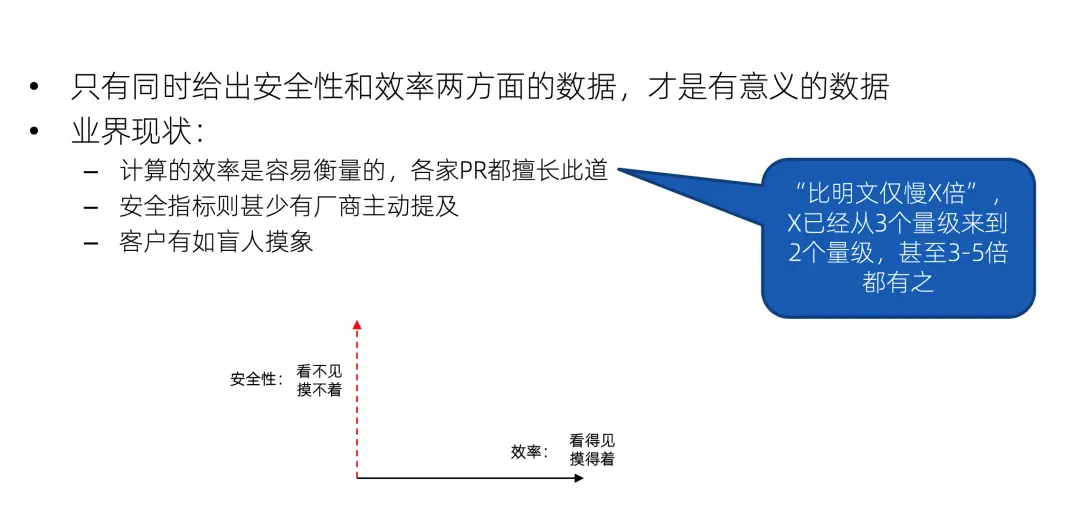
但是因為效率是最容易衡量的，大家都非常擅長 PR 這個X軸，比如能做到僅比明文計算慢多少倍，有的人説三個量級，有的人説兩個量級，甚至我最近看到説比明文僅慢 3 到 5 倍的都有。但是Y軸則甚少有廠商主動提及，因為他看不見摸不着也不好描述。那客户就永遠只能看到 X 軸，猶如盲人摸象，這就是業界的一個現狀。
如何講清楚一個方案在Y軸中的位置？這就需要可證明安全了。首先要明確定義安全假設，即方案能防禦什麼樣的攻擊者，不能防禦什麼樣的攻擊者；然後在這一假設下，證明方案面對攻擊者的時候，能達到什麼樣的防護效果，有哪些信息泄露。打個比方，僅説“我的方案是安全的”，這是不夠的；更合適的方法是證明“我的方案在雙方都是半誠實的假設下，只會泄露行數、列數、建模結果，沒有其他信息泄露”。這樣就可以方便地在Y軸中找到它的位置了。

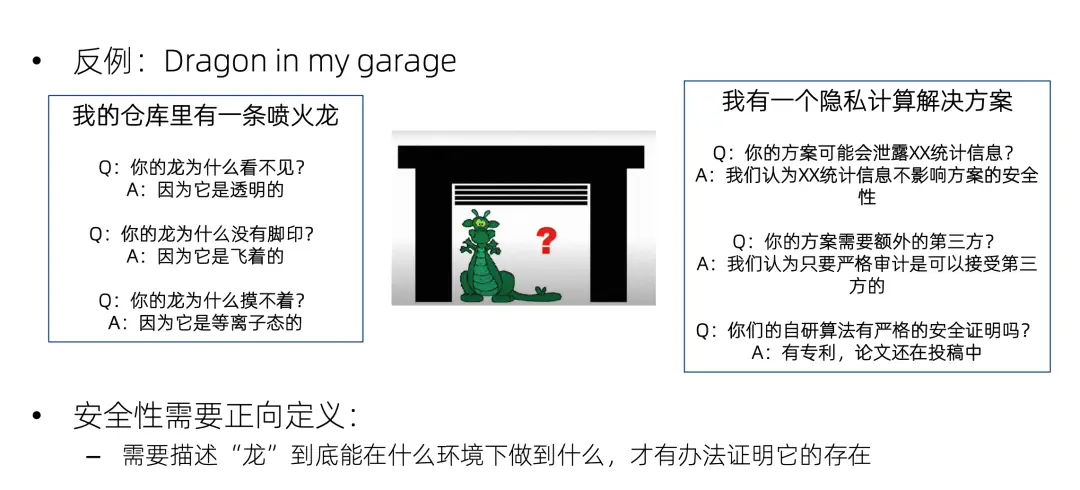
這裏有一個很好的反例，就是 dragon in my garage，這是西方的一個寓言：我的倉庫裏有一條噴火龍。別人問我：你的龍為什麼看不見？我説因為它是透明的。又問：你的龍為什麼沒有腳印？我説因為它是飛着的。又問：你的龍為什麼摸不着？我説因為它是等離子態的。只要我沒有明確地定義什麼是龍，龍能幹什麼，那麼無論你怎麼問，我都可以找到一個圓過去的方法。
隱私計算的安全性也是如此，如果不使用可證明安全來正面的論證一個隱私計算方案的安全性，而是被動地等着別人來挑戰，那就跟倉庫噴火龍一樣，無論怎麼攻擊都可以圓過去。比如別人問我的方案是不是泄露了統計信息？我説這不重要，不影響隱私。又問：方案是不是需要額外的第三方？我説我們會對第三方進行嚴格的審計，又問：你這個自創的加密算法有安全證明嗎？我説為技術保密，暫時不能公佈；等等。

注意一個誤區，就是要求方案具備可證明安全性，並不等於要求方案具備最高級的安全性。因為最高級安全性的代價太高了，在不需要最高級安全性的場合，完全可以降低安全性以提升效率，也就是減小Y座標來獲得大一點的X座標。但是不能只説X座標，而不去説明Y座標犧牲了多少。可證明安全就是一把尺子，用來對Y座標進行嚴格的論證。

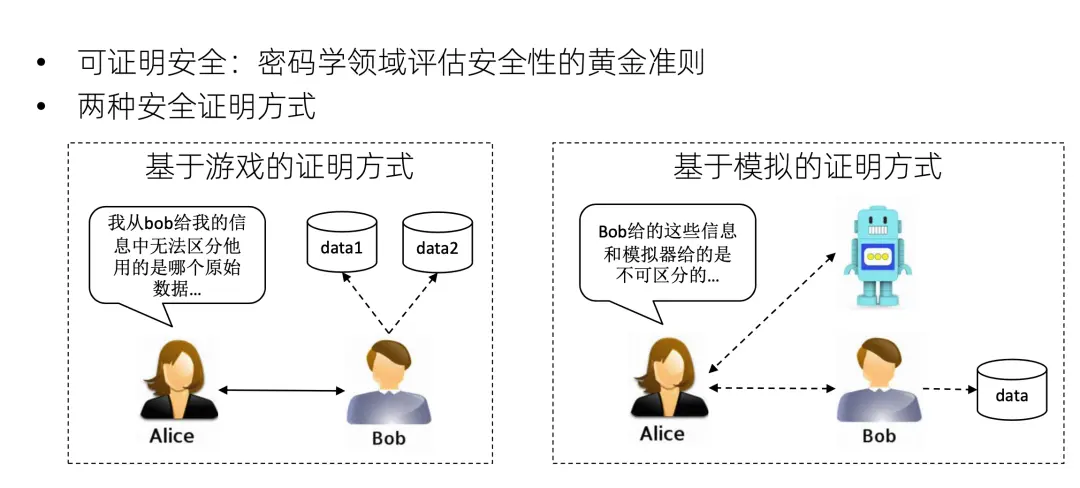
可證明安全是密碼學領域評估算法安全性的黃金準則。目前有兩種流行的證明方式：第一個是基於遊戲的證明方式。通過一個例子來説明什麼是基於遊戲的證明方式。假設 Alice 是攻擊者，Bob是防守者。Bob 跟 Alice 運行一個協議，然後 Bob 挑選兩個數據data 1和 data 2 的其中之一。但是 Alice 從這個交互的協議過程中猜不出來 Bob 用的是 data 1 還是 data 2。如果這對任意 data 1 跟 data 2 都成立的話，就可以説這個協議是安全的，因為這可以説明Alice對Bob的原始數據的信息是一無所知的。
第二個是基於模擬的證明方式。假設 Alice 與兩方交互。第一個是 Bob，它正在運行着自己的真實數據，和 Alice 跑一個真正的隱私計算協議。另一個是個機器人，是個模擬器，它並沒有 Bob 的輸入數據，只有整個計算的結果。Alice 跟這個機器人和 Bob 同時進行交互，它感覺不出來哪個是機器人哪個是 Bob。可以看到，這個機器人根本沒有用Bob的原始數據，Alice都區分不出來。那説明這個協議確實沒有對Alice泄露任何結果之外的信息。

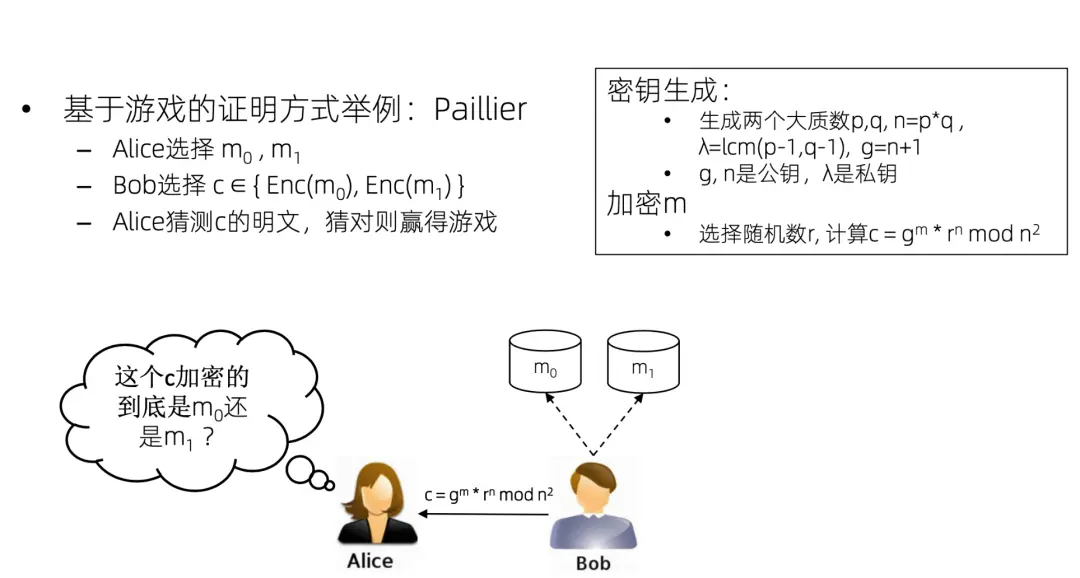
我們通過一個paillier同態加密的例子來理解如何用基於遊戲的證明方式來證明paillier是安全的。
假設Alice是攻擊者，Alice 可以任選兩個數據m0和m1，然後讓 Bob 來加密一下這兩個數據。Bob 加密了這兩個數據，然後從其中任意選了一個，把密文發給 Alice。Alice 去猜到底加密的是 m0 還是 m1。可以看出如果隨便猜的話，那成功的概率一定是50%。但是如果Alice能夠以大於 50% 的概率猜對的話，那説明paillier算法一定有問題。

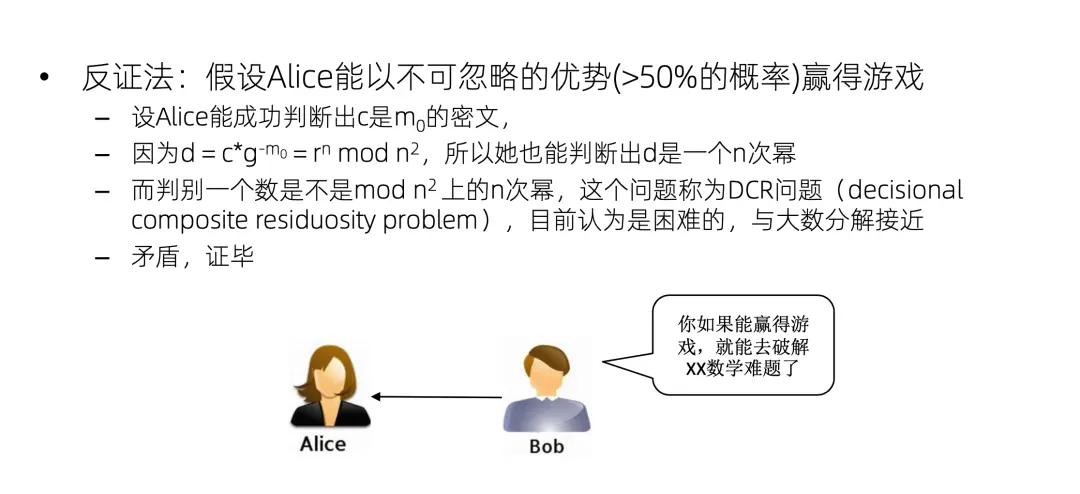
我們來做一個反證，假設Alice可以贏得這個遊戲，能以大於 50% 的概率猜對這個到底是 m0 的密文還是 m1 的密文，我們不妨假設它是 m0 的密文，Alice猜對了。那麼Alice能夠猜出 C 是 m0 的密文，那她就可以把這個 m0 約掉。剩下 r 的 n 次方，也就是 d 是 mod n 平方上的一個 n 次冪，就是Alice可以成功地判斷這樣一個 n 次冪。但是這個判斷叫做 dcr 問題，這個問題是困難的，一般認為它跟大數分解的難度是接近的，所以就產生了矛盾。換句話説，如果 Alice 能夠贏得這個遊戲，那她就可以破解 dcr 問題。所以 Alice 不能夠贏得這個遊戲，也就是説 Alice 只能以 50% 的概率隨機地猜測，即Paillier算法在dcr假設下是安全的。

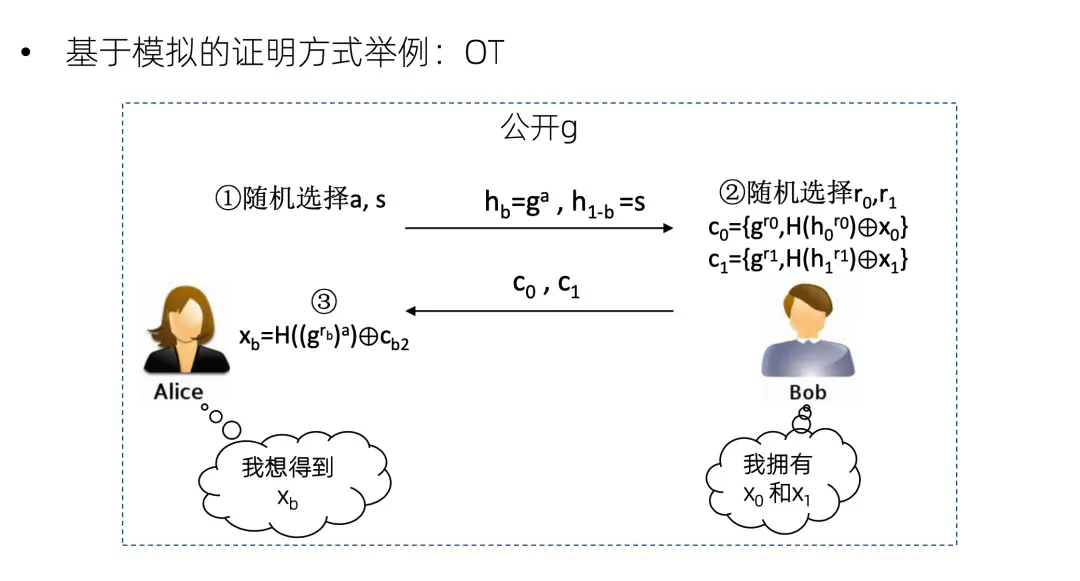
再來看一個基於模擬的證明方式的例子，以一個簡單的OT協議為例。Bob 擁有兩個數 x0 和x1，Alice 想得到其中一個，但她不想告訴 Bob 她想得到哪一個。協議具體內容是Alice隨機選擇 s ，然後發送這兩個數給 Bob ，然後 Bob 就加密這兩個數，發回去。因為Alice有其中一個數的離散對數，所以她可以解密其中一個。但是 Bob 並不知道Alice能解密哪個。我們看如何用基於模擬的證明方式證明這個OT的安全性。

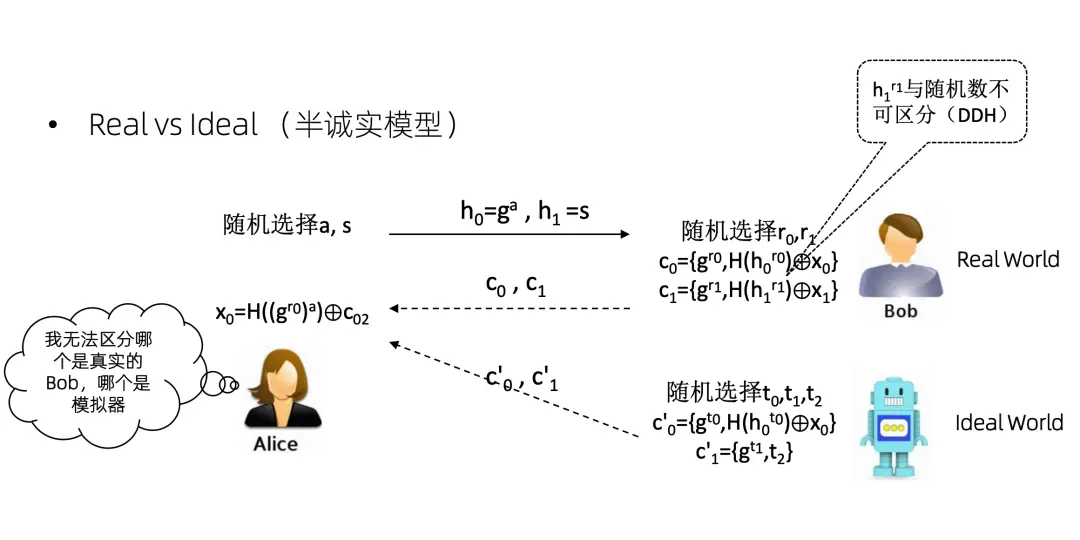
假設Alice是攻擊者。假設存在一個機器人和一個 Bob，Bob 是有真實的數據 x0 和 x1 的，但是機器人沒有，它只有最終的OT計算結果x0，對 x1 是一無所知的。那麼機器人跟 Bob 一樣，也和Alice運行一個協議。因為機器人知道 x0，所以它可以把 x0 加密。然後它不知道x1，那就弄一個隨機數發過去。Alice拿到這個機器人的兩個數，又拿到了 Bob 的兩個數。到底哪兩個數是 Bob 發來的，哪兩個數是模擬器發來的，Alice是區分不出來的。因為這個 h1r1 和隨機數是不可區分的。
這個就叫做 real world 和 ideal world，real world 就是真實在發生的事情。ideal world 就是模擬器在做的事情。基於模擬的證明方式就是證明攻擊者沒辦法區分 real word 和 ideal word。當然這只是半誠實模型，如果是惡意模型，那麼這個證明會非常的複雜，只能説 do not try this at home，把它交給密碼學家去證明。
我們剛才只是證明了一個paillier和OT，那麼如何證明整個方案的安全性？
首先，要證明整個方案的每個部分都是安全的，比如加法是安全的，乘法是安全的，relu是安全的。第二步，要判斷各個模塊的運行方式，如果模塊之間是串行運行的話，那麼整個方案可以滿足可證明安全，因為可證明的安全模塊之間是 sequential composable 的。如果不是串行運行，那還需要每個模塊都滿足 UC 特性才行。這裏不做講解了，對密碼學有興趣的同學可以去看一看。一般的單個建模任務，我們可以認為它是串行的，不需要考慮 UC 的問題。

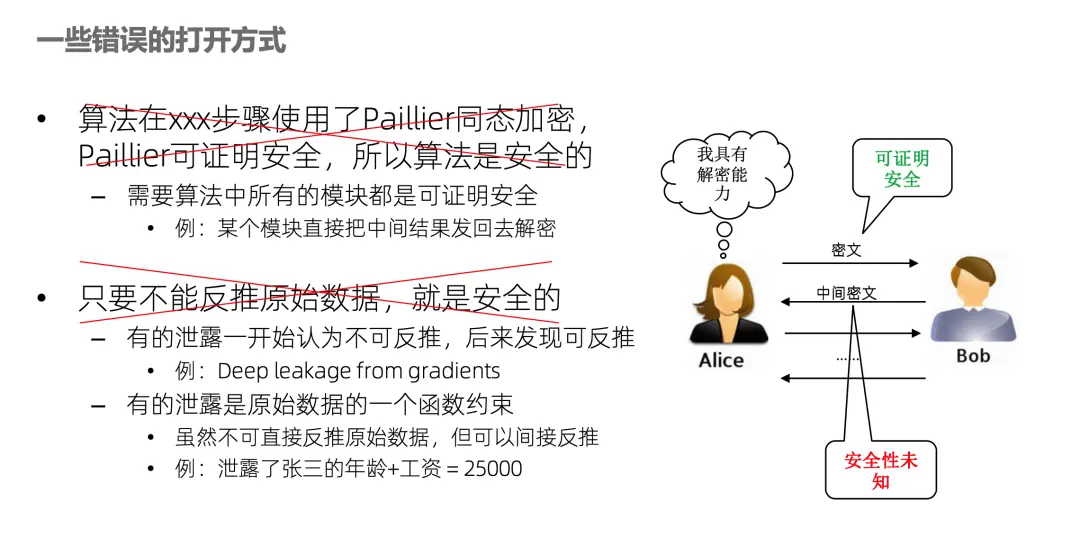
講一下錯誤的打開方式，比如有人説我的算法使用了paillier加密，paillier是可證明安全的，所以我的算法是安全的。這個説法肯定是錯誤的，好比需要大廈的每塊磚都是可證明安全的才行，不能説用了一塊可證明安全的磚，所以整個大廈都是安全的。例如很多聯邦學習算法，中間信息是Alice用 paillier加密發給 Bob，這步是沒問題，但 Bob 計算完之後就發回去Alice解密繼續做其他的計算。這一步解密產生的信息泄露如果沒有論證，其風險就是未知的。
另一個錯誤的打開方式是隻要不能反推原始數據就是安全的。首先一個問題就是很難定義什麼叫反推原始數據，不具可操作性。例如要測試哪些反推算法，這是沒法窮舉的。有的泄露一開始認為不能反推，但過了幾年大家發現可以反推了，比如deep leakage from gradients這篇文章，就是聯邦學習中的梯度，大家開始認為梯度不是原始數據，傳了沒問題。但後來有人發現一種攻擊算法可以從梯度推出原始數據。那如果再防禦一下，給方案打個補丁行不行呢？再保護也只能針對某種特定的攻擊，永遠是道高一尺，魔高一丈，是不可證明的，永遠無法在Y軸中確定方案的位置。只有嚴謹的正向論證，才是可證明安全。
還有一個可能性就是方案確實沒有泄露原始數據，但是泄露了原始數據的一個函數約束。例如攻擊者確實推不出張三的年齡，也推不出張三的工資，但是可以推出張三的年齡和工資之和是25,000。可以看出這個結論已經對攻擊者很有價值了，如果攻擊者將來知道了張三的年齡，工資就出來了；或者攻擊者根本就不需要詳細數值，只需要知道他的工資是在這個範圍就行了。所以僅僅描述“不能反推原始數據”是不夠的，還得把泄露的具體函數約束通過可證明的方式勾畫出來。
有人説這些密碼學證明太難了，還有別的方法可以證明嗎？好消息是有，壞消息是也很難，並不比密碼學可證明容易。這個方法就是差分隱私。差分隱私跟前面的證明方法有一些區別，也有一些聯繫。假設Bob有兩個數據集，兩個數據集的唯一區別是其中一個裏面沒張三，另一個數據集裏面有張三。然後Bob跟 Alice 進行交互。如果對於任意的張三，兩個數據集的交互信息的分佈都非常接近，説明這一交互過程對 Bob 數據集裏所有的行都是保護的，因為Alice連張三在不在裏面都不知道，肯定是推不出張三的信息。

如何實現差分隱私？以DP-SGD 為例，SGD是機器學習裏面的一個梯度下降算法，它對每份訓練數據計算一個梯度，然後把梯度加到模型上去。DP-SGD就是首先把這個梯度裁剪到一個合適的大小，往裏面加上一個noise，之後任意一條數據減掉或者加起來都對總體分佈區別不大了，所以可以滿足差分隱私。DP-SGD計算要比通常的SGD慢一點，因為它要對每條梯度進行裁剪、加噪。在 tensorflow 裏面，它集成了相關的算法，這個算法可以非常容易地用於橫向分割的聯邦學習。

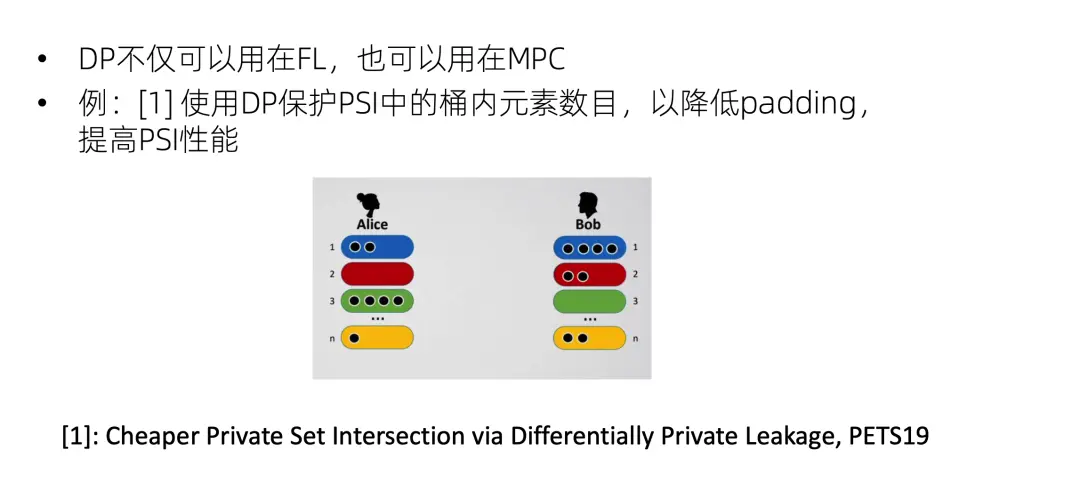
DP也可以用在 MPC，例如PSI隱私求交集，大家可能經常會用到分桶來做 PSI，因為整個全集都跟對方逐個比較性能太低了，所以一般都是分成好幾個桶，比如尾號是 1 的一起比一下，尾號是 2 的一起比一下，這樣會比較快，也便於並行。但是這樣可能會泄露一個信息，就是尾號是 1 的數據量，這是屬於ideal world沒有的額外信息，因此是需要保護的，一般的 PSI 解決這個問題是通過padding填充，例如Alice原來尾號是 1 的有兩個數據，現在把它填到四條，Bob也不知道Alice到底有多少條數據尾號是1。但是padding填充是會影響性能的。PETS上就有一篇工作是引入 DP 來添加padding，這樣整體的 PSI 性能就會提升。

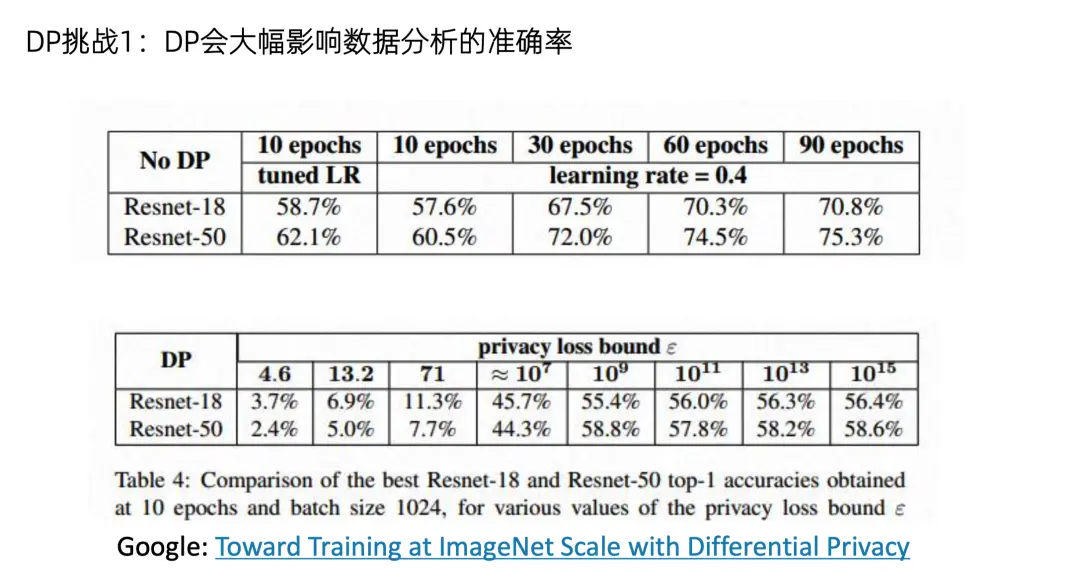
總而言之DP可以用於各種場景，和各種安全技術進行疊加。但是DP也存在一些挑戰，首先就是它會大幅影響數據分析的準確率。例如Google的一篇最新的文章，在imagenet上訓練一個神經網絡。沒有 DP 的話，準確率可以達到 60% 到 70%。但是開了 DP 之後，準確率就跌到3%~10%。所以在這種大規模數據建模場景中，如何使用差分隱私又不影響性能，是一個非常有挑戰的問題。

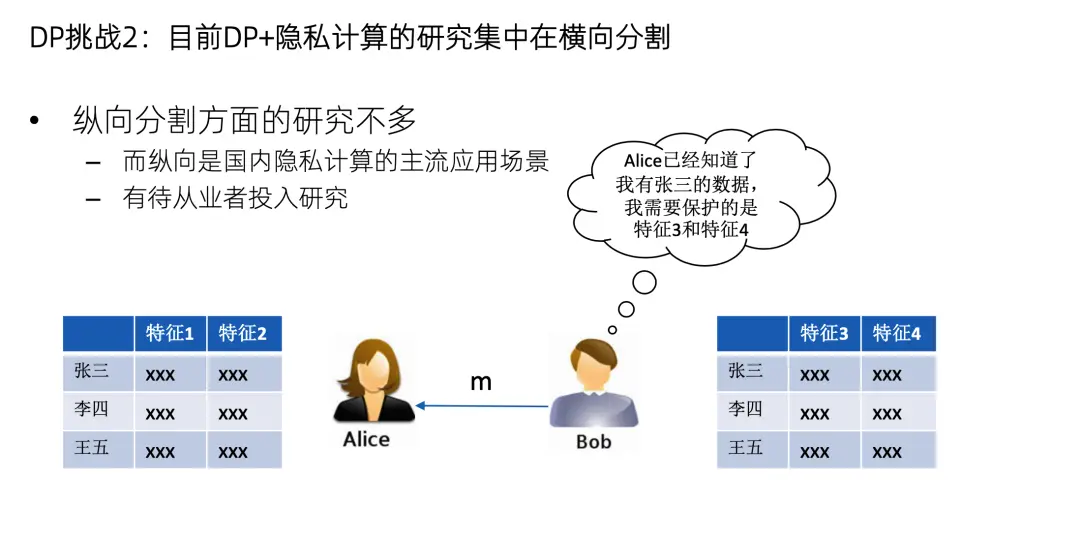
第二個挑戰是現在DP的研究成果主要是用在橫向分割，因為橫向分割和DP-SGD的結合是非常直觀的。但是DP在縱向分割方面的應用研究不多。縱向建模是已經把樣本對齊了的，也就是Alice 已經知道Bob有張三的數據了，現在保護的目標不是張三的數據在不在，而是張三的特徵是多少，這需要新的DP方法，但這方面的研究目前還不多。國內的主要應用場景都是縱向的，所以縱向怎麼加DP，有待從業者來投入精力去研究。

總結一下，本文分享了兩種可證明安全的方法。第一種是基於遊戲或者模擬的密碼學證明方式，其目標是刻畫信息的整體泄露邊界，證明在這個邊界之外的信息是絕對不泄露的。第二種是基於差分隱私的證明方式，目標是防止攻擊者重識別到單條數據，而不關注數據集整體泄露的信息量多少。這兩種都是已經得到了業界廣泛認可的安全證明方式。呼籲隱私計算業界能夠做好可證明安全，讓方案的安全性可以看得見摸得着。今天的分享就到這裏，謝謝大家。