博客 / 詳情

返回

K-D Tree 相關

部分發表於洛谷。

簡介：

K-D Tree 是一種適用於 \(k\) 維空間信息處理的數據結構，一般是維護 \(n\) 個點的信息，建出平衡二叉樹；在 \(k\) 比較小的

建樹：

一般使用交替建樹，遞歸的分為以下三個步驟：

  • 交替選擇一個維度切割（即 \(x, y, z, \cdots\) 依次切一遍，最後回到 \(x\) 繼續切）。

  • 選擇一個切割點將這個維度切割了。

  • 然後遞歸到被切割點切開的兩個超立方體繼續切割，直到區域內沒有點。

一個切割點的左右兒子是其切開的兩個超立方體的切割點。

為了維持二叉樹的平衡，要左右子樹儘量均勻，所以一般選擇這個切割維度的中位數作為切割點。

此時得到的樹高顯然是 \(\log n + O(1)\) 級別的。

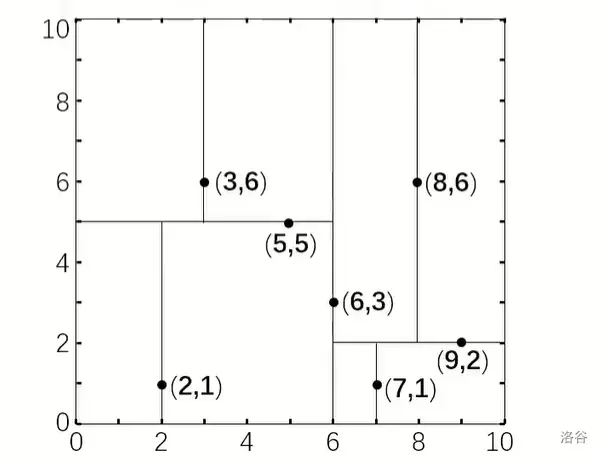
為了方便理解，給定一個在二維平面的例子：

選自 b 站董曉算法，若侵權聯繫可刪

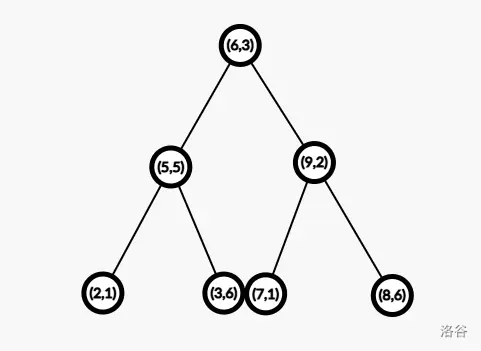
此時建出的 K-D Tree 就是：

可以使用 nth_element 輔助建樹，時間複雜度為 \(O(n \log n)\)。

為了方便操作，對於每個點，可以維護其被切割時的超立方體，即可以記錄其子樹內每個維度的最大最小值。

最近點對：

即對於每個點，求出到其它點的最短距離。

設查詢點是 \(a\)，依然是遞歸的形式的從 \(rt\) 進入（設當前到了 \(p\)）：

  • 先用 \(\operatorname{dis}(a, p)\) 更新答案 \(ans\)。

  • 然後求出 \(p\) 到左右子樹所代表的超立方體的最短距離 \(disl, disr\)，如果大於 \(ans\)，則直接剪枝。

  • 否則進入 \(disl, disr\) 更小的那個子樹先更新，出來時再判斷是否比另外一個更優；這是估價型剪枝。

提示： 使用 K-D Tree 單次查詢最壞是 \(O(N)\) 的，但是如果沒有特意卡的情況下，還是可以騙到很多分的。

操作：

對於一個高維矩形 \(Q\) 內的點的查詢，可以遞歸式的從 \(rt\) 開始判斷（設當前到了 \(p\)）：

  • 若包含 \(p\) 子樹，則直接返回所有點的信息。

  • 若與 \(p\) 子樹所在超立方體有交，先考慮 \(p\) 本身的貢獻，然後遞歸到左右子樹處理。

  • 否則無交，直接退出。

考慮時間複雜度分析，先考慮二維情況，根據遞歸，顯然時間複雜度是跟與 \(Q\) 相交的點（且沒有被 \(Q\) 包含）的數量，將這些點分為兩類：

  • 完全包含 \(Q\)：即樹上一條到根的鏈，點數是 \(O(h) = O(\log n)\) 的。

  • 部分與 \(Q\) 相交：顯然這些點所代表的矩形互不相交。

考慮求與 \(Q\) 相交的矩形的數量，顯然這些與 \(Q\) 相交的矩形必然至少與一條 \(Q\) 的邊相交；於是可以轉化為與一條邊相交的矩形的數量：

  • 考慮一個點 \(p\) 所代表的矩形，通過兩次切割將這個矩形分為了四個部分，每個部分為 \(p\) 的孫子來表示，而一條平行於座標軸的直線顯然最多穿越這個四個部分中的兩個部分。

這裏闡述了要交替維度切割建樹的原因，因為如果不交替切割，一條直線可能會直接穿過這四個部分。

因為子樹大小几乎是嚴格的一半，於是可以得到遞推式子：

\[T(n) = 2T(\frac{n}{4}) + O(1) \]

得到 \(T(n) = \sqrt n\)；拓展到 \(k\) 維上，類似的，是 \(T(n) = 2^{k - 1} T(\frac{n}{2^k}) + O(1)\)，於是 \(T(n) = O(n^{1 - \frac{1}{k}})\)（這裏是將 \(k\) 當做常數計算的，實際上常數要大不少）。

插入/刪除：

先説刪除，比較簡單，不需要真的將這個點刪除，就把這個點打上懶標記，將其貢獻清除即可，時間複雜度是 \(O(h) = O(\log n)\) 的；如果要真刪的話，也可以用下面的重構方法。

如果直接插入，就是遞歸式的，根據是否在左右子樹的超立方體內判斷插入到哪裏，最後到達空節點。

但是這樣可能會導致二叉樹不平衡，使得查詢複雜度出錯；然後大家可能會想到替罪羊樹的方法，定義一個平衡因子 \(\alpha\)，如果子樹大小超了，就子樹重構，可以保證樹高是 \(O(\log n)\) 的。

但是請注意，複雜度分析中，其四個孫子最多隻有兩個孫子被算進去，同時根據兒子子樹嚴格減半，可以得到遞推式；而替罪羊樹的方法，只保證了樹高是 \(O(\log n)\) 的，沒有保證子樹節點數量，所以若那條 \(Q\) 中的線恰好穿過四個孫子中兩個子樹最大的孫子，複雜度將會被卡滿出問題，具體複雜度不太清楚，但是應該能卡？

於是可以想到兩種著名的重構算法：

  • 根號重構。

  • 二進制分組。

根號重構，即我每插入 \(B\) 個點後再重構，存下插入的點，每次查詢是 \(O(B + n^{1 - \frac{1}{k}})\) 的；重構 \(\frac{n}{B}\) 次，複雜度是 \(O(\frac{n^2 \log n}{B})\)，均攤下來單次插入複雜度是 \(O(\frac{n \log n}{B})\)，取 \(B = \sqrt{n \log n}\) 最優；插入複雜度是 \(O(\sqrt{n \log n})\)，查詢 \(O(\sqrt{n \log n} + n^{1 - \frac{1}{k}})\)；常數一般，可以使用。

二進制分組，即將 \(n\) 二進制拆分，維護若干個二次冪大小的 K-D Tree；每次新加一個點，即新建一個大小 \(2^0\) 的 K-D Tree，然後不斷將相同大小的樹合併（實現時把所有需要合併的點，全部拿出來合併即可，而不是真的依次合併，這樣過於浪費）；因為合併帶 \(\log\)，所以最後均攤複雜度是 \(O(n \log^2 n)\) 的；查詢就是在每個樹上查一遍，最後累加起來，是一個等比數列累加的形式，也是 \(O(n^{1 - \frac{1}{k}})\) 的；常數很小。

例題：P4148 簡單題

題意：

二維平面上，單點加，區間矩形查；強制在線。

思路：

板子題，使用上面任意一種重構方式即可通過。

code

P14312 【模板】K-D Tree

題意：

\(k\) 維平面上，動態插入點，高維矩形內的點加，高維矩形內的點查。

思路：

重構使用二進制分組形式。

對於高維矩形內的點加，使用懶標記維護即可，注意懶標記的下傳等。

時間複雜度是 \(O(m \log^2 m + qm^{1 - \frac{1}{k}})\)。

完整代碼：

#include<bits/stdc++.h>
#define lowbit(x) x & (-x)
#define pi pair<ll, ll>
#define ls(k) k << 1
#define rs(k) k << 1 | 1
#define fi first
#define se second
using namespace std;
typedef __int128 __;
typedef long double lb;
typedef double db;
typedef unsigned long long ull;
typedef long long ll;
const int N = 1.5e5 + 10, M = 18, K = 3;
inline ll read(){
	ll x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9'){
		if(c == '-')
			f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9'){
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return x * f;
}
inline void write(ll x){
	if(x < 0){
		putchar('-');
		x = -x;
	}
	if(x > 9)
		write(x / 10);
	putchar(x % 10 + '0');
}
ll ans;
int n, m, op, w, rk, nowk, cnt;
int h[N], rt[M];
struct point{
	ll X[K];
	point(){
		memset(X, 0, sizeof(X));
	}
	inline bool operator<(const point&rhs)const{
		return X[nowk] < rhs.X[nowk];
	}
}a;
struct KD_Node{
	point a, mn, mx;
	int siz, lson, rson;
	ll data, sum, tag;
	inline bool operator<(const KD_Node&rhs)const{
		return a < rhs.a;
	}
}Q, T[N];
inline void getmin(ll &x, ll y){
	x = (x < y) ? x : y;
}
inline void getmax(ll &x, ll y){
	x = (x > y) ? x : y;
}
inline void pushup(int k){
	T[k].siz = T[T[k].lson].siz + 1 + T[T[k].rson].siz;
	T[k].sum = T[k].data + T[T[k].lson].sum + T[T[k].rson].sum;
	for(int i = 0; i < rk; ++i){
		T[k].mn.X[i] = T[k].mx.X[i] = T[k].a.X[i];
		if(T[k].lson){
			getmin(T[k].mn.X[i], T[T[k].lson].mn.X[i]);
			getmax(T[k].mx.X[i], T[T[k].lson].mx.X[i]);
		}
		if(T[k].rson){
			getmin(T[k].mn.X[i], T[T[k].rson].mn.X[i]);
			getmax(T[k].mx.X[i], T[T[k].rson].mx.X[i]);			
		}
	}
}
inline void add(int k, ll v){
	if(!k)
	  return ;
	T[k].data += v;
	T[k].tag += v;
	T[k].sum += v * T[k].siz;
}
inline void push_down(int k){
	if(T[k].tag){
		add(T[k].lson, T[k].tag);
		add(T[k].rson, T[k].tag);
		T[k].tag = 0;
	}
}
inline int build(int l, int r, int k){
	if(l > r)
	  return 0;
	nowk = k;
	int mid = (l + r) >> 1;
	nth_element(h + l, h + mid, h + r + 1, [](int x, int y) {return T[x] < T[y];});
	k = (k + 1) % rk;
	T[h[mid]].lson = build(l, mid - 1, k);
	T[h[mid]].rson = build(mid + 1, r, k);
	pushup(h[mid]);
	return h[mid];
}
inline void reset(int &k){
	if(!k)
	  return ;
	h[++cnt] = k;
	push_down(k);
	reset(T[k].lson);
	reset(T[k].rson);
	k = 0;
}
inline ll query(int k){
	if(!k)
	  return 0;
	bool flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].mn.X[i] && T[k].mx.X[i] <= Q.mx.X[i]);
	if(flag)
	  return T[k].sum;
	for(int i = 0; i < rk; ++i)
	  if(Q.mx.X[i] < T[k].mn.X[i] || T[k].mx.X[i] < Q.mn.X[i])
		return 0;
	flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].a.X[i] && T[k].a.X[i] <= Q.mx.X[i]);
	ll sum = 0;
	if(flag)
	  sum = T[k].data;
	push_down(k);
	sum += query(T[k].lson);
	sum += query(T[k].rson);
	return sum;
}
inline void upd(int k, ll v){
	if(!k)
	  return;
	bool flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].mn.X[i] && T[k].mx.X[i] <= Q.mx.X[i]);
	if(flag){
		add(k, v);
		return ;
	}
	for(int i = 0; i < rk; ++i)
	  if(Q.mx.X[i] < T[k].mn.X[i] || T[k].mx.X[i] < Q.mn.X[i])
		return ;
	flag = 1;
	for(int i = 0; i < rk; ++i)
	  flag &= (Q.mn.X[i] <= T[k].a.X[i] && T[k].a.X[i] <= Q.mx.X[i]);
	if(flag)
	  T[k].data += v;
	push_down(k);
	upd(T[k].lson, v);
	upd(T[k].rson, v);
	pushup(k);
}
int main(){
//	freopen("A.in", "r", stdin);
	rk = read(), m = read();
	while(m--){
		op = read();
		if(op == 1){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			w = read() ^ ans;
			T[++n] = {a, a, a, 0, 0, 0, w, w, 0};
			cnt = 0;
			h[++cnt] = n;
			for(int i = 0; i < M; ++i){
				if(!rt[i]){
					rt[i] = build(1, cnt, 0);
					break;
				}
				else
				  reset(rt[i]);
			}
		}
		else if(op == 2){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			Q.mn = a;
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;	
			Q.mx = a;
			w = read() ^ ans;
			for(int i = 0; i < M; ++i)
			  if(rt[i])
				upd(rt[i], w);
		}
		else if(op == 3){
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;
			Q.mn = a;
			for(int i = 0; i < rk; ++i)
			  a.X[i] = read() ^ ans;	
			Q.mx = a;
			ans = 0;
			for(int i = 0; i < M; ++i)
			  if(rt[i])
				ans += query(rt[i]);
			write(ans);
			putchar('\n');
		}
		else
		  break;
	}
	return 0;
}
後端
user avatar
0 位用戶收藏了這個故事！

發佈 評論

Some HTML is okay.