博客 / 詳情

返回

Morris遍歷(線索二叉樹)

前言

現將左老師課上的morris遍歷內容進行歸納整理，java版本代碼均為左老師課上代碼，c++代碼為本人直接改寫，並均通過leetcode測試。

什麼是morris遍歷

morris遍歷是利用二叉樹本身空閒出來的指針(n個節點的二叉樹有n+1個指針空閒)來作為輔助變量完成二叉樹的遍歷的一種方法。Morris遍歷法能以O(1)的空間複雜度和O(n)的時間複雜度實現二叉樹的三種遍歷,其中不使用棧或額外空間。

morris遍歷流程

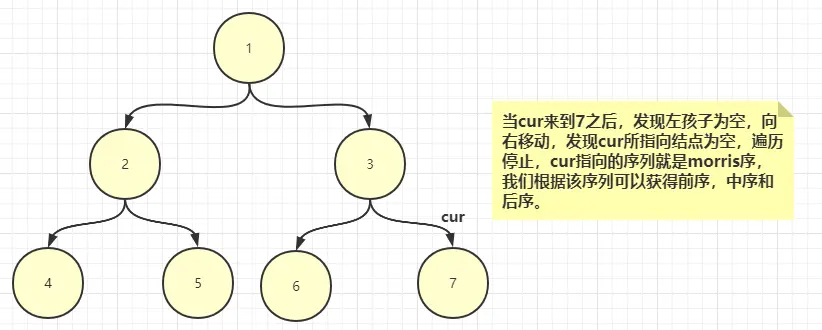
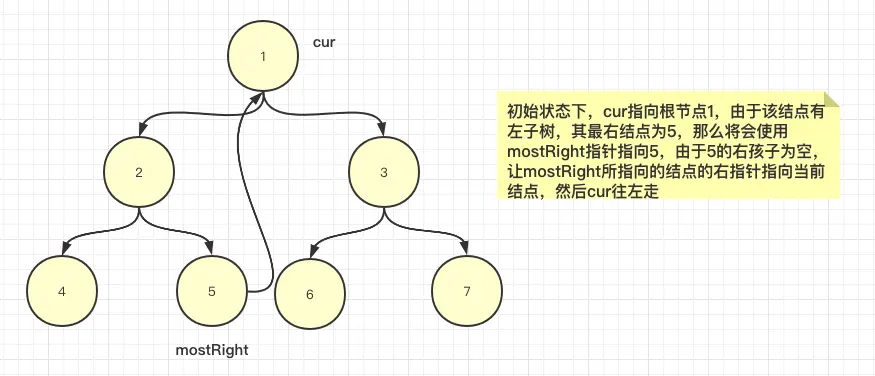
1、我們使用cur指針指向當前結點，mostRight指針指向cur左子樹的最右結點，也即是cur的前驅結點
2、如果當前結點沒有左子樹，我們讓cur往右走
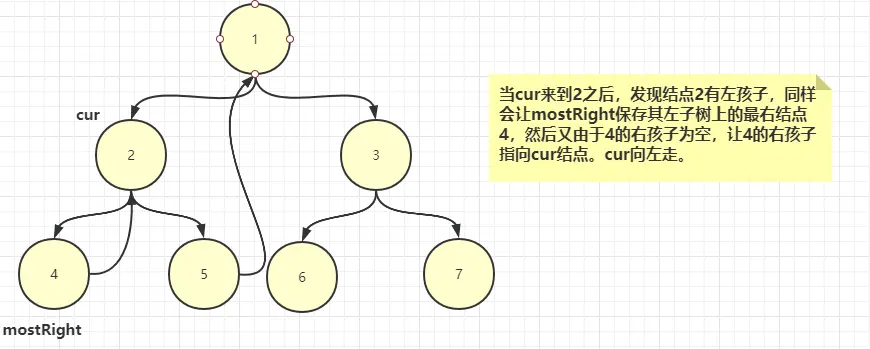
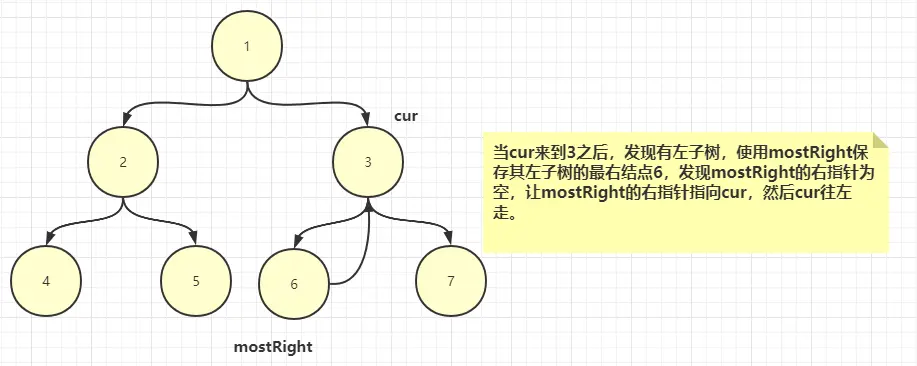
3、如果有左子樹，那麼找到其左子樹的最右結點(原樹中的最右結點，而不是修改過指針的最右結點，看到後面就清楚了)，並使用mostRight保存。
    3.1、如果mostRight的右指針為空，(説明此時是第一次來到cur所指向結點)，讓mostRight的右指針指向cur，然後讓cur往左走。
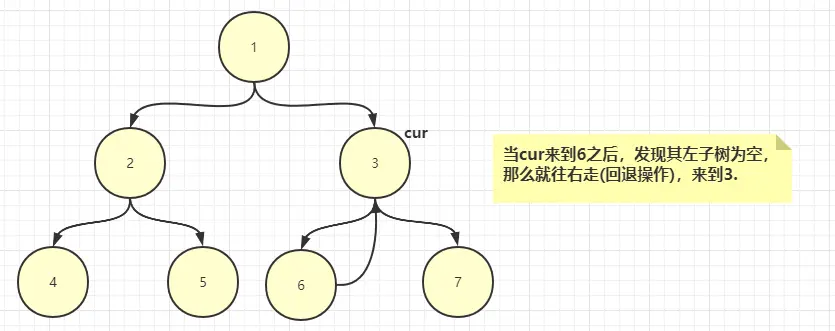
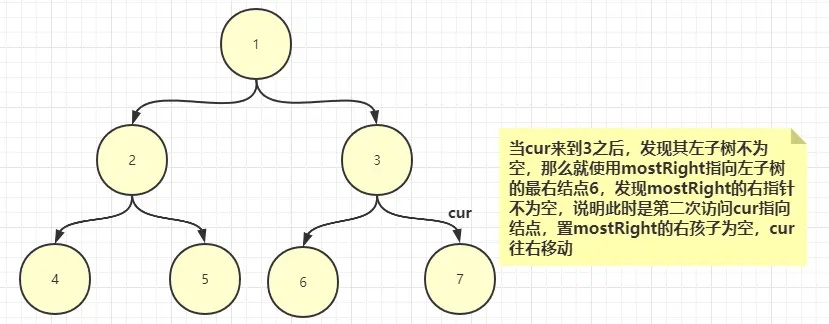
    3.2、如果mostRight的右指針不為空，(説明此時是第二次來到cur所指向結點)，讓mostRight的右指針重新置為null，然後cur往右走
4、如果當前結點為空，遍歷停止(回退過程合併到往右走了)。
morris遍歷圖解：

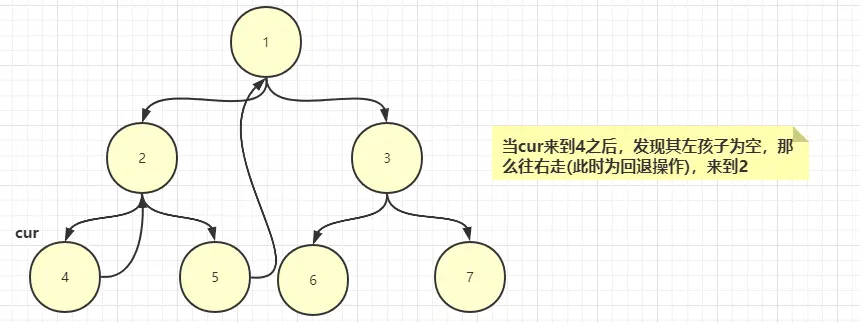
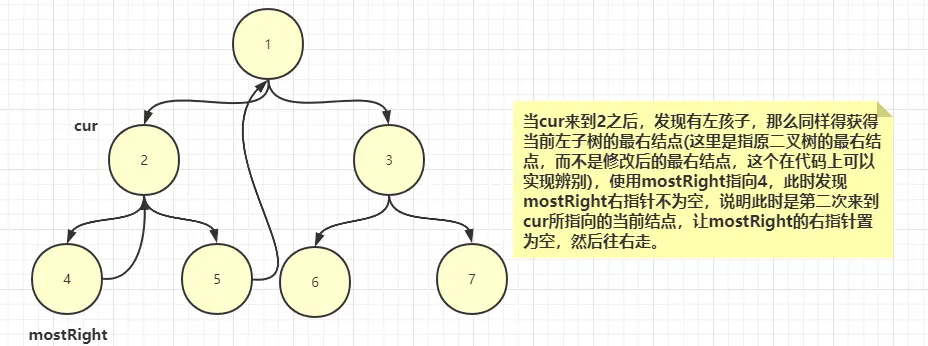
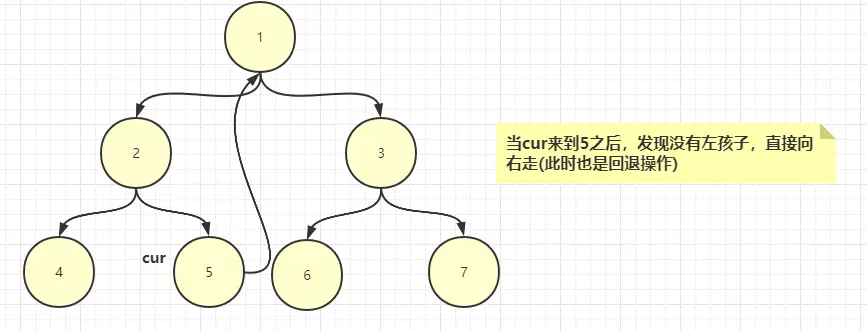
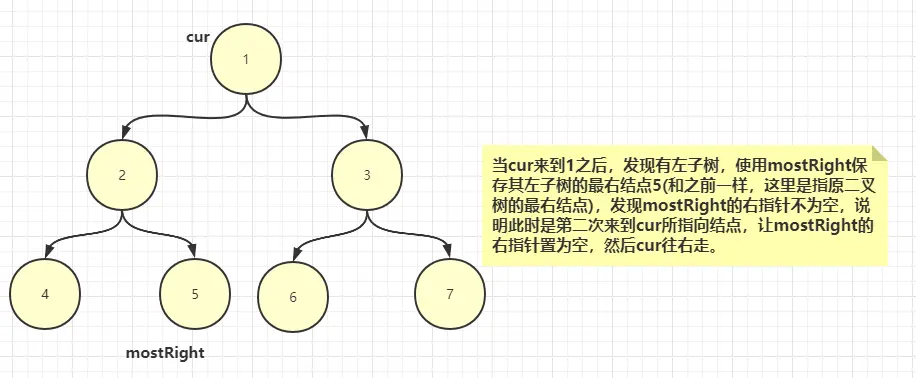
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png

morris序

在進行morris遍歷的時候每次遍歷都訪問該節點所獲得的訪問順序就是morris序。在上述例子中的morris如下

1 2 4 2 5 1 3 6 3 7

可以看到有的節點訪問了兩次有的節點只訪問了一次，根據這個特點我們可以推導出morris的前序，中序和後序序列，並且這裏得記住一個特點就是，只有有左孩子的節點才會被訪問兩次，沒有左孩子的只會訪問一次。

morris序的代碼實現

java版本
public static class Node {
   public int value;
   Node left;
   Node right;

   public Node(int data) {
       this.value = data;
   } 
}

public static void morris(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) { // 有左樹的情況下
            // 找到cur左樹上，真實的最右
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            // 從while中出來，mostRight一定是cur左樹上的最右節點
            // mostRight
            if (mostRight.right == null) {// 第一次來到cur結點
                mostRight.right = cur;
                cur = cur.left;
                continue;
            } else { // mostRight.right != null -> mostRight.right == cur
                mostRight.right = null;
            }
        }
        // 沒有左子樹或者第二次來到cur結點
        cur = cur.right;
    }
}
c++版本
struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  };
void morris(TreeNode* root){
    if(!root) return;
    TreeNode* cur=root;
    TreeNode* mostRight;
    while(cur){
        mostRight = cur->left;
        if(mostRight){
            // 有左子樹
            while(mostRight->right&&mostRight->right!=cur){
                // 只要有右孩子並且右孩子不是當前結點
                mostRight = mostRight->right;
            }
            if(!mostRight->right){
                // mostRight的右孩子為空，説明是第一次訪問cur
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }else{
                // mostRight的右孩子為cur，説明是第二次來到cur
                mostRight->right = nullptr;
            }
        }
        // 沒有左子樹或者第二次來到cur結點
        cur = cur->right;
    }
}

morris先序遍歷

先序遍歷就是在morris遍歷的時候在第一次遍歷當前結點的時候進行輸出即可，這裏直接給出代碼，會發現改動的地方就2處

java版本
public static void morrisPre(Node head) {
    if (head == null) {
        return;
    }
    Node cur1 = head;
    Node cur2 = null;
    while (cur1 != null) {
        cur2 = cur1.left;
        if (cur2 != null) {
            while (cur2.right != null && cur2.right != cur1) {
                cur2 = cur2.right;
            }
            if (cur2.right == null) {
                cur2.right = cur1;
                System.out.print(cur1.value + " ");
                cur1 = cur1.left;
                continue;
            } else {
                cur2.right = null;
            }
        } else {
            System.out.print(cur1.value + " ");
        }
        cur1 = cur1.right;
    }
    System.out.println();
}
c++版本
vector<int> result;// 保存先序遍歷
void morris(TreeNode* root){
    if(!root) return;
    TreeNode* cur=root;
    TreeNode* mostRight;
    while(cur){
        mostRight = cur->left;
        if(mostRight){
            // 有左子樹
            while(mostRight->right&&mostRight->right!=cur){
                // 只要有右孩子並且右孩子不是當前結點
                mostRight = mostRight->right;
            }
            if(!mostRight->right){
                // mostRight的右孩子為空，説明是第一次訪問cur
                result.push_back(cur->val);
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }else{
                // mostRight的右孩子為cur，説明是第二次來到cur
                mostRight->right = nullptr;
            }
        }else{
            // 沒有左子樹，只會遍歷一次，直接訪問
            result.push_back(cur->val);
        }
        // 沒有左子樹或者第二次來到cur結點
        cur = cur->right;
    }
}

morris中序遍歷

中序遍歷就是在morris遍歷的時候在第二次遍歷當前結點的時候進行輸出即可，這裏同樣直接給出代碼，需要修改的地方就一處。

java版本
public static void morrisIn(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) {
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            if (mostRight.right == null) {
                mostRight.right = cur;
                cur = cur.left;
                continue;
            } else {
                mostRight.right = null;
            }
        }
        System.out.print(cur.value + " ");
        cur = cur.right;
    }
    System.out.println();
}
c++版本
vector<int> result;// 保存中序遍歷結果
void morris(TreeNode* root){
    if(!root) return;
    TreeNode* cur=root;
    TreeNode* mostRight;
    while(cur){
        mostRight = cur->left;
        if(mostRight){
            // 有左子樹
            while(mostRight->right&&mostRight->right!=cur){
                // 只要有右孩子並且右孩子不是當前結點
                mostRight = mostRight->right;
            }
            if(!mostRight->right){
                // mostRight的右孩子為空，説明是第一次訪問cur
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }else{
                // mostRight的右孩子為cur，説明是第二次來到cur
                mostRight->right = nullptr;
            }
        }
        // 沒有左子樹或者第二次來到cur結點
        result.push_back(cur->val);
        cur = cur->right;
    }
}

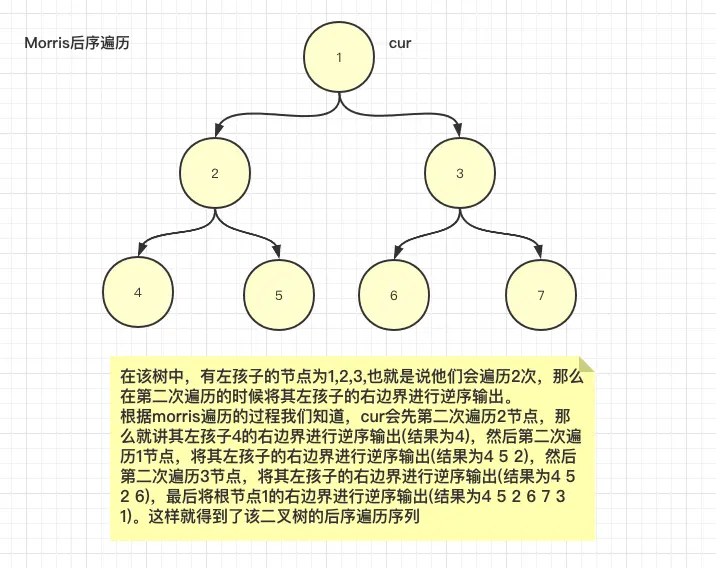
morris後序遍歷

後序遍歷的處理有點複雜，因為沒有哪個節點是遍歷3次的，但是一樣可以利用遍歷2次的節點來處理，我們使用的方法時在第二次來到當前節點時，將該節點的左子樹的右邊界進行逆序輸出，直到左右有左子樹的節點的左子樹右邊界均輸出完畢，最後再把根節點的右邊邊界進行逆序輸出即可。説起來感覺有點抽象，看下面的例子就好。
image.png

那麼現在就只剩下一個問題了，morris遍歷是一個時間複雜度為O(n),空間複雜度為O(1)的算法，如何原地逆置任意節點的左子樹的右邊界呢？
答案是單鏈表逆置，我們在每一次需要逆序輸出右邊界的時候就使用單鏈表逆置的方法將右邊界節點逆置，然後再從尾往前輸出就好，輸出完畢後再逆置還原。
java版本
public static void morrisPos(Node head) {
    if (head == null) {
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null) {
        mostRight = cur.left;
        if (mostRight != null) {
            while (mostRight.right != null && mostRight.right != cur) {
                mostRight = mostRight.right;
            }
            if (mostRight.right == null) {
                mostRight.right = cur;
                cur = cur.left;
                continue;
            } else {
                mostRight.right = null;
                printEdge(cur.left);
            }
        }
        cur = cur.right;
    }
    printEdge(head);
    System.out.println();
}
public static void printEdge(Node head) {
    Node tail = reverseEdge(head);
    Node cur = tail;
    while (cur != null) {
        System.out.print(cur.value + " ");
        cur = cur.right;
    }
    reverseEdge(tail);
}
public static Node reverseEdge(Node from) {
    Node pre = null;
    Node next = null;
    while (from != null) {
        next = from.right;
        from.right = pre;
        pre = from;
        from = next;
    }
    return pre;
}
c++版本
struct TreeNode {
  int val;
  TreeNode *left;
  TreeNode *right;
  TreeNode() : val(0), left(nullptr), right(nullptr) {}
  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

vector<int> result;

TreeNode* reverseEdge(TreeNode* root){
    TreeNode* pre = nullptr;
    TreeNode* next = nullptr;
    while(root){
        next = root->right;
        root->right = pre;
        pre = root;
        root = next;
    }
    return pre;
}
void printRightEdge(TreeNode* root){
    TreeNode* tail = reverseEdge(root);// 獲得逆置後的尾結點
    TreeNode* cur = tail;//暫存尾結點作為工作節點，最後得重新逆置tail還原
    while(cur){
        result.push_back(cur->val);
        cur = cur->right;
    }
    reverseEdge(tail);
}
void morris(TreeNode* root){
    if(!root) return;
    TreeNode* cur = root;
    TreeNode* mostRight = nullptr;
    while(cur){
        mostRight = cur->left;
        if(mostRight){
            while(mostRight->right&&mostRight->right!=cur){
                mostRight = mostRight->right;
            }
            if(!mostRight->right){
                // 第一次遍歷cur節點
                mostRight->right = cur;
                cur = cur->left;
                continue;
            }else{
                mostRight->right = nullptr;
                printRightEdge(cur->left);
            }
        }
        // 沒有左孩子或者第二次遍歷到cur節點
        cur = cur->right;
    }
    // 最後處理根節點的右邊界
    printRightEdge(root);
}
遍歷 , 二叉樹 , 數據結構和算法
user avatar
0 位用戶收藏了這個故事！

發佈 評論

Some HTML is okay.