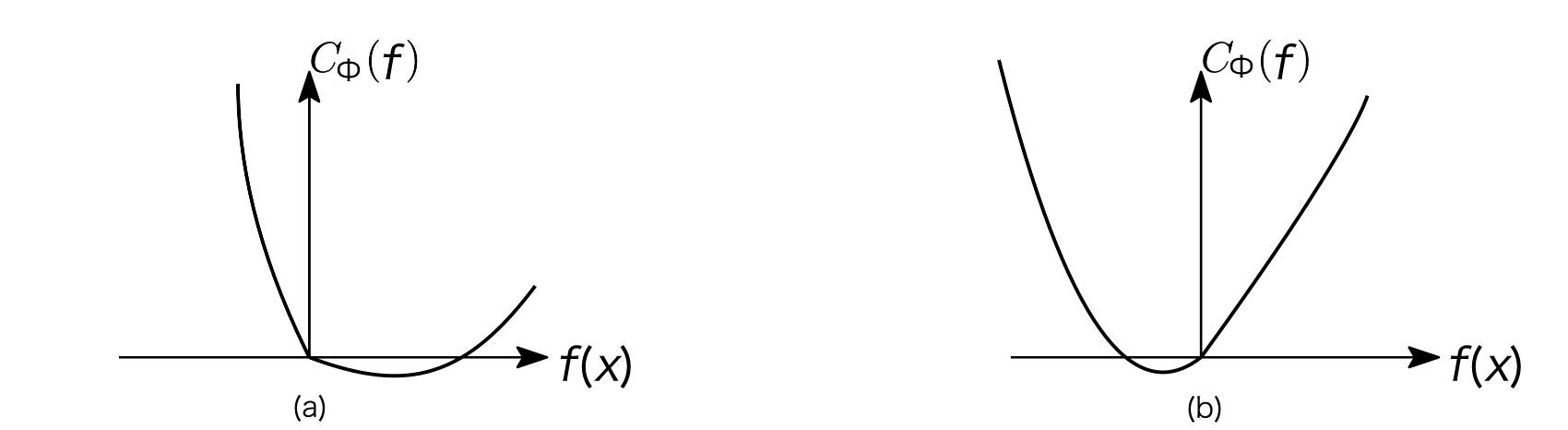這學期參加了同研究科的田中研的讀書會，所選的是近年出的較新的書《Learning Theory from First Principles》^[1]：

作者Francis Bach是COLT2025的keynote speaker^[2]。我承擔了4.1-4.4部分（這周做了分享），該部分和我目前的科研方向比較相關。下面是我結合自己的科研的一些心得和筆記。

1 導引

給定\(\mathcal{X}\times\mathcal{Y}\)上的聯合概率分佈\(p(x, y)\)，以及損失函數\(L:\mathcal{Y}\times \mathcal{Y}\rightarrow \mathbb{R}\)，定義預測函數\(h:\mathcal{X}\rightarrow \mathcal{Y}\)的期望風險（expected risk）（也稱泛化誤差（generalization error）或測試誤差（testing error））：

對於貝葉斯線性迴歸這類輸出的是一個預測分佈\(\hat{p}(t\mid x)\)的任務，其預測函數\(h(x)\)可以由條件期望\(h(x) = \mathbb{E}_t[t\mid x] = \int t\mathrm{d}\hat{p}\)表示，於是其期望風險可以寫為

注 當從數據中進行學習時，\(h\)依賴於隨機訓練數據而非測試數據，因此儘管\(R(h)\)的表達式中關於測試數據取了期望，但在通常情況下它仍然是隨機的。然而，\(R(h)\)做為關於\(h\)的泛函是確定性的。

接下來考慮學習問題，給定從概率分佈\(p(x, y)\)中i.i.d.採樣的大小為\(n\)的隨機樣本，目標為學習一個預測函數\(h:\mathcal{X}\rightarrow \mathcal{Y}\)使得期望風險\(R(h)\)最小化，或等價地，使得下列超額風險（excess risk）（或稱超額誤差（excess error））最小：

其中\(\inf_{h \space \text{measurable}}\)中的\(h\)為可測函數。在這篇博客中我們關注基於經驗風險最小化方法的統計分析。

然而，以二分類問題為例，預測函數\(h\)是個布爾函數，在其假設空間中的經驗風險最小化是難以處理的（intractable）組合優化問題。此外，分析這種布爾函數假設空間的複雜度可能需要進一步引入諸如VC維的工具。然而，可以通過凸代理損失的框架來學習一個實值函數\(f\)以將該問題凸化從而克服之。此時，我們就可以使用拉德馬赫複雜度來對經驗風險最小化的漸進收斂進行分析。

考慮二分類場景，做為直接學習\(h: \mathcal{X}\rightarrow \left\{-1, +1\right\}\)的替代，我們採用學習實值函數\(f: \mathcal{X}\rightarrow\mathbb{R}\)（其對應的函數族為\(\mathcal{F}\)）的方法，並定義\(h(x) = \mathrm{sign}(f(x))\)，其中

我們將關於函數\(h = \text{sign}\circ f\)的的0-1風險直接記為\(R_{\text{0-1}}(f)\)，它可以表示為：

注意，這裏出於簡潔，未嚴格討論\(f(x)=0\)的情形。記\(\mathbb{I}\left(yf(x)\leqslant 0\right):= \Phi_{\text{0-1}}\left(yf(x)\right)\)，其中\(\Phi_{\text{0-1}}\left(\cdot\right)\)稱為“基於間隔的”0-1損失函數（注意與滿足定義\(L_{\text{0-1}}(h(x), y) = \mathbb{I}\left(h(x)\neq y\right)\)的0-1損失函數\(L_{\text{0-1}}(\cdot, \cdot)\)相區分）。

2 凸代理

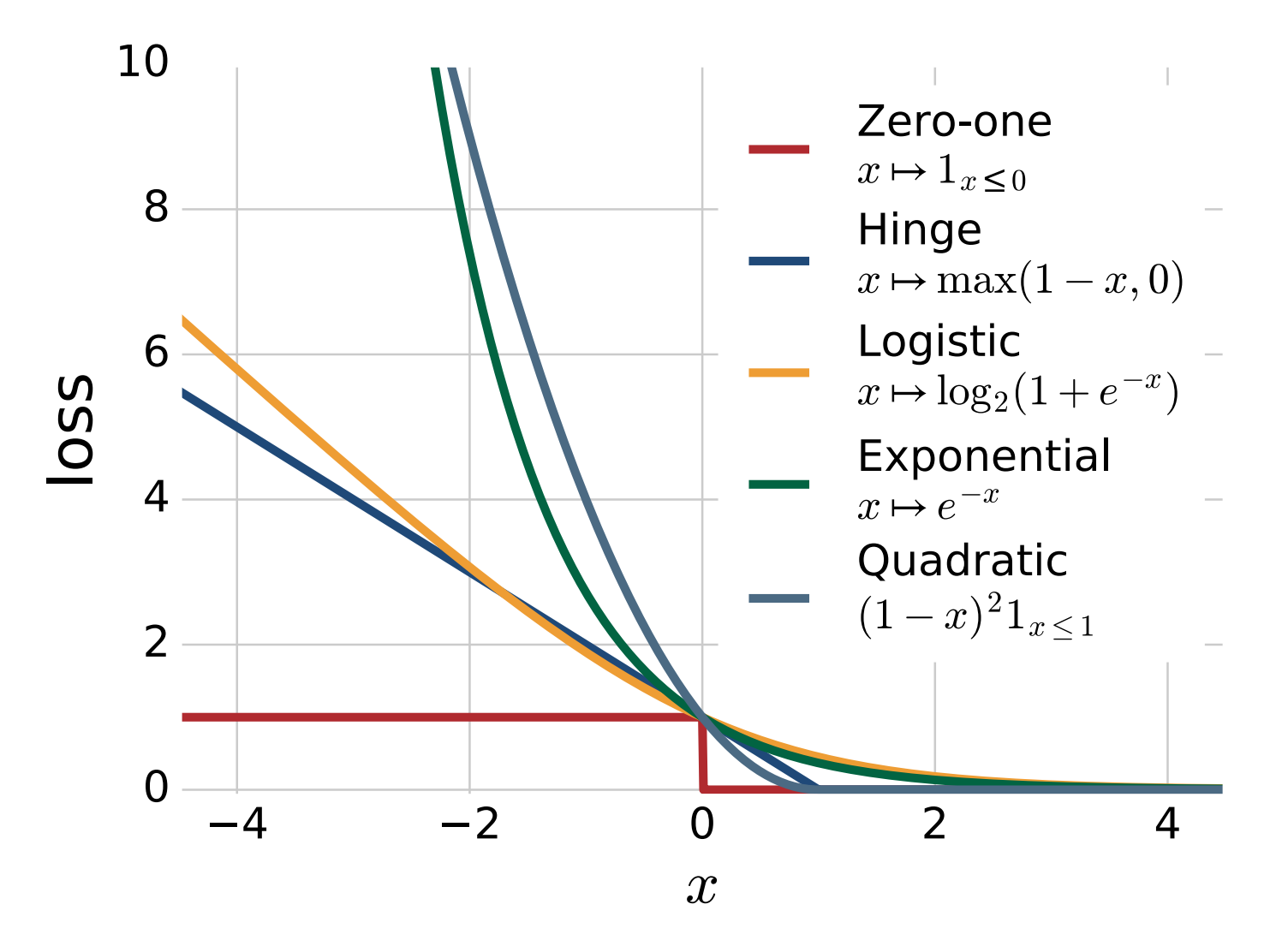
優化上述\(R(f)\)的經驗版本\(\frac{1}{m}\sum_{i=1}^m\mathbb{I}\left(y_if(x_i)\leqslant 0\right)\)是NP-hard的（由於\(\mathbb{I}\left(yf(x)\leqslant 0\right)\)非凸不連續），因此我們可以考慮使用凸代理(convex surrogates) 技術對目標函數\(\Phi_{\text{0-1}} = \mathbb{I}\left(yf(x)\leqslant 0\right)\)進行凸放鬆，其中我們使用具有更好的數值屬性的函數\(\Phi\)（主要是凸性）對\(\Phi_{\text{0-1}}\)進行替代。下面是一些凸代理損失函數的例子^[3]：

注 深度學習中的sigmoid函數\(\Phi(t) = 1 / (1 + e^{-t})\)也可以看做一種針對\(\frac{1}{2}\mathbb{I}(t\geqslant 0)\)的光滑連續的非凸替代函數^[5]。

於是，做為對直接優化0-1風險\(R_{\text{0-1}}(f)\)（或其經驗版本）的替代，我們轉而優化下列的代理風險\(R_{\Phi}(f)\)（及其經驗版本）：

3 校準與條件風險

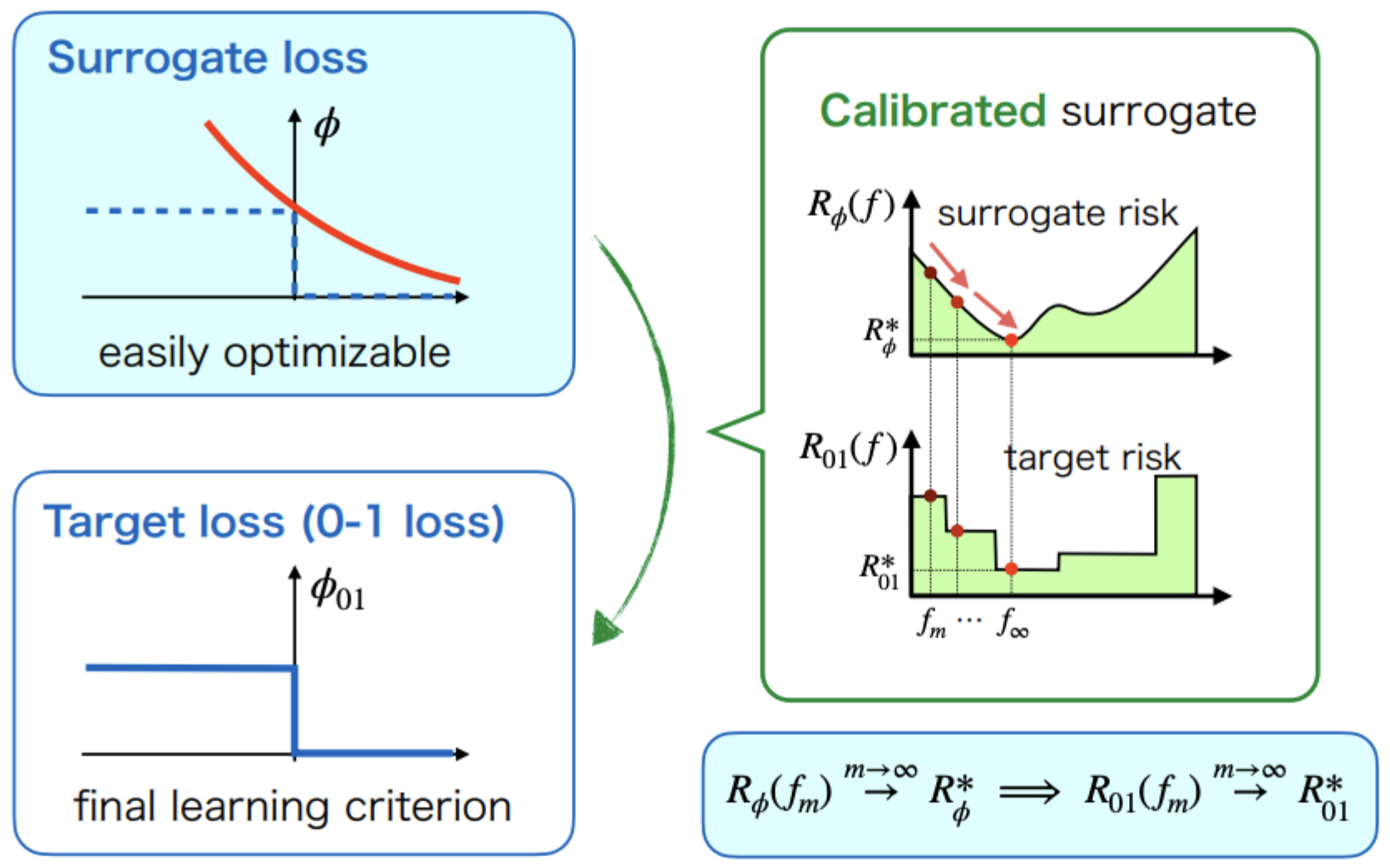
理想的代理損失函數\(\Phi\)應該滿足代理風險一致性(Surrogate risk consistency)^[4][5]：在總體層面上對\(\Phi\)-風險的優化能夠確保優化對0-1風險的優化：

代理風險一致性 (Surrogate risk consistency) 若對優化代理經驗風險得到的任意函數序列\(\hat{f}_1, \hat{f}_2, \cdots, \hat{f}_m, \cdots\)，以及任意分佈\(p(x, y)\)滿足：

則稱損失\(\Phi\)對原目標損失\(\mathcal{\Phi}_{\text{0-1}}\)是代理風險一致的，或Bayes一致的/Fisher一致的，有時也稱代理損失函數\(\Phi\)是校準 （calibrated） 的。直觀地理解可以參見下圖^[6]：

直觀理解地，代理風險一致性也就意味着能夠最小化\(R_{\Phi}(f)\)的輸出函數也能夠最小化\(R_{\text{0-1}}(f)\)。那麼我們接下來先來考慮最小化\(R_{\text{0-1}}(f)\)的問題。

為了進一步簡化後續的分析，我們根據條件期望以及其相關的全期望定理，將\(R_{\text{0-1}}(f)\)寫為：

其中\(\eta(x) = p(y=+1\mid x)\)，我們有\(\mathbb{E}[y\mid x] = 2\eta(x) - 1\)。我們稱其中內層的條件期望項為0-1間隔損失\(\Phi_{\text{0-1}}\)的條件風險（conditional risk）（也稱為pointwise風險^[2]），由於在其計算過程中\(y\)取期望取掉了，因此該項只和\(f(x)\)相關，因此我們將其記為\(C_{\text{0-1}}(f)\)：

我們用\(C^*_{\text{0-1}} = \inf_{f} C_{\text{0-1}}(f)\)來表示最優的\(\Phi_{\text{0-1}}\)的條件風險，可得

而最優\(0-1\)風險（也稱貝葉斯風險（Bayes risk））可以表示為：

上式也可進一步寫為$ R_{\text{0-1}}^* = \mathbb{E}_{x}\left[\frac{1}{2} - \frac{1}{2}\left|\mathbb{E}[y\mid x]\right|\right]$。

此時最優實值函數（也稱貝葉斯實值函數（Bayes real-valued function））\(f^*_{\text{0-1}}\)需要滿足當\(\eta(x) < \frac{1}{2}\)時，\(f^*_{\text{0-1}}(x) < 0\)，當\(\eta(x) > \frac{1}{2}\)時，\(f^*_{\text{0-1}}(x) > 0\)，當\(\eta(x)=\frac{1}{2}\)時，\(f^*_{\text{0-1}}(x)\)可以是任意實數。於是，\(f^*_{\text{0-1}}\)滿足：

我們稱滿足\(h^* = \mathrm{sign}(2\eta - 1)\)（\(=\mathrm{sign}\left(\mathbb{E}[y|x]\right)\)）的分類器為貝葉斯最優分類器，或直接簡稱為貝葉斯分類器（Bayes's classifier）。這裏可以與在線性迴歸問題中得到的最優預測器\(h^* = \mathbb{E}[y|x]\)進行對照。

我們用\(C_{\Phi}\)來表示代理損失\(\Phi\)的條件風險，並用\(C^*_{\Phi}\)來表示其對應的最優條件風險，用\(R^*_{\Phi}\)來表示其對應的最優期望風險。

由上述內容可知，對於代理損失\(\Phi\)而言，如果也能確保其對應的最優實值輸出函數\(f_{\Phi}^*\)在\(\eta(x) \neq \frac{1}{2}\)時與\(2\eta(x) - 1\)同號，那麼它就是校準的。

可以證明，當\(\Phi\)為凸函數時，存在一個可用的校準充要條件，如下述命題所示：

命題 ^[8] 設\(\Phi: \mathbb{R}\rightarrow \mathbb{R}\) 為凸函數。代理函數\(\Phi\)是校準的當且僅當\(\Phi\)在\(0\)處可微且\(\Phi^{\prime}(0) < 0\)。

證明 由於\(\Phi\)是凸的，則\(C_{\Phi}\)也是凸的，因此可以考慮\(\eta(x)\neq \frac{1}{2}\)時, \(C_{\Phi}(f)\)在0處的左和右導數以對關於最小值的位置進行分類討論，有如下所示的\((a)\)和\((b)\)兩種可能（最優點$ f^(x)> 0\(當且僅當在0點的右導數嚴格為負， 最優點\) f^(x) < 0$當且僅當在0點的左導數嚴格為正）：

(a) \(f^*_{\Phi}(x) > 0 \Leftrightarrow C_{\Phi}^{\prime}(0_{+}) = \eta(x)\Phi^{\prime}\left(0_{+}\right) - (1 - \eta(x))\Phi^{\prime}\left(0_{-}\right) < 0\)
(b) \(f^*_{\Phi}(x) < 0 \Leftrightarrow C_{\Phi}^{\prime}(0_{-}) = \eta(x)\Phi^{\prime}\left(0_{-}\right) - (1 - \eta(x))\Phi^{\prime}\left(0_{+}\right) > 0\)

先證明充分性。假設\(\Phi\)是校正的。如令上述等式\((a)\)中的\(\eta\rightarrow {\frac{1}{2}}_{+}\)，這將導致\(C_{\Phi}^{\prime}(0_{+}) = \frac{1}{2} \left[\Phi^{\prime}\left(0_{+}\right) - \Phi^{\prime}\left(0_{-}\right)\right]\leqslant 0\)。由於\(\Phi\)是凸的，等式\(\Phi^{\prime}\left(0_{+}\right) - \Phi^{\prime}\left(0_{-}\right)\geqslant 0\)恆成立。因此，\(\Phi^{\prime}\left(0_{+}\right) = \Phi^{\prime}\left(0_{-}\right)\)，這意味着\(\Phi\)在\(0\)處是可微的。由\((a), (b)\)與之前提到的同號條件可得，\(\Phi^{\prime}(0) < 0\)。

再證明必要性。假設\(\Phi\)在0點是可微的且\(\Phi^{\prime}(0) < 0\)，則\(C_{\Phi}^{\prime}(0) = (2\eta - 1)\Phi^{\prime}(0)\)，則由\((a), (b)\)可得之前提到的同號條件。於是原命題得證。

注意上述命題排除了凸代理\(\Phi(f) = (1-f)+ = \max\left\{1-f, 0\right\}\)，該函數在0點處不可微。此外，之前我們在第2部分提到的所有代理損失函數的例子都是校準的。

注 在使用概率模型進行分類的情況下，若學習\(p(y=1\mid x)\)的模型，則校準也可能指關於這個概率的估計的準確度。

4 代理損失函數的超額風險界

由前文敍述可知，任意\(x\in \mathcal{X}\)，若代理損失函數\(\Phi\)是校準的，則最小化條件代理風險\(C_{\Phi}(f)\)可以得到最優預測函數\(h^* = \text{sign}(f^*)\)。這個結果是當樣本數量\(m\rightarrow \infty\)時的漸近（asymptotic）結果。

接下來，我們要更進一步，得到一個非漸進（non-asymptotic）的結果：如果能夠控制代理超額風險（可以通過經驗風險最小化達到），就能夠控制目標超額風險。形式化地説，我們需要證明如下所示的代理損失函數的超額風險界：

對\(\forall f(x)\in \mathbb{R}\)成立，其中\(\Gamma: \mathbb{R}_{+}\rightarrow \mathbb{R}_{+}\)為滿足屬性\(\lim_{t\rightarrow 0^{+}}\Gamma (t) = 0\)的非遞減函數。

函數\(\Gamma(t)\)有時被稱為校準函數（calibration function） 或 超額風險率（excess risk rate）。這裏我們關注當\(t\rightarrow 0^{+}\)時，函數\(\Gamma(t)\)的表現。後面我們會證明hinge損失的校準函數是\(\mathcal{O}(t)\)的，而諸如平方和logistic損失的光滑凸代理則可能會導致\(\mathcal{O}(\sqrt{t})\)的校準函數。

注 由於這裏我們關注的是\(t\rightarrow 0^{+}\)時的情況，所以\(\mathcal{O}(t)\)是比\(\mathcal{O}(\sqrt{t})\)更緊的結果。因此，儘管hinge損失在光滑的性質上沒平方和logistic損失那麼好，但它所導出的校準函數結果更好，這也是一種“權衡”的體現。

現在我們考慮將期望風險轉換為我們之前提到的條件風險以簡化分析。由條件風險的定義可得，對\(\forall f(x)\in \mathbb{R}\)，有

若函數\(\Gamma\)是凹函數，則可利用Jensen不等式得到

於是，若能證明\(C_{\text{0-1}}(f) - C_{\text{0-1}}^*\leqslant \Gamma(C_{\Phi}(f) - C_{\Phi}^*)\)對\(\forall f(x)\in \mathbb{R}\)成立，則代理損失函數的超額風險界得證。

超額條件0-1風險的表達式

接下來我們考慮對\(C_{\text{0-1}}(f) - C_{\text{0-1}}^*\)進行表示。由前面提到的知識可知：

接下來我們需要對\(\eta(x)\)和\(f(x)\)的取值情況進行分類討論：

1. \(\eta(x) = \frac{1}{2}\):

   \(C_{\text{0-1}}(f) = \eta\Phi_{\text{0-1}}\left(f\right) + (1 - \eta)\Phi_{\text{0-1}}\left(-f\right) = \frac{1}{2}\)為常值函數，故\(C_{\text{0-1}}(f) - C_{\text{0-1}}^* = 0\)。

2. \(\eta(x) > \frac{1}{2}\):

   此時\(C^*_{\text{0-1}} = 1 - \eta\)（在$ f(x) > 0$時取得）。

   a. 當\(f(x) \leqslant 0\)時，\(C_{\text{0-1}}(f) - C_{\text{0-1}}^* = 2\eta - 1\)；
   b. 當\(f(x) > 0\)時，\(C_{\text{0-1}}(f) - C_{\text{0-1}}^* = 0\)。
   於是可以得到

3. \(\eta < \frac{1}{2}\):

   同理可得\(C_{\text{0-1}}(f) - C_{\text{0-1}}^* = \left(1 - 2\eta(x)\right)\Phi_{\text{0-1}}(-f(x))\)。

綜上所述，對任意\(\eta(x)\in [0, 1]\)：

我們也可以對其進行放鬆，以得到一個更加實用的結果：

其中\(b(f)\)為不改變\(f(x)\)符號的保號函數。

平方代理損失 對平方代理損失\(\Phi(f) = (f - 1)^2\)，我們有

\(C_{\Phi}^{\prime}(f) = 0\)當且僅當\(f^{*}_{\Phi} = 2\eta - 1\)時滿足，此時有\(C_{\Phi}^* = 4\eta(1 - \eta)\)，故

於是就能得到\(\Gamma(t) = \mathcal{O}(\sqrt{t})\)的平方代理損失的超額風險界；

我們接下來會擴展到更一般的光滑代理的校準結果。

光滑代理損失 我們考慮形式為\(\Phi(f) = F(f) - f\)的光滑代理損失（可加上任意乘性常數縮放及加性常數平移），其中對平方代理損失而言\(F(f) = \frac{1}{2}f^2\)，可驗證此時

對logistic代理損失而言\(F(f) = 2\log (e^{f/2} + e^{-f/2})\)，可驗證此時

我們假設\(F\)為偶函數且\(\beta-\)光滑（\(\beta > 0\)）這意味着對於所有的\(f \in \mathcal{F}\)和\(\alpha \in \mathbb{R}\)，有

注 這裏的一種證明方法是使用Fenchel共軛^[7]\(F^*: \mathcal{F}\rightarrow\mathbb{R}\)，它是\((1/\beta)\)-強凸的。我們有

\[\begin{aligned} &F(f) - \alpha f(x) - \inf_{f\in \mathcal{F}}\left\{F(f) - \alpha f\right\}\\ &= \underbrace{F(f) }_{\sup_{\alpha\in \mathbb{R}}\left\{f\alpha - F^*(\alpha)\right\}}- \alpha f(x) + \underbrace{\sup_{f\in \mathcal{F}}\left\{\alpha f - F(f)\right\}}_{F^*(\alpha)}\\ &= F^*(\alpha) - f(x)\alpha + \sup_{\alpha\in \mathbb{R}}\left\{f(x)\alpha - F^*(\alpha)\right\}\\ &= F^*(\alpha) - f(x)\alpha - \inf_{\alpha\in \mathbb{R}}\left\{F^*(\alpha) - f(x)\alpha \right\}\\ &\geqslant \frac{1}{2\beta}\lVert \alpha - F^{\prime}(f)\rVert^2 \end{aligned} \]

其中\(F^{\prime}(f) = \inf_{\alpha\in \mathbb{R}}\left\{F^*(\alpha) - f(x)\alpha\right\}\)。

由\(\Phi(f) = F(f) - f\)且\(F(f)\)為偶函數，代入可得\(C_{\Phi}(f) = \eta\Phi(f) + (1 - \eta)\Phi (-f) = F(f) - (2\eta - 1)f(x)\)，因此

這將得出\(\Gamma(t) = \sqrt{2\beta t} = \mathcal{O}(\sqrt{t})\)的代理損失函數的超額風險界：

hinge損失^[5]

對hinge損失\(\Phi(f) = (1-f)+ = \max\left\{1-f, 0\right\}\)，我們有

接下來我們來表示\(C^*_{\phi}\)，而這需要對\(\eta(x)\)的取值情況進行分類討論：

1. \(\eta(x) = \frac{1}{2}\): \(f^*_{\Phi}(x) = c \in [-1, 1]\)，\(C^*_{\Phi} = \frac{1}{2}(1-f) + \frac{1}{2}(1+f) = 1\)。

2. \(\eta(x) > \frac{1}{2}\): \(f^*(x) = 1\)，\(C^*_{\Phi} = 2(1 - \eta)\)。

3. \(\eta(x) < \frac{1}{2}\): \(f^*(x) = -1\)，\(C^*_{\Phi} = 2\eta\)。

綜上所述，\(C^*_{\Phi} = 2\min\left\{\eta, 1 - \eta\right\}\)。

於是

接下來我們需要對\(\eta(x)\)和\(f(x)\)的取值情況進行分類討論：

1. \(\eta(x) = \frac{1}{2}\):
   此時\(C_{\text{0-1}}(f) - C^*_{\text{0-1}} = 0\)，故必有\(C_{\Phi}(f) - C^*_{\Phi} \geqslant C_{\text{0-1}}(f) - C^*_{\text{0-1}}\)。

2. \(\eta(x) > \frac{1}{2}\):

   此時\(C^*_{\Phi} = 2( 1- \eta)\)，\(C_{\text{0-1}}(f) - C^*_{\text{0-1}} = \left(2\eta - 1\right)\Phi_{\text{0-1}}\left(f\right)\)。

   a. 當\(f(x) < -1\)時，

   \[\begin{aligned} C_{\Phi}(f) - C^*_{\Phi} &= \eta(1 - f) - 2(1 - \eta) \\ &= 2\eta - 1 - \underbrace{\left(1 - \eta(1 - f)\right)}_{<0}\\ &\geqslant 2\eta - 1\\ &= C_{\text{0-1}}(f) - C^*_{\text{0-1}} \end{aligned} \]

   b. 當\(-1 \leqslant f(x) \leqslant 1\)時，

   \[\begin{aligned} C_{\Phi}(f) - C^*_{\Phi} &= 1 + (1 - 2\eta) f - 2(1 - \eta) \\ &= 2\eta - 1 - \underbrace{(2\eta - 1)f}_{b(f)}\\ &= |2\eta - 1 - b(f)|\\ &\geqslant C_{\text{0-1}}(f) - C^*_{\text{0-1}} \end{aligned} \]

   c. 當\(f(x) > 1\)時，此時\(C_{\text{0-1}}(f) - C^*_{\text{0-1}} = 0\)。故必有\(C_{\Phi}(f) - C^*_{\Phi} \geqslant C_{\text{0-1}}(f) - C^*_{\text{0-1}}\)。

3. \(\eta < \frac{1}{2}\): 類似地，有\(C_{\Phi}(f) - C^*_{\Phi} \geqslant C_{\text{0-1}}(f) - C^*_{\text{0-1}}\)。

綜上所述，代理損失函數的超額風險界對於\(\Gamma\)為恆等函數時成立（也即\(\Gamma(t) = t = \mathcal{O}(t)\)）。換句話説，對於hinge損失，我們有

也就意味着超額\(\Phi\)-風險直接控制超額0-1風險。

對於同樣的二分類問題，可以使用不同的凸代理。儘管貝葉斯分類器總是相同的（即\(h^* = \mathrm{sign}(2\eta - 1)\)），但大部分代理風險的最小點\(f^*\)是不同的。例如，對於hinge損失，\(f^*\)正好為\(\mathrm{sign}(2\eta - 1)\)，然而對於諸如形式為\(\Phi(f) = F(f) - f\)的損失，我們有\(F^{\prime}(f) = 2\eta - 1\)，因此對於平方損失，\(f^* = 2\eta - 1\)；對於logistic損失，可以驗證\(f^* = 2 \text{atanh}(2\eta - 1)\)（其中\(\text{atanh}\)表示雙曲反正切）。

注 當函數空間\(\mathcal{F}\)足夠靈活以致\(f\in\mathcal{F}\)可以達到代理風險\(R_{\Phi}\)的最小點時，例如核方法或帶有足夠多神經元的神經網絡，最小的0-1風險\(R^*_{\text{0-1}}\)是可達的。

然而在實踐中，尤其在高維的情況下，使用受限的模型類，尤其是線性模型，達到最小代理風險將不再可能。在這種情況下，我們可以定義基於模型類的一致性^[8]（關於這個可以參見我的博客《學習理論：預測器-拒絕器多分類棄權學習 》）。

5 超額風險的分解

考慮最小化代理損失函數的超額風險\(R_{\Phi}(\hat{f}) - R_{\Phi}^{*}\)，這裏\(\hat{f}\)做為\(f^*\)的估計值，是最小化如下所示的經驗誤差（泛化誤差的近似）^[9]來獲得的：

而這裏的超額風險可以進一步做如下分解^[5]：

其中\(\inf_{f\in\mathcal{F}}R_{\Phi}(f)\)為假設類最優（best-in-class）誤差，對應的假設類最優假設記為\(f^{\circ}\)，假設類最優誤差也可以記為\(R_{\Phi}(f^{\circ})\)

• 第一項差值被稱為估計誤差（estimation error），它衡量了一個模型和假設類最優的模型之間的差距。

• 第二項差值是逼近誤差（approximation error），代表了假設類\(\mathcal{F}\)在多大程度上涵蓋了最優實值輸出函數\(f^*\)，刻畫了模型的表達能力。

接下來我們分別來看逼近誤差和估計誤差。

6 逼近誤差

逼近誤差\(\inf_{f\in\mathcal{F}}R_{\Phi}(f) - R_{\Phi}^{*}\)是確定性的，它依賴於潛在的分佈及函數類\(\mathcal{F}\)：函數類越“大”，逼近誤差越小。

界定逼近誤差需要貝葉斯預測器\(f^*\)的假設，因此也需要在測試分佈上的假設。

在本部分，我們關注\(\mathcal{F}=\left\{f_{\theta}, \theta\in \Theta\right\}(\Theta\subset \mathbb{R}^d)\)，以及凸Lipschitz連續的代理損失\(\Phi(\cdot)\)，並假設\(\theta^*\)是\(R_{\Phi}(f_{\theta})\)在\(\theta \in \mathbb{R}^d\)的最小點，假設該最小點存在（\(\theta^*\)常常並不屬於\(\Theta\)）。這也就意味着逼近誤差可以被分解為

• 第二項\(\inf_{\theta\in\mathbb{R}^d}R_{\Phi}(f_{\theta}) - R_{\Phi}^{*}\)是由所選擇的模型\(f_{\theta}\)的集合產生的不可壓縮近似誤差。對於諸如核方法或神經網絡的靈活模型，這個不可壓縮誤差可以根據需要變小。

• 函數\(\theta\mapsto R_{\Phi}(f_{\theta}) - \inf_{\theta\in\mathbb{R}^d}R_{\Phi}(f_{\theta})\)在\(\mathbb{R}^d\)上非負，且通常可以被特定的範數\(\Omega(\theta - \theta^*)\)（或其平方）界定，因此我們可以將上述的第一項\(\inf_{\theta\in\mathcal{\Theta}}R_{\Phi}(f_{\theta}) - \inf_{\theta\in\mathbb{R}^d}R_{\Phi}(f_{\theta})\)看做是\(\theta^*\)和\(\Theta\)之間某種“距離”的體現。

如果代理損失函數是\(G\)-Lipschitz連續的，即存在常數\(G > 0\)，對任意\(u_1, u_2 \in \mathbb{R}\),都有\(\left|\Phi(u_1) - \Phi(u_2)\right| \leqslant G\left|u_1 - u_2\right|\)成立（參見我的博客《數值優化：算法分類及收斂性分析基礎》）， 我們有

因此，逼近誤差的第一部分被\(G\)和\(f_{\theta^{*}}\)和\(\mathcal{F}=\left\{f_{\theta}, \theta\in \Theta\right\}\)之間的某種“距離”之積所界定，這裏是指某種偽距離\((\theta_1, \theta_2)\mapsto \mathbb{E}\left[|f_{\theta_1}(x) - f_{\theta_2}(x)|\right]\)（忽略當且僅當\(\theta = \theta^{\prime}\)時該式為0這一性質）。

7 估計誤差

機器學習理論的一大目標是最小化估計誤差\(R_{\Phi}(\hat{f}) - \underset{f\in\mathcal{F}}{\inf} R_{\Phi}(f)\)，然而我們前面提到過，\(\hat{f}\)做為\(f^*\)的估計值，是最小化經驗誤差來獲得的，即\(\hat{f} = \underset{f\in \mathcal{F}}{\inf}\widehat{R}_{\Phi}(f)\)。這也就意味着\(\hat{f}\)並不能保證最小化泛化誤差\(R_{\Phi}(\hat{f})\)，自然也就無法保證最小化估計誤差了。

於是，考慮對估計誤差進行進一步的分解^[5]與界定：

觀察上式，我們可以發現：

• 移除\(\widehat{R}_{\Phi}\)和\(\hat{f}\)之間統計依賴性的關鍵工具是取一致界（uniform bound），也即上式中的\(\sup_{f\in \mathcal{F}}\left(\cdot\right)\)操作。
• 當\(\hat{f}\)並非\(\widehat{R}_{\Phi}\)的全局最優點但滿足\(\widehat{R}_{\Phi}(\hat{f})\leqslant \inf_{f\in\mathcal{F}}\widehat{R}_{\Phi}(f) + \epsilon\)時，則優化誤差\(\epsilon\)需要被加入本部分所提到的估計誤差中。
• 漸進偏差（uniform deviation） 隨着\(\mathcal{F}\)的“大小”而增長，它是一個隨機量（由於其依賴於數據），並常隨着樣本數量\(m\)衰減。
• 這裏的關鍵問題是我們需要對所有\(f\in \mathcal{F}\)的一致控制：正如我們後面會涉及的，對於單個\(f\)，可以對隨機變量\(\Phi(yf(x))\)應用集中不等式（如Hoeffding不等式）以得到\(\mathcal{O}(1 / \sqrt{m})\)的界。然而，當控制在多個\(f\)上的最大偏差時，會存在其中某個偏差變大的可能。因此，我們需要顯式控制這種現象。

8 估計誤差界

8.1 經驗過程與McDiarmid 不等式的應用

由於估計誤差是一個隨機量，我們需要使用概率工具來界定它，這時界可以以某個高概率成立。而\(\sup_{f\in \mathcal{F}}\lvert \widehat{R}_{\Phi}(f) - R_{\Phi}(f)\lvert\)可以視為函數\(f\in \mathcal{F}\)做為下標索引的隨機過程的量綱（magnitude），這種隨機過程稱為經驗過程（參見我的博客（《學習理論：代理損失函數的泛化界與Rademacher複雜度》）））。於是證明估計誤差有界的問題可轉化為證明經驗過程有界的問題。

設\(A(z_1, \cdots, z_m) = \sup_{f\in \mathcal{F}}\left(\widehat{R}_{\Phi}(f) - R_{\Phi}(f)\right)\)，其中隨機變量\(z_i = (x_i, y_i)\)獨立同分布。假設對於所有的在數據生成分佈的支撐集（support）裏的\((x, y)\)，以及\(f\in \mathcal{F}\)，代理損失函數都位於0和某個\(M_{\Phi}\)之間（對於大部分代理損失函數而言，這是當函數\(f\)有界時的直接結果）。

注 直觀地理解，概率分佈\(p\)的支撐集定義為那些概率大於0的點，對於離散概率分佈而言為\(\left\{x: p(X=x) > 0\right\}\)，對於連續概率分佈而言為\(\left\{x: p(x) > 0\right\}\)^[9]。

對於單個函數\(f\in \mathcal{F}\)，我們可以通過Hoeffding不等式控制\(\widehat{R}_{\Phi}(f)\)與\(R_{\Phi}(f)\)之間的偏差（這是一個有界獨立隨機變量的經驗均值，與其期望之間的偏差）：對於任意\(\delta\in (0, 1)\)，至少以\(1 - \delta\)的概率有

Hoeffding不等式: ^[1][5][10] 若\(X_1, \cdots, X_m\)為獨立隨機變量且\(X_i\in [a, b]\)，則有

\[P\left(\frac{1}{m}\sum_{i=1}^m X_i - \frac{1}{m}\sum_{i=1}^m\mathbb{E}[X] \geqslant \epsilon\right) \leqslant \exp\left(-\frac{2m\epsilon^2}{(b - a)^2}\right) \]

有時也會用到Hoeffding不等式的另一種表達形式，令\(\delta = \exp\left(-\frac{2m\epsilon^2}{(b - a)^2}\right)\)（\(\Rightarrow \epsilon = \frac{(b - a)}{\sqrt{2m}}\sqrt{\log\frac{1}{\delta}}\)），則至少以\(1 - \delta\)的概率有

\[\frac{1}{m}\sum_{i=1}^m X_i - \frac{1}{m}\sum_{i=1}^m\mathbb{E}[X] \leqslant \frac{(b - a)}{\sqrt{2m}}\sqrt{\log\frac{1}{\delta}} \]

這個控制可以擴展到多個函數\(f\)。這裏需要用到McDiarmid不等式，而該不等式的應用以有界變差條件為前提，在這裏即當將單個變量\(z_i\in \mathcal{X}\times\mathcal{Y}\)替換為與訓練集獨立同分布的\(z_i^{\prime}\in \mathcal{X}\times\mathcal{Y}\)後，偏差最多為\(\frac{1}{m}M_{\Phi}\)（也即\(\left|A(z_1, \cdots, z_m) - A(z_1, \cdots, z_i^{'}, \cdots, z_m)\right|\leqslant \frac{1}{m}M_{\Phi}\)成立，類似的證明可以參見我的博客《學習理論：代理損失函數的泛化界與Rademacher複雜度》）。於是，應用McDiarmid不等式可以得到：至少以\(1 - \delta\)的概率有

因此，要證明經驗過程有界，可以先界定\(\sup_{f\in \mathcal{F}} \left(\widehat{R}_{\Phi}(f) - R_{\Phi}(f)\right)\)的期望（或相似的量\(\sup_{f\in \mathcal{F}} \left(R_{\Phi}(f) - \widehat{R}_{\Phi}(f)\right)\)的期望，它們通常具有同樣的界），然後將單側界轉換為帶\(\left|\cdot\right|\)的雙側界即可。而這個期望的界定可以使用模型類的Rademacher複雜度（參見我之前的博客）。

8.2 簡化情形： 有限數量的模型

對於有限數量的模型，可以直接將對多個函數的處理轉換為單個函數\(f\)的處理。在這部分我們假設代理損失函數被界定在0和\(M_{\Phi}\)之間。我們可以使用 聯合界（union bound） 將一致偏差界定：

因此，對於固定的\(f\in \mathcal{F}\)，\(\widehat{R}_{\Phi}(f)\)，可以應用雙側Hoeffding's不等式來界定每一個\(\mathbb{P}\left(\left|\widehat{R}_{\Phi}(f) - R_{\Phi}(f)\right| \geqslant \epsilon\right)\)以得到

雙側Hoeffding不等式: ^[11] 若\(X_1, \cdots, X_m\)為獨立隨機變量且\(X_i\in [a, b]\)，則有

\[P\left(\left|\frac{1}{m}\sum_{i=1}^m X_i - \frac{1}{m}\sum_{i=1}^m\mathbb{E}[X]\right| \geqslant \epsilon\right) \leqslant 2\exp\left(-\frac{2m\epsilon^2}{(b - a)^2}\right) \]

因此，令\(\delta = 2\left|\mathcal{F}\right|\exp(-2mt^2 / M_{\Phi}^2)\)（\(\Rightarrow \epsilon = \frac{M_{\Phi}}{\sqrt{2m}}\sqrt{\log \frac{2\left|\mathcal{F}\right|}{\delta}}\)），得到至少以\(1 - \delta\)的概率有：

其中最後一行不等式我們使用了平方根函數的次可加性（sub-additivity）^[13]。這是一個一致偏差的上界。根據上述界，當模型類“大小”的對數\(\log(\left|\mathcal{F}\right|)\)顯著小於\(m\)時，學習是可能的。這是一個對一致偏差的通用控制方法。

注 這個上界對於有限的模型類成立。

8.3 通過覆蓋數超越有限多的模型

簡單地説，覆蓋數（covering number） ^[1][11]背後的思想是通過無限多的元素來處理函數空間，而這是通過使用有限多的元素來對其進行近似而達到的。這也常被稱為“\(\epsilon\)-網論證”。

這裏我們假設代理損失函數是\(G\)-Lipschitz連續的。因此，正像在第6部分提到過的，對任意\(f_1, f_2\in \mathcal{F}\)，我們有

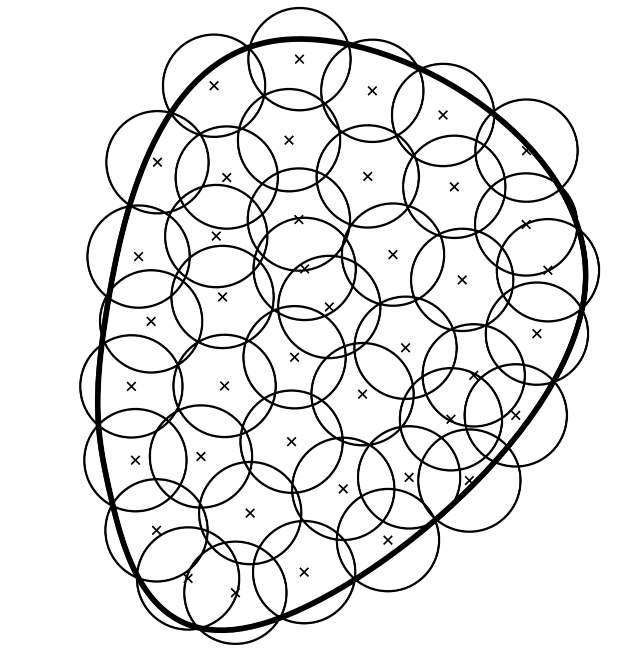
定義（覆蓋數） 我們假設有\(N\)個元素\(f_1, \cdots, f_N\)使得對任意\(f\in \mathcal{F}\)，存在\(i\in \left\{1, \cdots, N\right\}\)，使得\(\Delta(f, f_i)\leqslant \epsilon\)（\(d\)按上式定義）。最小的\(N\)的可能值是\(\mathcal{F}\)在精度為\(\epsilon\)時的覆蓋數（Cover number），記為\(\mathcal{N}(\mathcal{F}, \Delta, \epsilon)\)。下面展示了在二維的情況下使用歐幾里得球的覆蓋：

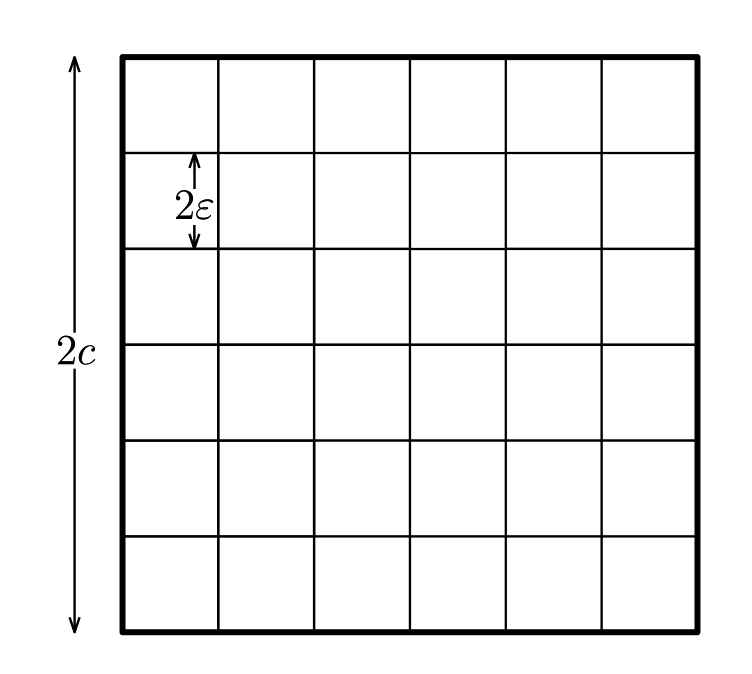
覆蓋數\(\mathcal{N}(\mathcal{F}, \Delta, \epsilon)\)可視為\(\epsilon\)的非增函數。通常情況下，當\(\epsilon\rightarrow 0\)時，\(\mathcal{N}(\mathcal{F}, \Delta, \epsilon)\)隨着\(\epsilon\)以指數\(\epsilon^{-d}\)變化，這裏\(d\)是潛在維度。實際上，對於\(f\)關於\(M_{\Phi}\)的有界條件而言，如果\(\mathcal{F}\)（在某種特定的參數化下）被包含在維度為\(d\)的\(M_{\Phi}\)-球中的半徑為\(c\)的球中，它就可以被\((c/\epsilon)^d\)個長度為\(2\epsilon\)的立方體覆蓋（若\(c \geqslant \epsilon\)），如下圖所示：

推廣到所有在\(d\)維情況下等價的距離\(\Delta\)，對於有限維向量空間的任意有界子集\(\mathcal{F}\)，我們仍然有\(\mathcal{N}(\mathcal{F}, \Delta, \epsilon)\sim \epsilon^{-d}\)，取對數可得\(\log \mathcal{N}(\mathcal{F}, \Delta, \epsilon)\sim d\log\frac{1}{\epsilon}\)。

對於某些集合\(\mathcal{F}\)（例如在\(d\)維情況下關於有界Lipschitz常量的Lipschitz連續函數），\(\log \mathcal{N}(\mathcal{F}, \Delta, \epsilon)\)增長得更快，例如以\(\epsilon^{-d}\)的階增長。

\(\epsilon\)-網論證 給定\(\mathcal{F}\)的一個覆蓋，對所有\(f\in \mathcal{F}\)和與之相關的覆蓋元素\((f_i)_{i\in 1, \cdots, \mathcal{N}(\mathcal{F}, \Delta, \epsilon)}\)，由\(\widehat{R}\)和\(R\)都關於距離\(\Delta\)滿足\(G\)-Lipschitz連續，於是對任意\(i\in \left\{1, \cdots, \mathcal{N}(\mathcal{F}, \Delta, \epsilon)\right\}\)，我們有

由於\((f_i)_{i\in 1, \cdots, \mathcal{N}(\mathcal{F}, \Delta, \epsilon)}\)滿足覆蓋性質，於是我們可以用\(\epsilon\)將\(\Delta(f, f_i)\)界定：

這也就意味着，若使用7.2部分的結論，則以大於\(1 - \delta\)的概率有

因此，若\(\mathcal{N}(\mathcal{F}, \Delta, \epsilon)\sim \epsilon^{-d}\)，忽略常數的話，我們還需要界定\(\epsilon + \sqrt{d\log(1 / \epsilon) / m}\)。取\(\epsilon \propto 1 / \sqrt{m}\)可以得到\(\mathcal{O}\left(\sqrt{(d/m)\log (m)}\right)\)的率。和7.2部分有限模型類的情況有點像，這裏和\(m\)的關係也接近於\(1 / \sqrt{m}\)。然而，除非重新定義覆蓋數的計算或者使用更高級的工具（比如鏈（chaining）），這通常會導致非最優的維度項與/或樣本數量項的出現。

有兩個有力的工具可以以合理的代價導出更好的界，它們是Rademacher複雜度和Gaussian複雜度。其中Rademacher複雜度可以參見我的博客《學習理論：代理損失函數的泛化界與Rademacher複雜度》。

參考

• [1] Bach, Francis. Learning theory from first principles. MIT press, 2024.
• [2] 【COLT 2025】Conference on Learning Theory
• [3] Mohri M, Rostamizadeh A, Talwalkar A. Foundations of machine learning[M]. MIT press, 2018.
• [4] John Duchi: Statistics and Information Theory
• [5] 周志華, 王魏, 高尉, 張利軍. 機器學習理論導引[M]. 機械工業出版社, 2020.
• [6] Han Bao: Learning Theory Bridges Loss Functions
• [7] Boyd, Stephen, and Lieven Vandenberghe. Convex optimization. Cambridge university press, 2004.
• [8] Long, Phil, and Rocco Servedio. "Consistency versus realizable H-consistency for multiclass classification." International conference on machine learning. PMLR, 2013.
• [9] Ni C, Charoenphakdee N, Honda J, et al. On the calibration of multiclass classification with rejection[J]. Advances in Neural Information Processing Systems, 2019, 32.
• [10] Wikipedia: Support (mathematics)
• [11] Vershynin R. High-dimensional probability: An introduction with applications in data science[M]. Cambridge university press, 2018.
• [12] Wikipedia: Subadditivity