遍歷二叉樹一共有四種方式：前序遍歷，中序遍歷，後序遍歷，層序遍歷（廣度優先）

準備

先定義一個結點類（後續代碼需要使用）

public class Node<V> {
    public V value;
    public Node<V> left;
    public Node<V> right;
    public Node(V value) {
        this.value = value;
    }
}

前序遍歷

操作步驟如下：

1. 訪問根結點
2. 遞歸遍歷左子樹
3. 遞歸遍歷右子樹

假設一個二叉樹的結構如下圖所示：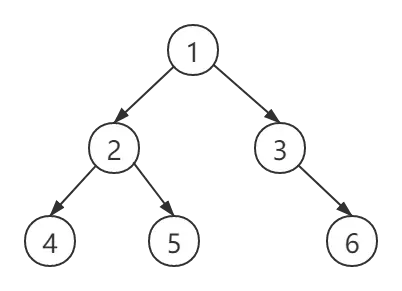
則遍歷結果為：1 2 4 5 3 6
實現方式：

• 遞歸方式

public class PreOrderRecursivelyVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        System.out.println(node.value + " ");
        visit(root.left, output);
        visit(root.right, output);
    }
}

• 非遞歸方式

藉助棧（先進後出）來實現
代碼如下：

public class PreOrderVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        Stack<Node<V>> help = new Stack<>();
        // 1. 根結點入棧
        help.push(root);
        while (!help.isEmpty()) {
            // 2. 棧頂結點出棧
            Node<V> node = help.pop();
            // 3. 訪問出棧結點
            System.out.println(node.value + " ");
            // 4. 依次將該結點的右，左孩子入棧
            if (node.right != null) {
                help.push(node.right);
            }
            if (node.left != null) {
                help.push(node.left);
            }
        }
    }
}

中序遍歷

操作步驟如下：

1. 遞歸遍歷左子樹
2. 訪問根結點
3. 遞歸遍歷右子樹

假設一個二叉樹的結構如下圖所示：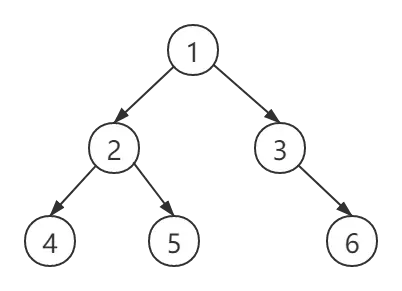
則遍歷結果為：4 2 5 1 3 6
實現方式：

• 遞歸方式

public class InOrderRecursivelyVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        visit(root.left, output);
        System.out.println(node.value + " ");
        visit(root.right, output);
    }
}

• 非遞歸方式

public class InOrderVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        Stack<Node<V>> help = new Stack<>();
        // 定義一個當前結點遍歷並指向根結點
        Node<V> current = root;
        while (current != null || !help.isEmpty()) {
            if (current != null) {
                // 若當前結點不為空，則入棧
                help.push(current);
                // 將當前結點指向該結點的左孩子
                current = current.left;
            } else {
                // 若當前結點為空（即當前已經沒有可訪問的左子樹了），則出棧
                current = help.pop();
                // 訪問出棧結點
                System.out.println(current.value + " ");
                // 將當前結點指向出棧結點的右孩子
                current = current.right;
                // （若該結點存在，則重複執行上面的if分支將該結點的左子樹依次入棧）
            }
        }
    }
}

後序遍歷

操作步驟如下：

1. 遞歸遍歷左子樹
2. 遞歸遍歷右子樹
3. 訪問根結點

假設一個二叉樹的結構如下圖所示：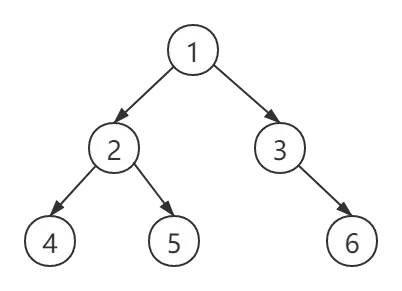
則遍歷結果為：4 5 2 6 3 1
實現方式：

• 遞歸方式

public class PostOrderRecursivelyVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        visit(root.left, output);
        visit(root.right, output);
        System.out.println(node.value + " ");
    }
}

• 非遞歸方式

這種方式稍微複雜一點，因為要先遍歷完左右子樹，再訪問根結點，所以需要知道左右子樹的訪問狀態。

public class PostOrderVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        Stack<Node<V>> help = new Stack<>();
        // 根結點入棧
        help.push(root);
        // top指向棧頂元素
        Node<V> top = null;
        // visited表示剛剛訪問過的結點（初始指向根結點）
        Node<V> visited = root;
        while (!help.isEmpty()) {
            // 獲取棧頂元素，但是不進行出棧操作
            top = help.peek();
            if (top.left != null && top.left != visited && top.right != visited) {
                // 若棧頂元素的左孩子結點存在，且左右孩子都未被訪問過，則左孩子入棧
                help.push(top.left);
            } else if (top.right != null && top.right != visited) {
                // 若棧頂元素的右孩子結點存在，且右孩子未被訪問過，則右孩子入棧
                help.push(top.right);
            } else {
                // 棧頂元素出棧，並訪問該結點
                System.out.println(help.pop().value + " ");
                // 記錄已訪問過的結點
                visited = top;
            }
        }
    }
}

層序遍歷

也可稱為廣度優先遍歷
操作步驟如下：
從上往下，從左至右依次訪問每層的結點
假設一個二叉樹的結構如下圖所示：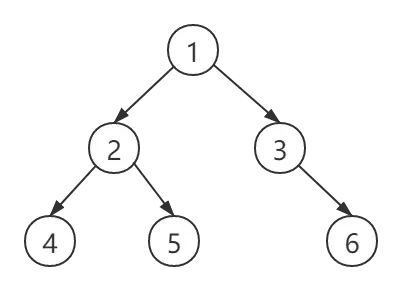
則遍歷結果為：1 2 3 4 5 6
實現方式：
藉助隊列（先進先出）來實現
代碼如下：

public class LevelOrderVisitor {
    public <V> void visit(Node<V> root) {
        if (root == null) {
            return;
        }
        Queue<Node<V>> queue = new LinkedList<>();
        // 根結點進入隊尾
        queue.offer(root);
        while (!queue.isEmpty()) {
            // 出隊列
            Node<V> node = queue.poll();
            // 訪問該結點
            System.out.println(node.value + " ");
            // 依次將該結點的左右孩子入隊列
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }
}

以上就是遍歷二叉樹的幾種方式，完整代碼可查看二叉樹的遍歷。如有錯誤，請指正，謝謝。