2025-11-24:統計計算機解鎖順序排列數。用go語言,給定長度為 n 的數組 complexity,表示編號為 0 到 n-1 的 n 台計算機各自密碼的複雜度(且複雜度兩兩不同)。
編號為 0 的計算機一開始已處於解鎖狀態,作為起點。
其餘每台計算機 i 只能在此前已經解鎖過某台編號為 j 的計算機的情況下被解開,且該 j 必須滿足兩點:j < i 且 complexity[j] < complexity[i](索引和複雜度都比 i 小)。
現在要求統計有多少種由 0..n-1 全排列形成的順序能對應一種合法的解鎖過程(即在排列中,每出現的計算機 i 之前,必然已經出現過至少一個滿足上述條件的 j)。
結果對 1000000007 取模返回。
注意:編號為 0 的計算機一開始就是解鎖的,這並不等同於它在排列中必須位於首位。
2 <= complexity.length <= 100000。
1 <= complexity[i] <= 1000000000。
輸入: complexity = [1,2,3]。
輸出: 2。
解釋:
有效的排列有:
[0, 1, 2]
首先使用根密碼解鎖計算機 0。
使用計算機 0 的密碼解鎖計算機 1,因為 complexity[0] < complexity[1]。
使用計算機 1 的密碼解鎖計算機 2,因為 complexity[1] < complexity[2]。
[0, 2, 1]
首先使用根密碼解鎖計算機 0。
使用計算機 0 的密碼解鎖計算機 2,因為 complexity[0] < complexity[2]。
使用計算機 0 的密碼解鎖計算機 1,因為 complexity[0] < complexity[1]。
題目來自力扣3577。
過程步驟説明
-
初始狀態檢查
計算機0是解鎖過程的起點,一開始就處於解鎖狀態。在排列中,計算機0必須出現在第一個位置。這是因為任何其他計算機i(i > 0)被解鎖時,都需要一個滿足條件的j(j < i 且 complexity[j] < complexity[i])已經出現在排列中。如果計算機0不是第一個出現,那麼第一個出現的計算機i(i ≠ 0)之前不會有任何j出現(因為它是排列首元素),無法滿足解鎖條件,因此排列無效。所以,計算機0必須固定在第一位置。 -
複雜度條件驗證
對於每台計算機i(i從1到n-1),必須滿足complexity[i] > complexity[0]。這是因為計算機0是唯一初始解鎖的計算機,且其索引最小(j=0)。如果存在某個i使得complexity[i] ≤ complexity[0],那麼計算機0無法作為j滿足complexity[j] < complexity[i](因為複雜度相等或不滿足小於關係)。同時,其他可能的j(索引小於i)也可能無法滿足條件(因為解鎖鏈依賴計算機0)。因此,一旦發現某個complexity[i] ≤ complexity[0],直接返回0,表示沒有有效排列。- 例如,在輸入complexity = [1,2,3]中,所有i>0的複雜度(2和3)都大於complexity[0]=1,因此條件滿足。
-
計算有效排列數
如果所有i>0均滿足complexity[i] > complexity[0],則有效排列數就是其餘n-1台計算機(索引1到n-1)的全排列數,即(n-1)!。原因如下:- 計算機0固定在第一位置。
- 對於其他計算機,只要計算機0在排列首位,任意順序排列均有效。因為對於任意i>0,計算機0(j=0)總是滿足j < i且complexity[j] < complexity[i],且計算機0已出現在i之前(因它位於首位)。因此,其他計算機的排列順序沒有額外約束。
- 代碼中通過循環從i=1到n-1,將結果ans依次乘以i(即計算1 × 2 × ... × (n-1)),並對10^9+7取模,得到(n-1)!。
-
結果返回
最終返回計算得到的(n-1)!取模後的值。例如,對於complexity = [1,2,3](n=3),(3-1)! = 2,輸出為2,對應兩個有效排列[0,1,2]和[0,2,1]。
時間複雜度和額外空間複雜度
-
總的時間複雜度:O(n)
算法需要遍歷複雜度數組一次(從索引1到n-1),共n-1次循環。每次循環進行常數時間操作(比較和乘法取模),因此時間複雜度為線性O(n)。 -
總的額外空間複雜度:O(1)
除了輸入的複雜度數組外,算法只使用了固定數量的變量(如ans、i和常量mod),不隨輸入規模n變化,因此額外空間複雜度為常數O(1)。
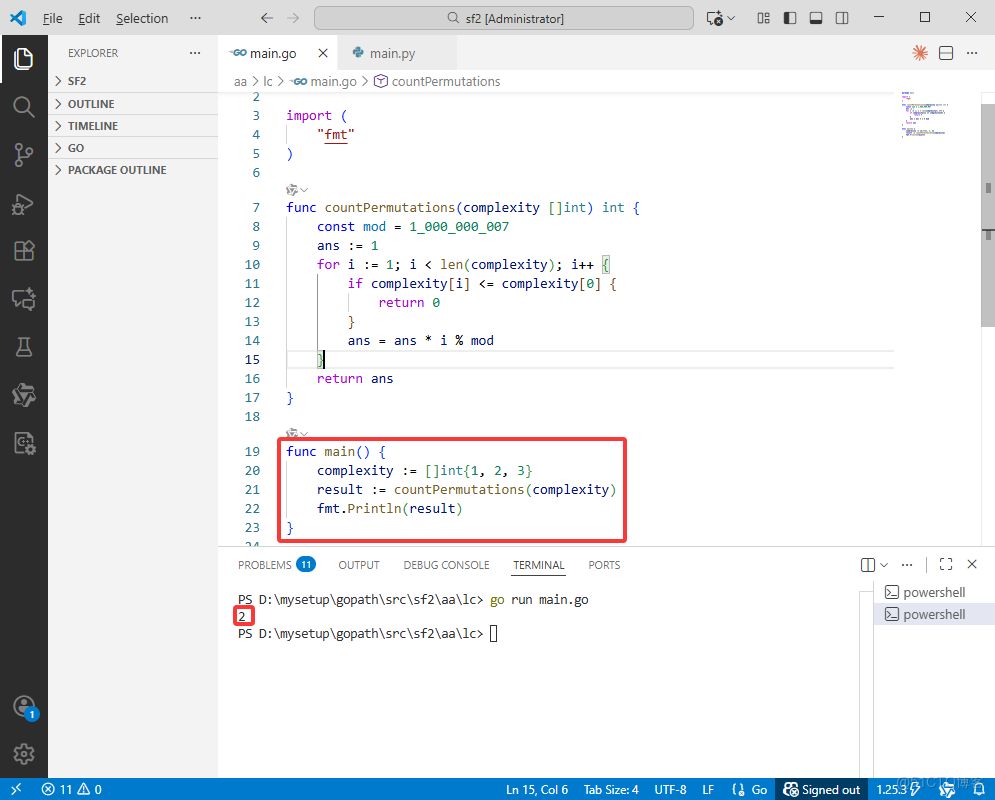
Go完整代碼如下:
package main
import (
"fmt"
)
func countPermutations(complexity []int) int {
const mod = 1_000_000_007
ans := 1
for i := 1; i < len(complexity); i++ {
if complexity[i] <= complexity[0] {
return 0
}
ans = ans * i % mod
}
return ans
}
func main() {
complexity := []int{1, 2, 3}
result := countPermutations(complexity)
fmt.Println(result)
}
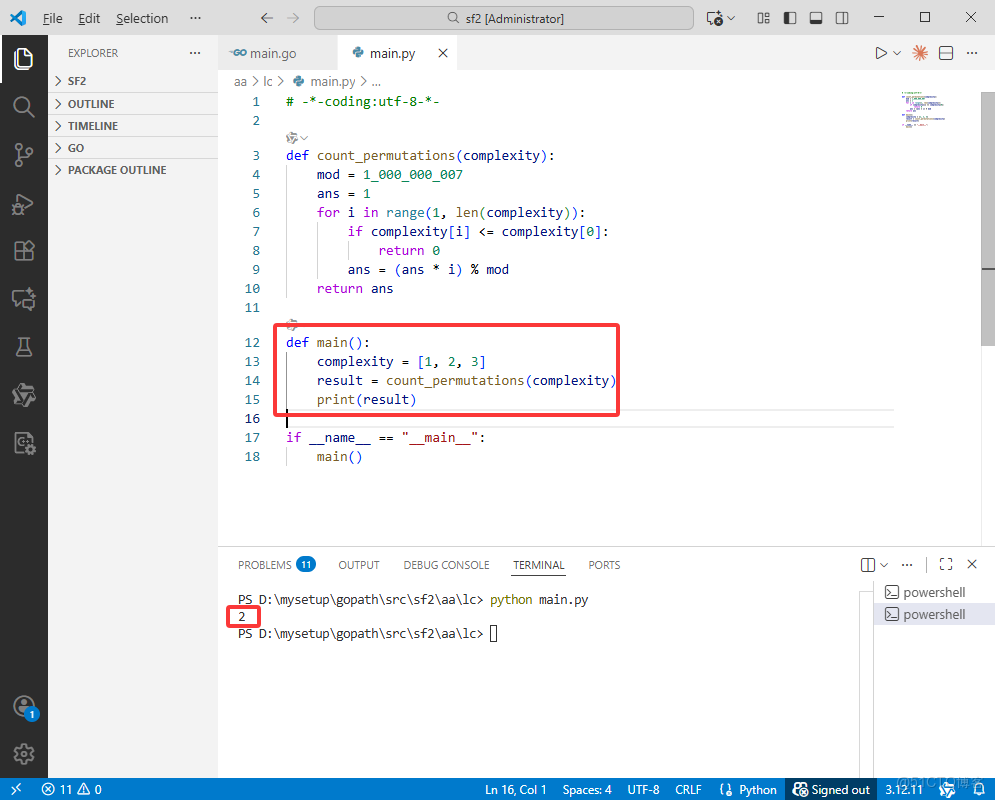
Python完整代碼如下:
# -*-coding:utf-8-*-
def count_permutations(complexity):
mod = 1_000_000_007
ans = 1
for i in range(1, len(complexity)):
if complexity[i] <= complexity[0]:
return 0
ans = (ans * i) % mod
return ans
def main():
complexity = [1, 2, 3]
result = count_permutations(complexity)
print(result)
if __name__ == "__main__":
main()
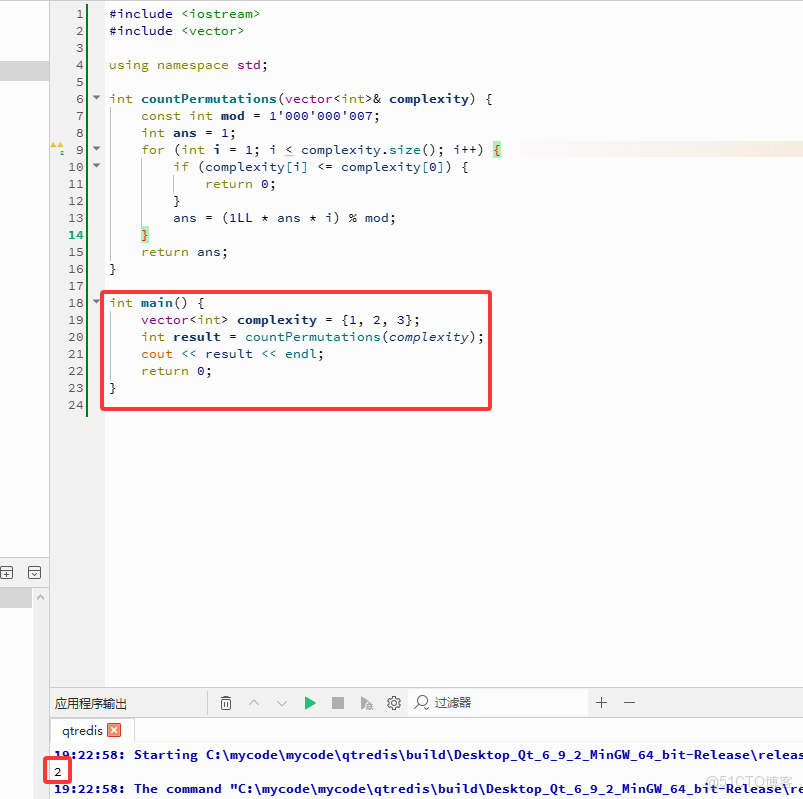
C++完整代碼如下:
#include <iostream>
#include <vector>
using namespace std;
int countPermutations(vector<int>& complexity) {
const int mod = 1'000'000'007;
int ans = 1;
for (int i = 1; i < complexity.size(); i++) {
if (complexity[i] <= complexity[0]) {
return 0;
}
ans = (1LL * ans * i) % mod;
}
return ans;
}
int main() {
vector<int> complexity = {1, 2, 3};
int result = countPermutations(complexity);
cout << result << endl;
return 0;
}