2025-12-28：位計數深度為 K 的整數數目Ⅰ。用go語言，給定兩個正整數 n 和 k。對任意正整數 x，構造數列 a0 = x，ai+1 = f(ai)，其中 f(y) 表示 y 的二進制表示中 1 的個數（例如 f(7)=3，因為 7 的二進制是 111）。反覆應用 f 後，序列必然會落到 1。定義 x 的“二進制1的迭代次數”為使得 ad = 1 的最小非負整數 d（例如 x=7 的序列為 7→3→2→1，因此迭代次數為 3）。

問題是：在區間 [1, n] 內，有多少個正整數的這種迭代次數恰好等於 k？返回該數量。

1 <= n <= 1000000000000000。

0 <= k <= 5。

輸入: n = 4, k = 1。

輸出: 2。

解釋:

在範圍 [1, 4] 中，以下整數的 popcount-depth 恰好等於 1：

x	二進制	序列
2	10	2 → 1
4	100	4 → 1

因此，答案是 2。

題目來自力扣3621。

🔢 問題理解與核心思路

題目要求統計區間 [1, n] 內，有多少個正整數 x 的“位計數深度”（即不斷計算其二進制中1的個數，直到結果為1所需的迭代次數）恰好等於 k。

核心解決思路是：

1. 預處理深度映射：對於任意一個數，其深度只與它二進制表示中1的個數有關。我們可以預先計算出，對於含有 i 個1的數，它的深度是多少。
2. 統計目標數字：利用數位動態規劃，統計在 [1, n] 範圍內，二進制表示中1的個數恰好為 i 的數字有多少個。將這些數字中深度等於 k 的計數累加，即為最終答案。

📝 算法步驟詳解

步驟 1: 特殊情況處理

• 如果 k == 0，根據題目定義，只有深度為0的數滿足條件，這意味着序列從一開始就是1。在區間 [1, n] 中，只有 x=1 滿足條件（因為 f(1)=1），所以直接返回 1。

步驟 2: 將 n 轉化為二進制字符串

• 將輸入的整數 n 轉換為它的二進制字符串表示，例如 n=4 得到字符串 "100"。這樣做是為了方便後續的數位DP處理，可以逐位確定數字。

步驟 3: 預處理深度關係

• 創建一個數組 f，f[i] 表示一個二進制表示中有 i 個1的數字，它的位計數深度是多少。
• 計算方式利用了遞歸關係：一個數的深度，等於它進行一次 popcount 操作後得到的那個數的深度再加1。即 f[i] = f[bits.OnesCount(i)] + 1。
• 初始條件是 f[1] = 0，因為數字1的二進制只有一個1，它本身就已經是1，不需要迭代。
• 然後，我們遍歷所有可能的1的個數 i（從1到二進制字符串的長度 m），如果 f[i] == k，説明所有恰好有 i 個1的數都滿足深度要求，我們需要統計這類數的個數。

步驟 4: 數位動態規劃統計數量

• 這是算法的核心部分，目標是統計在 [1, n] 範圍內，二進制表示中恰好有 targetOnes 個1的數字的個數（其中 targetOnes 是上一步中找出的那些使深度等於 k 的1的個數）。
• 記憶化DFS：定義一個DFS函數，其參數包括：
  • i: 當前正在處理二進制字符串的第幾位（從0開始）。
  • left1: 在剩餘的位數中，還需要放置多少個1。
  • isLimit: 一個布爾值，表示之前確定的位是否完全和 n 的對應位一致。如果為真，則當前位最大隻能取 n 在該位的值（0或1）；如果為假，則當前位可以自由取0或1。
• DFS過程：
  1. 到達終點：如果已經處理完所有位 (i == m)，則檢查是否恰好用完了所需的1的個數 (left1 == 0)。如果是，則找到一個有效數字，返回1；否則返回0。
  2. 記憶化加速：如果當前狀態不受上限限制 (isLimit 為假)，並且這個狀態 (i, left1) 之前已經計算過，則直接返回緩存的結果，避免重複計算。
  3. 確定當前位選擇範圍：根據 isLimit 確定當前位能選擇的最大數字 up。
  4. 枚舉與統計：嘗試在當前位放入 d（0或1），但不能超過 up，並且放入1的總數不能超過 left1。將後續狀態的結果累加。
• 通過調用 dfs(0, targetOnes, true) 啓動統計過程。

步驟 5: 彙總結果

• 對所有滿足 f[i] == k 的 i，調用數位DP統計出二進制中恰好有 i 個1的數字個數，並將這些個數累加，得到最終答案。

⏱️ 複雜度分析

• 時間複雜度：**O(log²n)**。

  1. 預處理深度數組 f 的時間複雜度為 O(log n)，因為 n 的二進制長度 m 約為 log₂n。
  2. 數位DP是主要開銷。DP狀態數量由“當前處理到的位置”和“剩餘需要的1的個數”決定，規模為 O(m * m) = O(log²n)。每個狀態的計算是常數時間。因此，總時間複雜度為 **O(log²n)**。

• 空間複雜度：O(log²n)。 空間消耗主要來自數位DP的記憶化數組 memo，其大小也是 O(m * m) = O(log²n)。深度數組 f 等輔助空間為 O(log n)，因此總空間複雜度為 **O(log²n)**。

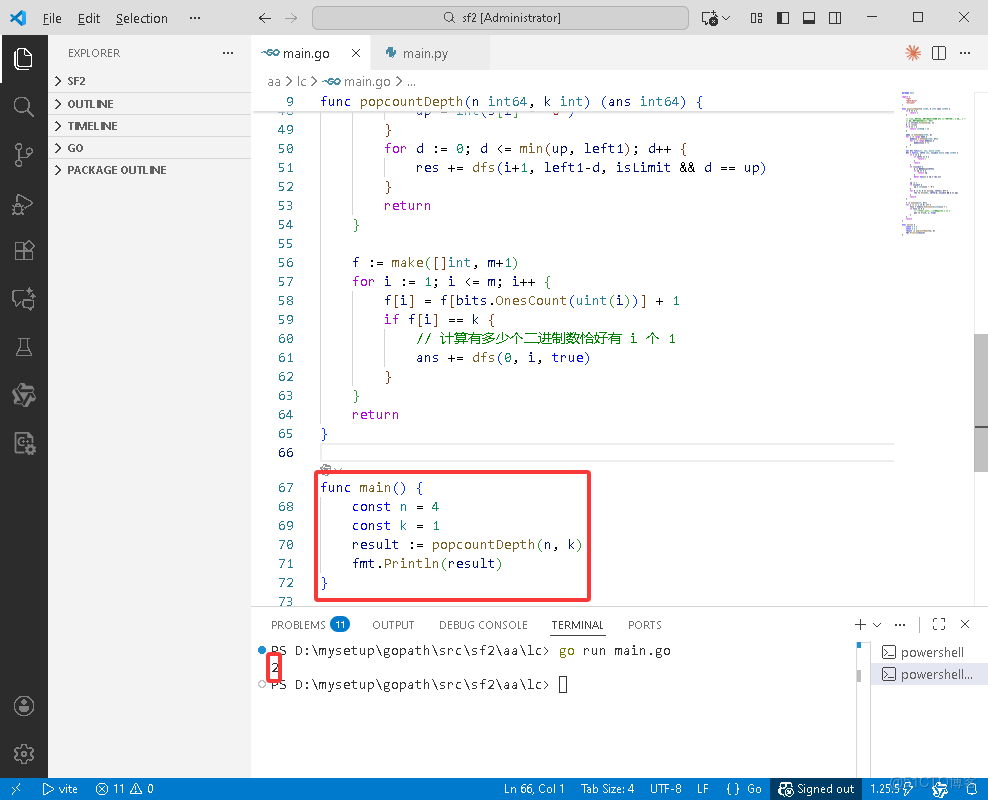
Go完整代碼如下：

package main

import (
	"fmt"
	"math/bits"
	"strconv"
)

func popcountDepth(n int64, k int) (ans int64) {
	if k == 0 {
		return 1
	}

	// 注：也可以不轉成字符串，下面 dfs 用位運算取出 n 的第 i 位
	// 但轉成字符串的通用性更好
	s := strconv.FormatInt(n, 2)
	m := len(s)
	if k == 1 {
		return int64(m - 1)
	}

	memo := make([][]int64, m)
	for i := range memo {
		memo[i] = make([]int64, m+1)
		for j := range memo[i] {
			memo[i][j] = -1
		}
	}

	var dfs func(int, int, bool) int64
	dfs = func(i, left1 int, isLimit bool) (res int64) {
		if i == m {
			if left1 == 0 {
				return 1
			}
			return
		}
		if !isLimit {
			p := &memo[i][left1]
			if *p >= 0 {
				return *p
			}
			defer func() { *p = res }()
		}

		up := 1
		if isLimit {
			up = int(s[i] - '0')
		}
		for d := 0; d <= min(up, left1); d++ {
			res += dfs(i+1, left1-d, isLimit && d == up)
		}
		return
	}

	f := make([]int, m+1)
	for i := 1; i <= m; i++ {
		f[i] = f[bits.OnesCount(uint(i))] + 1
		if f[i] == k {
			// 計算有多少個二進制數恰好有 i 個 1
			ans += dfs(0, i, true)
		}
	}
	return
}

func main() {
	const n = 4
	const k = 1
	result := popcountDepth(n, k)
	fmt.Println(result)
}

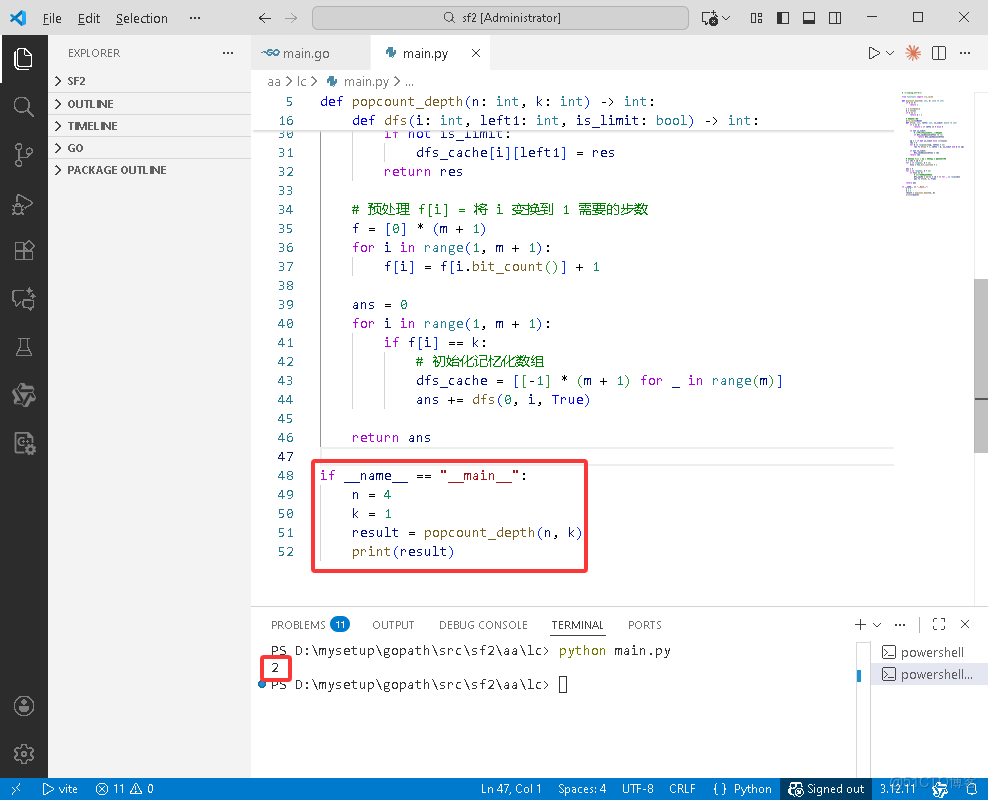
Python完整代碼如下：

# -*-coding:utf-8-*-

from functools import lru_cache

def popcount_depth(n: int, k: int) -> int:
    if k == 0:
        return 1
    
    s = bin(n)[2:]
    m = len(s)
    if k == 1:
        return m - 1
    
    # 記憶化搜索
    @lru_cache(None)
    def dfs(i: int, left1: int, is_limit: bool) -> int:
        if i == m:
            return 1 if left1 == 0 else 0
        
        if not is_limit:
            # 非限制狀態下可以使用記憶化
            if dfs_cache[i][left1] != -1:
                return dfs_cache[i][left1]
        
        up = 1 if not is_limit else int(s[i])
        res = 0
        for d in range(min(up, left1) + 1):
            res += dfs(i + 1, left1 - d, is_limit and d == up)
        
        if not is_limit:
            dfs_cache[i][left1] = res
        return res
    
    # 預處理 f[i] = 將 i 變換到 1 需要的步數
    f = [0] * (m + 1)
    for i in range(1, m + 1):
        f[i] = f[i.bit_count()] + 1
    
    ans = 0
    for i in range(1, m + 1):
        if f[i] == k:
            # 初始化記憶化數組
            dfs_cache = [[-1] * (m + 1) for _ in range(m)]
            ans += dfs(0, i, True)
    
    return ans

if __name__ == "__main__":
    n = 4
    k = 1
    result = popcount_depth(n, k)
    print(result)

C++完整代碼如下：

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <cstring>

using namespace std;

class Solution {
private:
    long long dfs(int i, int left1, bool isLimit, int m, const string& s,
                  vector<vector<long long>>& memo) {
        if (i == m) {
            return left1 == 0 ? 1 : 0;
        }

        if (!isLimit && memo[i][left1] != -1) {
            return memo[i][left1];
        }

        int up = isLimit ? (s[i] - '0') : 1;
        long long res = 0;

        for (int d = 0; d <= min(up, left1); d++) {
            res += dfs(i + 1, left1 - d, isLimit && d == up, m, s, memo);
        }

        if (!isLimit) {
            memo[i][left1] = res;
        }
        return res;
    }

public:
    long long popcountDepth(long long n, int k) {
        if (k == 0) {
            return 1;
        }

        // 將n轉換為二進制字符串
        string s;
        while (n > 0) {
            s = char('0' + (n & 1)) + s;
            n >>= 1;
        }
        int m = s.size();

        if (k == 1) {
            return m - 1;
        }

        // 計算f數組
        vector<int> f(m + 1, 0);
        for (int i = 1; i <= m; i++) {
            f[i] = f[__builtin_popcount(i)] + 1;
        }

        long long ans = 0;

        // 對每個滿足f[i]==k的i進行計算
        for (int i = 1; i <= m; i++) {
            if (f[i] == k) {
                // 為每個i創建新的記憶化數組
                vector<vector<long long>> memo(m, vector<long long>(m + 1, -1));
                ans += dfs(0, i, true, m, s, memo);
            }
        }

        return ans;
    }
};

int main() {
    long long n = 4;
    int k = 1;

    Solution solution;
    long long result = solution.popcountDepth(n, k);
    cout << result << endl;

    return 0;
}