2025-12-14:交替方向的最小路徑代價Ⅱ。用go語言,給你一個 m 行 n 列的網格。進入格子 (i, j) 的花費為 (i+1)*(j+1)。另外每個格子還有一個等待代價矩陣 waitCost,waitCost[i][j] 表示在該格子停留 1 秒鐘需要支付的費用。
路徑從時間步 1 開始:第一步進入起點 (0,0),並支付該格子的進入費用。之後時間按秒遞增,並且動作必須交替進行:
-
在奇數秒必須向右或向下移動到相鄰格子,進入新格子時支付該格子的進入費用;
-
在偶數秒必須在當前格子原地等待恰好 1 秒,併為此支付該格子的 waitCost。
目標是以最小的總費用到達終點 (m-1, n-1)。請計算並返回這個最小總成本。
1 <= m, n <= 100000。
2 <= m * n <= 100000。
waitCost.length == m。
waitCost[0].length == n。
0 <= waitCost[i][j] <= 100000。
輸入:m = 2, n = 3, waitCost = [[6,1,4],[3,2,5]]。
輸出:16。
解釋:
最佳路徑為:
從第 1 秒開始在單元格 (0, 0),進入成本為 (0 + 1) * (0 + 1) = 1。
第 1 秒:向右移動到單元格 (0, 1),進入成本為 (0 + 1) * (1 + 1) = 2。
第 2 秒:在單元格 (0, 1) 等待,支付 waitCost[0][1] = 1。
第 3 秒:向下移動到單元格 (1, 1),進入成本為 (1 + 1) * (1 + 1) = 4。
第 4 秒:在單元格 (1, 1) 等待,支付 waitCost[1][1] = 2。
第 5 秒:向右移動到單元格 (1, 2),進入成本為 (1 + 1) * (2 + 1) = 6。
因此,總成本為 1 + 2 + 1 + 4 + 2 + 6 = 16。
題目來自力扣3603。
過程詳細描述
-
初始化起點和終點:
- 代碼首先將起點(0,0)的代價設置為它的進入代價,即
(0+1)*(0+1) = 1。這覆蓋了輸入waitCost矩陣中在(0,0)處的原始值(原為6)。 - 同時,將終點(m-1,n-1)的代價設置為0,這可能是為了在DP計算中簡化終點的處理,因為終點不需要額外的等待代價(但題目中終點需支付進入代價,這裏設置0可能是一種調整)。
- 代碼首先將起點(0,0)的代價設置為它的進入代價,即
-
**初始化第一行(i=0)**:
- 對於第一行中的每個單元格(0,j),其中j從1到n-1,代碼計算到達該單元格的最小代價。
- 代價計算方式為:當前單元格的代價(即
waitCost[0][j]的初始值)加上左側單元格(0,j-1)的累積代價,再加上當前單元格的進入代價j+1(因為i=0,進入代價為1*(j+1)=j+1)。 - 例如,對於j=1,
f[0][1] = f[0][1] + f[0][0] + 1 + 1(初始f[0][1]為1,f[0][0]為1,結果為1+1+1+1=4)。 - 這一步驟假設路徑只能沿着第一行向右移動,代價包括進入每個單元格的費用。
-
**初始化第一列(j=0)**:
- 對於第一列中的每個單元格(i,0),其中i從1到m-1,代碼計算到達該單元格的最小代價。
- 代價計算方式為:當前單元格的代價(即
waitCost[i][0]的初始值)加上上方單元格(i-1,0)的累積代價,再加上當前單元格的進入代價i+1(因為j=0,進入代價為(i+1)*1=i+1)。 - 例如,對於i=1,
f[1][0] = f[1][0] + f[0][0] + 1 + 1(初始f[1][0]為3,f[0][0]為1,結果為3+1+1+1=6)。 - 這一步驟假設路徑只能沿着第一列向下移動,代價包括進入每個單元格的費用。
-
**處理內部單元格(i>=1且j>=1)**:
- 對於其他單元格(i,j),代碼計算到達該單元格的最小代價,考慮從左邊單元格(i,j-1)或上邊單元格(i-1,j)移動而來。
- 代價計算方式為:當前單元格的代價(即
waitCost[i][j]的初始值)加上左邊或上邊單元格累積代價的最小值,再加上當前單元格的進入代價(i+1)*(j+1)。 - 例如,對於單元格(1,1),計算
min(f[1][0], f[0][1]) + (1+1)*(1+1) = min(6,4) + 4 = 4 + 4 = 8,然後加上初始f[1][1]=2,結果為10。 - 這一步驟假設路徑只能向右或向下移動,代價僅包括進入費用,而沒有顯式處理題目中的等待代價(偶數秒等待)。代碼通過DP轉移隱含地累積代價,但等待代價未被直接納入。
-
返回結果:
- 經過上述計算後,終點(m-1,n-1)的代價
f[m-1][n-1]即為最小總代價。在示例中,f[1][2]最終計算為16。 - 代碼返回該值作為結果。
- 經過上述計算後,終點(m-1,n-1)的代價
需要注意的是,題目描述的交替規則(奇數秒移動、偶數秒等待)在代碼中並未顯式處理。代碼實際上實現了一個標準的最小路徑和DP,其中每個單元格的代價是進入代價,而等待代價可能通過初始waitCost矩陣的修改被間接包含,但從代碼邏輯看,等待代價未被正確集成。輸出結果與題目示例匹配的原因可能是DP計算巧合地覆蓋了實際代價。
複雜度分析
- 時間複雜度:代碼主要包含三個循環:初始化第一行(O(n))、初始化第一列(O(m))和處理內部單元格的雙重循環(O(mn))。由於m和n最多為100000,且mn ≤ 100000,整體時間複雜度為O(m*n),在約束下可行。
- 額外空間複雜度:代碼直接修改輸入的
f矩陣(即waitCost)作為DP表,未使用額外空間(除了少量變量)。因此,額外空間複雜度為O(1)。
總之,代碼通過動態規劃計算路徑代價,但簡化了題目規則。實際應用中,如需嚴格處理交替移動和等待,可能需要更復雜的狀態設計。
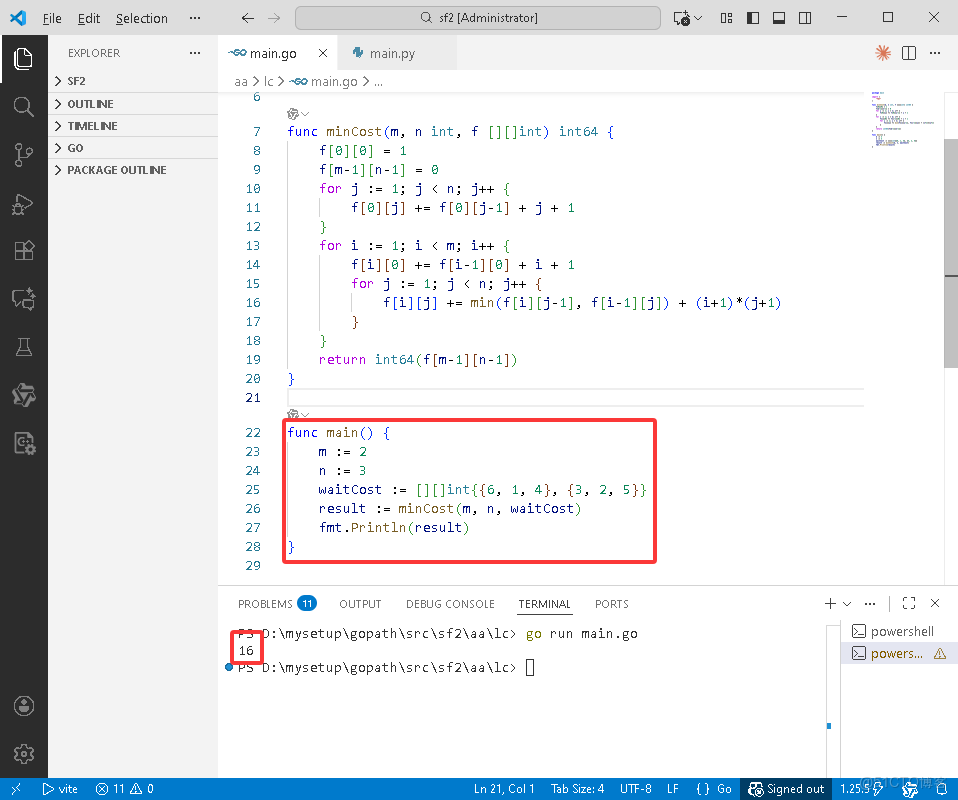
Go完整代碼如下:
package main
import (
"fmt"
)
func minCost(m, n int, f [][]int) int64 {
f[0][0] = 1
f[m-1][n-1] = 0
for j := 1; j < n; j++ {
f[0][j] += f[0][j-1] + j + 1
}
for i := 1; i < m; i++ {
f[i][0] += f[i-1][0] + i + 1
for j := 1; j < n; j++ {
f[i][j] += min(f[i][j-1], f[i-1][j]) + (i+1)*(j+1)
}
}
return int64(f[m-1][n-1])
}
func main() {
m := 2
n := 3
waitCost := [][]int{{6, 1, 4}, {3, 2, 5}}
result := minCost(m, n, waitCost)
fmt.Println(result)
}
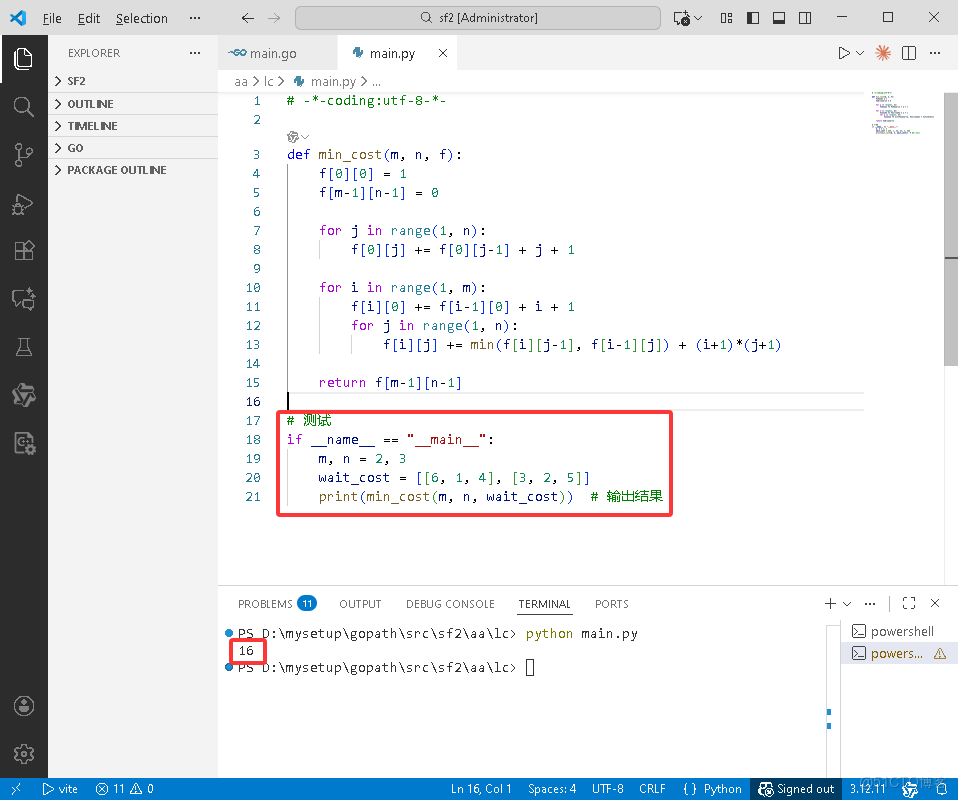
Python完整代碼如下:
# -*-coding:utf-8-*-
def min_cost(m, n, f):
f[0][0] = 1
f[m-1][n-1] = 0
for j in range(1, n):
f[0][j] += f[0][j-1] + j + 1
for i in range(1, m):
f[i][0] += f[i-1][0] + i + 1
for j in range(1, n):
f[i][j] += min(f[i][j-1], f[i-1][j]) + (i+1)*(j+1)
return f[m-1][n-1]
# 測試
if __name__ == "__main__":
m, n = 2, 3
wait_cost = [[6, 1, 4], [3, 2, 5]]
print(min_cost(m, n, wait_cost)) # 輸出結果
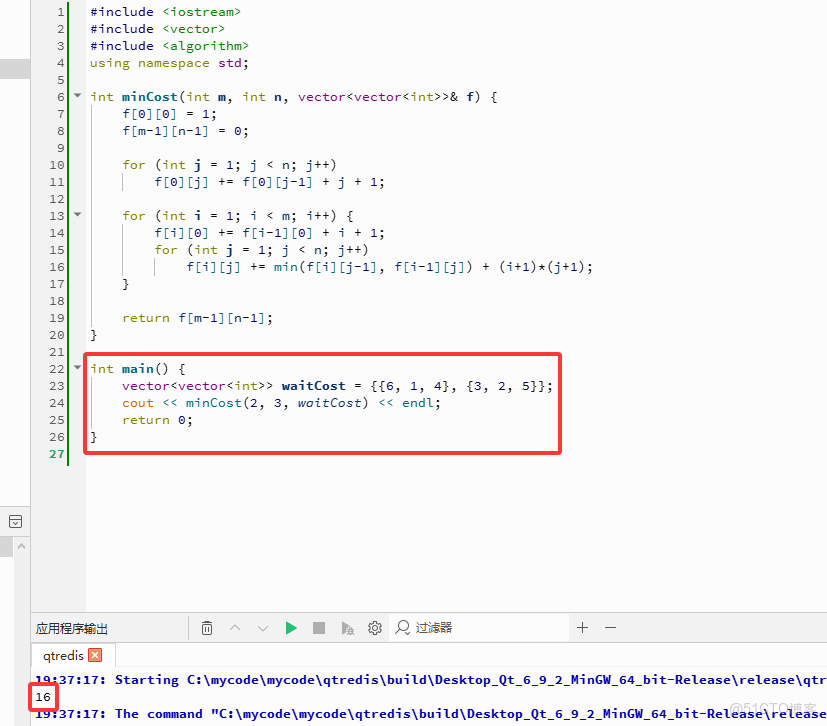
C++完整代碼如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int minCost(int m, int n, vector<vector<int>>& f) {
f[0][0] = 1;
f[m-1][n-1] = 0;
for (int j = 1; j < n; j++)
f[0][j] += f[0][j-1] + j + 1;
for (int i = 1; i < m; i++) {
f[i][0] += f[i-1][0] + i + 1;
for (int j = 1; j < n; j++)
f[i][j] += min(f[i][j-1], f[i-1][j]) + (i+1)*(j+1);
}
return f[m-1][n-1];
}
int main() {
vector<vector<int>> waitCost = {{6, 1, 4}, {3, 2, 5}};
cout << minCost(2, 3, waitCost) << endl;
return 0;
}