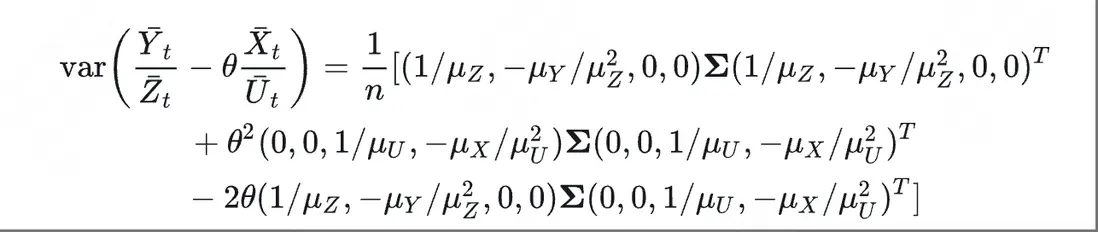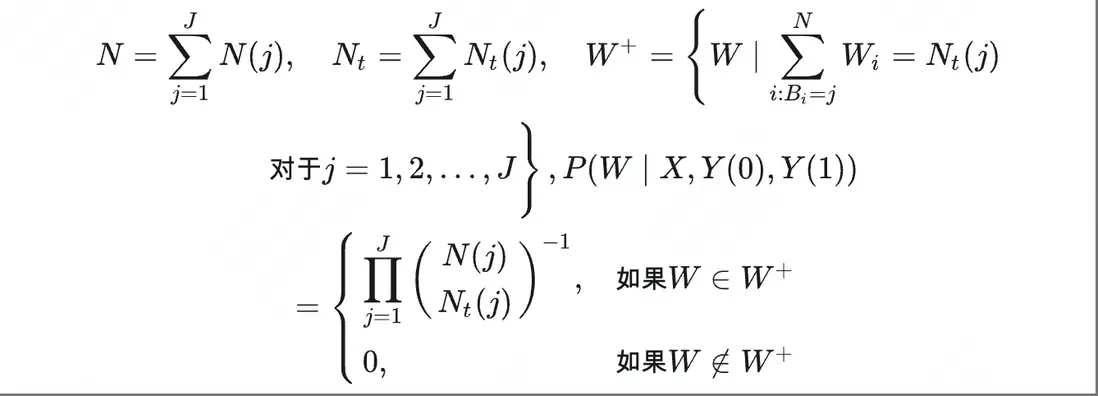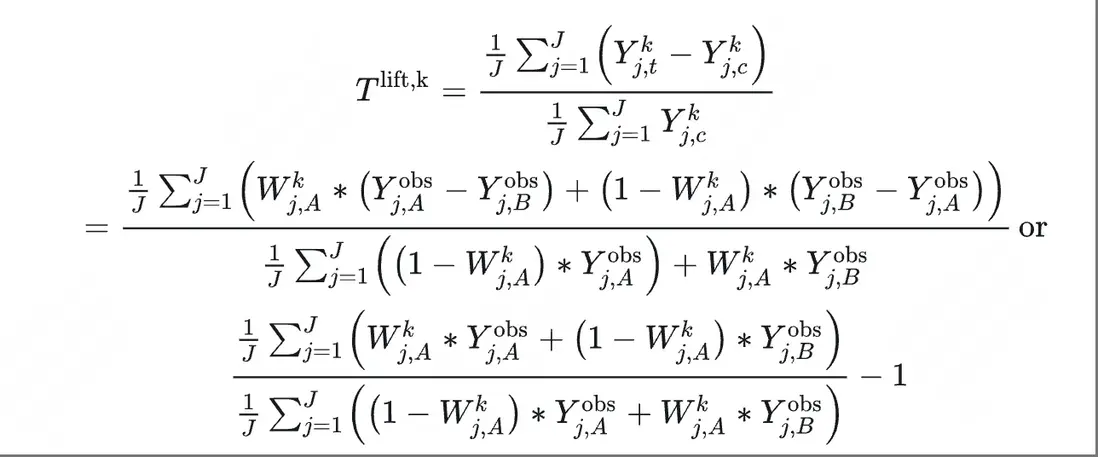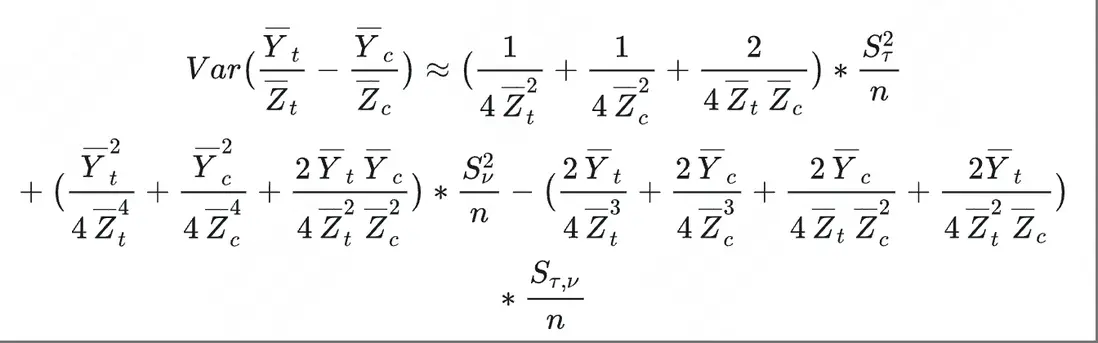本文系《可信實驗白皮書》系列的第三篇文章，第一篇文章我們介紹了為什麼要寫AB實驗白皮書，第二篇文章講解了AB實驗的理論原理及其背後的統計學基礎。本篇我們將重點介紹隨機對照實驗相關的一些基礎知識，以及提高實驗功效的一些常見方法。

備註：本篇排版為圖文混合排版，如果想獲得更好的閲讀體驗，建議訪問「美團技術團隊」知乎官方賬號《可信實驗白皮書系列03：隨機對照實驗》。

在美團到家業務場景中，經常會碰到隨機分流的實驗場景，比如全城AOI（Area of Interest，可以是小區、學校等點位，是按照社會功能定位，在地圖上將特定區域繪製成一個個電子圍欄的面狀地理信息）隨機分流或者訂單隨機分流。在隨機對照實驗中，我們可以定量判斷A、B兩個策略是否有顯著的差異，如果有差異則進一步探究哪個更有效，並依次對更優的策略進行推廣。因此，隨機對照實驗是幫助業務和算法探索並迭代策略的重要工具。

3.1 經典隨機對照實驗

隨機對照實驗是AB實驗最基礎且最重要的實驗方式。對於施加實驗策略的對象，理想情況下，我們想要在完全相同的時間與外部環境下將其與不施加實驗策略的對象進行對比。但是我們沒有穿梭時空的超能力去直接觀測另一個平行時空中這些對象的表現。而隨機對照實驗就是連通現實與平行世界的一個橋樑，使得我們可以人為模擬出平行世界中的情形。

另一個重要假設是個體處理穩定性假設，即SUTVA假設（Stable Unit Treatment Value Assumption）。它要求實驗單位的表現是獨立的，且干預效果穩定，實驗單元的行為結果不受到其他單元分組的影響，不會因為實驗組和對照組的關聯而產生干擾或者溢出。

3.1.1 隨機對照實驗的限制與挑戰

隨機化分組能使所有可能的混雜變量（包括未觀測到的混雜變量）在實驗組和對照組之間呈均勻分佈，消除混雜變量帶來的影響，提升結果可信度。因此，只要實驗條件允許，隨機對照實驗就是我們的首選選擇。在理想情況下，同一個個體在兩個平行時空完全一樣。但現實生活往往不如人所願，在有限的樣本量下，隨機分出的兩部分對象會存在一定差異，也即可交換性無法嚴格滿足。此時，我們需要一些定量標準來刻畫兩組之間的差異是否可以被忽略，即同質性檢驗。在隨機對照實驗中，我們會選取一段實驗前週期，對實驗組和對照組兩組的需要考察的一些指標值進行差異是否顯著的檢驗。當兩組結果沒有檢驗出顯著差異時，我們可以認為同質性檢驗通過，也即可交換性近似滿足，此時使用隨機對照實驗得到的結果是可信的。

儘管隨機對照實驗的可信性最高，我們也常常會面臨很多客觀上的限制與挑戰：

1. 公平性：在一些特殊業務場景，考慮到對用户以及騎手等羣體的公平性，無法對考察羣體進行隨機分組
2. 溢出效應：實驗單元之間存在相互影響與干擾，造成結果偏差。例如，在調度算法等場景，分別在實驗組和對照組的兩個區域往往會召回相同的騎手，即存在實驗組和對照組兩組之間的相互干擾。
3. 小樣本量情形：美團履約業務中有很多通過地理單元分流的隨機對照實驗。對於使用配送城市、配送區域、配送站點等面積較大單元的實驗，在可用流量有限的情況下，樣本量一般較少（幾十個甚至十幾個）且地域差異明顯，分組難以保證同質且難以檢測出顯著的策略提升效果。
4. 業務影響：在諸多業務場景會考量留對照組對實際業務影響的情況。如果對照組流量過多，可能存在影響當前線上策略效率的風險，從而對體驗指標造成影響，造成用户端客訴。為了不影響正常業務，一些場景的實驗組比對照組會採用95:5等極端的分組比例，實驗功效較低難以檢測出顯著的策略提升。
5. 流量未全部觸發策略：在履約業務中，存在很多圈選流量與實際策略觸發流量不完全一致的情況。為了準確評估策略效果，我們應該考察實際被策略觸發的流量。此時的同質性需要進一步重新驗證。

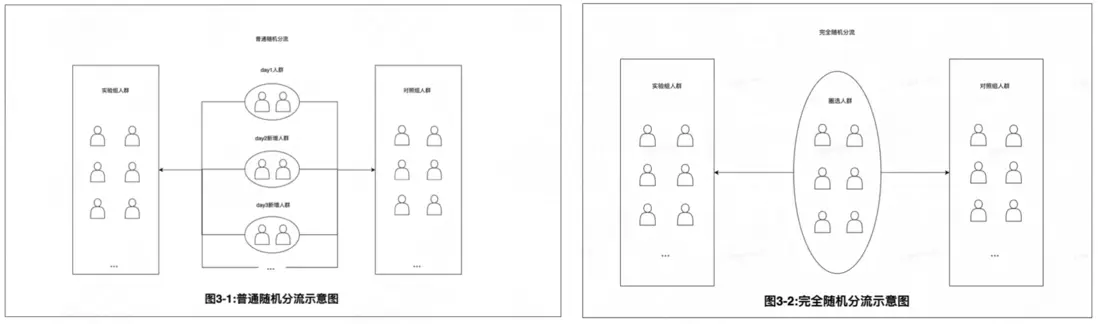
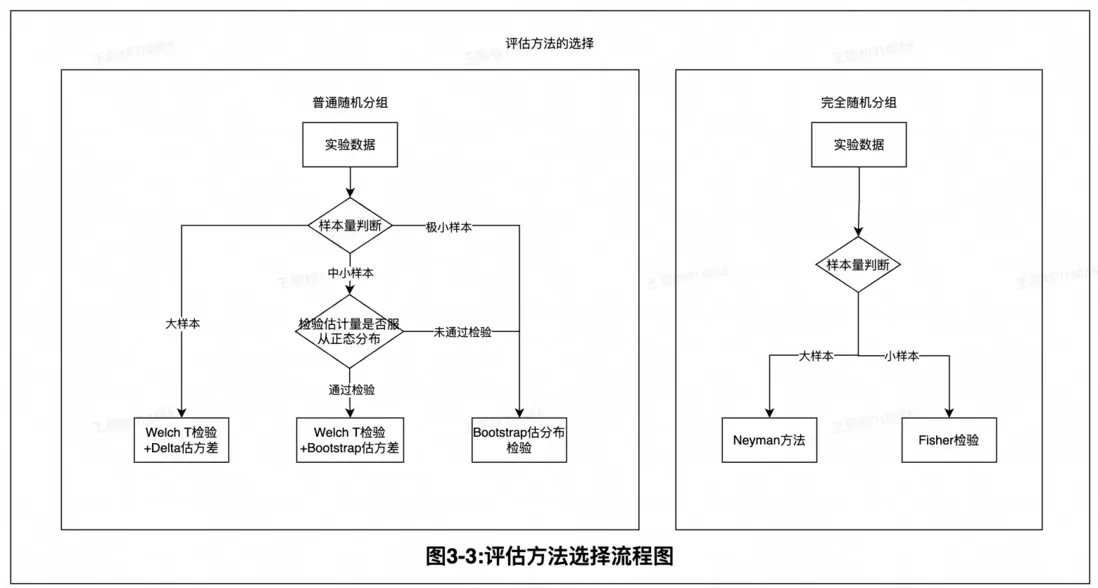
在美團的實驗應用中，經典的隨機對照實驗通過普通隨機分組和完全隨機分組兩種方式來實現，並相應配套有同質性檢驗和顯著性檢驗的評估方式。通常來説，我們會取實驗前一段週期的實驗組和對照組兩組指標表現，來進行同質性檢驗以驗證分組特徵的均衡性，也即近似保證隨機對照實驗的可交換性。而在實驗完成後，我們會取實驗期間的指標數據進行顯著性檢驗，來判斷策略效果是否顯著有效。同質性檢驗和顯著性檢驗實際上使用的都是下面同一套流程與方法，區別在於：我們希望同質性檢驗結果不顯著，則可以認為兩組表現相似，而希望顯著性結果顯著，則可以認為策略有效。本文主要詳細討論兩組的情況，多組情況下相應的分組與評估方式可以類似推廣，這裏不再過多地進行闡述。

3.1.2 普通隨機分組

正交的AB實驗，需要保證流量足夠的均勻分散，這就需要一個性能高、效果好的Hash算法來支撐，這裏我們選用了MurmurHash3_32。

1.分組機制

2.適用場景

• 實驗單位之間相互獨立；
• 尤其適用於樣本量較大，隨着實驗不斷進行，可能有新的實驗單位不斷進入實驗的場景。比如訂單分流、用户分流、AOI分流等實驗場景。

3.評估方式

（1）連續型指標

Delta方法

Bootstrap方法

（2）比率型指標

Delta方法

Bootstrap方法

3.1.3 完全隨機分組

由於互聯網很多涉及訂單的實驗有幾十萬以上的海量數據，這種大樣本情況下會廣泛使用哈希函數來進行普通隨機分組。而在美團的履約配送業務當中，常常會涉及人羣分流以及配送城市、區域、站點等地理單元的分流，圈選出的樣本量相對較少。例如，人羣分流涉及的樣本量較少時在1000左右，且由於業務約束一般只能允許留有較少的對照組，會採用相對極端的分流比例（例如95:5）。此時如果採用普通隨機分組方式，一定概率會出現1000人的分組中對照組只有30～40人的情況，實際會較大影響實驗的檢驗功效。同樣的，對於較大面積的地理單元分流，通常樣本量在100以下，即使採用5:5分流，也可能出現分組較不均勻的情況。因此，在這種情況下，我們會採用完全隨機分組的方式，以事先嚴格保證最終分組的比例與實驗設定的比例一致，使實驗符合預期設定。

1.分組機制

2.適用場景

• 實驗單位之間相互獨立；
• 適用於實驗前能夠確定全部進入實驗的實驗單元的場景；
• 對於小樣本的實驗推薦採用，以確保分組比例與實驗功效，尤其是分組比例不均衡的情形。

3.評估方式

評估方式與完全隨機輪轉的實驗方式相同，都可以通過Fisher方法和Neyman方法來計算，其中Fisher對小樣本情形的顯著性計算更為準確但計算成本相對高，Neyman方法在大樣本情形中計算更為便捷。具體方法原理可以參見第四章隨機輪轉實驗。

3.1.4 評估中的統計陷阱

在實驗的評估中，常用的顯著性計算公式並不是放之四海而皆準的，需要結合實際場景與使用方式精細判斷。實驗者需要關注一些潛在的統計陷阱，防止得出錯誤的顯著性結果：

1. 分配機制陷阱：忽視樣本在實驗組或對照組的分配機制，可能會導致方差計算的錯誤。例如業務上有時由於產品限制，會採用對流量id奇偶分流進行實驗，這時實際上沒有任何隨機性，且與其他隨機實驗的流量不正交，容易影響其他進行隨機分流實驗的結果。又例如一些業務方可能會對實驗單位進行分層分組以確保各層表現相似，又或者通過多次分組來使兩組指標差異小於一定的閾值。這時實際上已經對分流的隨機性進行了限制，使用常規公式進行顯著性計算時會高估方差。在本章後續3.3節中會討論分層隨機分組相關內容，在3.5中會提及重隨機化的顯著性計算方式。
2. 計算口徑陷阱：不同的指標類型，比如連續型指標、比率型指標、求和型指標，或者不同的指標差值口徑，比如計算絕對差值、相對差值或者ROI差值，其顯著性計算的方式都有所不同。如果忽視這些差異，可能會導致方差計算的錯誤。
3. 檢驗方法陷阱：對於不同的樣本量和數據分佈特性，應該選用合理的分析方法。當樣本量比較大時，我們根據中心極限定理可以認為數據的均值近似服從正態分佈，從而可以使用Delta方法評估；而當樣本量很小或者數據分佈離正態分佈差異較大時，此時使用Delta方法評估可能會導致方差估計不準，我們需要採用更為穩健的非參數檢驗方式，如Bootstrap估分佈等方式。
4. 多重比較陷阱：當指標個數較多時或者有多個實驗組時，此時會涉及同時進行多組假設檢驗。單個假設檢驗可以控制第一類錯誤為$\alpha$，而多個假設檢驗中至少一個被錯誤拒絕的概率卻是大於$\alpha$的。因此如果不考慮使用多重比較對$p$值進行修正，可能出現假陽性，影響對策略結果的判斷。在第七章的高階工具中我們會詳細論述多重比較的用法。
5. 獨立性陷阱：分析單位與分流單位的不同，可能會帶來錯誤的方差計算。通常來説能使用隨機對照實驗的情況中，分流單位之間是獨立的，但更細的分析單位無法保證獨立性，例如分流單位是用户，但我們期望分析每個用户下的訂單，這時訂單之間相互並不是獨立的。我們在方差計算時需要注重單位之間的獨立性。

3.1.5 特殊指標類型的評估方式

1.求和型指標

在一些特殊的實驗場景中，會存在無法圈選或定義實際受策略影響的實驗單位，只能獲取產生事實的實驗單位，因此如果使用常規的均值計算方式是不合理的。例如假設在一些uuid隨機分流實驗中，我們只能取到下單用户的數據，實驗組策略使部分不會下單的用户下了少量單，只取下單數據分析很可能導致實驗組單量均值降低，但單量的總和是增加的。對於連續型指標的這種情況，我們採用求和計算來評估是更加符合常理的。與均值計算相比，主要差異體現在相對提升以及方差的計算上。

Delta方法

Bootstrap方法

2.ROI型差值

在履約涉及花費的業務中，除了考慮常規的指標提升，還需要考察效率。從指標定義上來説，所針對的指標本質也是比率型指標，但計算的不是絕對差值，即實驗組分子/實驗組分母-對照組分子/對照組分母，而是計算ROI型差值，即：

3.1.6 隨機對照實驗配套功能

1.驗證樣本量均衡的SRM檢驗

驗證實驗中的樣本分佈是否與預期一致的檢驗，被稱為SRM（Sample Ratio Mismatch）檢驗。如果SRM檢驗不通過，那麼除非我們能夠診斷SRM的原因在哪裏，否則結果是不可信的。因為SRM檢驗不通過時，可能由於一些潛在原因導致分組的隨機性被破壞，從而違反隨機對照實驗的基本假設。SRM的成因多種多樣，原因大致可分為五類：

1. 實驗分配階段，例如流量未正確分桶、隨機分組方法有問題等；
2. 策略實質性階段，例如各組的准入條件發生了變化、數據傳遞丟失等；
3. 數據處理階段，例如沒有對未發生事實的單位補零等；
4. 實驗分析階段，例如使用了錯誤的分析時間週期，使用了錯誤的過濾條件；
5. 其他干預手段，例如遭受黑客攻擊。

2.MDE與最小樣本量計算

實驗在當前條件下能有效檢測的指標差異幅度即為MDE。在實驗報告分析階段計算MDE來判斷不顯著的指標結論是否是由於樣本量不足所導致，避免實驗在靈敏度不足的情況下得到非顯著結論，而做出認為策略沒有效果的誤判。

具體的雙邊假設檢驗下MDE的計算公式如下：

3.2 提高實驗功效的辦法

在線上AB實驗中，常常會出現實驗功效不足而檢測不出顯著性的情況。一種最常用的方式是增加樣本量來提高實驗功效，但這會增大實驗成本。另一種提高檢測靈敏度的方式是創建一個方差更小並能捕捉相同信息的評估指標。方差縮減的方式有很多，例如CUPED、分層分析、迴歸調整、配對實驗等。在這節我們主要介紹CUPED（Controlled Experiment Using Pre-Experiment Data）在履約和外賣實驗中的一些應用，在下節中我們會討論分層隨機分組和配對隨機分組。在履約和外賣的實驗場景中，CUPED能夠降低50%左右的策略效果估計量方差，大大提升檢驗靈敏度並減少實驗所需樣本量。

3.2.1 CUPED降方差原理

我們可以總結出，CUPED降方差主要有以下的適用條件：

1. 有實驗前可用的數據：例如用户、地理單元等實驗單位，都有較長週期的實驗前歷史數據可用。對於訂單等在實驗中新產生的實驗單元，沒有歷史數據可用，使用CUPED意義不大。
2. 指標數據表現穩定：由上述的CUPED降方差思想可以看出，當使用的協變量（一般是實驗前的指標數據）與實驗數據相關性很高時，降方差效果越好。因此，當指標數據相對穩定，不會隨時間變化或者開展實驗而出現劇烈波動時，會呈現實驗後數據與實驗前數據有較好相關性的情況，從而能更多降低方差，提升實驗功效。
3. 選取的協變量對於實驗組和對照組期望一致：當協變量受到干預變量影響的時候，此時導出的CUPED估計量不再是策略效果提升的無偏估計，可能存在偏差。因此實驗前的指標值作為天然的滿足不受干預影響的協變量，常常是CUPED協變量的首選。

3.2.2 連續型指標和比率型指標CUPED方法的應用

在業務中會遇到很多比率型指標的評估，這時我們無法直接使用經典的CUPED降方差方法。我們在常規CUPED方法的基礎上，進一步建立了比率型指標的降方差方式。對於比率型指標，我們探索瞭如下三種基於迴歸調整的CUPED降方差的方法，其中二元迴歸係數調整CUPED方法和新CUPED方法都通過嚴格證明可以降低比率型指標的方差。

1.一元迴歸係數調整CUPED方法

2.二元迴歸係數調整Cuped方法

3.新CUPED方法

與前面部分對比率型指標的分子分母分別進行降方差操作不同的是，新CUPED方法直接對比率型指標整體進行降方差。核心思想參考了Deng et al. (2013)對於用户隨機流時實驗單元和分析單元不一致的情況，將其拓展到一般比率型指標上的應用。具體構造的無偏估計量如下：

再使用Delta方法分別計算兩項的方差，以實驗組為例，有：

3.3 進一步保證同質性的實驗方式

同質性檢驗是一種用於確保在實驗前通過隨機分流後，實驗組和對照組之間沒有顯著差異的手段。如果同質性檢驗未通過，則意味着在實驗開始前，兩組之間存在系統性差異。通常，對於那些在實驗前後高度相關的指標來説，如果在實驗前未能達到同質性，這些指標在實驗後也可能表現出系統性差異，從而影響實驗結論的準確性，無法真實反映策略效果。

隨機對照實驗是AB實驗中最基本且可信度最高的方式，在樣本量充足的情況下，能夠有效平衡兩組之間的協變量分佈，從而通過同質性檢驗。然而，在特定的實驗條件和業務需求下，簡單的隨機分流可能仍然無法完全滿足實驗需求。例如，在樣本量較小的情況下（如幾百甚至幾十），單次隨機分流難以輕鬆獲得同質的分組，即使同質，組間差異可能仍然較大。

此外，業務上不僅關注實驗組和對照組的整體同質性，還常常進一步關注按某些重要特徵分層後的同質性，並對各層進行深入分析以獲得精細化的實驗結果。在有限樣本量下，簡單隨機分流往往難以同時保證各層的同質性，尤其是在分層較多的情況下。對於一些不可預測和不可控的因素，我們也無法通過實驗前的同質性驗證來確保兩組在實驗期間的這些因素相似，而策略的觸發條件或使用效果往往依賴於這些特殊因素。為了應對樣本量有限、分層分析以及不可控因素等挑戰，我們探索並制定了一些更加精細化的分組策略，以進一步保證同質性，從而提高實驗的科學性和結果的可信度。在實際業務場景中，我們已經積累了分層隨機分組、配對隨機分組、協變量自適應分組等方法，以進一步確保同質性。接下來，我們將逐一介紹這些方法的原理和適用場景。

3.3.1 分層隨機分組

在美團的實驗場景中，分層隨機分組被廣泛應用於驗證不同分層的運營策略的效果。通過這種方法，我們可以根據特定特徵進行分層，在每一層進行完全隨機分組，確保層內樣本在主要特徵上具有相似分佈以滿足同質性，從而減少潛在的混雜因素對每一層實驗結果的影響，便於探查策略在不同層的效果，進行精細化分析。此外分層隨機分組在數學上實際等價於CUPED中將協變量設置為分層協變量的示性函數的情形，在層間差異顯著時能夠有效降低方差，提高實驗功效。分層抽樣的核心思想是將總體樣本根據分層協變量情況（如年齡、性別、城市規模等）分為若干獨立的層，然後在每層內分別進行隨機分組，並聚合各層結果以獲得最終估計。以下是關於分層隨機分組的一些應用經驗與建議。

1.優點

• 提高同質性：通過在層內隨機化，保證了實驗組和對照組在分層變量上的相似性，從而提高了實驗的同質性。
• 減少偏差：進一步有效控制潛在的混雜變量，尤其減少了分層協變量對實驗結果的影響。
• 提高統計功效：由於減少了組間差異，分層隨機分組通常能夠提高統計分析的功效。

2.侷限性

• 分層變量選擇的挑戰：選擇合適的分層變量需要深入瞭解研究對象，使得分層後各層羣體差異明顯，且不當選擇可能導致分層效果不明顯或過多。
• 層數和樣本量的限制：分層過多可能導致每層樣本量偏少，影響統計分析的有效性，尤其在樣本總量有限時。
• 實施複雜性：分層隨機分組增加了實驗設計和實施的複雜性。當分層層數很多時，大規模的實現通常費時費力，並且會帶來分組表達式繁冗等缺點。

3.適用場景

使用分層隨機分組實驗設計需要滿足以下條件：

• 獨立性：實驗組和對照組必須是相互獨立的，分層結果與實驗策略的實施相互獨立。
• 存在分層差異：實驗單元在某個協變量上有較為明顯的差異。
• 樣本量要求：每一層下的實驗組和對照組樣本量應滿足最小樣本量要求，如果層內人數過少，缺乏某一組，則需重新劃分層。

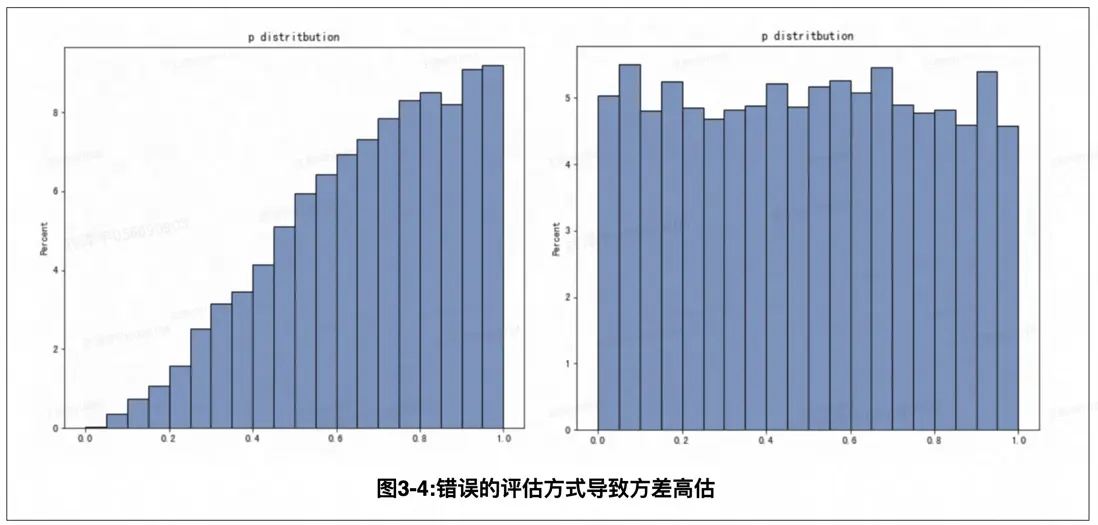
分層隨機分組是一種有效的實驗設計方法，旨在通過控制層內同質性和層間異質性來進一步保證同質性，提高實驗結果的準確性和統計功效。需要注意的是，分組機制應當與評估方式對應，分層分組的實驗設計在評估時採取分層評估分析。一個常見的誤區是採用分層隨機分組卻採用常規的隨機對照評估方式，這樣會導致顯著性計算錯誤。如下圖左邊是使用分層隨機但採用完全隨機的方式進行評估，會較為嚴重的高估方差，AA模擬中p值不再服從均勻分佈，實驗功效降低（但能控制第一類錯誤），而右邊是使用分層評估方式，AA模擬中$p$值表現為正常的均勻分佈。

在每一層使用隨機對照實驗評估方式的基礎上，我們可以採用Neyman方法計算每一層的指標差異和方差，並使用統合分析工具進行加權，從而獲得整體效果的評估。這種方法也能夠有效支持比率型指標的分層隨機分組實驗設計與評估。以下是其基本原理和實現過程。

1.分組機制

2.評估方式

Neyman方法計算方差與$p$值

3.3.2 配對隨機分組

配對隨機分組是指通過將實驗對象根據某些關鍵特徵進行配對，每對中的一個對象被隨機分配到實驗組，另一個則進入對照組，以確保實驗組和對照組在這些特徵上的均衡性。此方法通過控制個體間的差異來進一步保證同質性，提高實驗功效，特別適用於樣本間存在顯著異質性的研究。當樣本量較少時，或者實驗策略的觸發因素不可控，受到外部環境因素（如地理位置、時間段等）影響時，配對可以儘可能控制實驗組和對照組的外部環境因素相似，也能夠保證其他關注特徵儘可能同質，減少這些因素對於實驗結論的影響。以下是關於配對隨機分組的應用經驗。

1.優點

配對隨機分組的實驗方式在許多方面表現出色，但也可能有一些侷限性。我們詳細總結了其優缺點，首先其優點很明顯：

• 控制個體差異，進一步保證同質性：通過配對相似的個體，配對隨機分組能夠有效控制個體差異，進一步保證實驗組、對照組的同質性，提高實驗結果的可信度。
• 提高統計功效：在樣本量有限的情況下，配對可以提高統計功效，使得實驗更容易觀察到顯著效果。
• 應對小樣本量：在樣本量較小的情況下，配對隨機分組仍能有效地平衡組間特徵。

2.侷限性

• 配對複雜性：找到合適的配對對象可能需要額外的時間和資源，尤其在樣本特徵複雜或數量龐大時。
• 樣本利用率降低：如果無法為某些對象找到合適的配對，這些對象可能無法被納入實驗，導致樣本利用率降低。

3.適用場景

• 個體差異顯著的場景：當實驗對象之間存在顯著的個體差異時，配對隨機分組有助於控制這些差異，保證同質性。
• 樣本量有限的場景：在樣本量較小的研究中，配對可以提高實驗的統計功效。
• 外部環境影響大的場景：在實驗結果可能受到外部因素（如地域差異）顯著影響的情況下，配對有助於提高結果的內部有效性。
• 複雜多因素干擾的場景：當涉及多個干擾因素時，配對可以通過對這些因素的匹配來提高實驗設計的複雜性和精確性。

下面主要介紹配對隨機分組的基本原理。

1.分組機制

2.評估方式

（2）比率型指標評估

從業務理解出發往往需要考慮比率型指標，例如實驗組GMV完成率定義為 （實驗組所有區域完成GMV）/（實驗組所有區域GMV）, 而不是實驗組每個區域GMV完成率的平均值。針對配對隨機分組實驗下比率型指標評估的理論研究幾乎沒有，在此探討部分我們通過AA模擬來保證方法的科學性。

Fisher方法

Neyman方法

在美團履約側的實驗場景中，許多策略（如調度優化等）的作用單元為區域粒度等較大的地理單元，且策略的觸發因素受到外部環境的影響。這意味着無法保證觸發策略的實驗組、對照組區域的外部環境相似，這使實驗設計面臨很多獨特的挑戰，特別是在確保實驗組和對照組的同質性方面。

1.實驗粒度限制：由於一些策略的最小作用單元是區域，這限制了實驗無法在更細粒度上（如訂單）分流。而城市下的區域數量較少且策略的觸發因素受到外部環境的影響時，隨機分組難以保證觸發策略的實驗組、對照組同質。

2.其他影響因素：區域內的交通狀況、訂單密度等因素也可能在實驗期間發生變化，進一步增加了實驗組和對照組之間的異質性。

3.3.3 協變量自適應分組

在美團履約側的實驗場景下，調度等場景下樣本量稀少與地域差異明顯的現狀使得隨機對照實驗下難以保證分組的同質性以及很難有效地檢測出實驗提升效果。受自身業務形態和空間維度限制，調度等算法的最小作用單元為區域，且通常情況下以區域組作為策略施加的單位，受限於策略的最小作用單元，在實驗設計上只能考慮區域或區域組維度的分流，這就導致參與實驗的樣本量較少，在這樣的中小樣本場景下（樣本量幾十到幾百），協變量自適應分組可以通過減小組間指標分佈不平衡性，使得分組更同質，從而有效提升點估計的準確度，在保證同質性和提升統計功效等方面普遍優於經典的隨機對照實驗分組。

協變量自適應分組（Covariate-Adaptive Randomization）是一種在實驗設計中用來進一步保證同質性的實驗方式，旨在通過減小實驗組和對照組之間重要協變量分佈的不平衡性，使得分組更同質，來提高實驗結果的準確性和可靠性。在隨機對照試驗中，協變量自適應分組通過序貫分配的方式，使得各組之間在關鍵協變量上的分佈更加相似，減少了協變量對試驗結果的混雜影響。下面是一些協變量自適應分組的應用經驗。

1.優勢

協變量自適應分組的優點在於它能：

• 進一步保證同質性：通過平衡重要協變量，進一步保證了實驗組對照組的同質性，使得分組更同質。
• 提高統計功效：平衡協變量後，由於減少了組間差異，協變量自適應分組通常能夠提高統計分析的功效。
• 適用於小樣本：在小樣本場景下（如幾十到幾百個樣本），協變量自適應分組能夠顯著提升同質性和估計精度。

2.侷限性

• 計算成本增加：相比於經典隨機對照實驗的分組方式，協變量自適應分組需要更多的計算時間。
• 需要先驗知識：需要對重要協變量有較好的理解和認知能力，以選擇合適的協變量進行平衡。

3.適用場景

• 個體差異顯著的場景：在實驗對象之間存在顯著個體差異的情況下（如區域間地理差異等），協變量自適應分組可以有效平衡這些差異。通過在實驗組和對照組之間平衡重要協變量，確保個體差異不會顯著影響實驗結果的解讀。
• 樣本量有限的場景：在樣本量較小的研究中，協變量自適應分組有助於提高實驗的統計功效。小樣本量可能導致組間協變量的不平衡，協變量自適應分組通過動態調整分組策略，確保在小樣本條件下，實驗組和對照組的協變量分佈儘可能相似，從而提高結果的可靠性。

平衡協變量對於實施可靠A/B實驗是極為重要的，可以有效地降低處理效應估計的偏差，而協變量自適應設計則是為實現這一目標最為常用的方法。在協變量自適應隨機化過程中，往往以每一步最小化某特定的不平衡測度為目標，序貫地（Sequential）將實驗個體逐個（或逐對）分為試驗組和對照組，其中不平衡測度的選擇包括但不限於協變量均值（Covariate Means）、馬氏距離（Mahalanobis Distance）、離散化加權處理、核方法等。以下是其基本原理和實現過程。

1.不平衡測度的刻畫標準

在這裏之所以考慮馬氏距離 (Mahalanobis Distance) 來定義不平衡度 Imb，是基於以下幾點考量：

• 形式簡潔、計算成本低：馬氏距離的計算相對簡單，且符合統計學分析的直覺和業界常用評估指標的習慣。
• 不受數據線性變換的影響：協變量之間的量綱差異可能會對不平衡性的衡量過程帶來麻煩。馬氏距離不受數據線性變換的影響，省略了數據預處理的必要性，使得計算更加簡便和科學。
• 優良的統計學性質：馬氏距離具有減少估計處理效應方差的優良性質。在處理效應的估計中，馬氏距離能夠提供最優的漸進方差，使得實驗結果更加可靠。

2.協變量自適應分配方式

在進行協變量自適應分組時，學業界主要以完全序貫分配和配對序貫分配作為協變量自適應設計的分配方式。協變量自適應分配的主要思想是，逐個或者逐對分配實驗單元，其通過傾向於使不平衡測度差異最小來判斷將實驗單元分在實驗組還是對照組，在分組過程中動態調整以確保實驗組和對照組在關鍵協變量上的平衡。

(1)完全序貫分配

概率q通常選為0.85（也可0.75、0.9等等）。兩種分配流程各有優劣，完全序貫分配的隨機性更強，但很難保證分配到試驗組和對照組的樣本量相同，而配對序貫分配則可以用部分隨機性換取試驗組和對照組的樣本量相同的結果。

協變量自適應分組通過協變量回歸調整降低方差，在這個分組機制下的評估中，方差計算同經典隨機對照實驗中的CUPED方差削減技術，具體可參考經典隨機對照實驗部分，這裏不再贅述。

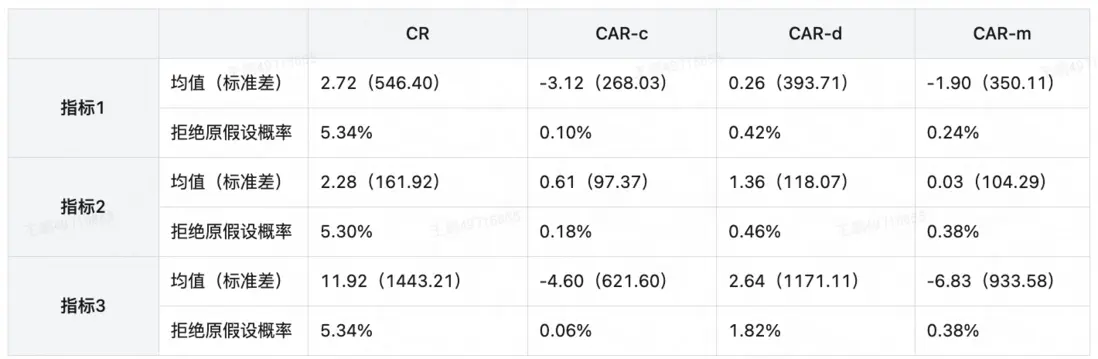
下面我們介紹一個使用協變量自適應分組得到更為同質區域分組的案例，我們比較了某業務場景中完全隨機分組和協變量自適應分組的多個指標情況。其中，CR代表完全隨機分組，CAR-c，CAR-d，CAR-m分別代表使用平衡均值，平衡離散型協變量，平衡馬氏距離的協變量自適應方法。表中結果顯示，在相同的檢驗顯著性水平為0.05下，協變量自適應設計下的各協變量的拒絕原假設概率更低，即更不易拒絕同質性檢驗，且能生成更為同質的分組，降低了分組後的組間差異均值和方差波動。

3.4 解決溢出效應難題的實驗方式

在AB實驗中，一個很重要的假設是SUTVA (Stable Unit Treatment Value Assumption，個體處理穩定性假設)，即實驗中每個實驗參與單元的行為是相互獨立的，然而實踐中由於實驗單元間的直接關聯或者間接關聯，參與AB實驗的實驗組與對照組之間可能並不獨立，我們通常稱這種實驗組、對照組間的相互干擾影響為溢出效應。

溢出效應的存在往往會引發實驗效果的估計偏差，進而損失實驗結論的可信度。例如通信工具Skype電話測試提升通話質量策略時，由於實驗組呼叫可以撥給實驗組或對照組的用户，從而對照組用户使用Skype電話頻率也會增加，因此實驗組和對照組之間的差值會被低估。溢出效應難題仍是目前學界與業界的重點研究領域，現有的實驗設計與解決方案主要有時間片輪轉實驗、聚類隨機試驗、雙邊實驗以及隨機飽和實驗等。其中時間片輪轉實驗在美團的實驗場景下已經落地應用，會在第四章中詳細介紹，這裏我們將分別重點介紹在美團履約側實驗場景下，如何通過區域溢入溢出效應模型以及隨機飽和實驗來解決溢出效應的問題。

3.4.1 區域溢入溢出效應模型

在美團履約的實際業務背景下，例如調度策略，由於混合調度下在分別在實驗組和對照組的相鄰區域可以召回相同騎手，導致實驗組與對照組之間共享騎手運力資源，使得實驗組和對照組區域單元的獨立性假設難以滿足。如何在總體效應中有效識別溢出效應，並將最為關心的直接效應分離出來，是互聯網企業在雙邊（多邊）市場背景下研究網絡因果推斷問題的關鍵技術難點。為此，我們通過與中國人民大學進行校企合作，引入了區域溢入溢出效應模型，在部分場景下解決了溢出效應問題。

在區域層面，我們建模刻畫了目標變量在不同區域間流動規模與方向，以及量化變動幅度，引入了“溢出權重”、“溢出強度”、“溢入權重”與“溢入強度”四大指標。其中“溢出權重”主要基於對目標變量在不同區域間流動規模與方向的考量，通過計算各區域間目標變量的流動量和方向，構建出反映流動規模與方向的綜合指標，直觀展示目標變量在區域間的流動情況，為決策提供參考。而“溢出強度”側重於衡量目標變量在某一區域內的變動幅度，通過計算某一時期內目標變量在該區域內的變化量，結合“溢出權重”，得出反映變動幅度的量化指標，幫助研究者與決策者快速識別變動幅度較大的區域，進行針對性分析與應對。同樣，“溢入權重”和“溢入強度”則反映與“溢出權重”和“溢出強度”相反方向的變動幅度。

區域溢入強度和區域溢出強度可以理解為周圍不同組別區域對自身的影響強度，最簡單的定義是周圍不同組別的區域個數比例（比如某單元自身為實驗組，周圍為對照組的比例越大，認為影響越強）。但是這種定義沒有考慮到周圍區域的大小及單量規模，一般認為大區域對自身的影響會比小區域對自身的影響強。因此，我們結合溢入（溢出）運單量來設計溢入（溢出）強度的定義。

溢入強度與溢出強度的現實意義：

參照下圖，在某次實驗中，對實驗組區域施加正向激勵的策略（如升級調度策略使實驗組區域單和騎手更匹配，實驗組單被騎手更好更快接起），則在全城運力和總訂單量無顯著變化的情況下，實驗組區域存量訂單快速被消耗，實驗組區域騎手傾向於跨區接起地理層面相鄰且沒有正向激勵策略的對照組的訂單。

3.4.2 隨機飽和實驗

隨機飽和實驗（Randomized Saturation Design）源於兩階段隨機實驗（Two-staged Randomized Experiment）的理念。與傳統的隨機對照實驗中僅有一個固定的實驗組與對照組比例不同，隨機飽和實驗通過將樣本劃分為多個簇，在每個簇中設置不同的實驗組與對照組比例。理論上，實驗組比例較高的簇對對照組的溢出效應更強，從而可以通過分析不同簇內實驗組、對照組的表現，檢測出真實的實驗效應和溢出效應。

隨機飽和實驗設計：

非參數模型建模

3.5 拓展與展望

在隨機對照實驗的業務應用中，觸發式分析具有重要作用。在某些特定業務場景中，實驗組可能並未全部受到實驗干預，導致直接比較實驗組和對照組的策略效果時，結果可能被稀釋，從而難以獲得顯著結論。這種情況通常是由於策略對全部實驗單元施加時，但僅一部分實驗單元被實際觸發策略，並且哪些單元被觸發通常由實驗單元選擇，實驗設計者並不可控。

在策略觸發的背景下，還會出現對照組的羣體可能“偷偷”受到策略干預，或者實驗組個體不遵守規則的場景，即依從者問題。如果感興趣測試藥物治療對某項疾病治療效果，隨機對照實驗考慮將病人隨機分為實驗組、對照組並且實驗組病人推薦藥物治療以及對照組不吃藥，實驗組病人有可能沒按要求吃藥，以及對照組病人有可能“偷偷”吃藥。此時可以採用CACE（Complier Average Causal Effect）估計與推斷來評估服從干預羣體的策略效果。

在降方差方面，CUPED 方法的協變量選取不僅限於實驗前的協變量。在實驗前不存在實驗單元或實驗前數據與實驗後數據相關性較差的情況下，也可考慮使用實驗中及實驗後的協變量進行調整。在 CUPED 方法的基礎上，學界和業界衍生出其他降方差的方法，如CUPAC、MLRATE、STATE等。

CUPAC和MLRATE都使用不受實驗干預影響的協變量特徵訓練機器學習模型，以預測目標評估指標，並將預測值作為迴歸調整中的協變量進行降方差。MLRATE在迴歸調整中加入了干預變量和機器學習預測變量的交互項，並使用交叉擬合減小過擬合帶來的偏差。STATE方法結合機器學習迴歸調整與$t$分佈，針對厚尾數據分佈進一步提升降方差效果。我們通過線下模擬和實際數據驗證發現，CUPAC和MLRATE能進一步減少約10%的方差，而STATE能降低接近50%的方差，但估計量會存在一定偏差。因此，在選擇降方差方法時，建議根據具體場景驗證後使用。

我們還嘗試了一些其他實驗方式以進一步保證同質性，未來也將考慮建設。重隨機化是一種實驗設計方法，用於在實驗分組之間實現更好的平衡，進而提高實驗的功效。重隨機化通過多次隨機分配實驗單元，直到在關鍵協變量上達到預設的平衡標準，例如實驗組和對照組的差異小於一定閾值或同質性檢驗中的$p$值大於一定閾值。這有助於確保實驗組和對照組在重要特徵上更加相似，從而減少混雜因素的影響。重隨機化可以從兩個方面提高實驗功效：

1. 改善組間平衡，降低實驗結果的方差，使得在相同樣本量下更容易檢測到真實效應；
2. 減少協變量不平衡，使實驗組和對照組在關鍵特徵上更相似，使結果更能反映策略的真實效果而非其他混雜因素。

在實踐中，需要事先定義需要平衡的協變量及可接受的分流程度。當對分流均衡性要求嚴苛時，可能需要多次隨機分流才能達到預期結果，增加了計算和時間成本。在實驗設計階段，應充分考慮這些因素，在結果準確性和計算成本之間找到最佳平衡，以確保實驗的科學性和可行性。確保實驗組和對照組的同質性是提高實驗結果可靠性和有效性的關鍵步驟，通過合理設計和實施減少混雜因素的影響，能使實驗結果更具可信度與推廣性。

對於實驗領域的溢出效應難題，我們當前主要考慮通過區域等地理單元以及訂單單元之間的溢出機制建模來解決。未來，我們將進一步探索使用馬爾科夫決策過程等方法解決無法物理隔離情況下分流溢出效應等難題。

參考資料

• [1] Deng et al. (2013)：Deng et al. (2013), Improving the sensitivity of online controlled experiments by utilizing pre-experiment data, In proceedings of the 24th International Conference on World Wide Web, ACM, 123-132.
• [2] Lin（2013）：Winston, Lin(2013), Agnostic notes on regression adjustments to experimental data:Reexamining Freedman’s critique, The Annals of Applied Statistics, 295-318.
• [3] Population Average Effect（PAE）：在整個目標人羣中某種處理或干預的平均效果。
• [4] 假設前提：假設每個個體實驗效果為常數，或者每個個體的實驗效果雖然不同但相對提升很小。（AA模擬情形下實驗效果均為0，假設成立）。
• [5] 部分假設：假設每個個體實驗效果為常數（AA模擬情形下實驗效果均為0，假設成立）。

閲讀更多

| 關注「美團技術團隊」微信公眾號，在公眾號菜單欄對話框回覆【2024 年貨】、【2023 年貨】、【2023 年貨】、【2022 年貨】、【2021 年貨】、【2020 年貨】、【2019 年貨】、【2018 年貨】、【2017 年貨】等關鍵詞，可查看美團技術團隊歷年技術文章合集。

| 本文系美團技術團隊出品，著作權歸屬美團。歡迎出於分享和交流等非商業目的轉載或使用本文內容，敬請註明 "內容轉載自美團技術團隊"。本文未經許可，不得進行商業性轉載或者使用。任何商用行為，請發送郵件至 tech@meituan.com 申請授權。