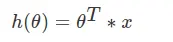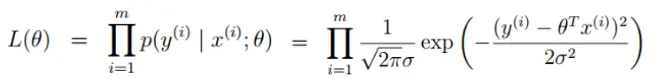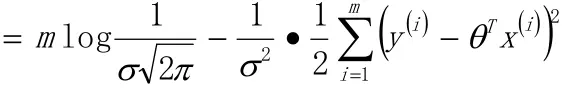1.線性迴歸算法思想
機器學習算法可以分為有監督學習和無監督學習。
什麼是有監督學習算法?
用已知某種或某些特性的樣本作為訓練集,以建立一個數學模型,再用已建立的模型來預測未知樣本,此種方法被稱為有監督學習,是最常用的一種機器學習方法。是從標籤化訓練數據集中推斷出模型的機器學習任務。
迴歸算法是有監督學習算法的一種,從機器學習的角度來講,迴歸算法用於構建一個算法模型,這個模型是屬性(X)與標籤(Y)之間的映射關係。
線性迴歸通過一個或者多個自變量與因變量之間之間進行建模的迴歸分析。
它的特點為一個或多個稱為迴歸係數的模型參數的線性組合。
2.線性迴歸示例
| 房屋面積(m^2) | 房租(元) |
|---|---|
| 10 | 800 |
| 15 5 | 1200 |
| 20 2 | 1600 |
| 35.0 | 2500 |
| 48 3 | 3300 |
| 58.9 | 3800 |
| 65.2 | 4500 |
將上面的數據看做一行樣本,我們可以得到如下關係
x(房屋面積) y(房租)
0 10 800
1 15.5 1200
...
5 65.2 4500如下圖
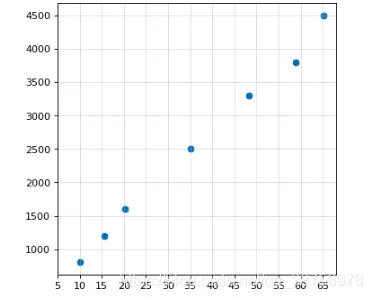
首先我們要找到這樣房屋面積與價格的映射關係, y=ka+b, 如下圖
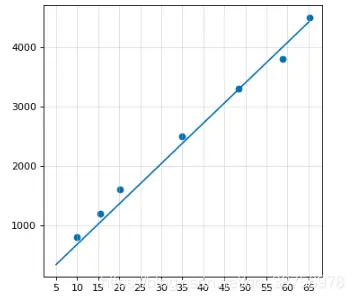
然後通過y=f(x)映射關係,預測房租價格。
這是一個特徵值的,那麼如果是兩個特徵值呢?我們找的就是一個平面。
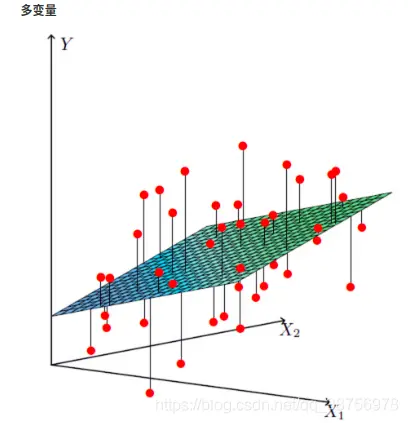
擴展到更多個特徵值,我們要找的映射關係就是
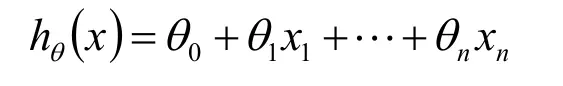
x就是特徵值,
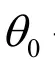
我們可以看做θ。* x。, x。為1,然後j得到這個式子
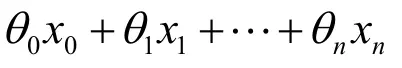
用向量來表示上面這個式子
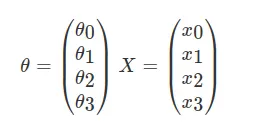
最終我們得到
3.誤差
我們得到這個模型,但顯然預測值與真實值存在誤差,用 ε來表示誤差。
對於每個樣本則有

由概率論的中心極限定理,可知誤差ε是獨立並且具有相同的分佈,並且服從均值為0方差為σ²的高斯分佈。
所以
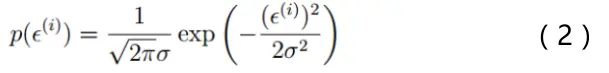
將(1)式帶入(2)式
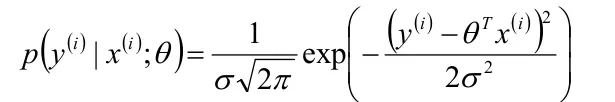
之後用到了似然函數:
為了便於求解,取對數
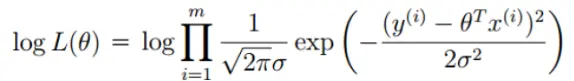
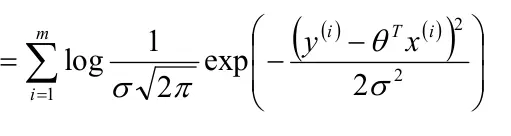
當
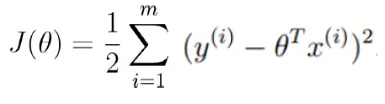
最小時, 也就是為0時, logL(θ)值最大,這個式子也就是我們的損失函數。
進一步變換:
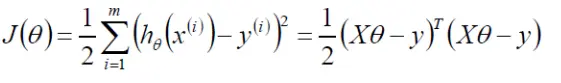
然後求它的偏導
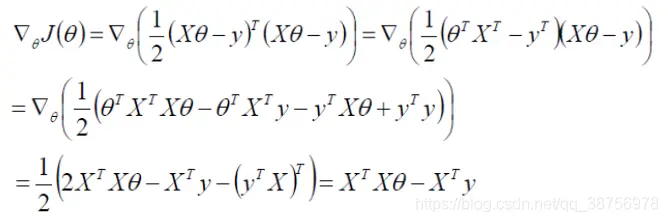
令偏導為0,最終可以求得
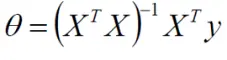
這個就是最小二乘法,也是線性迴歸損失函數的求解方法之一。
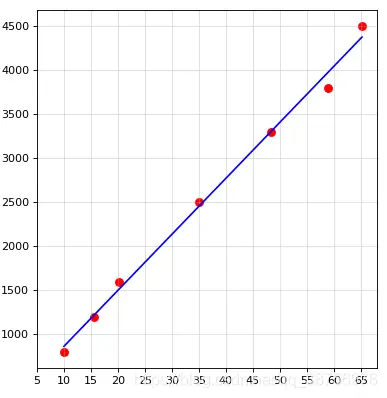
對於上面的房屋面積與房租關係樣本的代碼示例
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression as lr
# 房屋面積數據
x_list = [10, 15.5, 20.2, 35.0, 48.3, 58.9, 65.2]
# 對應的房租數據
y_list = [800, 1200, 1600, 2500, 3300, 3800, 4500]
x = np.array(x_list).reshape(-1,1)
y = np.array(y_list).reshape(-1,1)
model = lr()
model.fit(x, y)
y_plot = model.predict(x)
print(model.coef_)
plt.figure(figsize=(5,5),dpi=80, facecolor='w')
plt.scatter(x, y, color='red', linewidths=2,)
plt.plot(x, y_plot, color='blue',)
x_tick = list(range(5, 70, 5))
plt.grid(alpha=0.4)
plt.xticks(x_tick)
plt.show()
結果
[[63.66780288]]3.波士頓房價預測示例
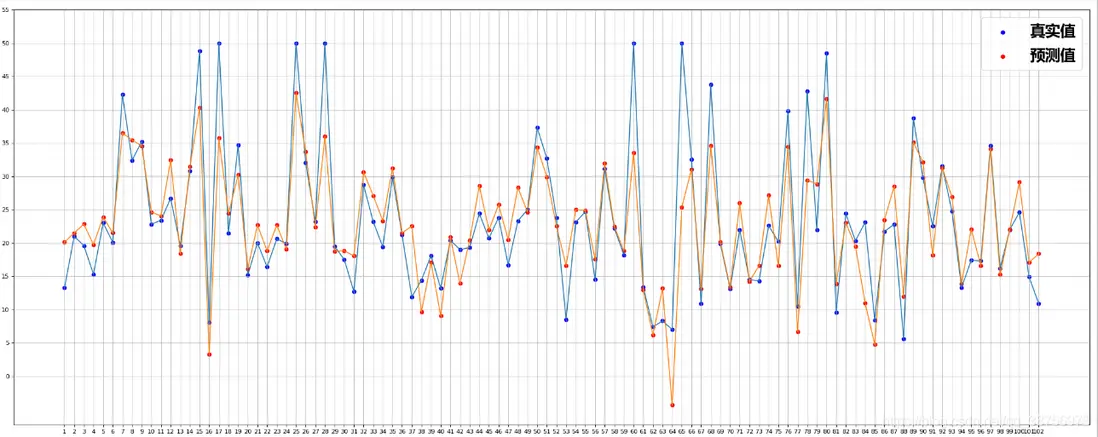
從sklearn.datasets中獲取相關數據集,使用標準線性迴歸,建立房價預測模型,並繪製房價預測值和真實房價的散點、折線圖。
代碼示例
# coding:utf-8
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression as lr
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from matplotlib import pyplot as plt
from matplotlib import font_manager
font = font_manager.FontProperties(fname="/usr/share/fonts/wps-office/msyhbd.ttf")
def my_predic_fun():
"""
使用線性迴歸預測波士頓預測房價
:return:
"""
lb = load_boston()
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.2)
x_std = StandardScaler()
y_std = StandardScaler()
x_train = x_std.fit_transform(x_train)
x_test = x_std.transform(x_test)
y_train = y_std.fit_transform(y_train.reshape(-1,1))
y_test = y_std.transform(y_test.reshape(-1,1))
model = lr()
model.fit(x_train, y_train)
y_predict = y_std.inverse_transform(model.predict(x_test))
return y_predict, y_std.inverse_transform(y_test)
def draw_fun(y_predict, y_test):
"""
繪製房價預測與真實值的散點和折線圖
:param y_predict:
:param y_test:
:return:
"""
x = range(1,len(y_predict)+1)
plt.figure(figsize=(20, 8), dpi=80)
plt.scatter(x, y_test, label="真實值",color='blue')
plt.scatter(x, y_predict,label='預測值', color='red')
plt.plot(x,y_test)
plt.plot(x,y_predict)
x_tick = list(x)
y_tick = list(range(0,60,5))
plt.legend(prop=font, loc='best')
plt.xticks(list(x), x_tick)
plt.yticks(y_tick)
plt.grid(alpha=0.4)
plt.show()
if __name__ == '__main__':
y_predict, y_test = my_predic_fun()
draw_fun(y_predict, y_test)結果
參考:https://blog.csdn.net/guoyunfei20/article/details/78053999