【JS逆向百例】某坤行 1101，雪球 1038，新 acw_sc__v2 逆向分析詳情 - 爬蟲 K哥爬蟲博客

聲明

本文章中所有內容僅供學習交流使用，不用於其他任何目的，不提供完整代碼，抓包內容、敏感網址、數據接口等均已做脱敏處理，嚴禁用於商業用途和非法用途，否則由此產生的一切後果均與作者無關！

本文章未經許可禁止轉載，禁止任何修改後二次傳播，擅自使用本文講解的技術而導致的任何意外，作者均不負責，若有侵權，請在公眾號【K哥爬蟲】聯繫作者立即刪除！

前言

最近有小夥伴博客留言，詢問關於雪球 1038 長串的相關逆向思路，該參數整體難度中等，有些細節地方會導致最後生成的參數無法使用，在瞭解長串之前先分析一下基礎的短串（某坤行），由簡到繁。非業務項目，本文僅對該參數進行逆向分析，僅供學習交流。

逆向目標

目標：某坤行/某雪球/acw_sc__v2
網址：
- aHR0cHM6Ly93d3cuemtoLmNvbS9pdGVtL0FBNjI0MjI5MS5odG1s
- aHR0cHM6Ly94dWVxaXUuY29tLw==
- aHR0cHM6Ly93d3cudGhmdW5kLmNvbS5jbi8=

抓包分析

某坤行

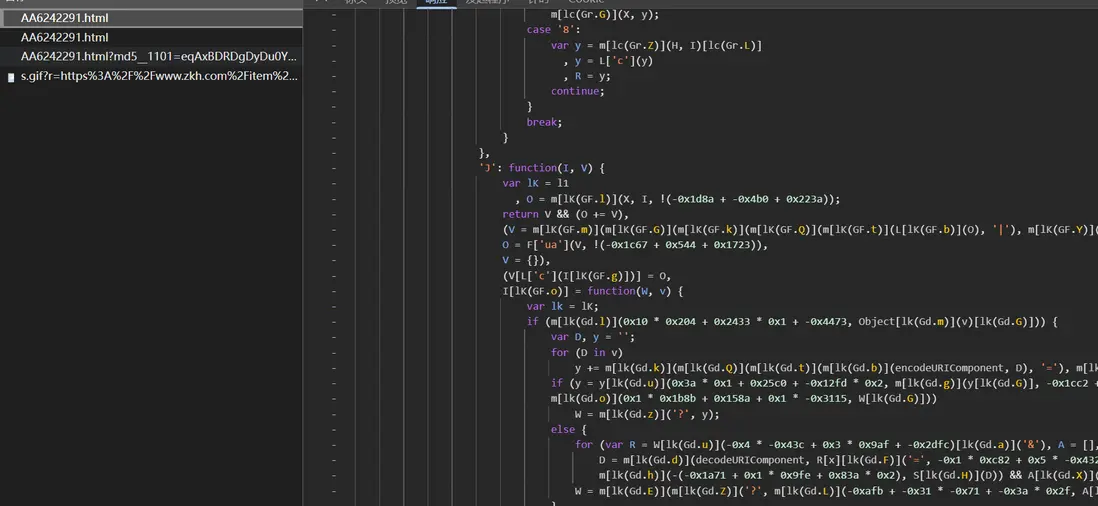
首先訪問詳情頁，發現他會請求 2 次，第一次返回帶混淆的 js 代碼：

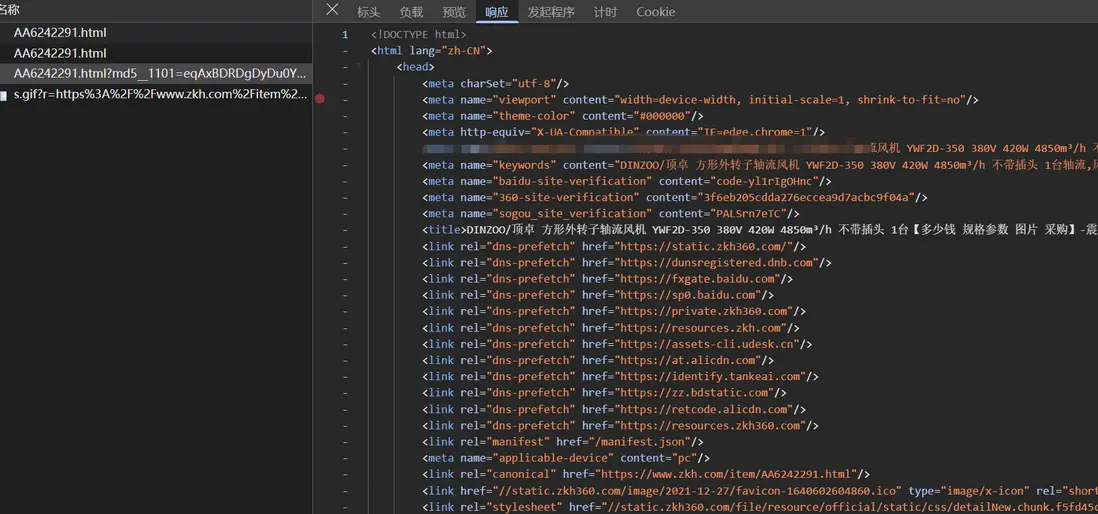
第二次請求，攜帶 md5__1101 參數即可返回正常的 html 內容：

某雪球

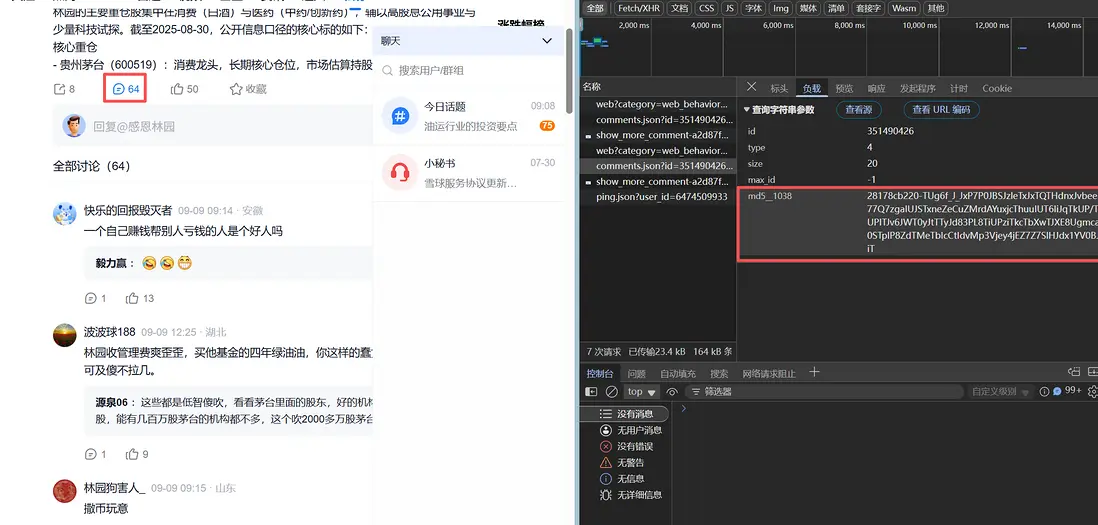
某雪球長串短串隨機觸發（大部分是長串），我們這裏點擊評論列表的小氣泡圖標，發起數據請求，其中載荷參數為主要分析對象：

本文由易到難，從短串到長串依次進行分析。

逆向分析

某坤行

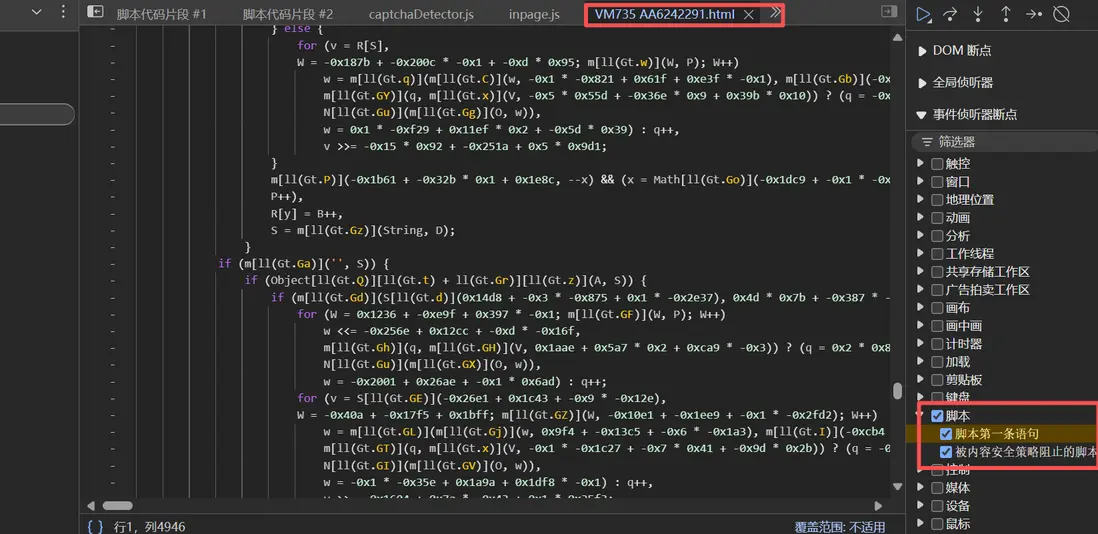
首先我們訪問詳情頁，下腳本斷點，發現他在 VMxxx.html 裏成功斷下，這裏發現 href 暫未生成相關參數：

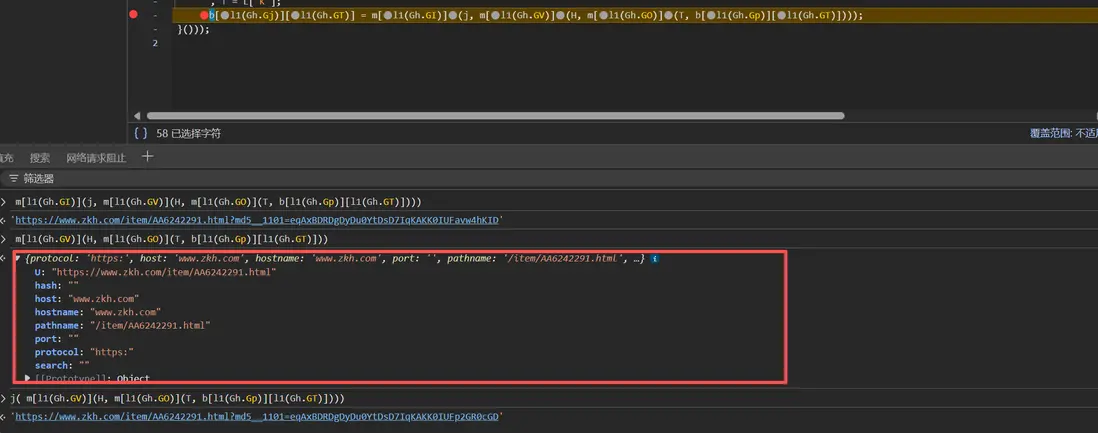
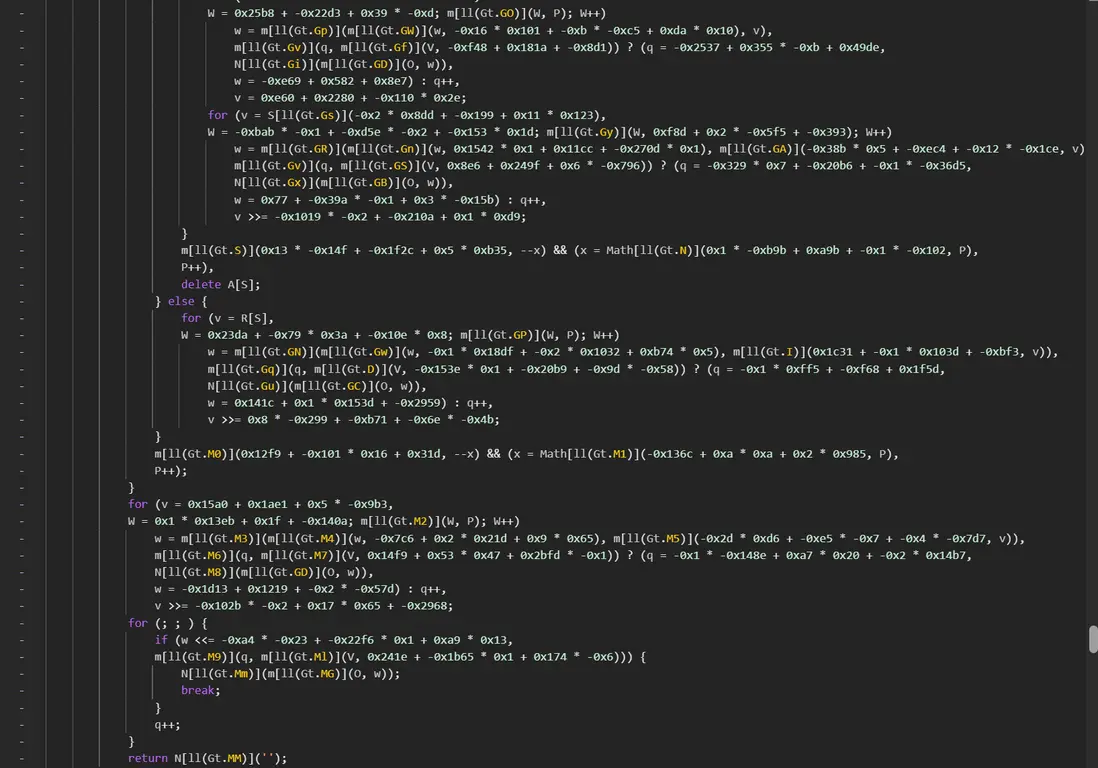
單步跟棧，最終發現在末尾調用 m[l1(Gh.GI)](j, m[l1(Gh.GV)](H, m[l1(Gh.GO)](T, b[l1(Gh.Gp)][l1(Gh.GT)]))) 方法，生成了新的 href 參數：

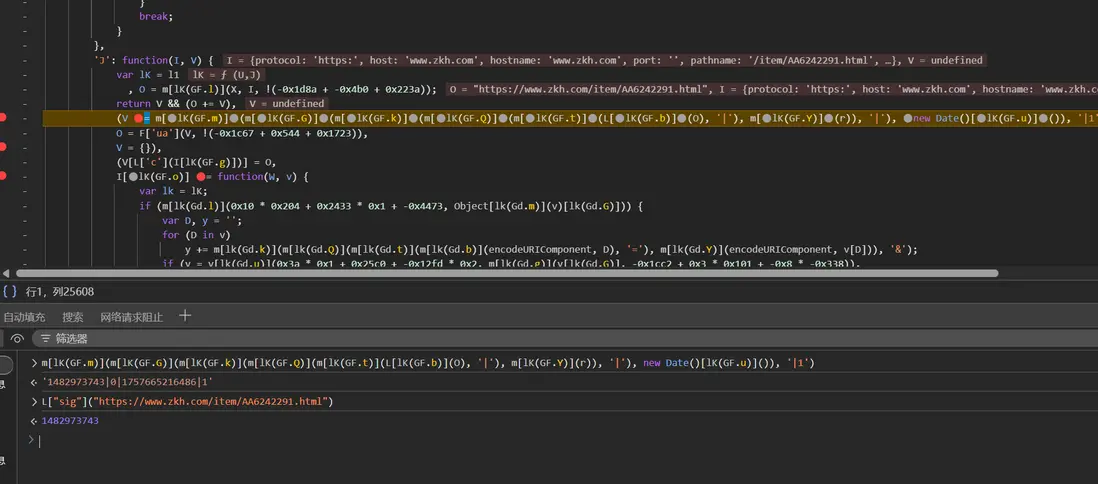
進入 j 函數，首先通過 sig 函數生成值後，再拼接時間戳等生成新參數，1482973743|0|1757665216486|1，將對應的 sig 算法扣下即可：

'sig': function(I) {
            var lU = l1;
            for (var V = -0x51b * -0x1 + 0x2051 * -0x1 + 0x1b36, O = m[lU(Go.l)](encodeURIComponent, I), W = 0x1 * 0x102d + -0x1 * -0x1b0f + 0x4 * -0xacf; m[lU(Go.m)](W, O[lU(Go.G)]); W++)
                V = m[lU(Go.k)](m[lU(Go.Q)](m[lU(Go.t)](m[lU(Go.b)](V, 0xa78 + -0x662 * 0x2 + 0x1 * 0x253), V), 0x1647 + -0x32e * 0x8 + 0x11 * 0x47), O[lU(Go.Y)](W)),
                V |= -0xfe1 * 0x2 + -0x1c9d + 0x3c5f;
            return V;
        }

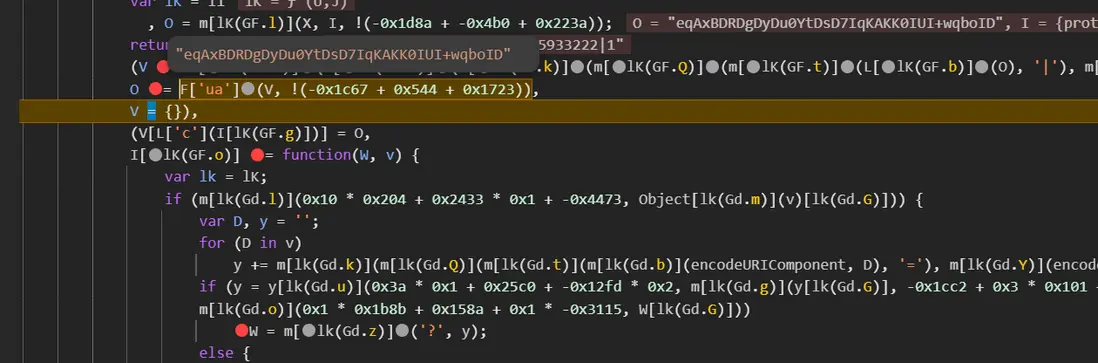
隨後將拼接好的參數經過 F['ua'](V, !(-0x1c67 + 0x544 + 0x1723)) 方法生成最終的參數：

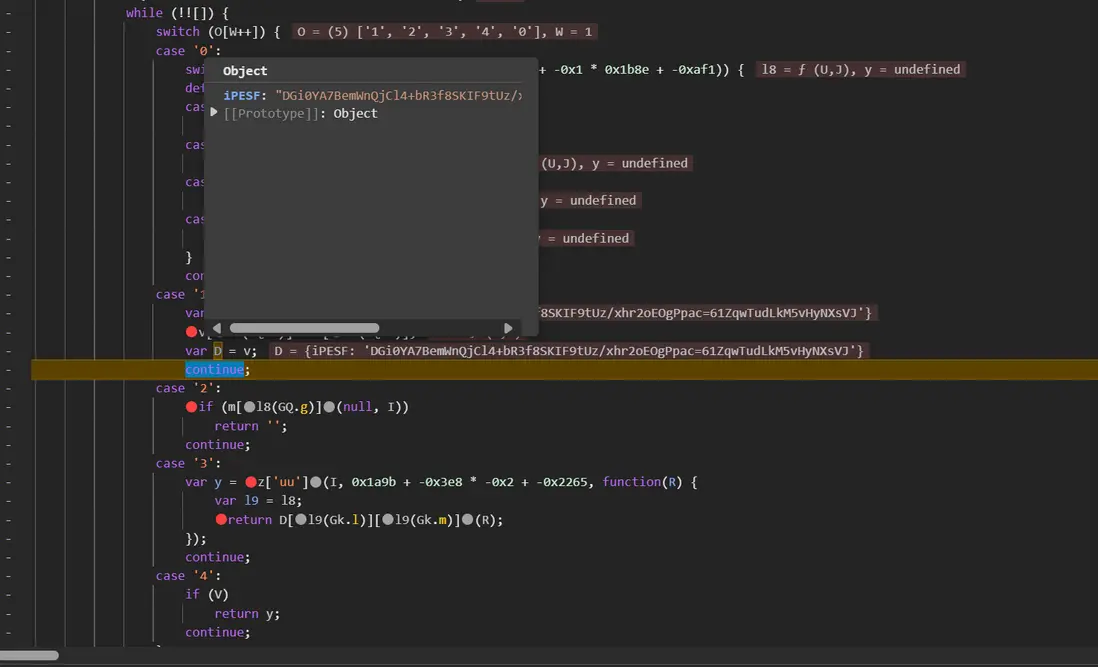
進入 ua 函數，是個平坦流，發現其主要生成邏輯為 uu，D 為固定值：

最終經過 z['uu'] 將 I 值與匿名函數傳入，生成 1101 值，只需將 uu 模塊整體扣下即可：

最後，攜帶正確的 1101 參數即可完成請求：

某雪球

無限 debugger

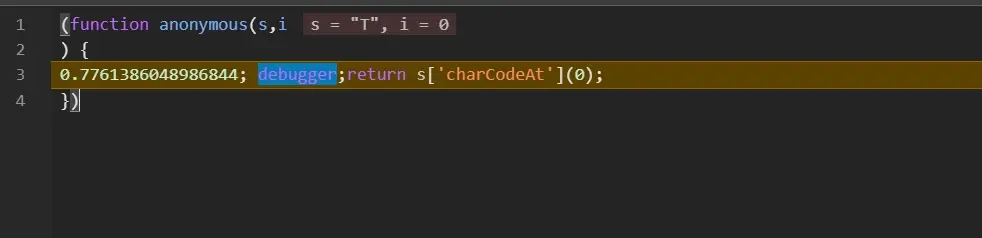
進入評論列表，打開 F12 觸發了無限 debugger，這個 debugger，之前也有粉絲問過，類型如下：

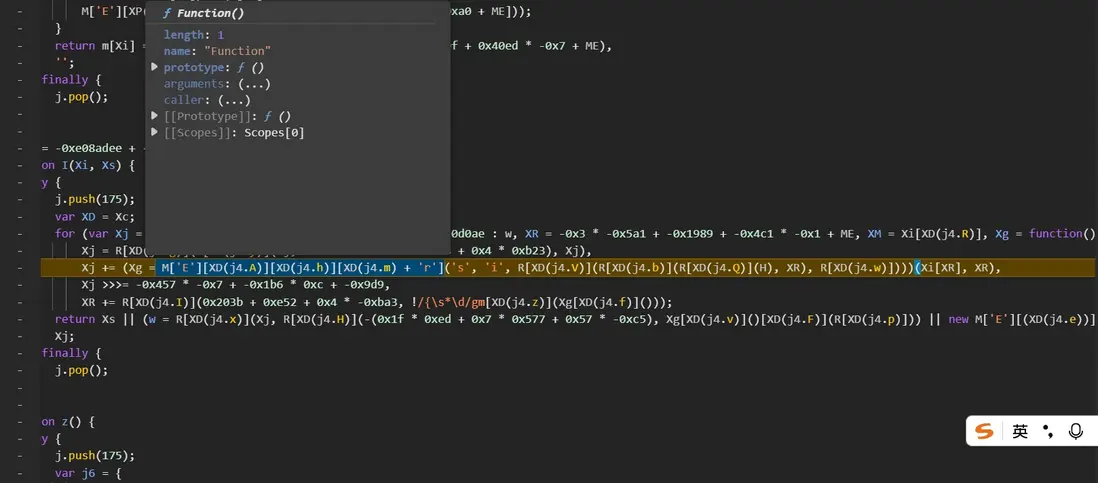
向上查看堆棧，發現是進入了大 Function，主要邏輯就是 s['charCodeAt'](0);，在其中插入 debugger 導致字符轉 Unicode 編碼時斷下：

將 js 修改為 (Xg = M['E'][XD(j4.A)][XD(j4.h)][XD(j4.m) + 'r']('s', 'i', R[XD(j4.V)](R[XD(j4.b)](R[XD(j4.Q)](H), XR), R[XD(j4.w)])),Xi[XR]["charCodeAt"](0)) 利用逗號表達式的特性將這個 debugger 過掉。

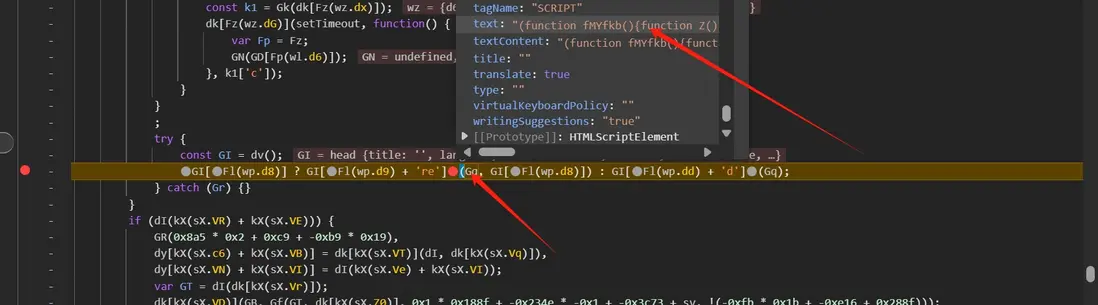
隨後我們就要找到這個 js 是在哪裏動態注入的，同 1101 參數思路一樣，下腳本斷點後刷新頁面，將我們修改後的 js 文本替換到 Gq.text 中：

再次刷新，發現 js 沒有觸發 debugger，但是瀏覽器卡死了，説明發現 js 被我們手動修改了。

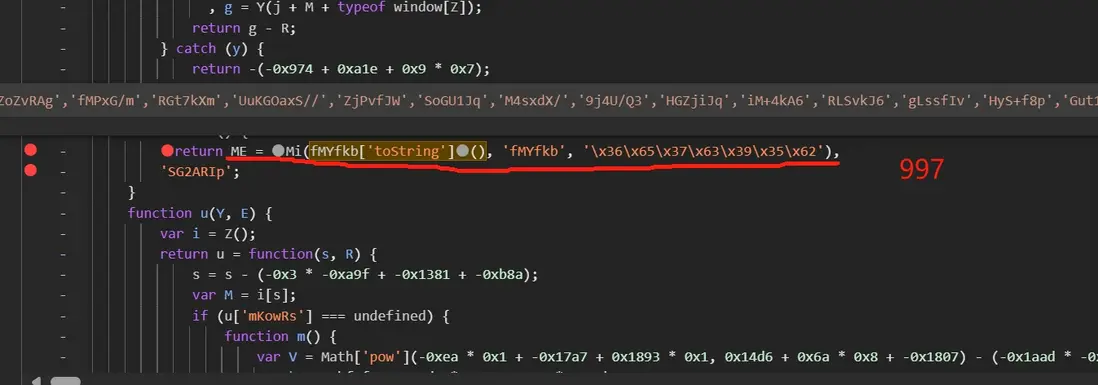
向上排查，可疑位置如下：

修改後會導致 js 發生改變，導致這裏 ME 不等於 997，我們將這裏也一併修改，讓 ME 恆等於 997，返回正常邏輯。再次替換，刷新頁面即可正常調試（首頁第一次請求 html 中 script 裏也會攜帶 js，同理替換，換湯不換藥，這裏不做區分。後續評論接口可按上述方法替換分析）。

這個屬於代碼執行過程中產生的 debugger，也可以直接用魔改瀏覽器過掉，可以參考：

瀏覽器魔改-從根本上通殺所有的無限debugger：https://mp.weixin.qq.com/s/up0frzR2Fl9ijtHikkfs7Q

逆向分析

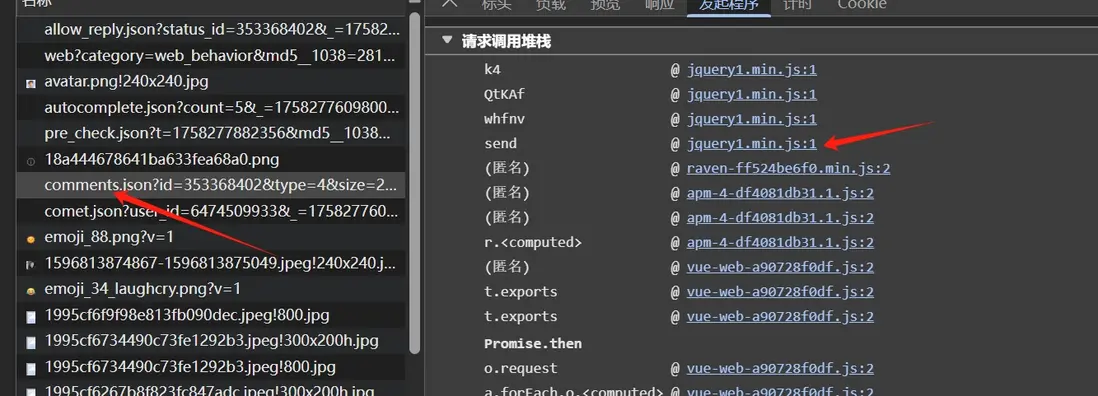
按抓包分析中的步驟，我們點擊評論按鈕，進入到下圖 send 堆棧處：

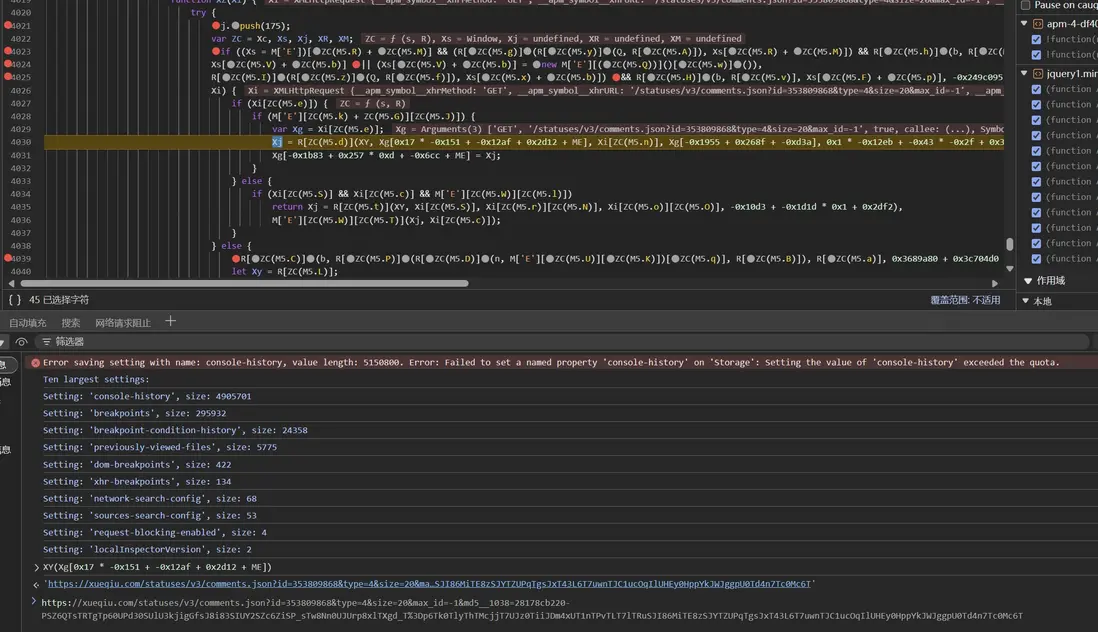
經過 GE 方法後，openArgs 中攜帶了 1038 參數，繼續跟進，發現進入到了類似 1101 參數的生成邏輯，但是比其更為複雜：

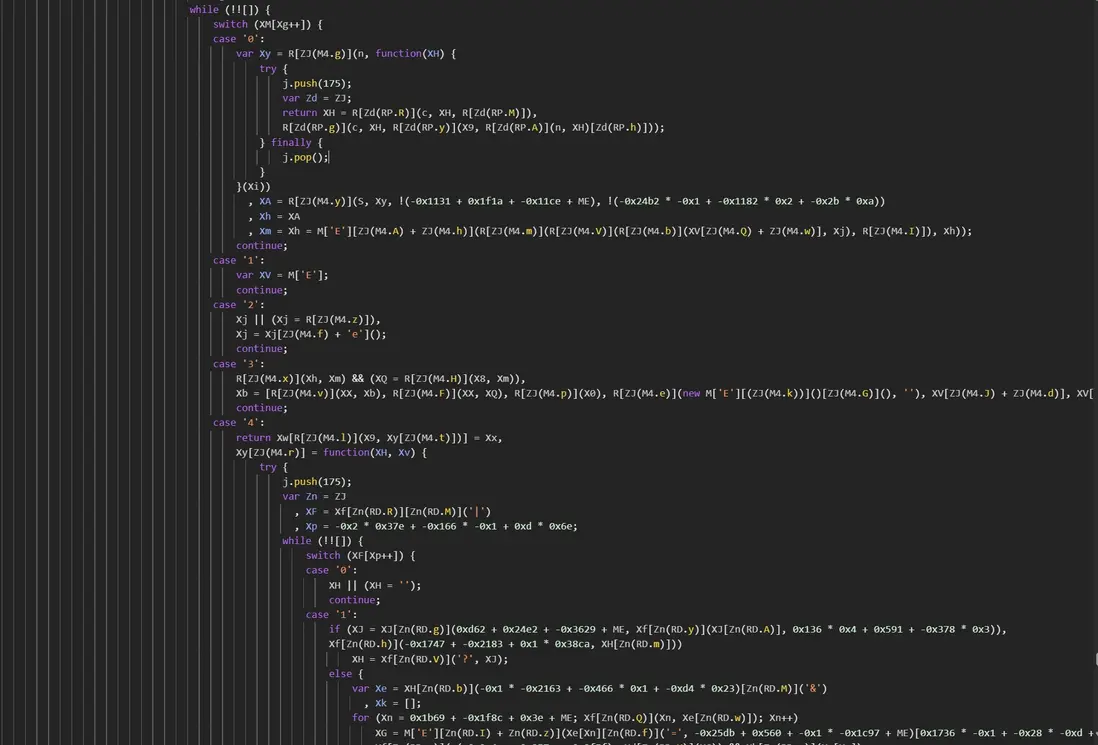
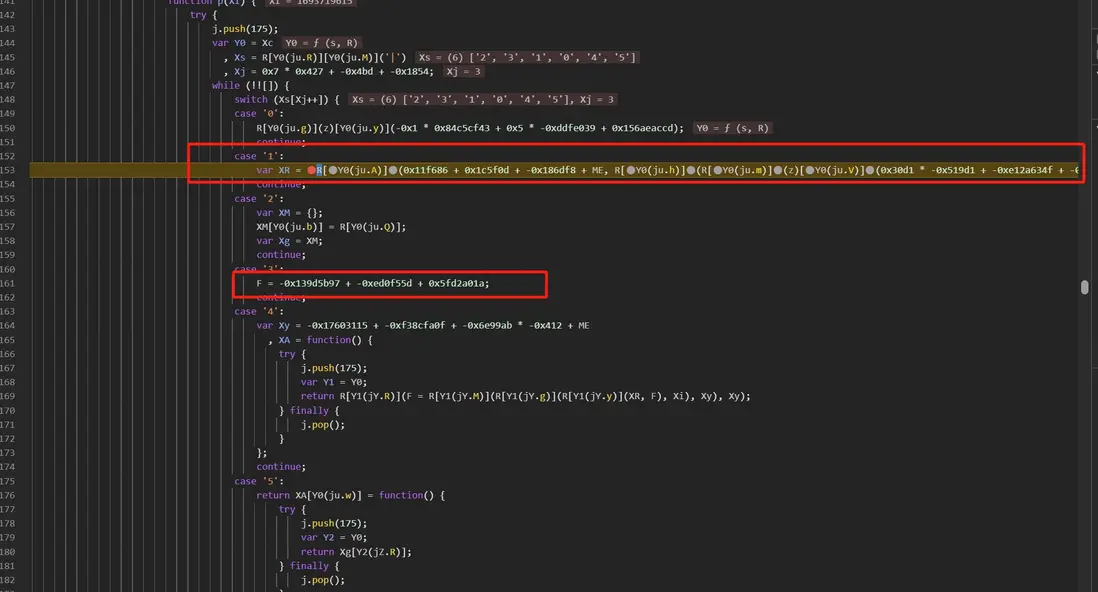
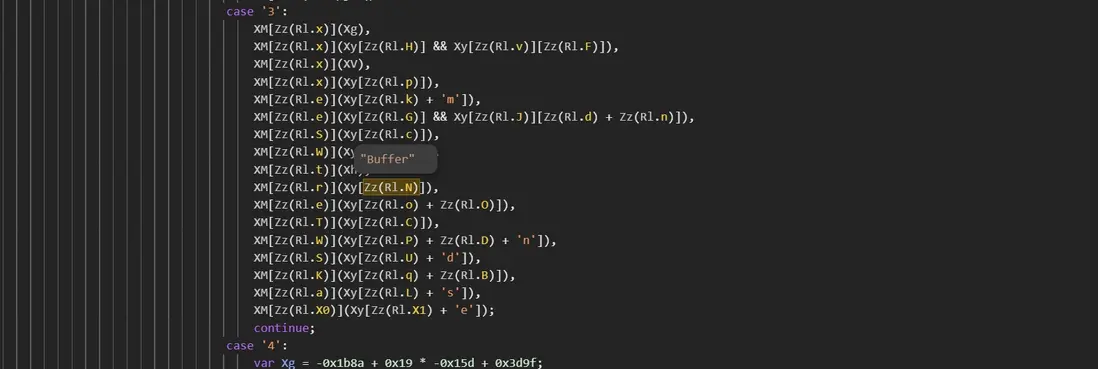
進入到加密函數 XY 中，發現是 switch 與 case 重重嵌套：

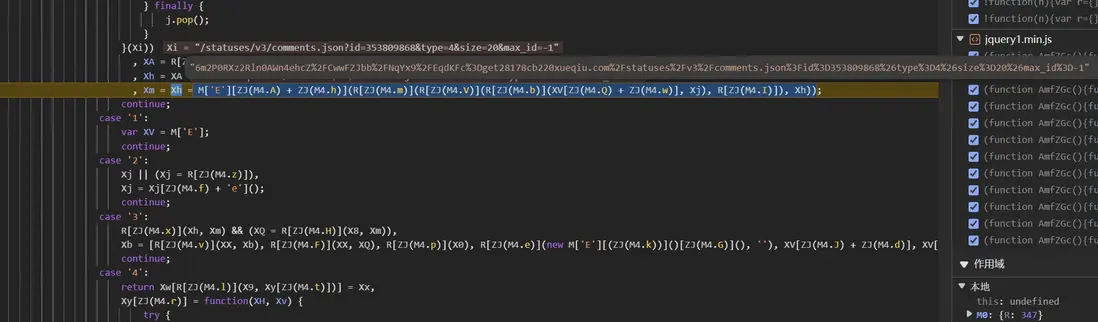
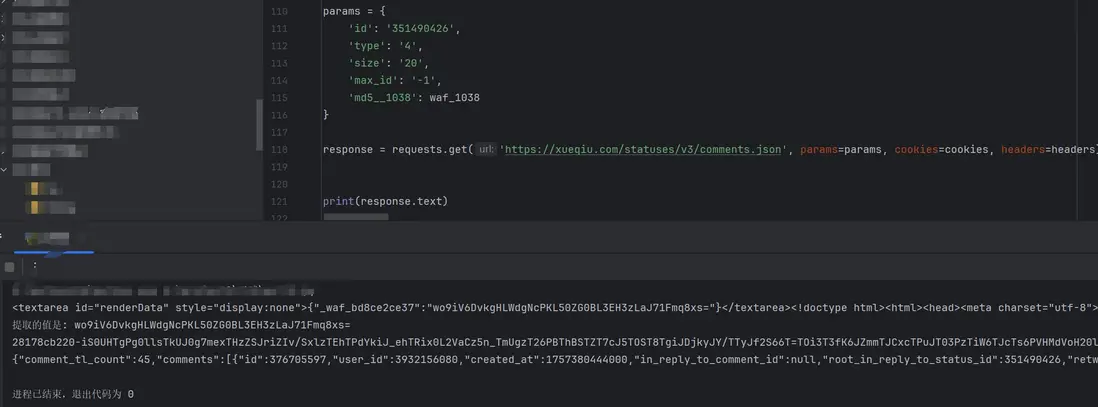
這裏不做解混淆，利用 1101 的思路去慢慢跟進，首先是對 params 進行了拼接然後編碼了一下：

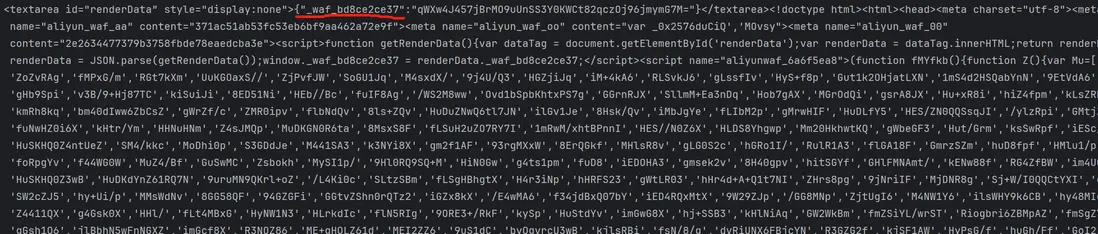
其中 _waf_bd8ce2ce37 是前置接口返回的：

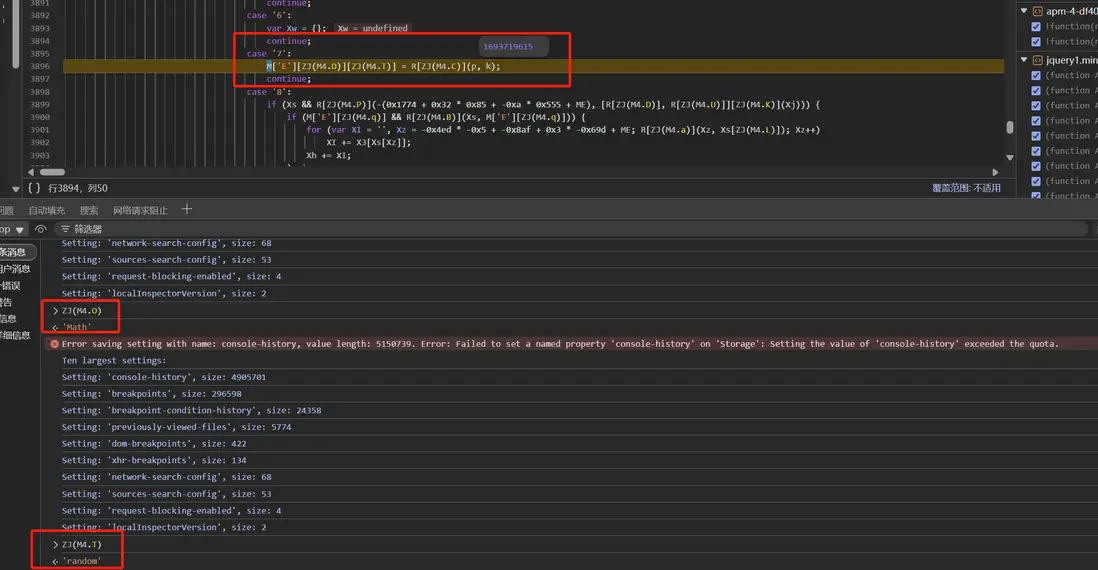
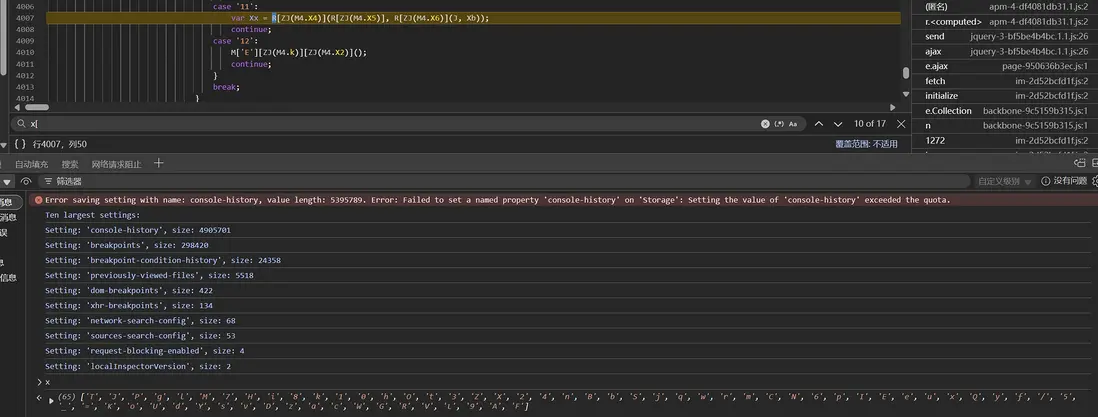
隨後繼續單步跟進，發現它魔改了 Math 函數：

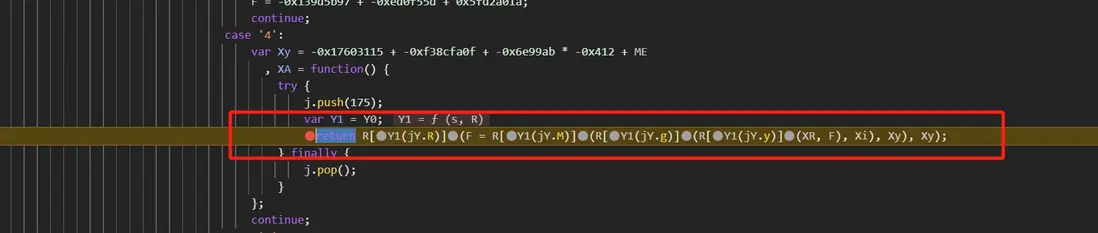
經過研究發現，類似固定隨機因子到自寫函數，使得 Math.random 可以得到自己想要的，進入 p 函數，發現每次置入隨機因子的時候，F 都會初始化一個值（這個可以用做觀察點，可以下斷點看看走完全程需要置入多少次隨機因子）：

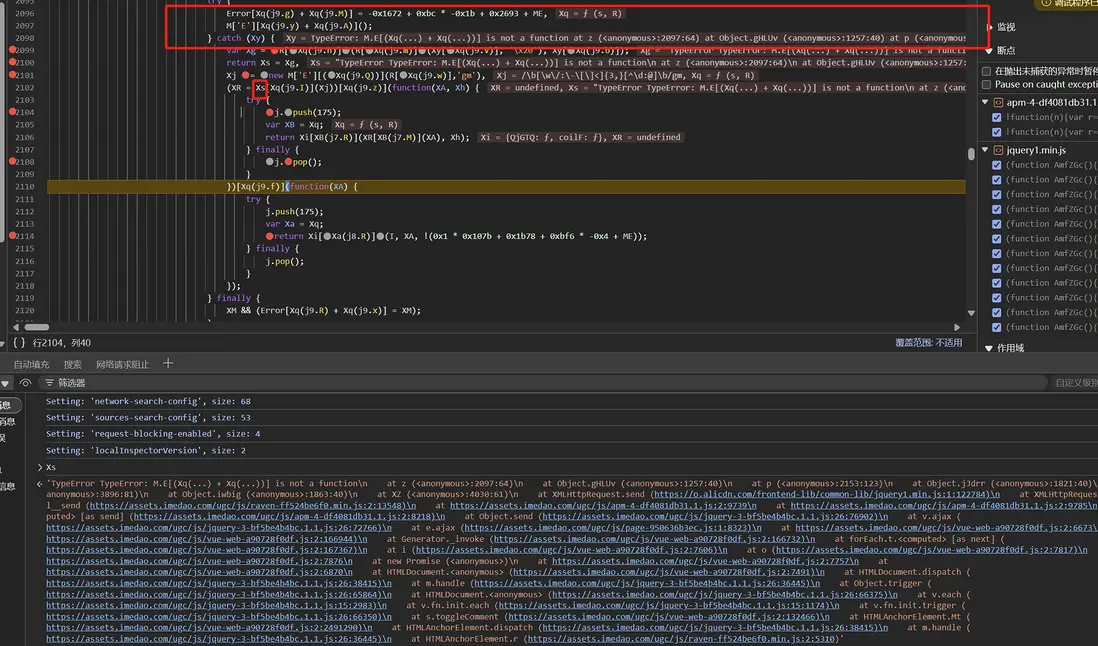
同時，發現在 F 值重置的時候，會調用 z 函數來生成 XR 值，在 z 函數內則是 Error 堆棧檢測，它會檢測你是哪個函數調用報錯的：

堆棧不同則最後生成的 XR 不同（隨機因子與 F 值初始化有關係，同時又與 XR 值有關係，XR 為錯誤堆棧檢測）。最終在這些值的加成下，讓 random 可以返回想要的值，如下圖：

隨後調用 X8 函數生成 Xb 值：

然後調用 XQ = R[ZJ(M4.H)](X8, Xm)) 方法，繼續由 x8 生成 XQ，這裏 random 還是一直輪着的，前面出現錯誤，那麼後面生成的參數都是錯的。

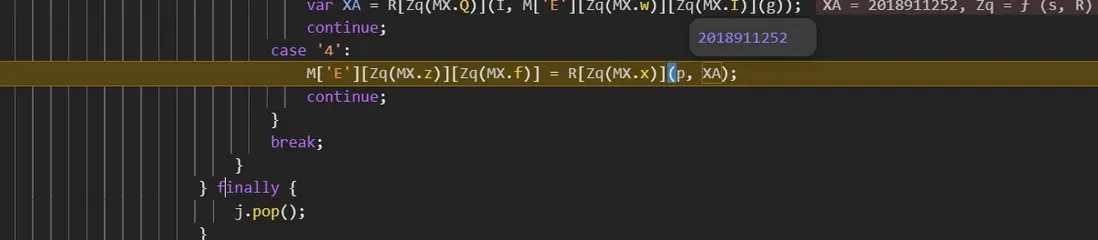
最終調用 XX, X0 完成 xb 值的拼接：

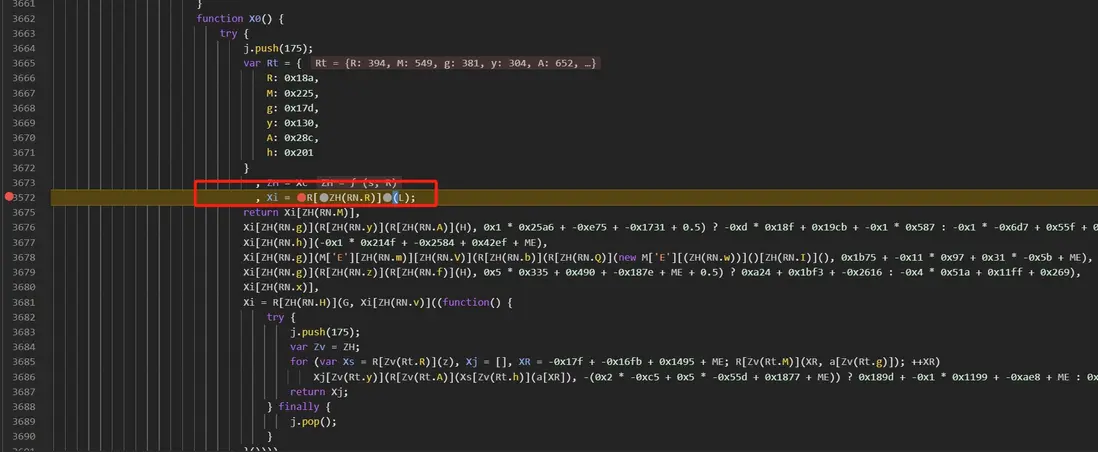
Xb = [R[ZJ(M4.v)](XX, Xb), R[ZJ(M4.F)](XX, XQ), R[ZJ(M4.p)](X0), R[ZJ(M4.e)](new M['E'][(ZJ(M4.k))]()[ZJ(M4.G)](), ''), XV[ZJ(M4.J) + ZJ(M4.d)], XV[ZJ(M4.n) + ZJ(M4.S)], R[ZJ(M4.c)](f)][ZJ(M4.W)]('|');

主要講的就 X0，裏面檢測居多，其中最經典的就是調試或篡改檢測，進入 X0 函數，首先到了檢測函數 L：

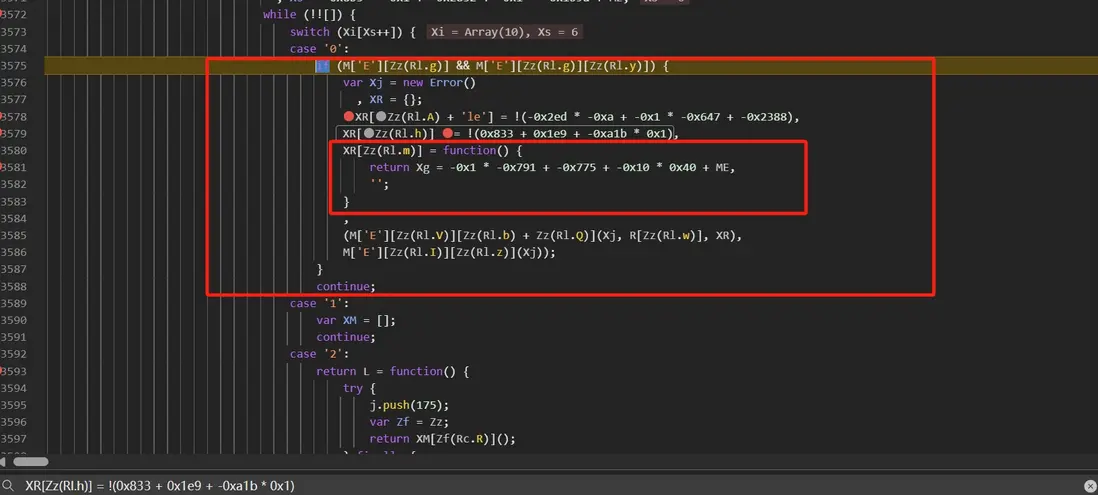
第一個便是反調試檢測，如下：

檢測代碼如下：

Xg = 0

var Xj = new Error()
    , XR = {};
XR["configurable"] = !(-0x2ed * -0xa + -0x1 * -0x647 + -0x2388);
XR["enumerable"] = !(0x833 + 0x1e9 + -0xa1b * 0x1);
XR["get"] = function () {
    console.log("觸發")
    return Xg = -0x1 * -0x791 + -0x775 + -0x10 * 0x40 + 997,
        '';
}
    ,
    (Object["defineProperty"](Xj, "stack", XR), console.debug(Xj))


console.log(Xg)

正常運行這段代碼會將 Xg 的值設置為 1，即被檢測，過掉這個檢測且不影響原代碼的情況下，只需加一行 console.debug=function (){} 即可過掉，如果不加，你最後扣下來的 1038 是用不了的。

隨後進入到了一系列 node 的環境檢測：

因為我們是扣代碼，所以只要照着瀏覽器去改就行了，全部弄好後，最終生成的 X0 值才是可用的。

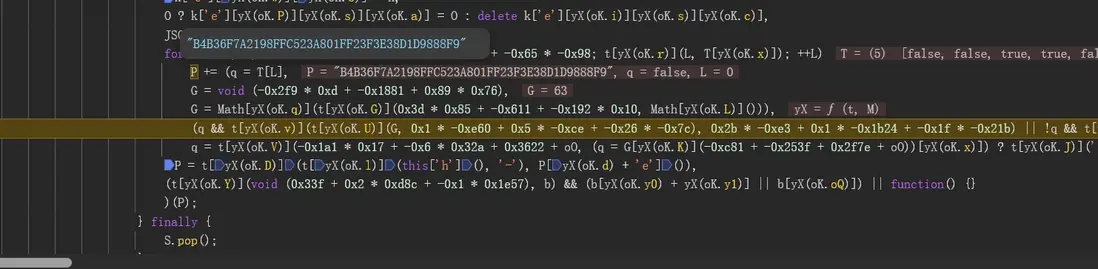
最後調用 J 函數，將拼接後的 Xb 傳入即可生成最終的值，但是這裏還有一個小坑，正常加密的時候，碼錶應該是 T 開頭的，但是如果沒有處理碼錶，加密出來的參數會對應不上：

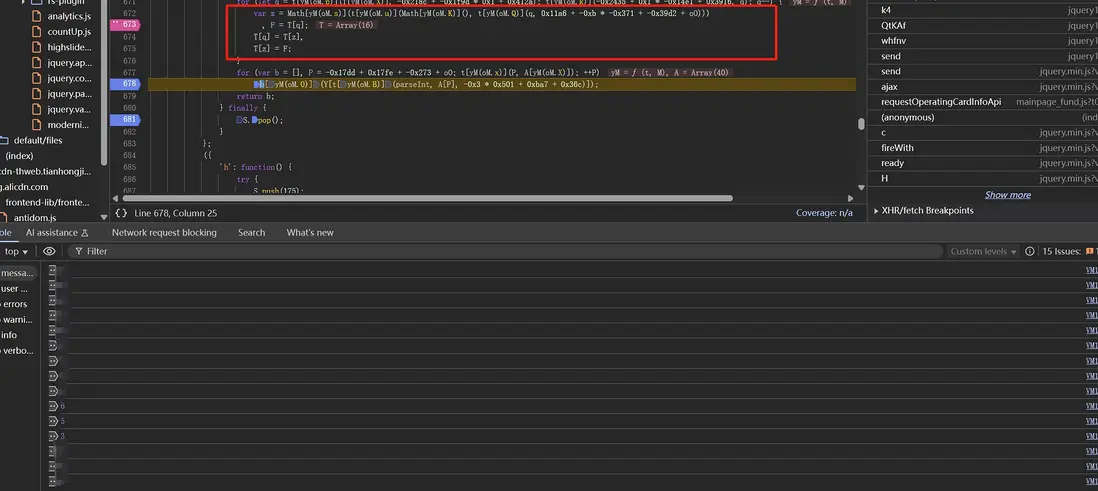
最終溯源發現碼錶經過了修改，先修改隨機因子：

然後 G 函數通過已隨機的因子將碼錶打亂，重新排序，得到正確的碼錶：

結果：

acw_sc__v2

acw_sc__v2 的難度在 1101 與 1038 之間，能搞定 1038 那麼新 v2 自然也是可以的，還是熟悉 debugger，這也是粉絲提問的：

還是老辦法，進行 js 替換：

替換後用 Hook 進行堆棧追蹤，發現最終的生成位置如下：

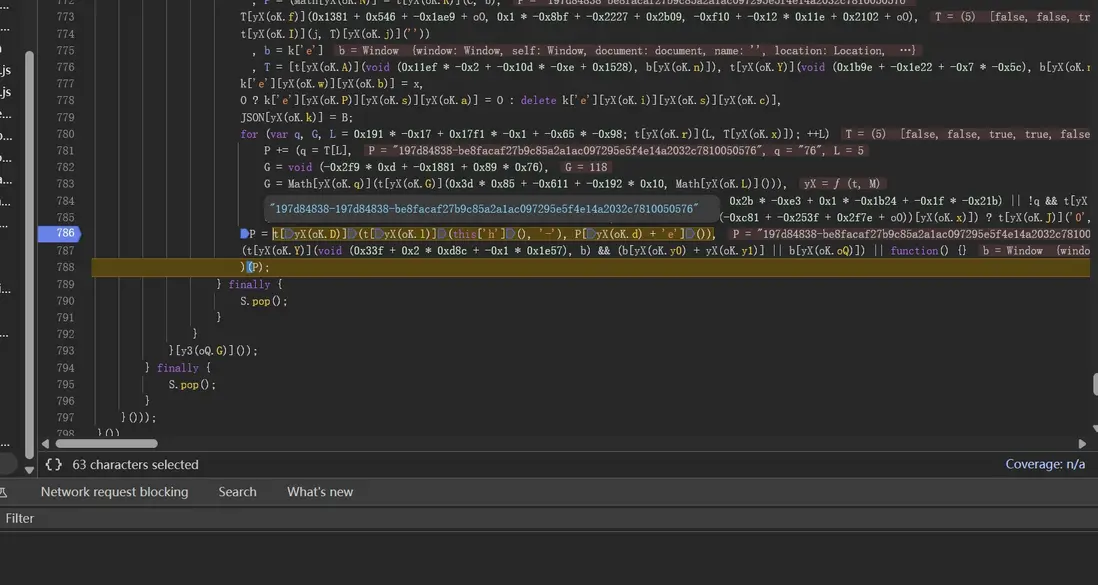
向上分析邏輯，發現還是先進行隨機設置（分析到後文不難看出這又是另一種混淆，讓它返回想返回的隨機數，與固定參數組合生成想要的值），T 的話，分析可知，仍然還是由 arg1 按照指定規則生成的，T = arg1[yX(oK.p)](-0x1640 + 0x701 * 0x2 + 0x1 * 0x5ec + oO, -0x9e4 + -0x53 * 0x35 + -0x38f * -0x7 + oO)[yX(oK.X)]('')：

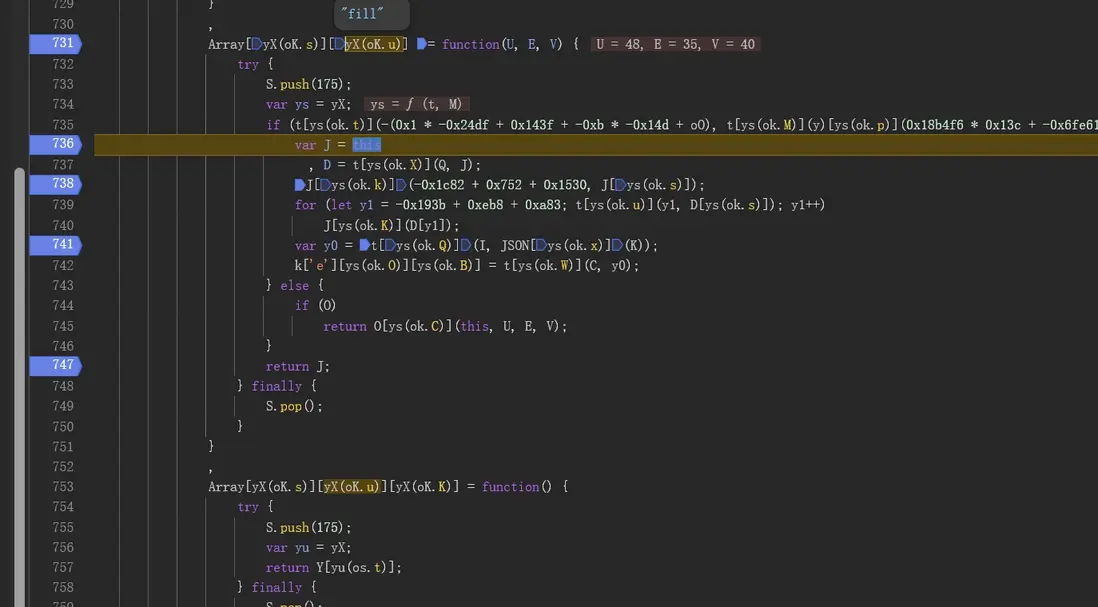
首先進入魔改後的 fiil 函數，將數組進行規則打亂後返回：

隨後利用設置好的隨機數再次將打亂後的數據按照指定規則排序（這裏可以記錄隨機數）：

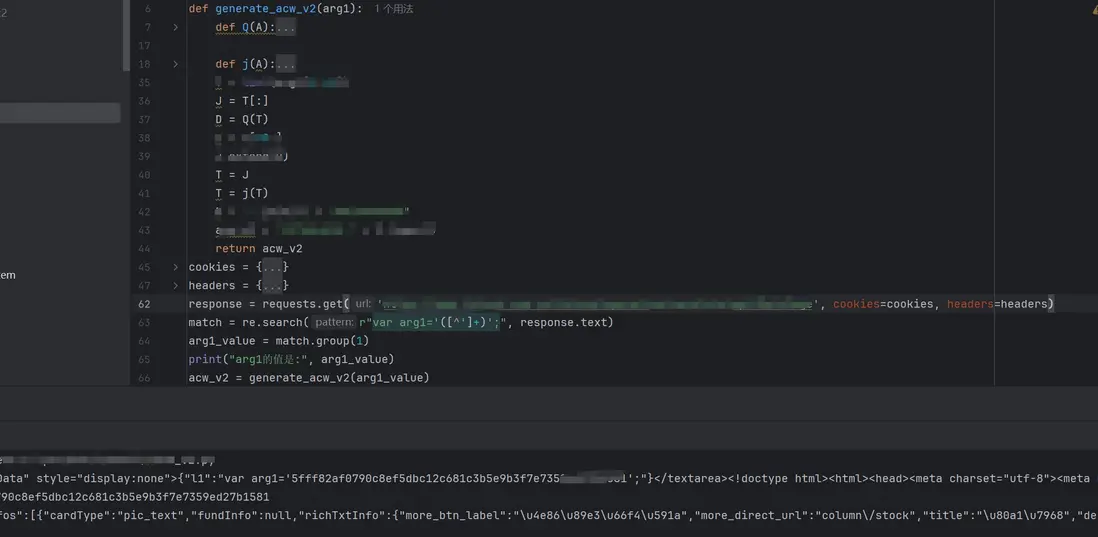
再拼接隨機文本數字，最終轉小寫後拼接生成，不管是 1101 還是 1038 亦或者 acw_sc__v2 參數，最終算法也都僅幾十行不過百行：

K哥爬蟲博客

K哥爬蟲博客

博客 / 詳情