- 機器學習基本理論
- 機器學習三要素
- 機器學習方法分類
- 建模流程
- 特徵工程
- 什麼是特徵工程
- 特徵工程有什麼
- 特徵選擇
- 特徵轉換
- 特徵構造
- 特徵降維
- 常用方法
- 模型評估和模型選擇
- 損失函數
- 經驗誤差
- 欠擬合和過擬合
- 正則化
- 交叉驗證
- 模型求解算法
- 解析法
- 梯度下降法
- 牛頓法和擬牛頓法
- 模型評價指標
- 迴歸模型評價指標
- 分類模型評價指標
機器學習基本理論
機器學習三要素
機器學習的方法一般主要由三部分構成:模型、策略和算法,可以認為:
機器學習方法 = 模型 + 策略 + 算法
- 模型(model):總結數據的內在規律,用數學語言描述的參數系統
- 策略(strategy):選取最優模型的評價準則
- 算法(algorithm):選取最優模型的具體方法
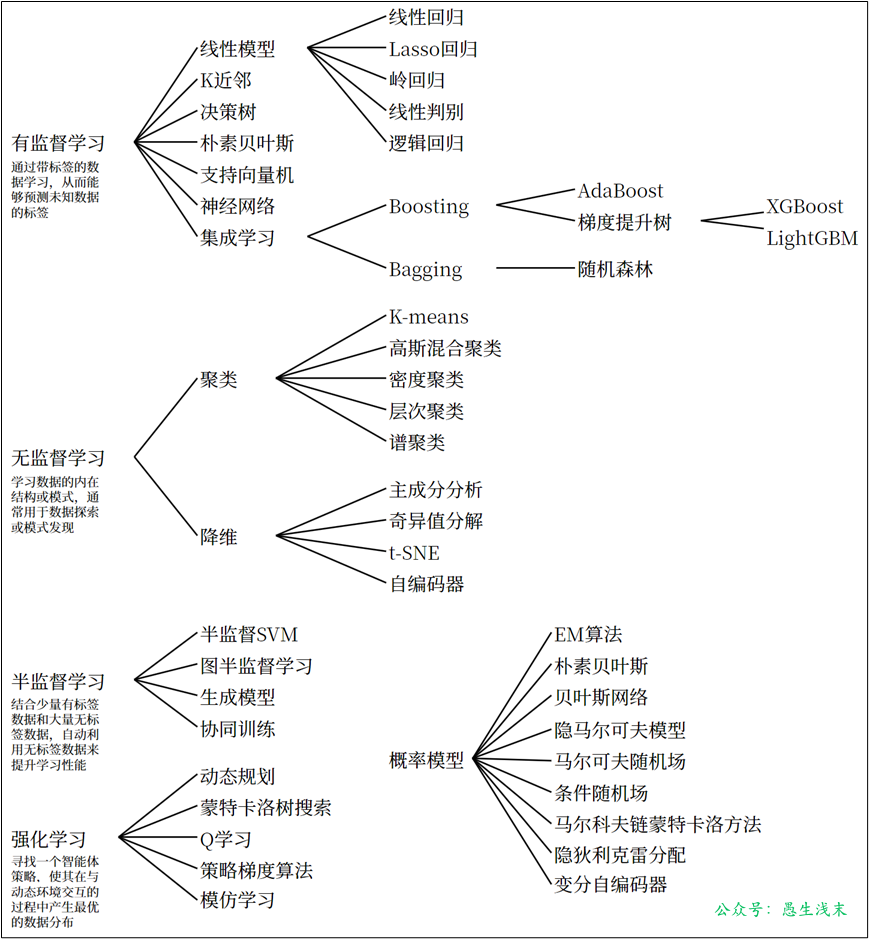
機器學習方法分類
機器學習的方法種類繁多,並不存在一個統一的理論體系能夠涵蓋所有內容。從不同的角度,可以將機器學習的方法進行不同的分類:
- 通常分類:按照有無監督,機器學習可以分為 有監督學習、無監督學習 和 半監督學習,除此之外還有 強化學習。
- 按模型分類:根據模型性質,可以分為概率模型/非概率模型,線性/非線性模型等。
- 按學習技巧分類:根據算法基於的技巧,可以分為貝葉斯學習、核方法等。
各種類型的機器學習方法可以用下圖彙總展示:
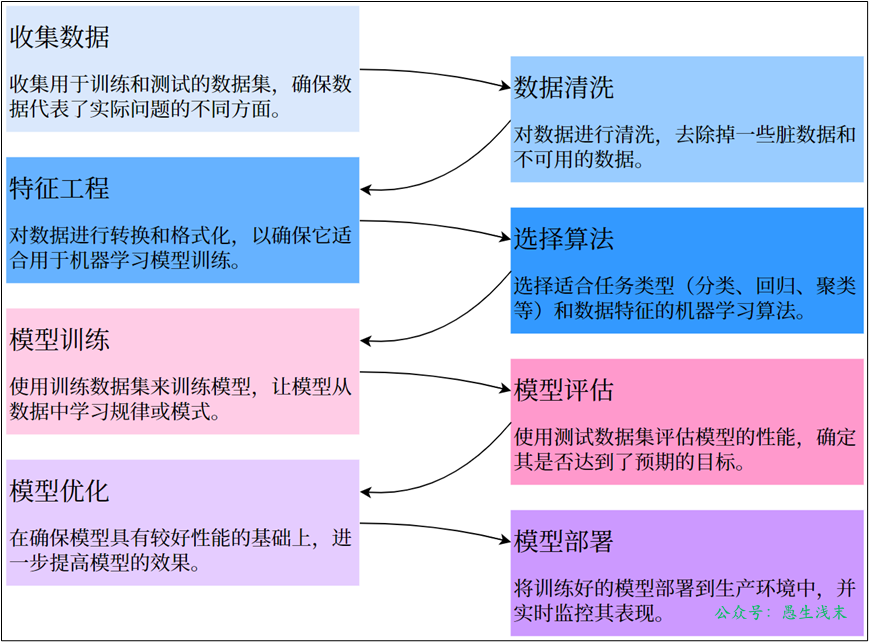
建模流程
以監督學習為例,考察一下機器學習的具體過程。
可以看到,機器學習是由數據驅動的,核心是利用數據來“訓練模型”;模型訓練的結果需要用一定的方法來進行評估、優化,最終得到一個成熟的學習模型;最後就可以用這個模型來進行預測和解決問題了。
監督學習建模的整體流程如下:
特徵工程
什麼是特徵工程
特徵工程(Feature Engineering)是機器學習過程中非常重要的一步,指的是通過對原始數據的處理、轉換和構造,生成新的特徵或選擇有效的特徵,從而提高模型的性能。簡單來説,特徵工程是將原始數據轉換為可以更好地表示問題的特徵形式,幫助模型更好地理解和學習數據中的規律。優秀的特徵工程可以顯著提高模型的表現;反之,忽視特徵工程可能導致模型性能欠佳。
實際上,特徵工程是一個迭代過程。特徵工程取決於具體情境。它需要大量的數據分析和領域知識。其中的原因在於,特徵的有效編碼可由所用的模型類型、預測變量與輸出之間的關係以及模型要解決的問題來確定。在此基礎上,輔以不同類型的數據集(如文本與圖像)則可能更適合不同的特徵工程技術。因此,要具體説明如何在給定的機器學習算法中最好地實施特徵工程可能並非易事。
特徵工程有什麼
特徵選擇
從原始特徵中挑選出與目標變量關係最密切的特徵,剔除冗餘、無關或噪聲特徵。這樣可以減少模型的複雜度、加速訓練過程、並減少過擬合的風險。
特徵選擇不會創建新特徵,也不會改變數據結構。
(1)過濾法(Filter Method)
基於統計測試(如卡方檢驗、相關係數、信息增益等)來評估特徵與目標變量之間的關係,選擇最相關的特徵。
(2)包裹法(Wrapper Method)
使用模型(如遞歸特徵消除 RFE)來評估特徵的重要性,並根據模型的表現進行特徵選擇。
(3)嵌入法(Embedded Method)
使用模型本身的特徵選擇機制(如決策樹的特徵重要性,L1正則化的特徵選擇)來選擇最重要的特徵。
特徵轉換
對數據進行數學或統計處理,使其變得更加適合模型的輸入要求。
(1)歸一化(Normalization)
將特徵縮放到特定的範圍(通常是0到1之間)。適用於對尺度敏感的模型(如KNN、SVM)。
(2)標準化(Standardization)
通過減去均值併除以標準差,使特徵的分佈具有均值0,標準差1。
(3)對數變換
對於有偏態的分佈(如收入、價格等),對數變換可以將其轉化為更接近正態分佈的形式。
(4)類別變量的編碼
獨熱編碼(One-Hot Encoding):將類別型變量轉換為二進制列,常用於無序類別特徵。
標籤編碼(Label Encoding):將類別型變量映射為整數,常用於有序類別特徵。
目標編碼(Target Encoding):將類別變量的每個類別替換為其對應目標變量的平均值或其他統計量。
頻率編碼(Frequency Encoding):將類別變量的每個類別替換為該類別在數據集中的出現頻率。
特徵構造
特徵構造是基於現有的特徵創造出新的、更有代表性的特徵。通過組合、轉換、或者聚合現有的特徵,形成能夠更好反映數據規律的特徵。
(1)交互特徵
將兩個特徵組合起來,形成新的特徵。例如,兩個特徵的乘積、和或差等。
例如,將年齡與收入結合創建新的特徵,可能能更好地反映某些模式。
(2)統計特徵
從原始特徵中提取統計值,例如求某個時間窗口的平均值、最大值、最小值、標準差等。
例如,在時間序列數據中,你可以從原始數據中提取每個小時、每日的平均值。
(3)日期和時間特徵
從日期時間數據中提取如星期幾、月份、年份、季度等特徵。
例如,將“2000-01-01”轉換為“星期幾”、“是否節假日”、“月初或月末”等特徵。
特徵降維
當數據集的特徵數量非常大時,特徵降維可以幫助減少計算複雜度並避免過擬合。通過降維方法,可以在保持數據本質的情況下減少特徵的數量。
(1)主成分分析(PCA)
通過線性變換將原始特徵映射到一個新的空間,使得新的特徵(主成分)儘可能地保留數據的方差。
(2)線性判別分析(LDA)
一種監督學習的降維方法,通過最大化類間距離與類內距離的比率來降維。
(3)t-SNE(t-Distributed Stochastic Neighbor Embedding,t分佈隨機近鄰嵌入)
一種非線性的降維技術,特別適合可視化高維數據。
(4)自編碼器(Auto Encoder)
一種神經網絡模型,通過壓縮編碼器來實現數據的降維。
常用方法
對於一個模型來説,有些特徵可能很關鍵,而有些特徵可能用處不大。
例如:
某個特徵取值較接近,變化很小,可能與結果無關。
某幾個特徵相關性較高,可能包含冗餘信息。
因此,特徵選擇 在特徵工程中是最基本、也最常見的操作。
另外,在訓練模型時有時也會遇到維度災難,即特徵數量過多。我們希望能在確保不丟失重要特徵的前提下減少維度的數量,來降低訓練模型的難度。所以在特徵工程中,也經常會用到 特徵降維 方法。
1)低方差過濾法
對於特徵的選擇,可以直接基於方差來判斷,這是最簡單的。低方差的特徵意味着該特徵的所有樣本值幾乎相同,對預測影響極小,可以將其去掉。
👉示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/feature/1-variance_filter.ipynb
from sklearn.feature_selection import VarianceThreshold
# 低方差過濾:刪除方差低於 0.01 的特徵
var_thresh = VarianceThreshold(threshold=0.01)
X_filtered = var_thresh.fit_transform(X)
2)相關係數法
通過計算特徵與目標變量或特徵之間的相關性,篩選出高相關性特徵(與目標相關)或剔除冗餘特徵(特徵間高度相關)。
- 皮爾遜相關係數
皮爾遜相關係數(Pearson Correlation)用於衡量兩個變量的線性相關性,取值範圍\([-1,1]\)
\(r = \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n}(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i - \bar{y})^2}}\)
- 正相關:值接近1,説明特徵隨目標變量增加而增加。
- 負相關:值接近-1,説明特徵隨目標變量增加而減少。
- 無關:值接近0,説明特徵和目標變量無明顯關係。
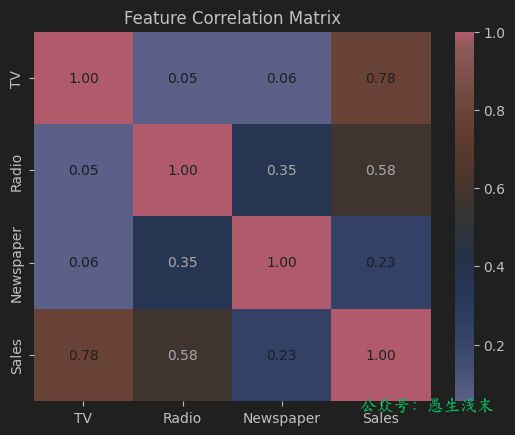
例如,現有一數據集包括不同渠道廣告投放金額與銷售額。
👉示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/feature/2_pearson.ipynb
使用pandas.DataFrame.corrwith(method="pearson")計算各個特徵與標籤間的皮爾遜相關係數。
import pandas as pd
advertising = pd.read_csv("data/advertising.csv")
advertising.drop(advertising.columns[0], axis=1, inplace=True)
advertising.dropna(inplace=True)
X = advertising.drop("Sales", axis=1)
y = advertising["Sales"]
# 計算皮爾遜相關係數
print(X.corrwith(y, method="pearson"))
# TV 0.782224
# Radio 0.576223
# Newspaper 0.228299
# dtype: float64
使用pandas.DataFrame.corr(method="pearson")計算皮爾遜相關係數矩陣。
import seaborn as sns
import matplotlib.pyplot as plt
# 計算皮爾遜相關係數矩陣
corr_matrix = advertising.corr(method="pearson")
# 可視化熱力圖
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title("Feature Correlation Matrix")
plt.show()
- 斯皮爾曼相關係數
斯皮爾曼相關係數(Spearman’s Rank Correlation Coefficient)的定義是等級變量之間的皮爾遜相關係數。用於衡量兩個變量之間的單調關係,即當一個變量增加時,另一個變量是否總是增加或減少(不要求是線性關係)。適用於非線性關係或數據不符合正態分佈的情況。
\(r_s = 1 - \frac{6 \sum d_i2}{n(n2 - 1)}\)
其中:
- $ d_i$ 是兩個變量的等級之差
- \(n\) 是樣本數
斯皮爾曼相關係數的取值範圍為 \([-1, 1]\):
- \(\rho = 1\):完全正相關(一個變量增加,另一個變量也總是增加)。
- \(\rho = -1\):完全負相關(一個變量增加,另一個變量總是減少)。
- \(\rho = 0\):無相關性。
例如,現有一組每週學習時長與數學考試成績的數據:
👉示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/feature/3_spearman.ipynb
| \(X\) | \(y\) |
|---|---|
| 5 | 55 |
| 8 | 65 |
| 10 | 70 |
| 12 | 75 |
| 15 | 85 |
| 3 | 50 |
| 7 | 60 |
| 9 | 72 |
| 14 | 80 |
| 6 | 58 |
按數值由小到大排出X、y的等級,並計算等級差:
| \(X\) | \(R_X\) | \(y\) | \(R_y\) | \(d = R_X - R_y\) | \(d^2\) |
|---|---|---|---|---|---|
| 5 | 2 | 55 | 2 | 0 | 0 |
| 8 | 5 | 65 | 5 | 0 | 0 |
| 10 | 7 | 70 | 6 | 1 | 1 |
| 12 | 8 | 75 | 8 | 0 | 0 |
| 15 | 10 | 85 | 10 | 0 | 0 |
| 3 | 1 | 50 | 1 | 0 | 0 |
| 7 | 4 | 60 | 4 | 0 | 0 |
| 9 | 6 | 72 | 7 | \(-1\) | 1 |
| 14 | 9 | 80 | 9 | 0 | 0 |
| 6 | 3 | 58 | 3 | 0 | 0 |
使用pandas.DataFrame.corrwith(method="spearman")計算斯皮爾曼相關係數。
import pandas as pd
# 每週學習時長
X = [[5], [8], [10], [12], [15], [3], [7], [9], [14], [6]]
# 數學考試成績
y = [55, 65, 70, 75, 85, 50, 60, 72, 80, 58]
# 計算斯皮爾曼相關係數
X = pd.DataFrame(X)
y = pd.Series(y)
print(X.corrwith(y, method="spearman"))
# 0.987879
- 主成分分析(PCA)
主成分分析(Principal Component Analysis,PCA)是一種常用的降維技術,通過線性變換將高維數據投影到低維空間,同時保留數據的主要變化模式。
使用sklearn.decomposition.PCA進行主成分分析。參數n_components若為小數則表示保留多少比例的信息,為整數則表示保留多少個維度。
👉示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/feature/4_pca.ipynb
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
n_samples = 1000
# 第1個主成分方向
component1 = np.random.normal(0, 1, n_samples)
# 第2個主成分方向
component2 = np.random.normal(0, 0.2, n_samples)
# 第3個方向(噪聲,方差較小)
noise = np.random.normal(0, 0.1, n_samples)
# 構造3維數據
X = np.vstack([component1 - component2, component1 + component2, component2 + noise]).T
# 標準化
scaler = StandardScaler()
X_standardized = scaler.fit_transform(X)
# 應用PCA,將3維數據降維到2維
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_standardized)
# 可視化
# 轉換前的3維數據可視化
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121, projection="3d")
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c="g")
ax1.set_title("Before PCA (3D)")
ax1.set_xlabel("Feature 1")
ax1.set_ylabel("Feature 2")
ax1.set_zlabel("Feature 3")
# 轉換後的2維數據可視化
ax2 = fig.add_subplot(122)
ax2.scatter(X_pca[:, 0], X_pca[:, 1], c="g")
ax2.set_title("After PCA (2D)")
ax2.set_xlabel("Principal Component 1")
ax2.set_ylabel("Principal Component 2")
plt.show()
模型評估和模型選擇
損失函數
對於模型一次預測結果的好壞,需要有一個度量標準。
對於監督學習而言,給定一個輸入X,選取的模型就相當於一個“決策函數”f,它可以輸出一個預測結果f(X),而真實的結果(標籤)記為Y。f(X) 和Y之間可能會有偏差,我們就用一個損失函數(loss function)來度量預測偏差的程度,記作 L(Y,f(X))。
損失函數用來衡量模型預測誤差的大小;損失函數值越小,模型就越好;
損失函數是f(X)和Y的非負實值函數;
常見損失函數
-
0-1 損失
\[L(Y, f(X)) = \begin{cases} 1, & Y \neq f(X) \\[4pt] 0, & Y = f(X) \end{cases} \] -
平方損失
\[L(Y, f(X)) = (Y - f(X))^2 \] -
絕對損失
\[L(Y, f(X)) = |Y - f(X)| \] -
對數似然損失
\[L(Y, P(Y|X)) = -\log P(Y|X) \]
經驗誤差
給定一個訓練數據集,數據個數為 \(n\):
根據選取的損失函數,就可以計算出模型 \(f(X)\) 在訓練集上的平均誤差,稱為訓練誤差,也被稱作 經驗誤差(empirical error) 或 經驗風險(empirical risk)。
類似地,在測試數據集上平均誤差,被稱為測試誤差或者 泛化誤差(generalization error)。
一般情況下對模型評估的策略,就是考察經驗誤差;當經驗風險最小時,就認為取到了最優的模型。這種策略被稱為 經驗風險最小化(empirical risk minimization,ERM)。
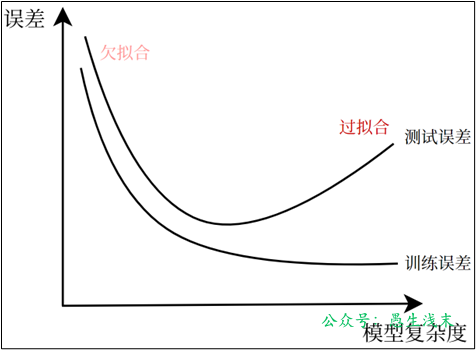
欠擬合和過擬合
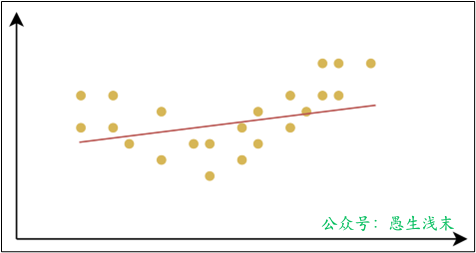
擬合(Fitting)是指機器學習模型在訓練數據上學習到規律並生成預測結果的過程。理想情況下,模型能夠準確地捕捉訓練數據的模式,並且在未見過的新數據(測試數據)上也有良好的表現;即模型具有良好的 泛化能力。
欠擬合(Underfitting):是指模型在訓練數據上表現不佳,無法很好地捕捉數據中的規律。這樣的模型不僅在訓練集上表現不好,在測試集上也同樣表現差。
過擬合(Overfitting):是指模型在訓練數據上表現得很好,但在測試數據或新數據上表現較差的情況。過擬合的模型對訓練數據中的噪聲或細節過度敏感,把訓練樣本自身的一些特點當作了所有潛在樣本都會具有的一般性質,從而失去了泛化能力。
產生欠擬合和過擬合的根本原因,是模型的複雜度過低或過高,從而導致測試誤差(泛化誤差)偏大。
- 欠擬合:模型在訓練集和測試集上誤差都比較大。模型過於簡單,高偏差。
- 過擬合:模型在訓練集上誤差較小,但在測試集上誤差較大。模型過於複雜,高方差。
1)產生原因與解決辦法
(1)欠擬合
產生原因:
- 模型複雜度不足:模型過於簡單,無法捕捉數據中的複雜關係。
- 特徵不足:輸入特徵不充分,或者特徵選擇不恰當,導致模型無法充分學習數據的模式。
- 訓練不充分:訓練過程中迭代次數太少,模型沒有足夠的時間學習數據的規律。
- 過強的正則化:正則化項設置過大,強制模型過於簡單,導致模型無法充分擬合數據。
解決辦法:
- 增加模型複雜度:選擇更復雜的模型。
- 增加特徵或改進特徵工程:添加更多的特徵或通過特徵工程來創造更有信息量的特徵。
- 增加訓練時間:增加訓練的迭代次數,讓模型有更多機會去學習。
- 減少正則化強度:如果使用了正則化,嘗試減小正則化的權重,以讓模型更靈活。
(2)過擬合
產生原因:
- 模型複雜度過高:模型過於複雜,參數太多。
- 訓練數據不足:數據集太小,模型能記住訓練數據的細節,但無法泛化到新數據。
- 特徵過多:特徵太多,模型可能會“記住”數據中的噪聲,而不是學到真正的規律。
- 訓練過長:訓練時間過長,導致模型學習到訓練數據中的噪聲,而非數據的真正規律。
解決辦法:
- 減少模型複雜度:降低模型的參數數量、使用簡化的模型或降維來減小模型複雜度。
- 增加訓練數據:收集更多數據,或通過數據增強來增加訓練數據的多樣性。
- 使用正則化:引入L1、L2正則化,避免過度擬合訓練數據。
- 交叉驗證:使用交叉驗證技術評估模型在不同數據集上的表現,以減少過擬合的風險。
- 早停:訓練時,當模型的驗證損失不再下降時,提前停止訓練,避免過度擬合訓練集。
2)示例代碼
使用多項式在 $ x \in [-3,3] $ 上擬合 \(sin(x)\)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression #現行迴歸模型
from sklearn.preprocessing import PolynomialFeatures #構建多項式特徵
from sklearn.model_selection import train_test_split #花粉訓練集和測試集
from sklearn.metrics import mean_squared_error #均方誤差損失函數
"""
1.生成數據
2.劃分訓練接和測試集
3.定義模型(線性迴歸模型)
4.訓練模型
5.預算結果,計算誤差
"""
plt.rcParams['font.sans-serif']=['KaiTi']
plt.rcParams['axes.unicode_minus']=False
#1.生成數據
X = np.linspace(-3,3,300).reshape(-1,1)
Y = np.sin(X) + np.random.uniform(low=-0.5,high=0.5,size=300).reshape(-1,1)
print(X.shape)
print(Y.shape)
#畫出散點圖(三個子圖)
fig,ax = plt.subplots(1,3,figsize = (15,4))
ax[0].scatter(X,Y,c='y')
ax[1].scatter(X,Y,c='y')
ax[2].scatter(X,Y,c='y')
#2.劃分訓練集和測試集
trainX,testX,trainY,testY=train_test_split(X,Y,test_size=0.2,random_state=42)
#3.定義模型(現行迴歸模型)
model1 = LinearRegression()
model2 = LinearRegression()
model3 = LinearRegression()
#一、欠擬合(直線)
x_train1 = trainX
x_test1 = testX
#恰好擬合(5次多項式)
poly5 = PolynomialFeatures(degree=5)
x_train2 = poly5.fit_transform(trainX)
x_test2 = poly5.fit_transform(testX)
#過擬合(20次多項式)
poly20 = PolynomialFeatures(degree=20)
x_train3 = poly20.fit_transform(trainX)
x_test3 = poly20.fit_transform(testX)
#4.訓練模型
model1.fit(x_train1,trainY)
model2.fit(x_train2,trainY)
model3.fit(x_train3,trainY)
#打印查看模型參數
print(model1.coef_)
print(model1.intercept_)
#5.預測結果,計算誤差
y_pred1 = model1.predict(x_test1)
test_loss1 = mean_squared_error(testY,y_pred1)
train_loss1 = mean_squared_error(trainY,model1.predict(x_train1))
y_pred2 = model2.predict(x_test2)
test_loss2 = mean_squared_error(testY,y_pred2)
train_loss2 = mean_squared_error(trainY,model2.predict(x_train2))
y_pred3 = model3.predict(x_test3)
test_loss3 = mean_squared_error(testY,y_pred3)
train_loss3 = mean_squared_error(trainY,model3.predict(x_train3))
#畫出擬合曲線並寫出訓練誤差和測試誤差
ax[0].plot(X,model1.predict(X),c='r')
ax[0].text(-3,1,f"測試誤差:{test_loss1:.4f}")
ax[0].text(-3,1.3,f"訓練誤差{train_loss1:.4f}")
ax[1].plot(X,model2.predict(poly5.fit_transform(X)),c='r')
ax[1].text(-3,1,f"測試誤差:{test_loss2:.4f}")
ax[1].text(-3,1.3,f"訓練誤差{train_loss2:.4f}")
ax[2].plot(X,model3.predict(poly20.fit_transform(X)),c='r')
ax[2].text(-3,1,f"測試誤差:{test_loss3:.4f}")
ax[2].text(-3,1.3,f"訓練誤差{train_loss3:.4f}")
plt.show()
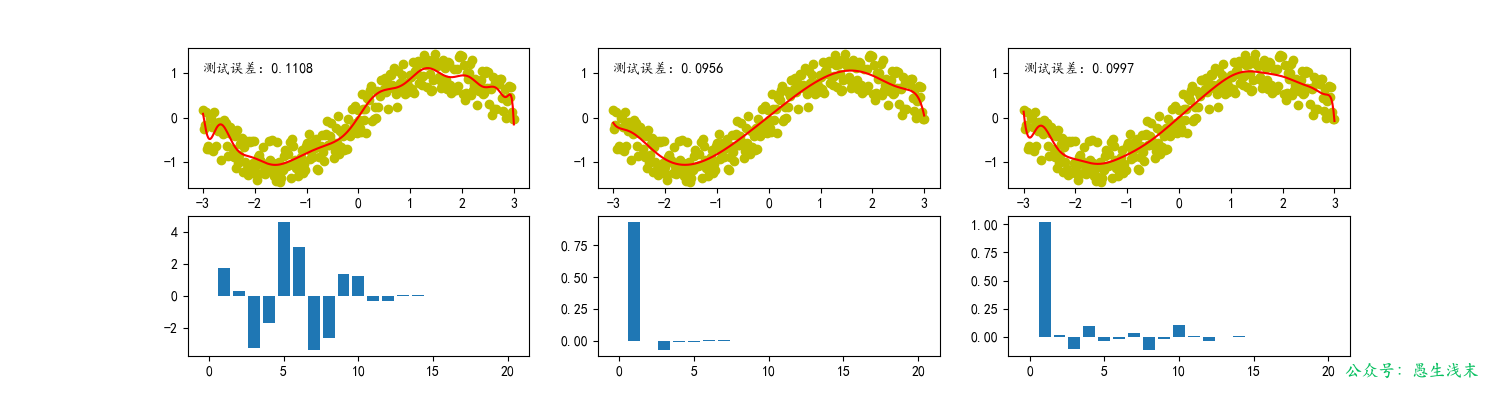
- 當多項式次數較低時,模型過於簡單,擬合效果較差。
- 當多項式次數增加後,模型複雜度適中,擬合效果較好,訓練誤差和測試誤差均較低。
- 當多項式次數繼續增加,模型變得過於複雜,過度學習了噪聲,導致訓練誤差較低而測試誤差較高。
正則化
正則化(Regularization)是一種在訓練機器學習模型時,在損失函數中添加額外項,來懲罰過大的參數,進而限制模型複雜度、避免過擬合,提高模型泛化能力的技術。
如在平方損失函數中加入正則化項\(\lambda \sum_{i=1}^{k}\omega_{i}^{2}\):
- 原損失函數\(\sum_{i = 1}^{n}(f(x_{i}) - y_{i})^{2}\)的目的:更好的擬合數據集。
- 正則化項\(\lambda \sum_{i = 1}^{k}\omega_{i}^{2}\)的目的:減小參數的大小,從而降低模型的複雜度。
這裏的\(\lambda\)是 正則化係數,用來表示懲罰項的權重。正則化係數不屬於模型的參數,無法通過訓練學習得到,需要在模型訓練開始之前手動設置,這種參數被稱為“超參數”。
兩者相互平衡,在模型的擬合能力(偏差)和複雜度之間找到最佳折中。
常見的正則化技術有L1正則化和L2正則化。
1)L1正則化(Lasso迴歸)
L1正則化在損失函數中加入參數的絕對值之和:
$ Loss_{L1} = 原Loss + \lambda\sum_{i = 1}^{k}|\omega_{i}| $
L1 正則化通過懲罰模型參數的絕對值,使得部分權重趨近 0 甚至變為 0。這會導致特徵選擇,即模型會自動“丟棄”一些不重要的特徵。L1 正則化有助於創建稀疏模型(即許多參數為 0)。在解決迴歸問題時,使用 L1 正則化也被稱為 “Lasso 迴歸”。
\(\lambda\) 超參數控制着正則化的強度。較大的 \(\lambda\) 值意味着強烈的正則化,會使模型更簡單,可能導致欠擬合。而較小的 \(\lambda\) 值則會使模型更復雜,可能導致過擬合。
2)L2 正則化(Ridge 迴歸,嶺迴歸)
L2 正則化在損失函數中加入參數的平方之和:
L2 正則化通過懲罰模型參數的平方,使得所有參數都變得更小,但不會將參數強行壓縮為 0。它會使得模型儘量平滑,從而防止過擬合。
在解決迴歸問題時,使用 L2 正則化也被稱為“嶺迴歸”。
3)ElasticNet 正則化(彈性網絡迴歸)
ElasticNet 正則化結合了 L1 和 L2 正則化,通過調整兩個正則化項的比例來取得平衡,從而同時具備稀疏性和穩定性的優點。
\(\alpha \in [0,1]\),決定 L1 和 L2 的權重。
4)正則化案例
同樣以使用多項式在$ x \in [-3,3] \(上擬合\)\sin(x)$為例,分別不使用正則化、使用 L1 正則化、使用 L2 正則化進行擬合。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression,Lasso,Ridge #現行迴歸模型
from sklearn.preprocessing import PolynomialFeatures #構建多項式特徵
from sklearn.model_selection import train_test_split #花粉訓練集和測試集
from sklearn.metrics import mean_squared_error #均方誤差損失函數
"""
1.生成數據
2.劃分訓練接和測試集
3.定義模型(線性迴歸模型)
4.訓練模型
5.預算結果,計算誤差
"""
plt.rcParams['font.sans-serif']=['KaiTi']
plt.rcParams['axes.unicode_minus']=False
#1.生成數據
X = np.linspace(-3,3,300).reshape(-1,1)
Y = np.sin(X) + np.random.uniform(low=-0.5,high=0.5,size=300).reshape(-1,1)
#畫出散點圖(2x3 子圖)
fig,ax = plt.subplots(2,3,figsize = (15,4))
ax[0,0].scatter(X,Y,c='y')
ax[0,1].scatter(X,Y,c='y')
ax[0,2].scatter(X,Y,c='y')
#2.劃分訓練集和測試集
trainX,testX,trainY,testY=train_test_split(X,Y,test_size=0.2,random_state=42)
#過擬合(20次多項式)
poly20 = PolynomialFeatures(degree=20)
x_train = poly20.fit_transform(trainX)
x_test = poly20.fit_transform(testX)
#一、不加正則項
# 定義模型
model = LinearRegression()
#4.訓練模型
model.fit(x_train,trainY)
#5.預測結果,計算誤差
y_pred1 = model.predict(x_test)
test_loss1 = mean_squared_error(testY,y_pred1)
train_loss1 = mean_squared_error(trainY,model.predict(x_train))
#畫出擬合曲線並寫出訓練誤差和測試誤差
ax[0,0].plot(X,model.predict(poly20.fit_transform(X)),c='r')
ax[0,0].text(-3,1,f"測試誤差:{test_loss1:.4f}")
#畫出所有係數的直方圖
ax[1,0].bar(np.arange(21),model.coef_.reshape(-1))
#二、加L1正則化項(Lasso迴歸)
# 定義模型
lasso = Lasso(alpha=0.01)
#4.訓練模型
lasso.fit(x_train,trainY)
#5.預測結果,計算誤差
y_pred2 = lasso.predict(x_test)
test_loss2 = mean_squared_error(testY,y_pred2)
train_loss2 = mean_squared_error(trainY,lasso.predict(x_train))
#畫出擬合曲線並寫出訓練誤差和測試誤差
ax[0,1].plot(X,lasso.predict(poly20.fit_transform(X)),c='r')
ax[0,1].text(-3,1,f"測試誤差:{test_loss2:.4f}")
#畫出所有係數的直方圖
ax[1,1].bar(np.arange(21),lasso.coef_.reshape(-1))
#三、加L2正則化項(Ridge(嶺)迴歸)
# 定義模型
ridge = Ridge(alpha=1)
#4.訓練模型
ridge.fit(x_train,trainY)
#5.預測結果,計算誤差
y_pred3 = ridge.predict(x_test)
test_loss3 = mean_squared_error(testY,y_pred3)
train_loss3 = mean_squared_error(trainY,ridge.predict(x_train))
#畫出擬合曲線並寫出訓練誤差和測試誤差
ax[0,2].plot(X,ridge.predict(poly20.fit_transform(X)),c='r')
ax[0,2].text(-3,1,f"測試誤差:{test_loss3:.4f}")
#畫出所有係數的直方圖
ax[1,2].bar(np.arange(21),ridge.coef_.reshape(-1))
plt.show()
交叉驗證
交叉驗證(Cross-Validation)是一種評估模型泛化能力的方法,通過將數據集劃分為多個子集,反覆進行訓練和驗證,以減少因單次數據劃分帶來的隨機性誤差。通過交叉驗證能更可靠地估計模型在未知數據上的表現,亦能避免因單次數據劃分不合理導致的模型過擬合或欠擬合。
1)簡單交叉驗證(Hold-Out Validation)
將數據劃分為訓練集和驗證集(如70%訓練,30%驗證)。結果受單次劃分影響較大,可能高估或低估模型性能。
2)k折交叉驗證(k-Fold Cross-Validation)
將數據均勻分為k個子集(稱為“折”),每次用k−1折訓練,剩餘1折驗證,重複k次後取平均性能。充分利用數據,結果更穩定。
3)留一交叉驗證(Leave-One-Out,LOO)
每次僅留一個樣本作為驗證集,其餘全部用於訓練,重複直到所有樣本都被驗證一次。適用於小數據集,計算成本極高。
模型求解算法
正則化可以有效防止過擬合,增強模型的泛化能力。這時模型的評估策略,就是讓結構化的經驗風險最小,即增加了正則化項的損失函數最小,稱為結構風險最小化(Structural Risk Minimization,SRM)。
$\min \frac{1}{n}\left( \sum_{i=1}^{n} L(y_i, f(x_i)) + \lambda J(\theta) \right) $
這其實就是求解一個最優化問題。代入訓練集所有數據 $ (x_i, y_i) $ ,要求最小值的目標函數就是模型中參數$ \theta $ 的函數。 具體求解的算法,可以利用數學公式直接計算解析解,也可以使用迭代算法。
解析法
如果模型損失函數的最小值可以通過數學公式進行嚴格推導,得到一個解析解,那麼就直接得到了最優模型的全部參數。這種方法稱作解析法。
1)特點
- 適用條件:目標函數必須可導,且導數方程有解析解。
- 優點:直接且精確;計算高效;
- 缺點:適用條件較為苛刻;特徵維度較大時,矩陣求逆計算複雜度極高。
2)應用示例
- 線性迴歸問題:可以採用“最小二乘法”求得解析解。
\(Loss_{MSE} = \frac{1}{n}(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y})^T(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y}) \\\)
$ \nabla Loss_{MSE} = \frac{2}{n}\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y}) = 0 $
- 線性迴歸L2正則化(Ridge迴歸,嶺迴歸)
可以得到解析解如下:
$ Loss_{L2} = \frac{1}{n}(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y})^T(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y}) + \frac{1}{n}\lambda\boldsymbol{\beta}^T\boldsymbol{\beta} $
$ \nabla Loss_{L2} = \frac{2}{n}\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{\beta} - \boldsymbol{y}) + \frac{2}{n}\lambda\boldsymbol{\beta} = 0 $
由於加入的對角矩陣\(\lambda\boldsymbol{I}\)就像一條“山嶺”,因此L2正則化也稱作“嶺迴歸”。
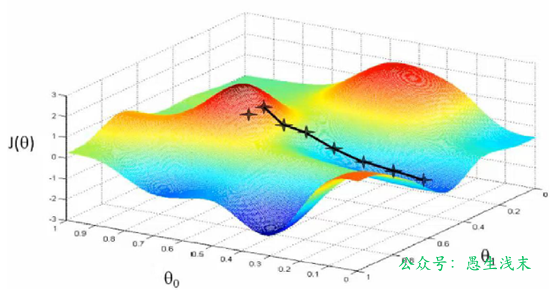
梯度下降法
梯度下降法(gradient descent)是一種常用的一階優化方法,是求解無約束優化問題最簡單、最經典的方法之一。梯度下降法是迭代算法,基本思路就是先選取一個適當的初始值θ_0,然後沿着梯度方向或者負梯度方向,不停地更新參數,最終取到極小值。
- 梯度方向:函數變化增長最快的方向(變量沿此方向變化時函數增長最快)
- 負梯度方向:函數變化減少最快的方向(變量沿此方向變化時函數減少最快)
因為損失函數是係數的函數,那麼如果係數沿着損失函數的負梯度方向變化,此時損失函數減少最快,能夠以最快速度下降到極小值。
$\theta_{k+1} = \theta_k - \alpha \cdot \nabla L(\theta_k) $
這裏的\(\nabla L(\theta_k)\)是參數取值為\(\theta_k\)時損失函數( L )的梯度;\(\alpha\)是每次迭代的“步長”,被稱為“學習率”。學習率也是一個常見的超參數,需要手動設置,選擇不當會導致收斂失敗。
1)特點 - 梯度下降不一定能夠找到全局的最優解,有可能是一個局部最優解。
- 優點:適用性廣;計算簡單;
- 缺點:收斂速度慢;可能陷入局部最優。
2)分類
①批量梯度下降(Batch Gradient Descent,BGD) 每次迭代使用全部訓練數據計算梯度。
-
優點:穩定收斂。
-
缺點:計算開銷大。
②隨機梯度下降(Stochastic Gradient Descent,SGD) 每次迭代隨機選取一個樣本計算梯度。
- 優點:速度快,適合大規模數據。
- 缺點:梯度更新方向不穩定,優化過程震盪較大,可能難以收斂。
③小批量梯度下降(Mini-batch Gradient Descent,MBGD) 每次迭代使用一小批樣本(如 32、64 個)計算梯度。 平衡了 BGD 的穩定性和 SGD 的速度,是最常用的方法。
3)梯度下降法計算步驟
(1)初始化參數:隨機選擇初始參數
(2)計算梯度:在當前參數下,計算損失函數的梯度
(3)更新參數:沿負梯度方向調整參數
(4)重複迭代:直到滿足停止條件(如梯度接近零、達到最大迭代次數等)
4)代碼實現
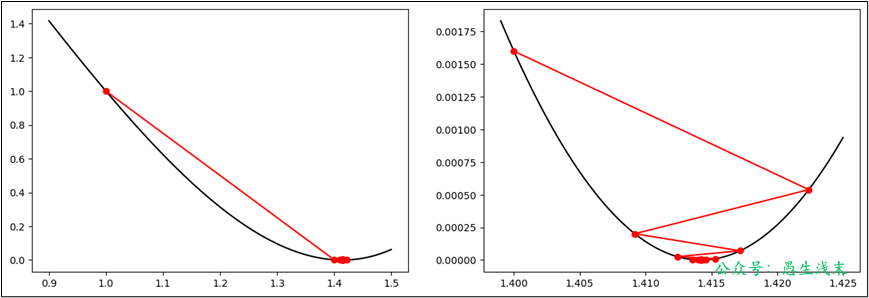
以一個單變量函數為例,介紹梯度下降法的代碼實現。
設 $ f(x) = x^2 $ ,求$ x$為何值時, $ f(x) = 2 $ 。 目標函數 $ J(x) = (f(x) - 2)^2 = (x^2 - 2)^2 $ ,原問題等價於求 $x $ 為何值時目標函數取得最小值。
使用梯度下降法求解。
-
\(x\)初始值取$ 1 $
-
學習率\(\alpha\)取$ 0.1 $
-
\(\frac{dJ(x)}{dx} = 2 \times (x^2 - 2) \times 2 \times x = 4x^3 - 8x\)
第 1 步: $ x_1 = 1 $ , $ J(x_1) = 1 $ , $ J(x_1)' = -4 $ , $ x_2 = x_1 - \alpha J(x_1)' = 1.4 $
第 2 步: $ x_2 = 1.4 $ , $ J(x_2) = 0.0016 $ , $ J(x_2)' = -0.2240 $ , $ x_3 = x_2 - \alpha J(x_2)' = 1.4224 $
\(\vdots\)第 $n $ 步: $ x_n = 1.414213 $ ,$ J(x_n) = 2.53 \times 10^{-12} $ ,$ J(x_n)' = 8.8817 \times 10^{-15} $
示例代碼:
-
https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/3_gradient_descent1.ipynb
-
https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/4_gradient_descent2.ipynb
-
5)應用示例
- L1正則化(Lasso迴歸)
梯度下降法求解的推導過程如下:
$ \frac{\partial Loss_{L1}}{\partial \omega_j} = \frac{1}{n}\left( 2\sum_{i=1}^{n}x_{ij}(f(\boldsymbol{x}_i) - y_i) + \lambda \cdot \text{sign}(\omega_j) \right) $
其中\(\text{sign}(\omega_j) = \begin{cases} 1, & \omega_j > 0 \\ 0, & \omega_j = 0 \\ -1, & \omega_j < 0 \end{cases}\)
參數更新:\(\omega_j \leftarrow \omega_j - \alpha\left( \frac{2}{n}\sum_{i=1}^{n}x_{ij}(f(\boldsymbol{x}_i) - y_i) + \frac{\lambda}{n} \cdot \text{sign}(\omega_j) \right)\)
可見L1正則化項的梯度是一個常數\(\frac{\lambda}{n}\),當\(\omega_j\)很小時會直接變成0,導致稀疏性。
- L2正則化(Ridge迴歸,嶺迴歸)
梯度下降法求解的推導過程如下:
$ \frac{\partial Loss_{L2}}{\partial \omega_j} = \frac{1}{n}\left( 2\sum_{i=1}^{n}x_{ij}(f(\boldsymbol{x}_i) - y_i) + 2\lambda\omega_j \right) $
梯度更新:\(\omega_j \leftarrow \omega_j - \alpha\left( \frac{2}{n}\sum_{i=1}^{n}x_{ij}(f(\boldsymbol{x}_i) - y_i) + \frac{2\lambda}{n}\omega_j \right)\)
可見 L2 正則化項的梯度是 \(\frac{2\lambda}{n}\omega_j\) ,相當於在每次更新時都對 \(\omega_j\) 進行縮小,但不會直接變為 0。
牛頓法和擬牛頓法
牛頓法也是求解無約束最優化問題的常用方法,核心思想是利用目標函數的二階導數信息,通過迭代逐漸逼近極值點。
$ \theta_{k+1} = \theta_k - H^{-1}(\theta_k) \cdot \nabla L(\theta_k) $
這裏的$ H^{-1}(\theta_k) $ 表示損失函數$ L $ 黑塞矩陣的逆在點$ \theta_k $的取值。
- 優點:收斂速度快;精度高;
- 缺點:計算複雜;可能發散。
由於牛頓法中需要計算黑塞矩陣的逆 $ H^{-1}(\theta_k) $ ,這一步比較複雜;所以可以考慮用一個$ n $ 階正定矩陣來近似代替它,這種方法稱為“擬牛頓法”。
牛頓法和擬牛頓法一般用於解決中小規模的凸優化問題。
模型評價指標
對學習的泛化性能進行評估,不僅需要有效可行的實驗估計方法,還需要有衡量模型泛化能力的評價指標,也叫做性能度量(performance measure)。
迴歸模型評價指標
模型的評價指標用於衡量模型在訓練集或測試集上的性能,評估結果反映了模型預測的準確性和泛化能力。
對於迴歸問題,最常用的性能度量是“均方誤差” (Mean Squared Error,MSE)。
1)平均絕對誤差(MAE)
$ MAE = \frac{1}{n}\sum_{i=1}^{n}|f(\boldsymbol{x}_i) - y_i| $
- MAE 對異常值不敏感,解釋直觀。適用於數據包含異常值的場景。
2)均方誤差(MSE)
$ MSE = \frac{1}{n}\sum_{i=1}^{n}(f(\boldsymbol{x}_i) - y_i)^2 $
- MSE 會放大較大誤差,對異常值敏感。適用於需要懲罰大誤差的場景。
3)均方根誤差(RMSE)
- 與 MSE 類似,但量綱與目標變量一致。適用於需要直觀誤差量綱的場景。如果一味地試圖降低 RMSE,可能會導致模型對異常值也擬合度很高,容易過擬合。
4)$ R^2 $(決定係數)
- 衡量模型對目標變量的解釋能力,越接近 1 越好,對異常值敏感。
分類模型評價指標
對於分類問題,最常用的指標就是“準確率”(Accuracy),它定義為分類器對測試集正確分類的樣本數與總樣本數之比。此外還有一系列常用的評價指標。
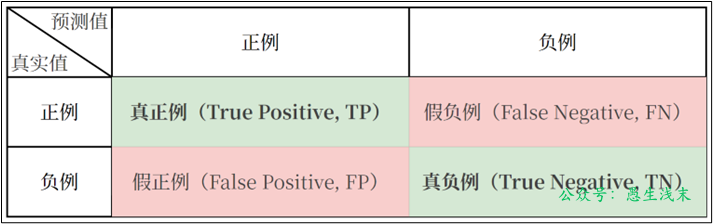
1)混淆矩陣
混淆矩陣(Confusion Matrix)是用於評估分類模型性能的工具,展示了模型預測結果與實際標籤的對比情況。
對於二分類問題,混淆矩陣是一個2×2矩陣:
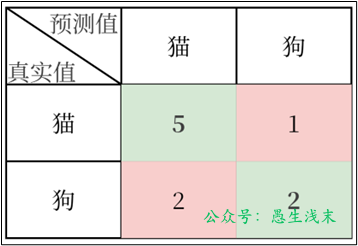
例如,有10個樣本。6個是貓,4個是狗。假設以貓為正例,模型預測對了5個貓,2個狗。
使用sklearn.metrics.confusion_matrix查看混淆矩陣:
示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/metrics/1_classification_test.ipynb
2)準確率(Accuracy)
正確預測的比例。
$Accuracy = \frac{TP + TN}{TP + TN + FP + FN} $
https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/metrics/1_classification_test.ipynb
該案例中準確率$ = \frac{5 + 2}{10} = 0.7 $
from sklearn.metrics import accuracy_score label = ["貓", "狗"] # 標籤 y_true = ["貓", "貓", "貓", "貓", "貓", "貓", "狗", "狗", "狗", "狗"] # 真實值 y_pred1 = ["貓", "貓", "狗", "貓", "貓", "貓", "貓", "貓", "狗", "狗"] # 預測值 accuracy = accuracy_score(y_true, y_pred1) print(accuracy)
3)精確率
預測為正例的樣本中實際為正例的比例,也叫查準率。
$ Precision = \frac{TP}{TP + FP} $
上述案例中,精確率$ = \frac{5}{5 + 2} = 0.7143 $
from sklearn.metrics import precision_score
label = ["貓", "狗"] # 標籤
y_true = ["貓", "貓", "貓", "貓", "貓", "貓", "狗", "狗", "狗", "狗"] # 真實值
y_pred1 = ["貓", "貓", "狗", "貓", "貓", "貓", "貓", "貓", "狗", "狗"] # 預測值
precision = precision_score(y_true, y_pred1, pos_label="貓") # pos_label指定正例
print(precision)
4)召回率(Recall)
實際為正類的樣本中預測為正類的比例,也叫查全率。
$ Recall = \frac{TP}{TP + FN} $
上述案例中,召回率$ = \frac{5}{5 + 1} = 0.8333 $
from sklearn.metrics import recall_score
label = ["貓", "狗"] # 標籤
y_true = ["貓", "貓", "貓", "貓", "貓", "貓", "狗", "狗", "狗", "狗"] # 真實值
y_pred1 = ["貓", "貓", "狗", "貓", "貓", "貓", "貓", "貓", "狗", "狗"] # 預測值
recall = recall_score(y_true, y_pred1, pos_label="貓") # pos_label指定正例
print(recall)
5)F1分數(F1Score)
精確率和召回率的調和平均。
$ F1\ Score = \frac{2 \times Precision \times Recall}{Precision + Recall} $
上述案例中,F1 分數$ = \frac{2 \times \frac{5}{5 + 2} \times \frac{5}{5 + 1}}{\frac{5}{5 + 2} + \frac{5}{5 + 1}} = 0.7692 $
from sklearn.metrics import f1_score
label = ["貓", "狗"] # 標籤
y_true = ["貓", "貓", "貓", "貓", "貓", "貓", "狗", "狗", "狗", "狗"] # 真實值
y_pred1 = ["貓", "貓", "狗", "貓", "貓", "貓", "貓", "貓", "狗", "狗"] # 預測值
f1 = f1_score(y_true, y_pred1, pos_label="貓") # pos_label指定正例
print(f1)
在代碼中,可通過sklearn.metrics.classification_report生成分類任務的評估報告,包括精確率、召回率、F1分數等。
from sklearn.metrics import classification_report
report = classification_report(y_true, y_pred, labels=[], target_names=None)
# y_true:真實標籤
# y_pred:預測的標籤
# labels:可選,指定需要計算的類別列表(默認計算所有出現過的類別)
# target_names:可選,類別名稱(默認使用 labels 指定的類別號)
示例代碼:https://gitee.com/kohler19/machine_-learn/blob/master/ch02_base/metrics/2_classification_report.py
6)ROC曲線
-
真正例率(TPR):實際為正例,被預測為正例的比例,即召回率。
-
假正例率(FPR):實際為負例,被預測為正例的比例。
-
閾值(Threshold):根據閾值將概率轉換為類別標籤。
$ TPR = \frac{TP}{\text{實際正例數}} = \frac{TP}{TP + FN} $
$ FPR = \frac{FP}{\text{實際負例數}} = \frac{FP}{FP + TN} $
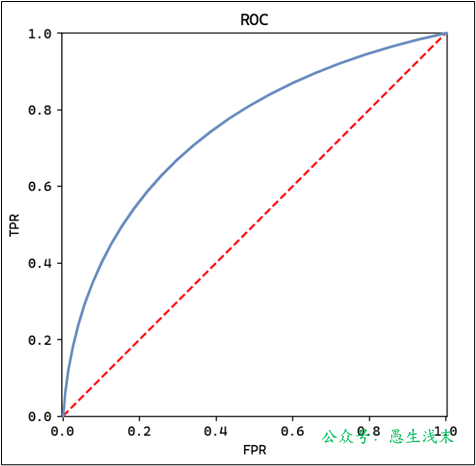
ROC曲線(Receiver Operating Characteristic Curve,受試者工作特徵)是評估二分類模型性能的工具,以假正例率(FPR)為橫軸,以真正例率(TPR)為縱軸,展示不同閾值下模型的表現。繪製ROC曲線時,從高到低調整閾值,計算每個閾值的TPR和FPR並繪製所有閾值的點,形成ROC曲線。
7)案例:繪製ROC曲線
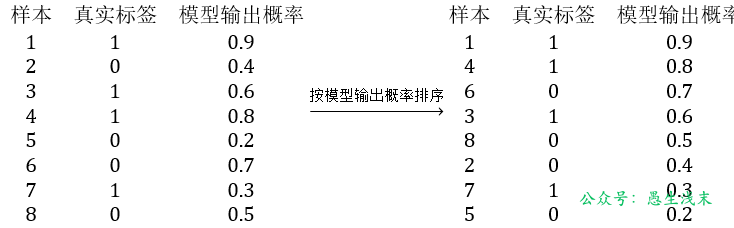
假設一個二分類模型的真實標籤和模型輸出概率如下:
調整閾值,計算 TPR 和 FPR:
閾值 = 0.9: $ TPR = \frac{0}{4} = 0 $ , $ FPR = \frac{0}{4} = 0 $ ,點座標 \((0,0)\)
閾值 = 0.8: $ TPR = \frac{1}{4} = 0.25 $ , $ FPR = \frac{0}{4} = 0 $ ,點座標 \((0, 0.25)\)
閾值 = 0.7: $ TPR = \frac{2}{4} = 0.5 $ , $ FPR = \frac{0}{4} = 0 $ ,點座標 \((0, 0.5)\)
閾值 = 0.6: $ TPR = \frac{2}{4} = 0.5 $ , $ FPR = \frac{1}{4} = 0.25 $ ,點座標 \((0.25, 0.5)\)
閾值 = 0.5: $ TPR = \frac{3}{4} = 0.75 $ , $ FPR = \frac{1}{4} = 0.25 $ ,點座標 \((0.25, 0.75)\)
閾值 = 0.4: $ TPR = \frac{3}{4} = 0.75 $ , $ FPR = \frac{2}{4} = 0.5 $ ,點座標 \((0.5, 0.75)\)
閾值 = 0.3: $ TPR = \frac{3}{4} = 0.75 $ , $ FPR = \frac{3}{4} = 0.75 $ ,點座標 \((0.75, 0.75)\)
閾值 = 0.2 :$ TPR = \frac{4}{4} = 1 $ , $ FPR = \frac{3}{4} = 0.75 $ ,點座標 $(0.75, 1) $
根據座標點繪製ROC曲線:
8)AUC值
AUC值代表ROC曲線下的面積,用於量化模型性能。AUC值越大,模型區分正負類的能力越強,模型性能越好。AUC值=0.5表示模型接近隨機猜測,AUC值=1代表完美模型。
可通過sklearn.metrics.roc_auc_score計算AUC值。
from sklearn.metrics import roc_auc_score
auc_score = roc_auc_score(y_true, y_score)
# y_true: 真實標籤(0 或 1)
# y_score: 正例的概率值或置信度
例如:
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
# 生成一個二分類數據集
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=100)
# 劃分訓練集和測試集
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=100)
# 訓練一個邏輯迴歸模型
model = LogisticRegression()
model.fit(x_train, y_train)
# 預測概率值(取正類的概率)
y_pred_proba = model.predict_proba(x_test)[:, 1]
# 計算AUC
auc_score = roc_auc_score(y_test, y_pred_proba)
print(auc_score)