Java 中的這個絕對值有點不絕對啊！詳情 - 後端,補碼,二進制,溢出用户bPbhIAe 博客

現象

假如有如下代碼定義了一個方法 test()，它入參可以任何一個 int 類型的整數，那麼它輸出結果可能是什麼？

public class Test {  
    public static void test(int a) {  
        System.out.println("The result of absolute value compare to zero is:" + (Math.abs(a) >= 0));  
    }  
}

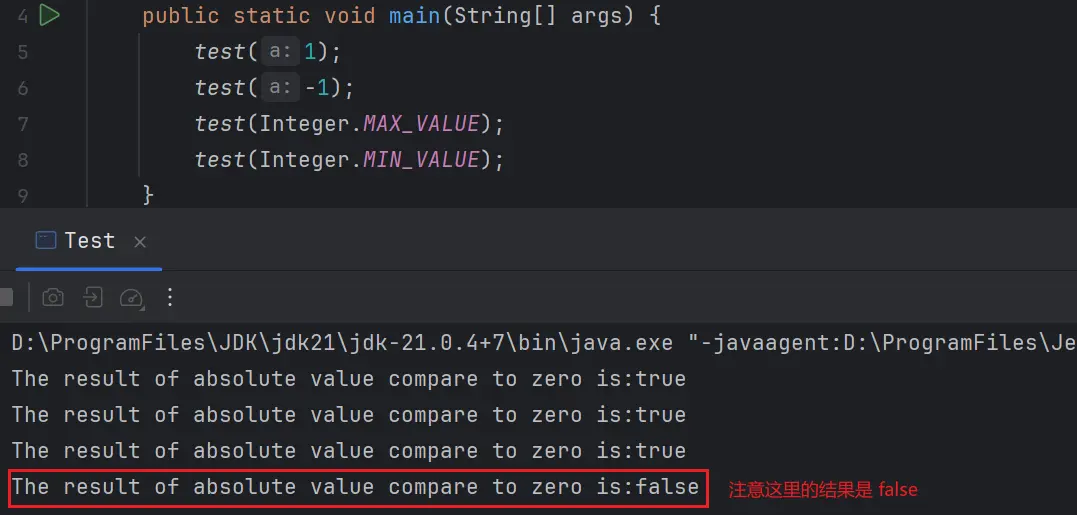
如果你的結論是 true，那麼恭喜你，你掉入到絕對值不絕對的坑裏面了。這個方法輸出的結果有可能是 true，但是也有可能是 false。比如下面的調用代碼將分別輸出 true，true，true , false，如下圖所示：

public static void main(String[] args) {
    test(1);
    test(-1);
    test(Integer.MAX_VALUE);
    test(Integer.MIN_VALUE);
}

在 Java 中，通過 Math.abs() 函數返回的值有的時候並不是這個數的絕對值。如下面的代碼所示：

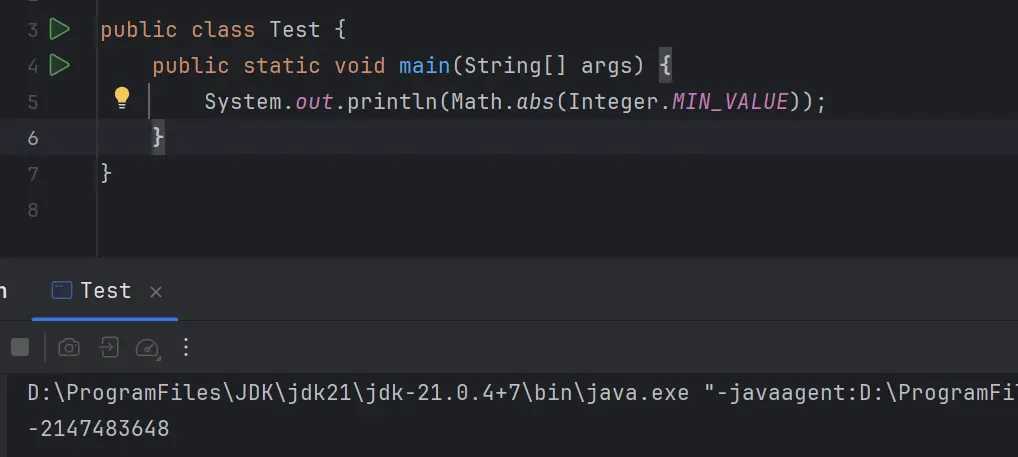
public static void main(String[] args) {
    System.out.println(Math.abs(Integer.MIN_VALUE));
}

上面的代碼輸出的結果並不是 Integer.MIN_VALUE 的絕對值，輸出的結果是它自己，如下圖所示：

從輸出可以看到因為 Math.abs(Integer.MIN_VALUE) 的結果還是 Integer.MIN_VALUE，因此它是小於 0 的，這個也解釋了上面判斷大於等於 0 結果有可能輸出的是 false。

為什麼 Math.abs(Integer.MIN_VALUE) 的結果還是 Integer.MIN_VALUE 而不是它的絕對值呢？

原理

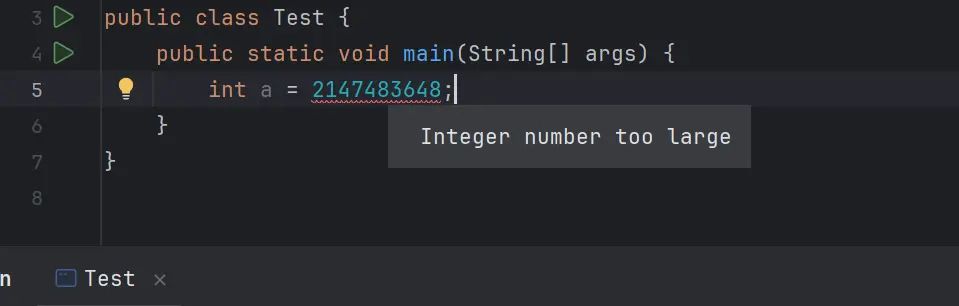
從 int 類型可以表示的數的範圍解釋是比較好理解的。以 int 類型為例，它能夠表示的範圍是 2^31 到 2^31 - 1。即 -2147483648 到 2147483647，可以看到最小的負數是 -2147483648 。它的絕對值實際上應該是 2147483648，但是這個值已經超過了 int 類型能夠表示的最大的數 2147483647 了。如果返回 2147483648，它是不能在一個 int 類型的數中表示的。如果我們直接把 2147483648 這個數賦值給一個 int 類型的變量，編譯器也會提示 Integer number too large，如下圖所示：

因此這裏 Math.abs() 函數返回的結果並不能是 214748364，因為 int 類型根本表示不了這個數。

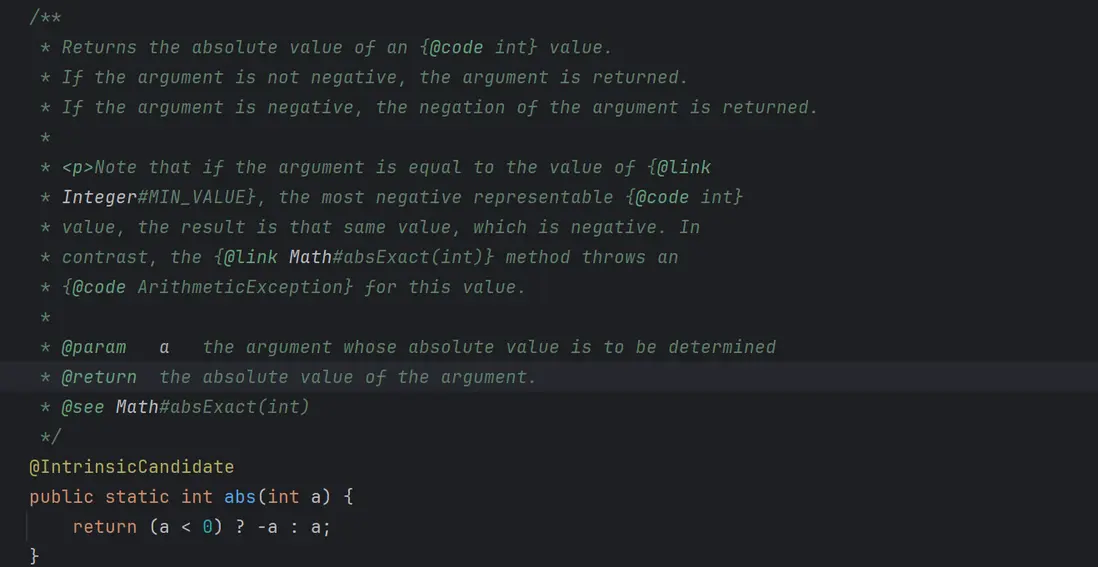
那 Math.abs() 方法做了什麼操作呢？查看 Math.abs() 方法的源碼，實現邏輯如下：

在方法中就是判斷了一下這個數是否小於 0，如果小於 0 的話，就返回對這個數取反後的值。那這個取反操作具體做了什麼事情呢？為什麼對 Integer.MIN_VALUE 進行了求反操作返回的還是它自己？

要回答這些問題，那就得知道計算機底層是表示一個整數的方式以及 int 類型表示的數的範圍是 2^31 到 2^31 - 1 的原因。

Java語言規範中對此做了描述，規範中説到 Java 語言中使用「two's-complement representation」來表示整數，因為「two's-complement representation」的值不是對稱的，所以對 int 或者 long 類型的最小值的取反的結果還是它們自身，在這個場景是有「溢出」發生的。而對一個整數的取反操作相當於把它的所有比特位取反，然後再加上 1。如下圖所示：

規範這裏的提到的「two's-complement」就是我們常常説的「補碼」，學過計算機組成原理相關課程的應該對這個詞語比較耳熟。

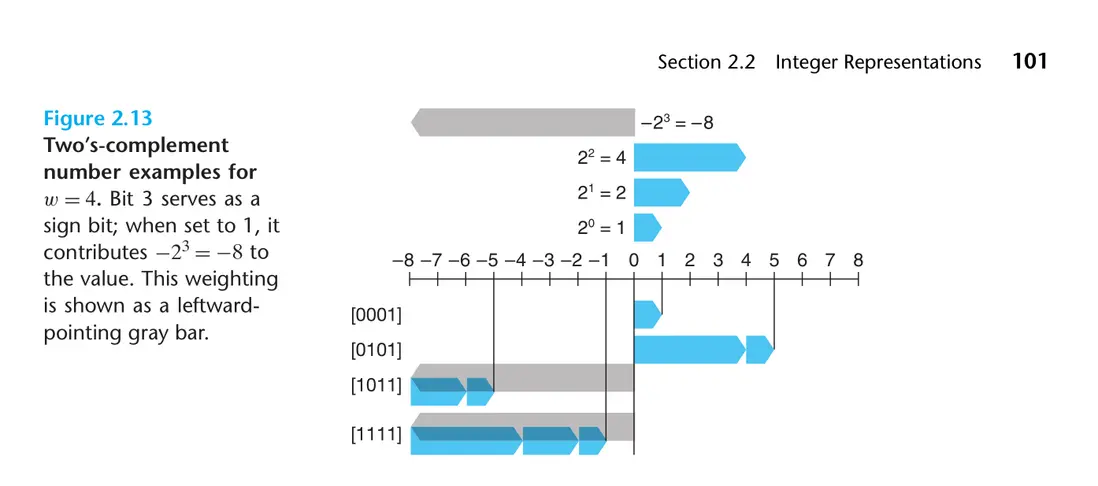
補碼就是將二進制位的最高位作為符號位，它的權重是 -2^(w -1) （這裏的 w 為比特位的個數），如果它設置為 1 表示負數，如果設置為 0，表示非負數。如下圖所示：

根據補碼的定義來看，補碼能夠表示的最大的數是 2^(w -1) - 1，而它能夠表示的最小的的數是 -2^(w -1) （這裏的 w 為比特位的個數）。那麼最小數的絕對值是比最大數的絕對值還要大 1 的。從上面的圖也可以看出（上圖中的比特位數為 4），數軸最左側的刻度是 -8，而數軸最右側的刻度是 7。

對於補碼的取反操作是把每個比特位都取反，然後加上 1。為什麼補碼的取反要這樣操作？從數學的角度上講一個數 x 加上它的取反 -x 的結果應該是 0。從計算機的角度我們可以知道 x 加上 x 的每個比特位取反的結果是每個比特位都是 1，按照補碼的表示方式就是 10 進制的 -1，然後再加上 1 那就是 0，這樣的結果就和數學上是相符合的了。比如假設總的比特位數是 8，1 的補碼是 0000_0001，取反之後就是 1111_1110，相加的結果是 1111_1111，即 -1，然後加上 1 就是 0000_0000，即 0。如下圖所示：

補碼的英文名字「 two's complement」這個名字的由來是如果把一個數的補碼和它取反的補碼得到的二進制都看作是無符號數的話，它相加的結果就是 2^w （這裏的 w 為比特位的個數）。如下圖所示：

回過頭來看 Java 中的 int 類型，它的最小值 Integer.MIN_VALUE 的補碼錶示形式就是 1000_0000_0000_0000_0000_0000_0000_0000，按照補碼取反操作的規則，應該是把它的補碼按位取反得到 0111_1111_1111_1111_1111_1111_1111_1111，然後加 1，得到的結果還是 1000_0000_0000_0000_0000_0000_0000_0000，即它自己。因此在 Math.abs() 函數中對 Integer.MIN_VALUE 取反後得到的值仍然是 Integer.MIN_VALUE。

解決方法

對於 Integer.MIN_VALUE 的絕對值溢出現象的解決方法有以下幾種：

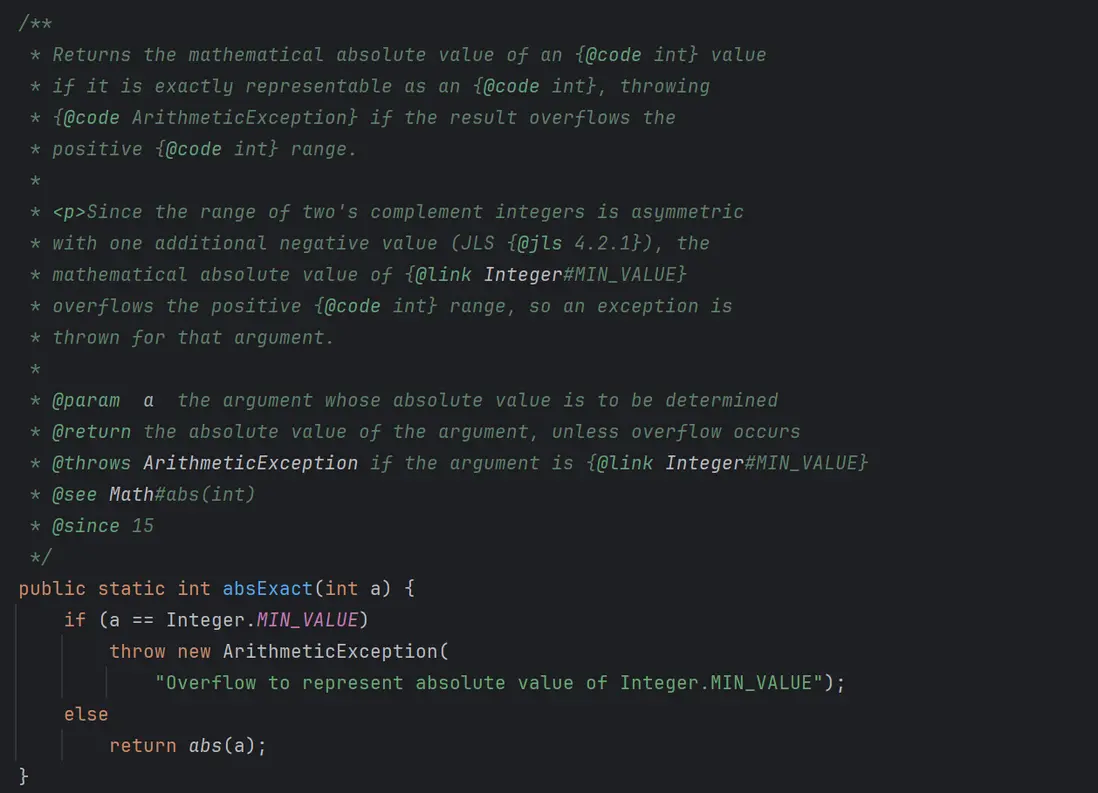
一種是使用 Math.absExact() 方法，該方法在獲取絕對值之前會判斷是否超過了表示範圍，如果超過了表示範圍會拋出一個異常，如下圖所示：

public class Test {  
    public static void main(String[] args) {  
        System.out.println(Math.absExact(Integer.MIN_VALUE));  
    }  
}

實現原理其實就是在進入方法時判斷了一下是否是 Integer.MIN_VALUE ，如果是就直接拋出異常了，如下圖所示：

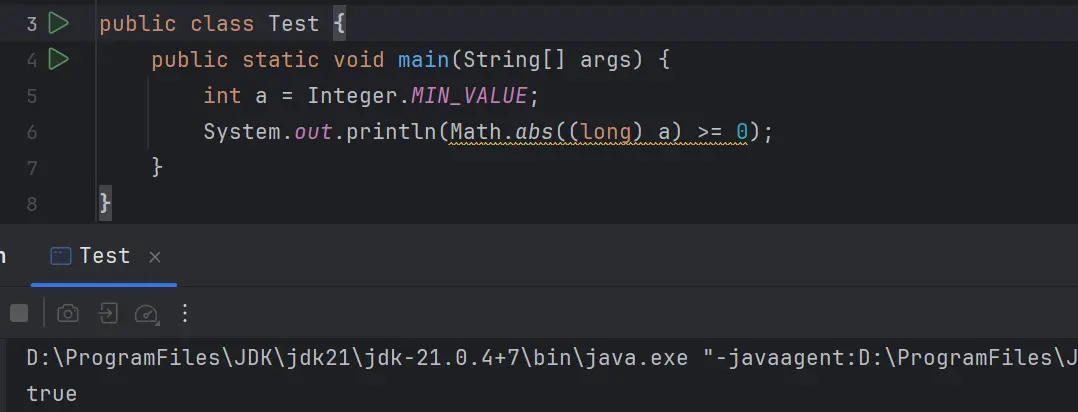
也可以轉為 long 類型後再獲取絕對值，因為 Integer.MIN_VALUE 的絕對值是可以用 long 類型來表示的，因此轉為 long 類型來獲取絕對值也是可以的，但是這個方法就解決不了 Long.MIN_VALUE 絕對值溢出現象。如下圖所示：

public static void main(String[] args) {  
    int a = Integer.MIN_VALUE;  
    System.out.println(Math.abs((long) a) >= 0);  
}

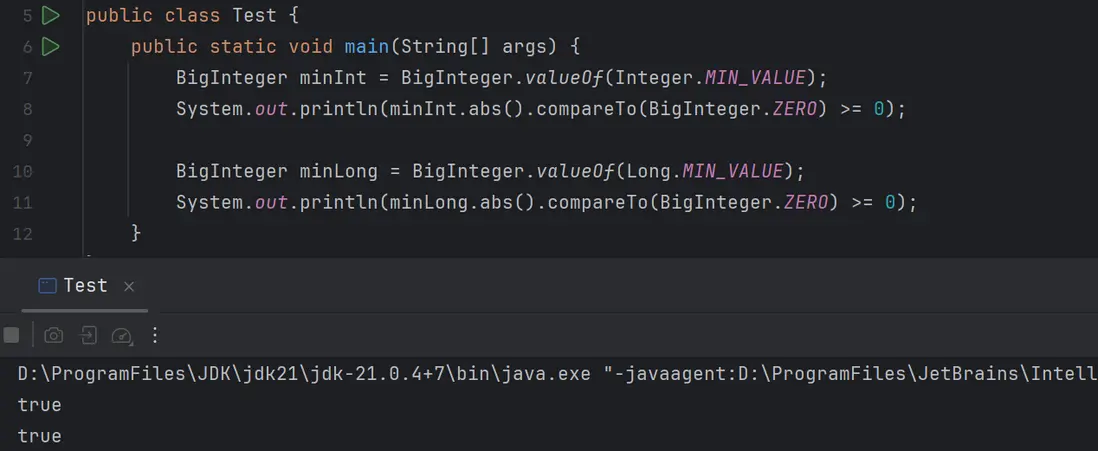
還有一種可以使用 Integer.MIN_VALUE 構造一個 BigInteger 對象，然後通過獲取這個對象的絕對值來和 BigDecimal.ZERO 來比較，這種方式不僅可以解決 Integer.MIN_VALUE 的絕對值溢出問題，還可以解決 Long.MIN_VALUE 的絕對值溢出問題。如下面的代碼：

public static void main(String[] args) {  
    BigInteger minInt = BigInteger.valueOf(Integer.MIN_VALUE);  
    System.out.println(minInt.abs().compareTo(BigInteger.ZERO) >= 0);  
  
    BigInteger minLong = BigInteger.valueOf(Long.MIN_VALUE);  
    System.out.println(minLong.abs().compareTo(BigInteger.ZERO) >= 0);  
}

參考

Unary Minus Operator
Sign–magnitude
Ones' complement
Two's_complement
二進制—原碼、反碼、補碼
Computer Organization and Design
Computer Systems: A Programmer's Perspective

用户bPbhIAe 博客

用户bPbhIAe 博客

博客 / 詳情