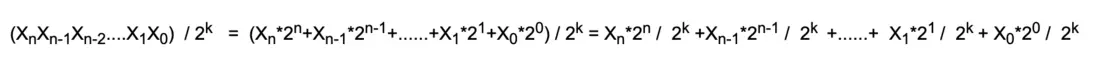文章目錄:
①、拋出問題
②、給出結論
③、論證問題
④、& 和 % 運算效率對比
相信對 JDK 源碼感興趣的小夥伴,HashMap 的源碼你一定不要錯過,裏面有很多精妙的設計,也是面試的常用考點,本文我會點出一些。
但是我不詳細介紹 HashMap 源碼,想了解的可以看我之前的文章,本篇文章主要是給大家解惑幾個問題。
1、拋出問題
1.1 為什麼 HashMap 的默認初始容量長度要是 1<<4 ?
為啥源碼這裏不直接寫 16 ?要寫成 1<<4?知道的可以在評論區留言。
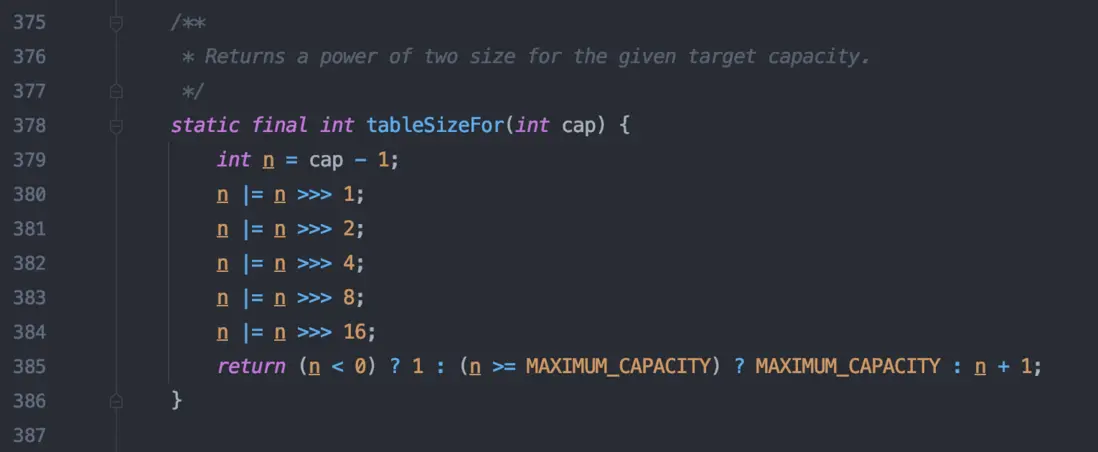
1.2 為什麼 HashMap 初始化即使給定長度,依然要重新計算一個 2^n^ 的數?
PS: 這個方法是 HashMap 用於計算初始化容量,結果是返回大於給定值的第一個偶數,比如 :
new HashMap(10),其實實際長度是 16;
new HashMap(18),實際長度是32;
new HashMap(40),實際長度64。
涉及到兩個運算符:
①、| : 或運算符。
②、>>> : 無符號右移運算符,移動時忽略符號位,空位以 0 補齊。
這個算法也比較有意思,原理就是每一次運算都是將現有的 0 的位轉換成 1,直到所有的位都為 1 為止;最後返回結果的時候,如果比最大值小,則返回結果+1,正好將所有的 1 轉換成 0,且進了一位,剛好是 2^n^ 。
1.3 為什麼 HashMap 每次擴容是擴大一倍,也就是 2^1^ ?
當存入HashMap的元素佔比超過整個容量的75%(默認加載因子 DEFAULT_LOAD_FACTOR = 0.75)時,進行擴容,而且在不超過int類型的範圍時,左移1位(長度擴為原來2倍)
1.4 為什麼 HashMap 的計算索引算法是 &,而不是 % ?
新添加一個元素時,會計算這個元素在 HashMap 中的位置,算法分為兩步:
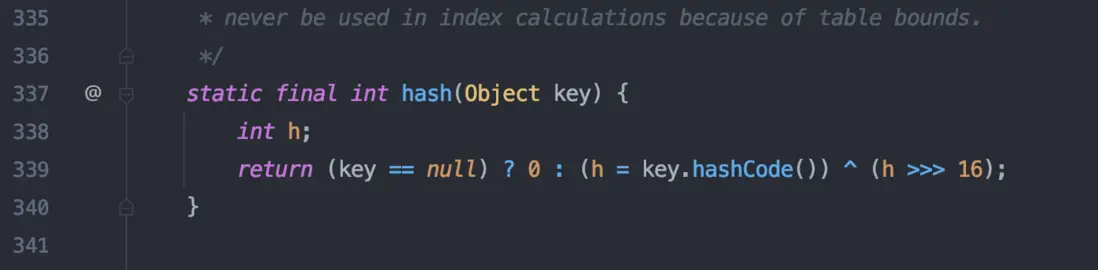
①、得到 hash 值
PS:其實這裏的算法可以研究下,hashcode() 是一個 native 修飾的方法,返回一個 int 類型的值(根據內存地址換算出來的一個值),然後將這個值無符號右移16位,高位補0,並與前面第一步獲得的hash碼進行按位異或^ 運算。
這樣做有什麼用呢?這其實是一個擾動函數,為了降低哈希碼的衝突。右位移16位,正好是32bit的一半,高半區和低半區做異或,就是為了混合原始哈希碼的高位和低位,以此來加大低位的隨機性。
這樣混合後的低位摻雜了高位的部分特徵,高位的信息也被變相保留下來。
也就是保證考慮到高低Bit位都參與到Hash的計算中。
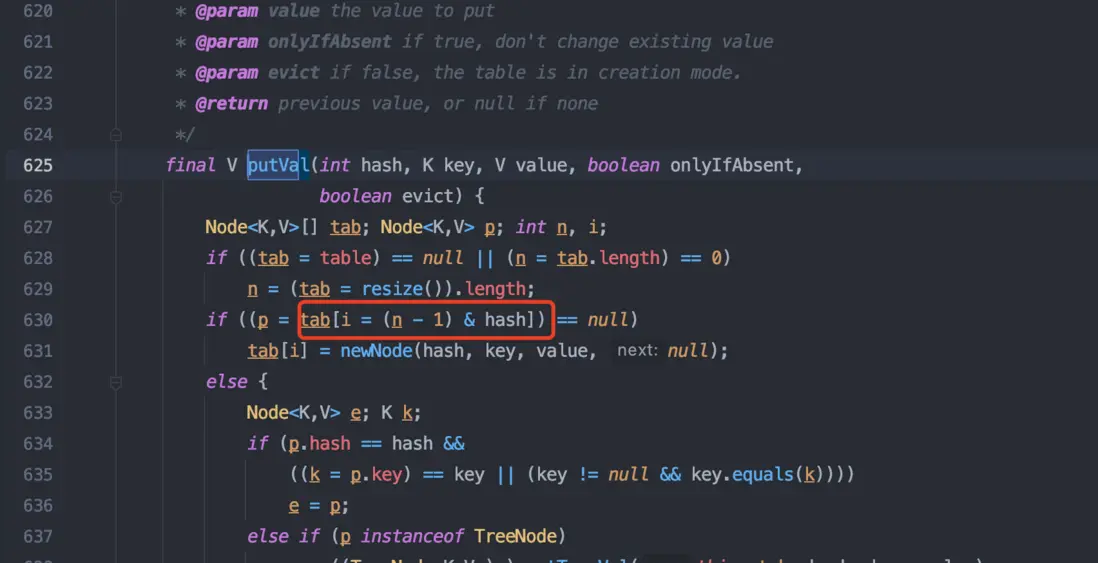
②、索引值 i = (n-1) & hash
這裏的 n 是 HashMap 的長度,hash 是上一步得到的值。
注意:這裏是用的按位與 & ,而不是用的取模 %。
1.5 問題總結
大家發現沒,通過我上面提出的四個問題,前三個問題 HashMap 的長度始終保持在 2^n^ 。
①、默認初始長度是 2^4^;
②、即使給定初始長度,其值依舊是大於給定值的第一個偶數;
③、每次擴容都是擴大一倍,2^1^;
然後第四個問題,計算 HashMap 的元素索引時,我們得到了一個 hash 值,居然是對 HashMap 的長度做 & 運算,而不是做 % 運算,這到底是是為什麼呢?
2、給出結論
我們先直接給出結論:
當 lenth = 2^n^ 且X>0 時,X % length = X & (length - 1)
也就是説,長度為2的n次冪時,模運算 % 可以變換為按位與 & 運算。
比如:9 % 4 = 1,9的二進制是 1001 ,4-1 = 3,3的二進制是 0011。 9 & 3 = 1001 & 0011 = 0001 = 1
再比如:12 % 8 = 4,12的二進制是 1100,8-1 = 7,7的二進制是 0111。12 & 7 = 1100 & 0111 = 0100 = 4
上面兩個例子4和8都是2的n次冪,結論是成立的,那麼當長度不為2的n次冪呢?
比如:9 % 5 = 4,9的二進制是 1001,5-1 = 4,4的二進制是0100。9 & 4 = 1001 & 0100 = 0000 = 0。顯然是不成立的。
為什麼是這樣?下面我們來詳細分析。
3、論證結論
首先我們要知道如下規則:
①、"<<" 左移:按二進制形式把所有的數字向左移動對應的位數,高位移出(捨棄),低位的空位補零。左移一位其值相當於乘2。
②、">>"右移:按二進制形式把所有的數字向右移動對應的位數。對於左邊移出的空位,如果是正數則空位補0,若為負數,可能補0或補1,這取決於所用的計算機系統。右移一位其值相當於除以2。
③、">>>"無符號右移:右邊的位被擠掉,對於左邊移出的空位一概補上0。
根據二進制數的特點,相信大家很好理解。
現在對於給定一個任意的十進制數X~n~X~n-1~X~n-2~....X~1~X~0~,我們將其用二進制的表示方法分解:
公式1:
X~n~X~n-1~X~n-2~....X~1~X~0~ = X~n~2^n^+X~n-1~2^n-1^+......+X~1~2^1^+X~0~2^0^
回到上面的結論:當 lenth = 2^n^ 且X>0 時,X % length = X & (length - 1)
以及對於除法,除以一個數能用除法分配律,除以幾個數的和或差不能用除法分配律:
公式2:
成立:(a+b)÷c=a÷c+b÷c
不成立:a÷(b+c)≠a÷c+a÷c
通過 公式1以及 公式2,我們可以得出當任意一個十進制除以一個2^k^的數時,我們可以將這個十進制轉換成公式1的表示形式:
如果我們想求上面公式的餘數,相信大家一眼就能看出來:
①、當 0<= k <= n 時,餘數為 X~k~2^k^+X~k-1~2^k-1^+......+X~1~2^1^+X~0~2^0^ ,也就是説 比 k 大的 n次冪,我們都舍掉了(大的都能整除 2^k^),比k小的我們都留下來了(小的不能整除2^k^)。那麼留來下來即為餘數。
②、當 k > n 時,餘數即為整個十進制數。
看到這裏,我們離證明結論已經很近了。
再回到上面説的二進制的移位操作,向右移 n 位,表示除以 2^n^ 次方,由此我們得到一個很重要的結論:
一個十進制數對一個2^n^ 的數取餘,我們可以將這個十進制轉換為二進制數,將這個二進制數右移n位,移掉的這 n 位數即是餘數。
知道怎麼算餘數了,那麼我們怎麼去獲取這移掉的 n 為數呢?
我們再看2^0^,2^1^,2^2^....2^n^ 用二進制表示如下:
0001,0010,0100,1000,10000......
我們把上面的數字減一:
0000,0001,0011,0111,01111......
根據與運算符&的規律,當位上都是 1 時,結果才是 1,否則為 0。所以任意一個二進制數對 2^k^ 取餘時,我們可以將這個二進制數與(2^k^-1)進行按位與運算,保留的即是餘數。
這就完美的證明了前面給出的結論:
當 lenth = 2^n^ 且X>0 時,X % length = X & (length - 1)
4、& 和 % 運算效率
為什麼要將 % 運算改為 & 運算,很顯然是因為 & 運算在計算機底層只需要一個簡單的 與邏輯門就可以實現,但是實現除法確實一個很複雜的電路,大家感興趣的可以下去研究下。
我這裏在代碼層面,給大家做個測試,直觀的比較下速度:
public class HashMapTest {
public static void main(String[] args) {
long num = 100000*100000;
long startTimeMillis1 = System.currentTimeMillis();
long result = 1;
for (long i = 1; i < num; i++) {
result %= i;
}
long endTimeMillis1 = System.currentTimeMillis();
System.out.println("%: "+ (endTimeMillis1 - startTimeMillis1));
long startTimeMillis2 = System.currentTimeMillis();
result = 1;
for (long i = 1; i < num; i++) {
result &= i;
}
long endTimeMillis2 = System.currentTimeMillis();
System.out.println("&: "+ (endTimeMillis2 - startTimeMillis2));
}
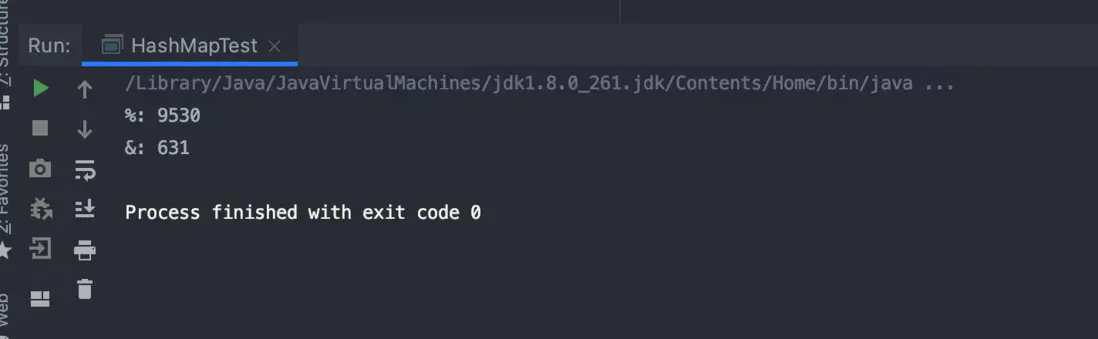
}打印結果如下:
差距還是很明顯的,而且這個結果還會隨着測試次數的增多而越拉越開。