一、題目大意

給定一個二叉搜索樹的根節點 root 和一個值 key，刪除二叉搜索樹中的 key 對應的節點，並保證二叉搜索樹的性質不變。返回二叉搜索樹（有可能被更新）的根節點的引用。

一般來説，刪除節點可分為兩個步驟：

• 首先找到需要刪除的節點；
• 如果找到了，刪除它。

示例 1:

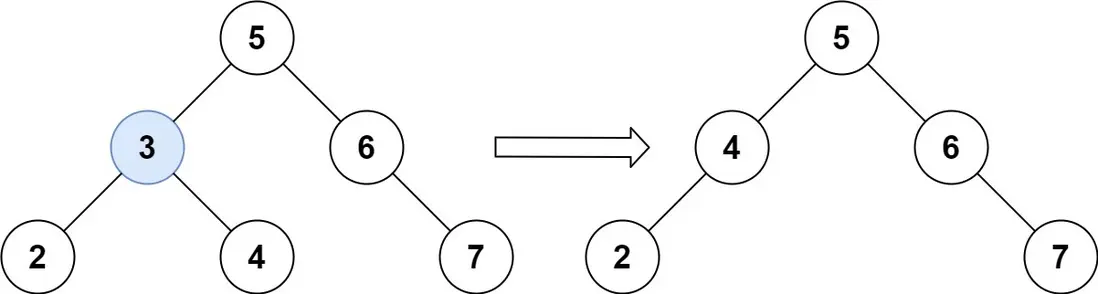
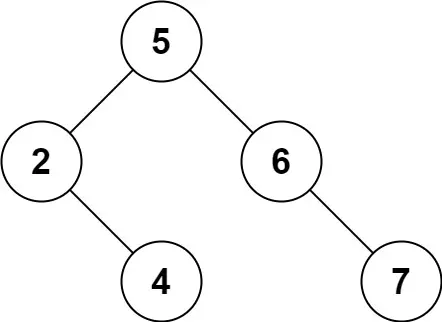
輸入：root = [5,3,6,2,4,null,7], key = 3

輸出：[5,4,6,2,null,null,7]

解釋：給定需要刪除的節點值是 3，所以我們首先找到 3 這個節點，然後刪除它。

一個正確的答案是 [5,4,6,2,null,null,7], 如下圖所示。

另一個正確答案是 [5,2,6,null,4,null,7]。

示例 2:

輸入: root = [5,3,6,2,4,null,7], key = 0

輸出: [5,3,6,2,4,null,7]

解釋: 二叉樹不包含值為 0 的節點

示例 3:

輸入: root = [], key = 0

輸出: []

提示:

• 節點數的範圍 [0, 104].
• -105 <= Node.val <= 105
• 節點值唯一
• root 是合法的二叉搜索樹
• -105 <= key <= 105

來源：力扣（LeetCode）
鏈接：https://leetcode.cn/problems/...
著作權歸領釦網絡所有。商業轉載請聯繫官方授權，非商業轉載請註明出處。

二、解題思路

這道題讓我們刪除二叉搜索樹中的一個節點，難點在於刪除完節點並補上那個節點的位置後還應該是一棵二叉搜索樹。被刪除掉的節點位置，不一定是由其左右節點補上，

         7
        / \
       4   8
     /   \   
    2     6
     \   /
      3 5

上面這棵樹，如果要刪除節點4，那麼應該將節點5補到4的位置，這樣才能保證還是BST，結果是下面這棵樹

         7
        / \
       5   8
     /   \   
    2     6
     \   
      3

遞歸思路：首先判斷根節點是否為空，由於BST的性質：左 < 根 < 右，使得可以快速定位到要刪除的節點，對於當前節點值不等於key的情況，根據大小關係對其左右子節點分別調用遞歸函數。若當前節點就是要刪除的節點，先判斷若有一個子節點不存在，就將root指向另一個節點，如果左右節點都不存在，那麼root就賦值為空了，也正確。難點就在於處理左右子節點都存在的情況，需要在右子樹找到最濉址，即右子樹中最左下方的節點，然後將該最小值賦值給root，然後再在右子樹中調用遞歸函數來mbmw這個最小的節點。

三、解題方法

3.1 Java實現

public class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        if (root.val > key) {
            root.left = deleteNode(root.left, key);
        } else if (root.val < key) {
            root.right = deleteNode(root.right, key);
        } else {
            if (root.left == null || root.right == null) {
                root = (root.left != null) ? root.left : root.right;
            } else {
                TreeNode cur = root.right;
                while (cur.left != null) {
                    cur = cur.left;
                }
                root.val = cur.val;
                root.right = deleteNode(root.right, cur.val);
            }
        }
        return root;
    }
}

四、總結小記

• 2022/10/21 腦力勞動的人更容易摸魚