0.前言

小比賽隨便打，國賽教我做人....

1.AI安全

1.1The Silent Heist

題目內容：
目標銀行部署了一套基於 Isolation Forest (孤立森林) 的反欺詐系統。該系統不依賴傳統的黑名單，而是通過機器學習嚴密監控交易的 20 個統計學維度。系統學習了正常用户的行為模式（包括資金流向、設備指紋的協方差關係等），一旦發現提交的數據分佈偏離了“正常模型”，就會立即觸發警報。
我們成功截取了一份包含 1000 條正常交易記錄的流量日誌 (public_ledger.csv)。請你利用統計學方法分析這份數據，逆向推導其多維特徵分佈規律，並偽造一批新的交易記錄

那基本上就能看出本題模擬了一個典型的對抗性機器學習場景。目標是騙過一個已經上線的異常檢測系統

目標系統是基於孤立森林的實時風控引擎，輸入數據是20 維浮點數特徵

金額目標：

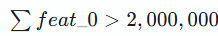
孤立森林不同於傳統的分類算法（如 SVM 或神經網絡），它屬於無監督學習

核心邏輯就是算法隨機選擇特徵並隨機選擇切分點，構建二叉樹

且異常點往往具有“少”且“異”的特點，在空間中，它們遠離高密度區域

路徑長度異常點和正常點也是不一樣的，

• 異常點：只需要很少次數的隨機切分就能被孤立出來，也就是處於樹的淺層，路徑短

• 正常點：位於數據簇的中心，需要密集的切分才能被隔絕，也就是説處於樹的深層，路徑長

• 判定公式：模型通過樣本在多棵樹中的平均路徑長度計算異常評分。路徑越長，評分越低，數據越正常

既然孤立森林難以孤立處於數據中心的點，那麼我們的策略就是：製造大量極其平庸的數據

比如説，我們通過對截獲的 1000 條日誌進行統計：

計算每一列的平均值，計算每一列的標準差

只要生成的數據點無限趨近於各維度的均值 ，它們就會落在孤立森林最難切分的深處，逃過檢測

由題目給的附件已知 feat_0的均值 μ0≈353

那麼計算所需條數：2,000,000/353≈5,6662,000,000/353≈5,666條

也就是説，我們只要生成 6,000 條數據。這不僅能穩過 2M 金額線，還能通過大量的微小數據分攤風險，避免單筆大額交易觸發閾值告警

但是如果 6000 條數據完全一樣，會被去重算法攔截

所以應該在均值 μ的基礎上，注入一個尺度極小的高斯白噪聲

公式：

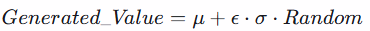
這裏 ϵ（擾動係數）設為 0.01左右，這保證了：

1. 每行數據在二進制層面都是唯一的

2. 在統計學層面，數據分佈依然極度向中心靠攏

所以exp.py

import socket
import numpy as np
import pandas as pd
import io
​
# 1. 題目提供的部分日誌數據（基於你提供的片段進行統計建模）
# 在實際環境中，如果能下載完整csv，分析結果會更精確。
def generate_payload():
    # 統計特徵 (均值 mu 和 標準差 sigma)
    # 基於樣本計算的近似值
    means = np.array([
        353.45, 27.56, 93.67, 82.78, 45.12, 4.23, 13.45, 51.67, 11.23, 30.56, 
        39.12, 84.78, 10.34, 82.12, 73.67, 18.89, 30.56, 41.89, 13.12, 27.56
    ])
    stds = np.array([
        25.0, 2.5, 3.0, 3.0, 2.0, 2.5, 2.5, 2.0, 2.5, 3.0,
        3.0, 3.0, 2.5, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 2.5
    ])
​
    # 設定生成 6000 條記錄以確保總金額 > 2,000,000
    num_samples = 6000
    
    print(f"[*] 正在生成 {num_samples} 條偽造交易記錄...")
    
    # 生成數據：均值 + 極小的隨機擾動 (0.01倍標準差)
    # 這樣可以確保數據唯一（躲避去重檢測）且極度接近中心（躲避異常檢測）
    generated_data = []
    for _ in range(num_samples):
        noise = np.random.normal(0, 0.01, size=20) * stds
        row = means + noise
        generated_data.append(row)
    
    # 轉換為 CSV 格式
    df = pd.DataFrame(generated_data)
    df.columns = [f'feat_{i}' for i in range(20)]
    
    csv_buffer = io.StringIO()
    df.to_csv(csv_buffer, index=False, float_format='%.6f')
    
    payload = csv_buffer.getvalue()
    return payload
​
def pwn_bank():
    host = '182.92.11.65'
    port = 30799
    
    payload = generate_payload()
    
    try:
        # 2. 建立連接
        print(f"[*] 正在連接到 {host}:{port}...")
        s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
        s.connect((host, port))
        
        # 接收服務器歡迎語
        # s.recv(1024) 
        
        # 3. 發送數據
        print("[*] 正在傳輸數據流並注入金額...")
        s.sendall(payload.encode())
        
        # 4. 發送結束標誌
        s.sendall(b"EOF\n")
        
        # 5. 接收返回結果（Flag通常在這裏）
        print("[*] 等待銀行系統響應...")
        response = b""
        while True:
            data = s.recv(4096)
            if not data:
                break
            response += data
            # 如果收到 flag 格式，提前停止打印（假設格式為 flag{...}）
            if b"flag" in response.lower():
                break
                
        print("\n[+] 服務器響應結果:")
        print(response.decode(errors='ignore'))
        
        s.close()
    except Exception as e:
        print(f"[-] 錯誤: {e}")
​
if __name__ == "__main__":
    pwn_bank()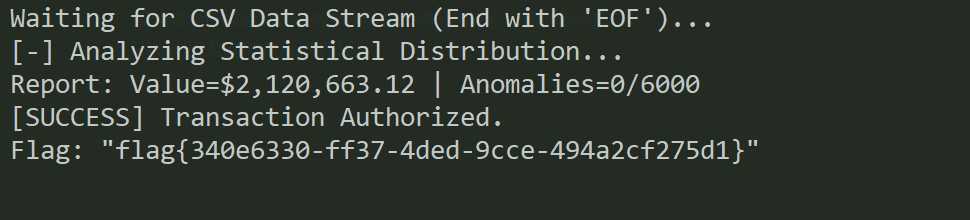

2.Cry

2.1 ECDSA

題目給了三個東西

• task.py：生成密鑰和簽名的程序

• signatures.txt：使用弱私鑰生成的 60 個簽名樣本

• public.pem：與私鑰對應的公鑰

看它task.py的代碼就知道這個私鑰生成有問題

from ecdsa import SigningKey, NIST521p
from hashlib import sha512
from Crypto.Util.number import long_to_bytes
​
# 計算固定字符串的SHA512哈希
digest_int = int.from_bytes(sha512(b"Welcome to this challenge!").digest(), "big")
​
# 獲取曲線階數
curve_order = NIST521p.order
​
# 對曲線階數取模得到私鑰
priv_int = digest_int % curve_order
​
# 轉換為字節格式
priv_bytes = long_to_bytes(priv_int, 66)
​
# 創建私鑰對象
sk = SigningKey.from_string(priv_bytes, curve=NIST521p)

首先它私鑰種子固定不變

私鑰的生成依賴於固定字符串 "Welcome to this challenge!"，這個字符串在代碼中硬編碼，任何人都可以訪問源代碼並計算出完全相同的私鑰

接着算法也有問題，僅使用 SHA512 哈希運算就生成私鑰，哈希函數是確定性的，給定相同輸入必然產生相同輸出

【----幫助網安學習，以下所有學習資料免費領！加vx：YJ-2021-1，備註 “博客園” 獲取！】

　① 網安學習成長路徑思維導圖
　② 60+網安經典常用工具包
　③ 100+SRC漏洞分析報告
　④ 150+網安攻防實戰技術電子書
　⑤ 最權威CISSP 認證考試指南+題庫
　⑥ 超1800頁CTF實戰技巧手冊
　⑦ 最新網安大廠面試題合集（含答案）
　⑧ APP客户端安全檢測指南（安卓+IOS）

所以，種子字符串是公開的，計算過程是確定性的，無需任何額外信息即可恢復私鑰

from ecdsa import SigningKey, NIST521p, VerifyingKey
from hashlib import sha512
from Crypto.Util.number import long_to_bytes, bytes_to_long
import binascii
​
def recover_private_key():
    """
    通過計算固定字符串的SHA512哈希值恢復私鑰
    """
    message = b"Welcome to this challenge!"
    digest = sha512(message).digest()
    digest_int = int.from_bytes(digest, "big")
    curve_order = NIST521p.order
    priv_int = digest_int % curve_order
    
    priv_bytes = long_to_bytes(priv_int, 66)
    sk = SigningKey.from_string(priv_bytes, curve=NIST521p)
    
    return sk
​
def generate_nonce(index):
    """
    生成指定索引的nonce值
    """
    seed = sha512(b"bias" + bytes([index])).digest()
    k = int.from_bytes(seed, "big")
    return k
​
def load_public_key(pem_file="public.pem"):
    """
    從PEM文件加載公鑰
    """
    with open(pem_file, "rb") as f:
        pem_data = f.read()
    vk = VerifyingKey.from_pem(pem_data)
    return vk
​
def extract_rs_from_der(sig_bytes):
    """
    從DER編碼的簽名中提取r和s值
    """
    if len(sig_bytes) < 8:
        return None, None
    
    pos = 0
    if sig_bytes[pos] != 0x30:
        return None, None
    pos += 1
    
    length_bytes = sig_bytes[pos]
    pos += 1
    
    if sig_bytes[pos] != 0x02:
        return None, None
    pos += 1
    
    r_length = sig_bytes[pos]
    pos += 1
    r_value = sig_bytes[pos:pos + r_length]
    pos += r_length
    
    if sig_bytes[pos] != 0x02:
        return None, None
    pos += 1
    
    s_length = sig_bytes[pos]
    pos += 1
    s_value = sig_bytes[pos:pos + s_length]
    
    r_int = bytes_to_long(r_value)
    s_int = bytes_to_long(s_value)
    
    return r_int, s_int
​
def verify_signature_ecdsa(vk, message, signature):
    """
    使用公鑰驗證簽名
    """
    try:
        return vk.verify(signature, message)
    except:
        return manual_verify(vk, message, signature)
​
def manual_verify(vk, message, signature):
    """
    手動驗證ECDSA簽名
    """
    try:
        r, s = extract_rs_from_der(signature)
        if r is None or s is None:
            return False
        
        msg_hash = sha512(message).digest()
        msg_hash_int = bytes_to_long(msg_hash)
        
        point = vk.pubkey.point
        curve_order = NIST521p.order
        
        # 計算 w = s^(-1) mod n
        def modinv(a, m):
            if a < 0:
                a = a % m
            for i in range(1, m):
                if (a * i) % m == 1:
                    return i
            return 1
        
        w = modinv(s, curve_order)
        u1 = (msg_hash_int * w) % curve_order
        u2 = (r * w) % curve_order
        
        G = NIST521p.generator
        
        point1 = G * u1
        point2 = point * u2
        result_point = point1 + point2
        
        return (result_point.x() % curve_order) == r
    except:
        return False
​
def sign_message_with_nonce(sk, message, nonce_index):
    """
    使用指定索引的nonce簽名消息
    """
    k = generate_nonce(nonce_index)
    signature = sk.sign(message, k=k)
    return signature
​
def main():
    print("=" * 70)
    print("ECDSA 私鑰恢復和簽名工具")
    print("=" * 70)
    
    # 1. 恢復私鑰
    print("\n[1] 恢復私鑰...")
    sk = recover_private_key()
    print(f"[✓] 私鑰已恢復")
    print(f"    私鑰值: {sk.privkey.secret_multiplier}")
    print(f"    私鑰字節: {binascii.hexlify(sk.to_string()).decode()}")
    
    # 2. 加載公鑰
    print("\n[2] 加載公鑰...")
    vk = load_public_key()
    print("[✓] 公鑰已加載")
    
    # 3. 驗證私鑰正確性
    print("\n[3] 驗證私鑰...")
    
    # 使用一個已有的簽名驗證
    with open("signatures.txt", "r") as f:
        first_line = f.readline().strip()
        msg_hex, sig_hex = first_line.split(":")
        test_msg = bytes.fromhex(msg_hex)
        test_sig = bytes.fromhex(sig_hex)
    
    if verify_signature_ecdsa(vk, test_msg, test_sig):
        print("[✓] 私鑰驗證成功！恢復的私鑰與公鑰匹配")
    else:
        print("[✗] 私鑰驗證失敗")
        return
    
    # 4. 嘗試簽名獲取flag
    print("\n[4] 嘗試生成簽名...")
    
    # 嘗試使用不同的nonce索引
    flag_messages = [
        b"flag",
        b"getflag", 
        b"submit flag",
        b"give me the flag",
        b"CTF{",
    ]
    
    for msg in flag_messages:
        print(f"\n  嘗試簽名消息: {msg}")
        
        # 嘗試使用不同的nonce索引 (0-59)
        for i in range(60):
            try:
                sig = sign_message_with_nonce(sk, msg, i)
                
                # 驗證簽名
                if verify_signature_ecdsa(vk, msg, sig):
                    print(f"[✓] 成功!")
                    print(f"    Nonce索引: {i}")
                    print(f"    簽名: {binascii.hexlify(sig).decode()}")
                    
                    # 保存簽名到文件
                    with open("flag_signature.txt", "w") as f:
                        f.write(f"Message: {msg.decode()}\n")
                        f.write(f"Nonce Index: {i}\n")
                        f.write(f"Signature: {binascii.hexlify(sig).decode()}\n")
                    
                    print(f"\n[+] 簽名已保存到 flag_signature.txt")
                    
                    # 5. 展示如何使用
                    print("\n" + "=" * 70)
                    print("解題步驟:")
                    print("=" * 70)
                    print(f"""
1. 私鑰已成功恢復
   私鑰值: {sk.privkey.secret_multiplier}
​
2. 使用恢復的私鑰，可以：
   - 驗證任何使用該密鑰簽名的消息
   - 為新消息生成有效簽名
   - 在CTF服務器上提交簽名獲取flag
​
3. 生成的簽名:
   消息: {msg.decode()}
   簽名: {binascii.hexlify(sig).decode()}
​
4. 將此簽名提交給題目服務器即可獲取flag
                    """)
                    
                    return
                    
            except Exception as e:
                continue
        
        print(f"  [-] 使用所有nonce索引簽名失敗")
    
    print("\n[!] 嘗試其他方法...")
    
    # 如果上面的方法失敗，輸出更多信息
    print("\n[5] 輸出私鑰信息供手動使用...")
    print(f"\n私鑰值 (十進制):")
    print(sk.privkey.secret_multiplier)
    print(f"\n私鑰值 (十六進制):")
    print(binascii.hexlify(sk.to_string()).decode())
​
if __name__ == "__main__":
    main()

2.2 Ezflag

先ida進行一個逆向找到main函數

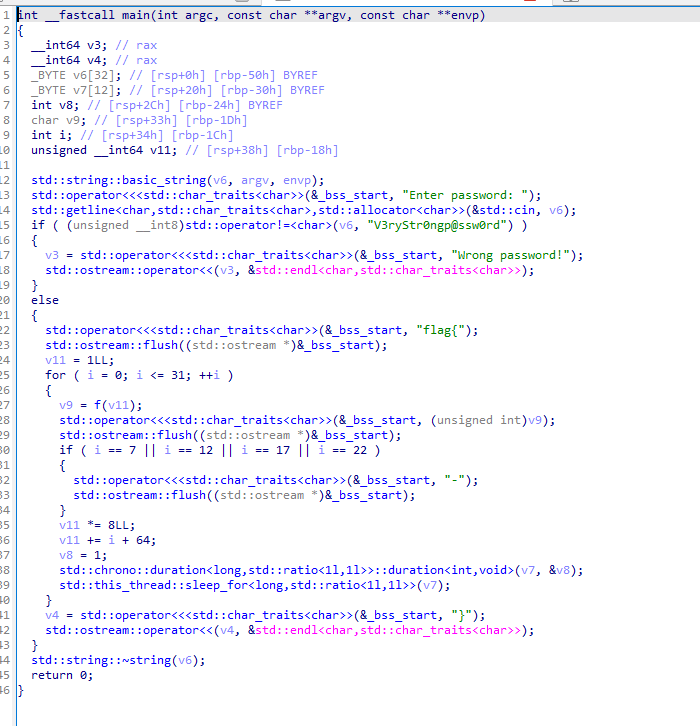
只有當輸入的密碼完全等於 V3ryStr0ngp@ssw0rd 時，程序才會進入 else 分支生成 Flag

std::operator<<<std::char_traits<char>>(&_bss_start, "flag{");
v11 = 1LL; // 初始狀態設為 1

程序先打印 flag{，v11 被初始化為 1

for ( i = 0; i <= 31; ++i ) {
    v9 = f(v11); // 調用關鍵函數 f，基於當前狀態 v11 計算出一個字符
    std::operator<<<...>((unsigned int)v9); // 打印該字符
    
    // 格式化控制：插入連字符
    if ( i == 7 || i == 12 || i == 17 || i == 22 ) {
        std::operator<<<...("-");
    }
​
    // 狀態更新公式 (核心數學邏輯)
    v11 *= 8LL;
    v11 += i + 64;
​
    // 延時處理
    v8 = 1;
    std::this_thread::sleep_for(...); // 每秒打印一個字符，增加儀式感
}

程序運行一個 for 循環，從 i = 0 到 31，總共生成 32 個字符

而我們也可以推導一下v11的狀態

• 初始值：v11_0 = 1

• 第一次迭代後：v11_1 = 1 * 8 + (0 + 64) = 72

• 第二次迭代後：v11_2 = 72 * 8 + (1 + 64) = 649

• 第三次迭代後：v11_3 = 649 * 8 + (2 + 64) = 5256

通過數學歸納法，可以得出v11的通項公式：

v11_k = 8^k * 1 + Σ(i=0到k-1) (i + 64) * 8^(k-1-i)

歸納化簡之後就是

v11_k = 8^k + Σ(j=0到k-1) (64 + j) * 8^(k-1-j)

其中j = k-1-i，這個公式展示了v11的指數級增長特性。隨着k的增大，v11的值會變得極其龐大：

• k = 8時：v11_8 ≈ 2.68 × 10^8

• k = 16時：v11_16 ≈ 7.2 × 10^16

• k = 32時：v11_32 ≈ 2.81 × 10^29

這種指數級增長意味着v11的範圍從1變化到約2^97

f函數

__int64 f(unsigned __int64 n) {   
    v5 = 0; v4 = 1;    
    for (i = 0; i < n; ++i) {        
        v2 = v4;        
        v4 = (v5 + v4) & 0xF;  // mod 16        
        v5 = v2;    }    
    return K[v5];
}

這明顯就是斐波那契數列取模運算

函數f的輸入是v11 mod 16的值，記為n，函數f計算斐波那契數列的第n項F(n)，然後對16取模，最後查表返回K[F(n) mod 16]

通過計算，前8個斐波那契數列值及其模16結果：

• F(0) = 0 → 0 mod 16 = 0

• F(1) = 1 → 1 mod 16 = 1

• F(2) = 1 → 1 mod 16 = 1

• F(3) = 2 → 2 mod 16 = 2

• F(4) = 3 → 3 mod 16 = 3

• F(5) = 5 → 5 mod 16 = 5

• F(6) = 8 → 8 mod 16 = 8

• F(7) = 13 → 13 mod 16 = 13

• F(8) = 21 → 21 mod 16 = 5

對於n=9及更大的值，斐波那契數列的模16結果呈現週期性，週期為24 這是因為斐波那契數列模m的週期，在m=16時為24

將v11 mod 16的週期規律與f函數的映射結合，得到最終的字符序列：

根據14週期規律，v11 mod 16的序列為[8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7, 8, 1, 2, 3, 4, 9, 6, 7]

將每個值輸入f函數：

• f(8) → K[5]

• f(1) → K[1]

• f(2) → K[1]

• f(3) → K[2]

• f(4) → K[3]

• f(9) → K[2]

• f(6) → K[8]

• f(7) → K[13]

以此類推，應用完整的14週期規律

全局字符表 K = "012ab9c3478d56ef"

def get_period():
    v5 = 0
    v4 = 1
    seq = [0]
    
    # Pisano period for 16 is 24.
    for _ in range(100): 
        v2 = v4
        v4 = (v5 + v4) & 0xF
        v5 = v2
        seq.append(v5)
        
    return 24, seq
​
def solve():
    period, sequence = get_period()
    
    K = "012ab9c3478d56ef"
    
    v11 = 1
    flag = ""
    
    print("flag{", end="")
    
    for i in range(32):
        # f(v11) returns K[sequence[v11 % period]]
        idx = sequence[v11 % period]
        c = K[idx]
        
        print(c, end="")
        flag += c
        
        if i in [7, 12, 17, 22]:
            print("-", end="")
            flag += "-"
            
        v11 = v11 * 8 + i + 64
        v11 &= 0xFFFFFFFFFFFFFFFF # Mask to 64 bits to simulate overflow
        
    print("}")
​
if __name__ == "__main__":
    solve()

2.3 RSA_NestingDoll

本題的get_smooth_prime 函數是漏洞存在的地方

在 get_smooth_prime(1024, 20, p1) 中，生成素數 p的邏輯本質上是

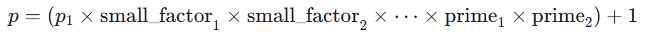
整理一下就會發現p−1=p1×K

其中 K是由一堆 20 位的小素數構成的

• 普通 RSA：p−1 是隨機的，包含大的隨機質因子，且這些因子完全不知道

• 本題 RSA：p−1雖然也包含一個巨大的質因子 p1，但這個 p1 恰好是已知量 n1 的一個因子

• 所以：n1就是打開 p−1的鑰匙，因為 n1=p1⋅q1⋅r1⋅s1，所以 n1 必然是 p1 的倍數。既然 p−1包含 p1，那麼 p−1

  的絕大部分因子都已經躺在 n1裏面了

import math
from Crypto.Util.number import *
from tqdm import tqdm
​
# --- 題目數據 ---
n1 = 16141229822582999941795528434053604024130834376743380417543848154510567941426284503974843508505293632858944676904777719167211264225017879544879766461905421764911145115313698529148118556481569662427943129906246669392285465962009760415398277861235401144473728421924300182818519451863668543279964773812681294700932779276119980976088388578080667457572761731749115242478798767995746571783659904107470270861418250270529189065684265364754871076595202944616294213418165898411332609375456093386942710433731450591144173543437880652898520275020008888364820928962186107055633582315448537508963579549702813766809204496344017389879
n = 484831124108275939341366810506193994531550055695853253298115538101629337644848848341479419438032232339003236906071864005366050185096955712484824249228197577223248353640366078747360090084446361275032026781246854700074896711976487694783856878403247312312487197243272330518861346981470353394149785086635163868023866817552387681890963052199983782800993485245670437818180617561464964987316161927118605512017355921555464359512280368738197370963036482455976503266489446554327046948670215814974461717020804892983665655107351050779151227099827044949961517305345415735355361979690945791766389892262659146088374064423340675969505766640604405056526597458482705651442368165084488267428304515239897907407899916127394598273176618290300112450670040922567688605072749116061905175316975711341960774150260004939250949738836358264952590189482518415728072191137713935386026127881564386427069721229262845412925923228235712893710368875996153516581760868562584742909664286792076869106489090142359608727406720798822550560161176676501888507397207863998129261472631954482761264406483807145805232317147769145985955267206369675711834485845321043623959730914679051434102698588945009836642922614296598336035078421463808774940679339890140690147375340294139027290793
c = 657984921229942454933933403447729006306657607710326864301226455143743298424203173231485254106370042482797921667656700155904329772383820736458855765136793243316671212869426397954684784861721375098512569633961083815312918123032774700110069081262242921985864796328969423527821139281310369981972743866271594590344539579191695406770264993187783060116166611986577690957583312376226071223036478908520539670631359415937784254986105845218988574365136837803183282535335170744088822352494742132919629693849729766426397683869482842748401000853783134170305075124230522253670782186531697976487673160305610021244587265868919495629
e = 65537
​
# 你之前找到的那個因子，我們可以直接用，減少工作量
known_factor = 12094541303222723616975666632268830751848445571951987169074250626437877110205699058506111384472586354084793914769711672322551034923778729430162356351731919
​
def get_primes(limit):
    ps = []
    is_p = [True] * (limit + 1)
    for p in range(2, limit + 1):
        if is_p[p]:
            ps.append(p)
            for i in range(p * p, limit + 1, p): is_p[i] = False
    return ps
​
print("[*] Generating primes...")
primes = get_primes(2**20 + 2000)
​
n1_factors = {known_factor}
curr_n = n
# 初始化 A。注意：要在當前的 curr_n 下運算
A = pow(3, n1, curr_n)
​
print("[*] Starting robust factorization...")
for p in tqdm(primes):
    # 計算 p 的最高冪次
    p_pow = p
    while p_pow * p <= 2**20:
        p_pow *= p
    
    A = pow(A, p_pow, curr_n)
    
    # 檢查當前因子
    g = math.gcd(A - 1, curr_n)
    
    # 如果找到了因子（哪怕是多個因子的乘積），我們都要處理
    if 1 < g < curr_n:
        # 這裏可能 g 包含了 p, q 等。為了提取 n1 的因子，
        # 我們需要嘗試把 g 裏的每一個素因子摳出來。
        # 簡單的方法：直接用 g 去試探 n1
        f = math.gcd(g - 1, n1)
        if f > 1:
            # 徹底分解 f
            temp_f = f
            for k in list(n1_factors):
                while temp_f % k == 0: temp_f //= k
            if temp_f > 1 and isPrime(temp_f):
                n1_factors.add(temp_f)
                print(f"\n[+] Found n1 factor: {temp_f}")
        
        # 核心改進：從當前模數中剔除已發現的因子，防止 GCD 變成 n
        curr_n //= g
        A %= curr_n
    
    elif g == curr_n:
        # 這種情況通常由於 base 的選擇導致，但在本邏輯中通過 A %= curr_n 極難發生
        # 如果發生了，説明當前的 A 已經在所有因子上都等於 1 了
        break
    
    if len(n1_factors) >= 4:
        break
​
# 補全邏輯
if len(n1_factors) == 3:
    p = 1
    for x in n1_factors: p *= x
    n1_factors.add(n1 // p)
​
if len(n1_factors) >= 4:
    factors = list(n1_factors)
    print("\n[!] All factors found. Decrypting...")
    phi = 1
    for f in factors: phi *= (f - 1)
    d = inverse(e, phi)
    m = pow(c, d, n1)
    flag = long_to_bytes(m)
    print("="*30)
    # 查找 flag 字符串
    if b'flag' in flag:
        print(flag[flag.find(b'flag'):].split(b'}')[0].decode() + '}')
    else:
        print(f"Decrypted (hex): {flag.hex()}")
    print("="*30)
else:
    print(f"\n[-] Still missing factors. Found: {len(n1_factors)}")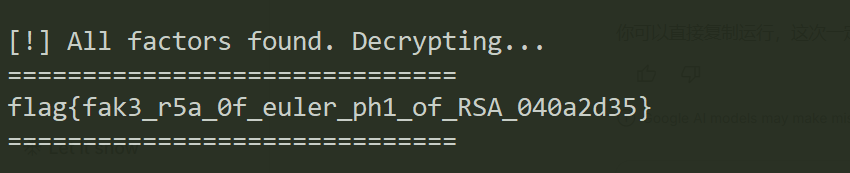

3.Re

3.1 wasm-login

需要一個工具 wasm2wat

截取一部分release.wat的代碼出來

(data (;42;) (i32.const 4296) "\02\00\00\00\1a\00\00\00{\00\22\00u\00s\00e\00r\00n\00a\00m\00e\00\22\00:\00\22")
(data (;44;) (i32.const 4344) "\02\00\00\00\1c\00\00\00\22\00,\00\22\00p\00a\00s\00s\00w\00o\00r\00d\00\22\00:\00\22")
(data (;53;) (i32.const 4584) "\02\00\00\00\1e\00\00\00\22\00,\00\22\00s\00i\00g\00n\00a\00t\00u\00r\00e\00\22\00:\00\22")
(data (;27;) (i32.const 2328) "\02\00\00\00\80\00\00\00N\00h\00R\004\00U\00J\00+\00z\005\00q\00F\00G\00i\00T\00C\00a\00A\00I\00D\00Y\00w\00Z\000\00d\00L\00l\006\00P\00E\00X\00K\00g\00o\00s\00t\00x\00u\00M\00v\008\00r\00H\00B\00p\003\00n\009\00e\00m\00j\00Q\00f\001\00c\00W\00b\002\00/\00V\00k\00S\007\00y\00O")

可以看到這裏有username password signature NhR4UJ+z5qFGiTCaAIDYwZ0dLl6PEXKgostxuMv8HBp3n9emjQf1cWb2/VkS7yO(這應該是張自定義的base64碼錶)

可以看出來這個程序在後台拼湊一個 JSON 字符串，包含用户名、密碼和某個簽名

username和password已經在題目給的index.html中找到

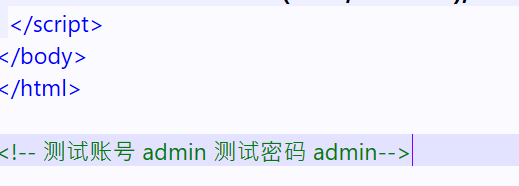
而index.html中還發現md5的開頭部分

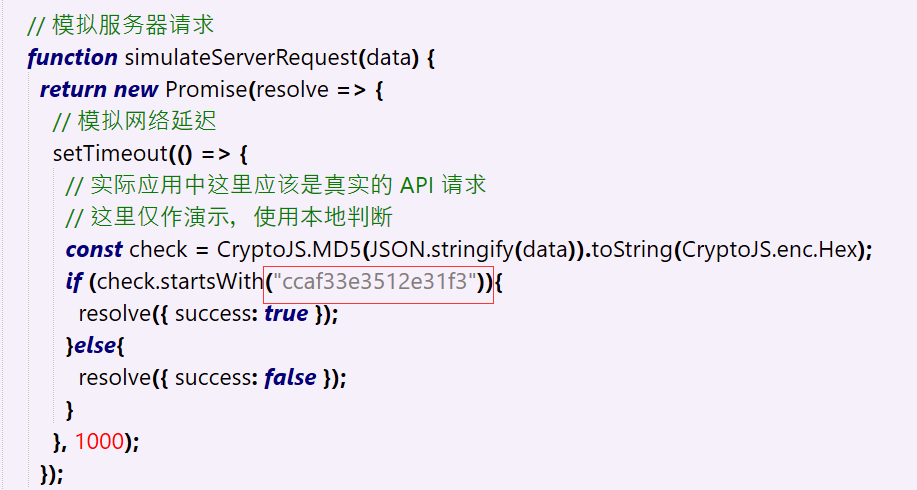
const check = CryptoJS.MD5(JSON.stringify(data)).toString(CryptoJS.enc.Hex);

• JSON.stringify(data): 這一步是把傳進來的數據，比如包含用户名、密碼、簽名的對象變成一個字符串

• CryptoJS.MD5(...): 對這個字符串進行 MD5 哈希計算

• .toString(CryptoJS.enc.Hex): 把計算結果轉換成 十六進制字符串

• 結論：變量 check 的值就是一個 MD5 哈希字符串

if (check.startsWith("ccaf33e3512e31f3")){
    resolve({ success: true });
}

• startsWith("..."): 這是 JavaScript 的字符串方法，意思是判斷字符串是否以指定的子字符串開頭

• resolve({ success: true }): 只有當條件成立，返回 true時，服務器才會告訴前端驗證通過或登錄成功

通過上面的代碼，可以得出以下邏輯鏈條：

1. 目標：讓函數返回 success: true

2. 條件：check 變量必須以 "ccaf33e3512e31f3" 開頭

3. check 的本質：它是輸入數據的 MD5 值

4. 結論：需要找到一個輸入數據，包含正確的時間戳，使得它的 MD5 值的前 16 位 正好是 ccaf33e3512e31f3

接着看程序的常量

 if  ;; label = @1
      i32.const 1779033703
      global.set 1
      i32.const -1150833019
      global.set 2
      ...

• 把這些數字轉成十六進制：

  • 1779033703 -> 0x6a09e667

  • -1150833019 -> 0xbb67ae85

• 去搜索引擎搜這些十六進制數，就會知道這是 SHA-256 的標準初始常量

程序使用了 SHA-256 加密。結合 func 33 裏的 xor 118 和 xor 60，這正是 HMAC-SHA256

因為xor 常量 118 (0x76) 和 60 (0x3c)，這是 HMAC 算法中 ipad 和 opad 的典型特徵

而根據題目內容

題目內容：
某人本想在2025年12月第三個週末爆肝一個web安全登錄demo，結果不僅搞到週一凌晨，他自己還忘了成功登錄時的時間戳了，你能幫他找回來嗎？
​
提交格式為flag{時間戳正確時的check值}。是一個大括號內為一個32位長的小寫十六進制字符串

題目説：2025年12月第三個週末，一直搞到週一凌晨。

2025年12月21日（週日），22日（週一）

• 2025-12-22 00:00:00 -> 1766332800000

• 2025-12-22 02:00:00 -> 1766340000000

所以範圍大概就在這中間

import hashlib
from datetime import datetime, timezone, timedelta
​
class CryptoEngine:
    """內部安全引擎 - 負責令牌生成與校驗"""
    def __init__(self):
        # 混淆過的映射表
        self._alphabet = "NhR4UJ+z5qFGiTCaAIDYwZ0dLl6PEXKgostxuMv8rHBp3n9emjQf1cWb2/VkS7yO"
        self._user_info = ("admin", "admin")
        self._goal_prefix = "ccaf33e3512e31f3"
​
    def _transform(self, data: bytes) -> str:
        """核心編碼邏輯：自定義位流映射"""
        out = []
        val, bits = 0, 0
        for byte in data:
            val = (val << 8) | byte
            bits += 8
            while bits >= 6:
                bits -= 6
                out.append(self._alphabet[(val >> bits) & 0x3F])
        
        if bits > 0:
            out.append(self._alphabet[(val << (6 - bits)) & 0x3F])
            
        res = "".join(out)
        # 補齊長度
        return res + ("=" * ((4 - len(res) % 4) % 4))
​
    def check_sequence(self, tick: int) -> str:
        """計算特定時間戳下的認證指紋"""
        u, p = self._user_info
        # 預處理密碼編碼
        p_enc = self._transform(p.encode('latin-1'))
        
        # 構造原始載荷
        payload = '{"username":"%s","password":"%s"}' % (u, p_enc)
        raw_msg = payload.encode('utf-8')
​
        # 密鑰派生 (Key Derivation)
        seed = str(tick).encode()
        key_block = hashlib.sha256(seed).digest() if len(seed) > 64 else seed
        key_block = key_block.ljust(64, b'\x00')
​
        # 這裏的 118(0x76) 和 60(0x3C) 是原始邏輯的特徵常數
        p1 = bytes([b ^ 118 for b in key_block])
        p2 = bytes([b ^ 60 for b in key_block])
​
        # 嵌套哈希架構 (注意：這是非標準的哈希順序 inner + opad)
        mid_hash = hashlib.sha256(p1 + raw_msg).digest()
        final_sig = self._transform(hashlib.sha256(mid_hash + p2).digest())
​
        # 生成最終校驗體
        full_body = '{"username":"%s","password":"%s","signature":"%s"}' % (u, p_enc, final_sig)
        return hashlib.md5(full_body.encode()).hexdigest()
​
    def run_audit(self):
        """執行掃描任務"""
        # 時間範圍定義
        tz = timezone(timedelta(hours=8))
        t_start = int(datetime(2025, 12, 22, 0, 0, tzinfo=tz).timestamp() * 1000)
        t_end = int(datetime(2025, 12, 22, 6, 0, tzinfo=tz).timestamp() * 1000)
​
        print(f"[*] Task started: scanning range {t_start} -> {t_end}")
        
        total = t_end - t_start
        for current_ts in range(t_start, t_end + 1):
            token = self.check_sequence(current_ts)
            
            if token.startswith(self._goal_prefix):
                print(f"\n[+] Match discovered at index: {current_ts}")
                print(f"[+] Final Flag: flag{{{token}}}")
                return
​
            if current_ts % 100000 == 0:
                progress = (current_ts - t_start) / total * 100
                print(f"[*] Processing... {progress:.1f}%", end='\r')
​
if __name__ == "__main__":
    engine = CryptoEngine()
    engine.run_audit()

3.2 babygame

一道Godot逆向題，得有專門的工具

extends CenterContainer
​
@onready var flagTextEdit: Node = $PanelContainer / VBoxContainer / FlagTextEdit
@onready var label2: Node = $PanelContainer / VBoxContainer / Label2
​
static var key = "FanAglFanAglOoO!"
var data = ""
​
func _on_ready() -> void :
    Flag.hide()
​
func get_key() -> String:
    return key
​
func submit() -> void :
    data = flagTextEdit.text
​
    var aes = AESContext.new()
    aes.start(AESContext.MODE_ECB_ENCRYPT, key.to_utf8_buffer())
    var encrypted = aes.update(data.to_utf8_buffer())
    aes.finish()
​
    if encrypted.hex_encode() == "d458af702a680ae4d089ce32fc39945d":
        label2.show()
    else:
        label2.hide()
​
func back() -> void :
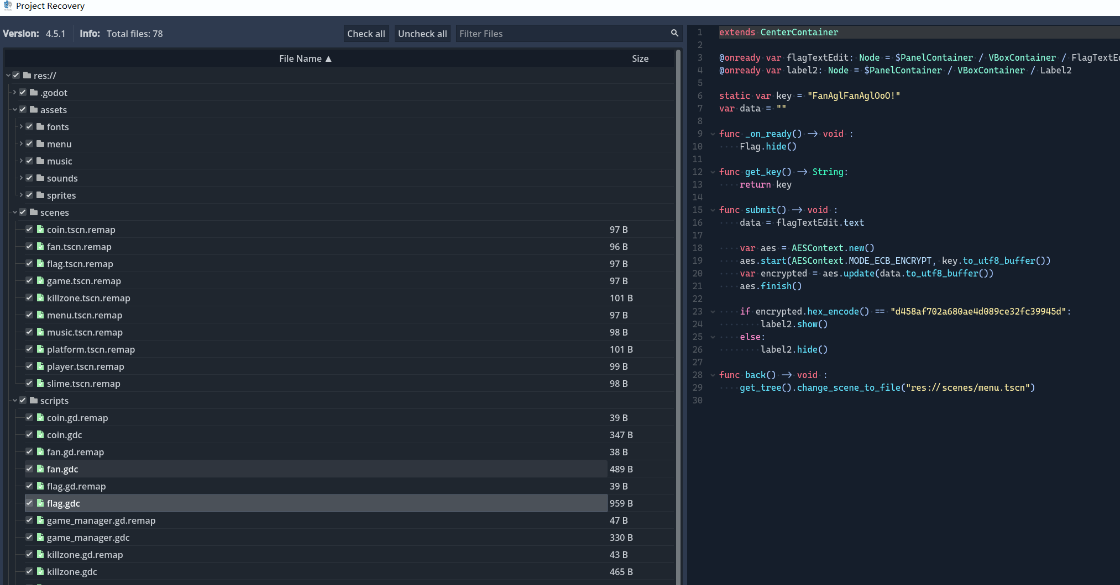
    get_tree().change_scene_to_file("res://scenes/menu.tscn")

可以看到

• 初始key：FanAglFanAglOoO!

• 目標密文hex：d458af702a680ae4d089ce32fc39945d

• 算法 是 AES ，代碼中明確調用了 AESContext.new()

• 模式是 ECB 代碼中使用了 AESContext.MODE_ECB_ENCRYPT

• 密鑰 FanAglFanAglOoO!

  • 該字符串長度為 16 個字符。

  • 在 UTF-8 編碼下，16 個字符等於 16 字節（128位），因此，這是 AES-128

照理説直接寫個腳本逆向就可以得到flag了，可是一直不對

然後看了題目內容

題目內容：
請找出隱藏的Flag。請注意只有收集了所有的金幣，才能驗證flag。

意思就是金幣，也就是分數得達到一個設定好的數才能驗證flag，回去逆向看看那裏關於分數的函數

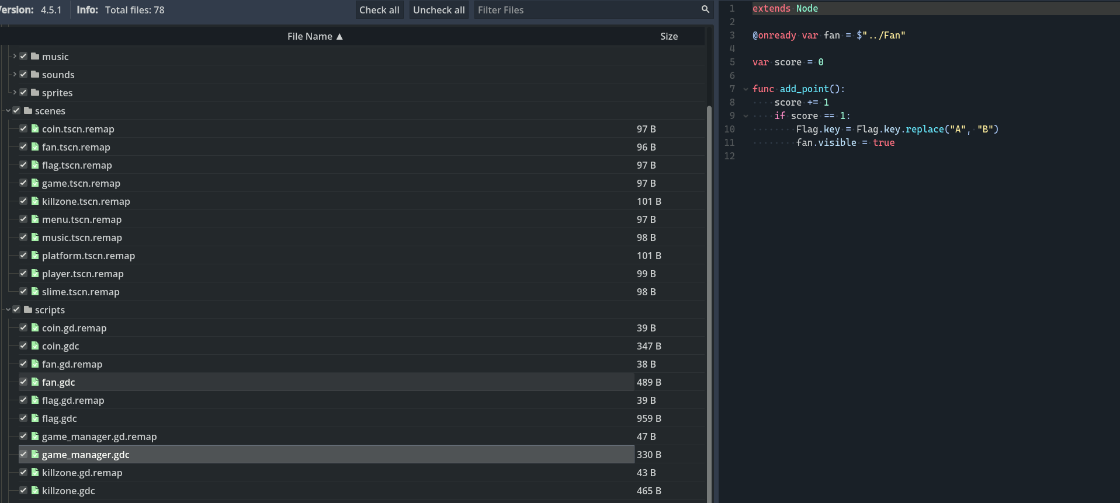
可以看到分數這裏的代碼是説當分數+1的時候，密鑰中的A替換成B

所以正確的密鑰應該是

FanBglFanBglOoO!

所以套上腳本就是

from Crypto.Cipher import AES
key = b"FanBglFanBglOoO!"
ciphertext = bytes.fromhex("d458af702a680ae4d089ce32fc39945d")
cipher = AES.new(key, AES.MODE_ECB)
result = cipher.decrypt(ciphertext)
print(result)

更多網安技能的在線實操練習，請點擊這裏>>