博客 / 詳情

返回

淺析如何在逆向中分析AES算法

AES算法淺析

AES是對稱加密算法，在逆向中常常使用到，白盒AES算法詳解這篇文章寫的非常好，通俗易懂。但是我在原理到代碼的過程經常會卡殼，因此結合C語言代碼淺析一下算法。

這裏使用的源碼為https://github.com/kokke/tiny-AES-c

密鑰擴展

這裏以AES-128為例子（以下用AES代替），初始時輸入的密鑰長度是16字節的，因此每次加密的長度的明文也需要與之匹配，在加密之前，需要將明文分割成16字節長度為一組，然後分割為若干組進行加密，與下圖一致（ECB加密模式）。

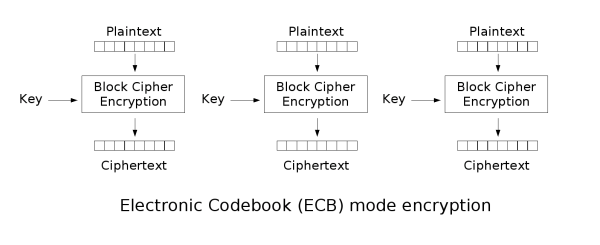
undefined

由於AES加密需要經過10輪加密，因此需要11個密鑰（每輪一個+初始一個），因此需要利用輸入的初始密鑰生成剩下的10個密鑰，這個生成密鑰的過程就稱之為密鑰擴展，如下圖所示，k0-k3為初始密鑰，每一塊為4個字節。其餘k4-k44就是通過初始密鑰k0-k3經過密鑰擴展計算得到

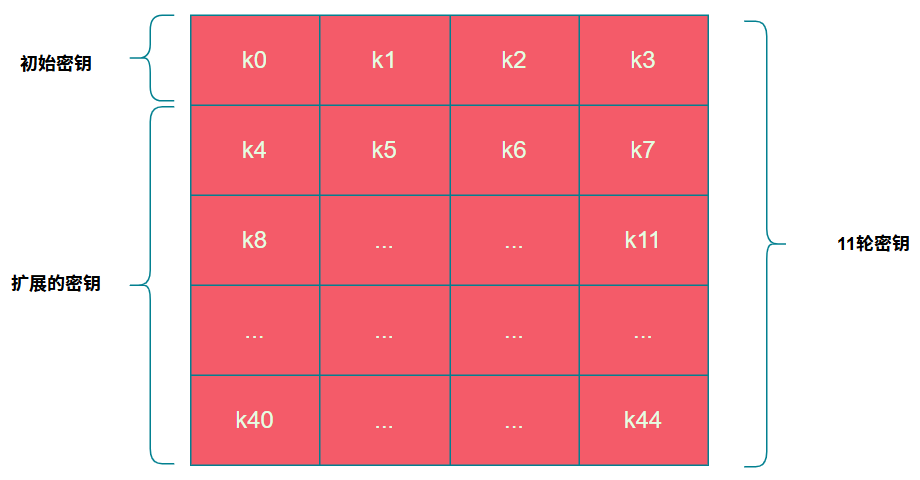
image-20251114220140556

擴展密鑰依賴公式$k_n=k{n-1}\oplus k{n-4}$ 即密鑰$k_5=k_4\oplus k_1$，依次類推。

但是k4、k8...k40擴展密鑰比較特殊，需要經過G運算後再進行異或，即$k4=G(k_3)\oplus k_0$

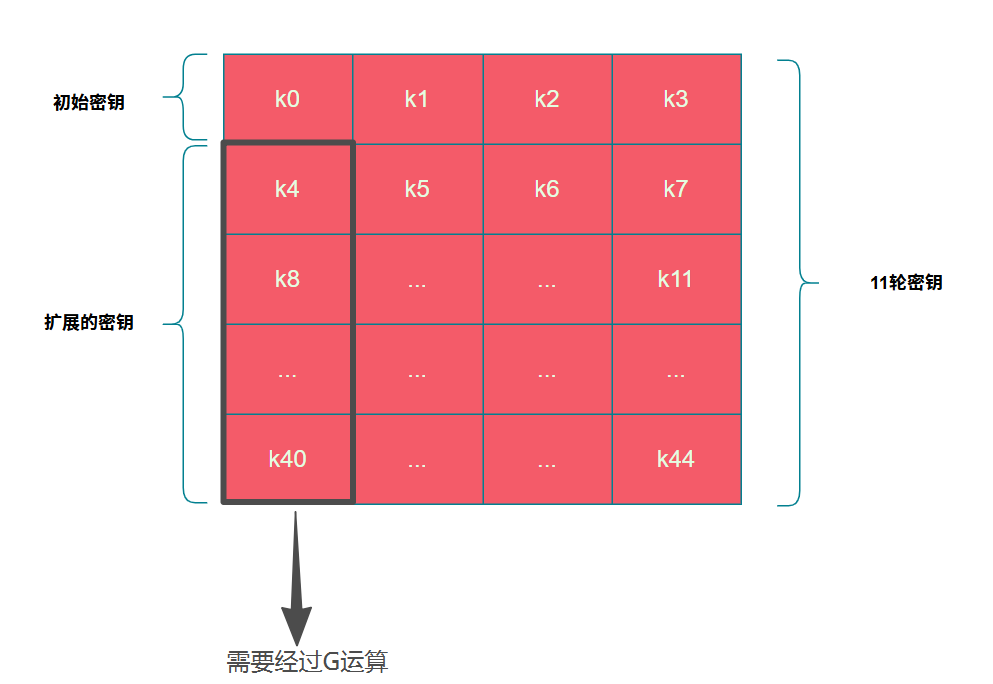
image-20251114221805876

G運算

G運算就是將密鑰進行行位移、S盒替換、以及跟一個常數進行異或得到最後的結果，這裏我們假設k3=0x11223344

image-20251114222301745

行位移

行位移實際是做了一個循環左移的操作，將每個字節往左移動了一個字節

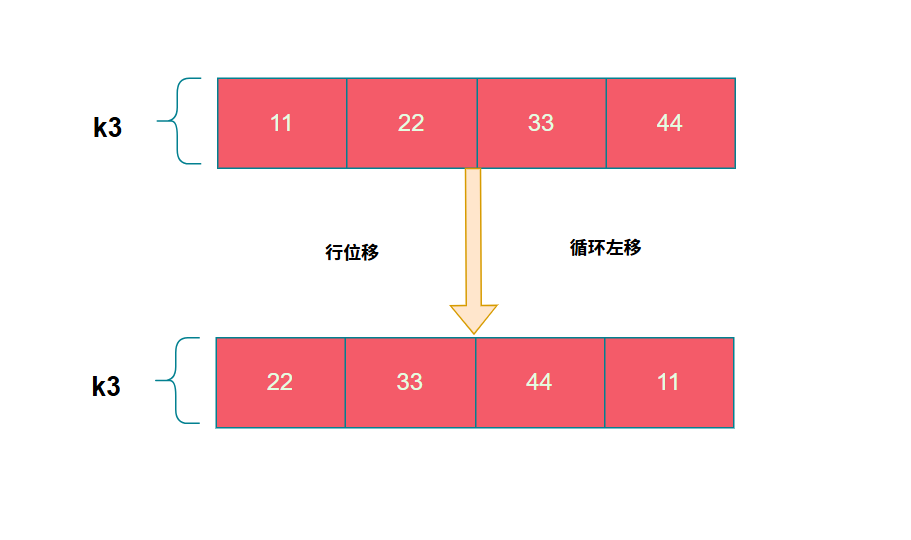
image-20251114222508769

在tiny-AES-c中行位移的實現使用字符轉換實現。

...
    {
        //行位移
        const uint8_t u8tmp = tempa[0];
        tempa[0] = tempa[1];
        tempa[1] = tempa[2];
        tempa[2] = tempa[3];
        tempa[3] = u8tmp;
     }
...

S盒替換

S盒則是一個長度為256的數組，其中會放置一些具體的數值。S盒的替換則是將字節的值作為下標去數值找到對應的值。

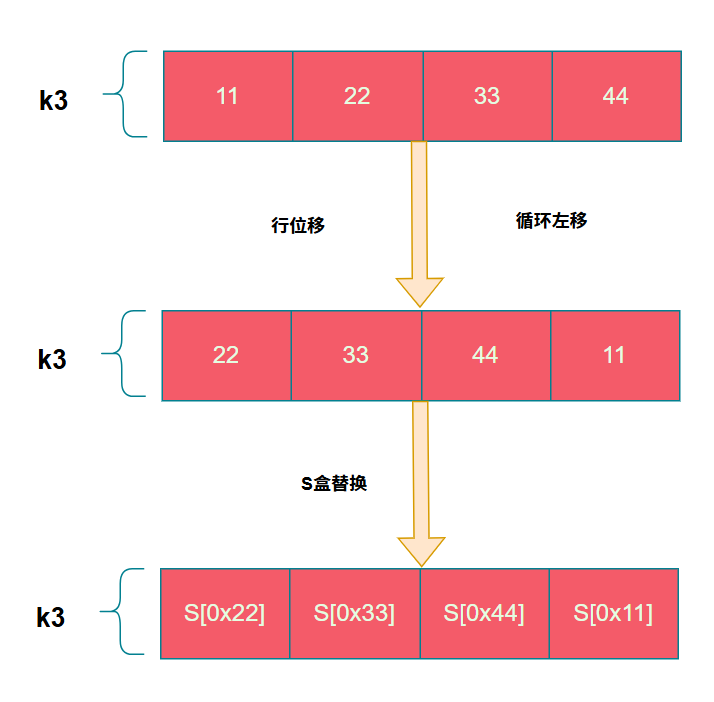
image-20251114222911172

其中S盒的數值如下，因此可以依據S盒的值作為AES算法的特徵值

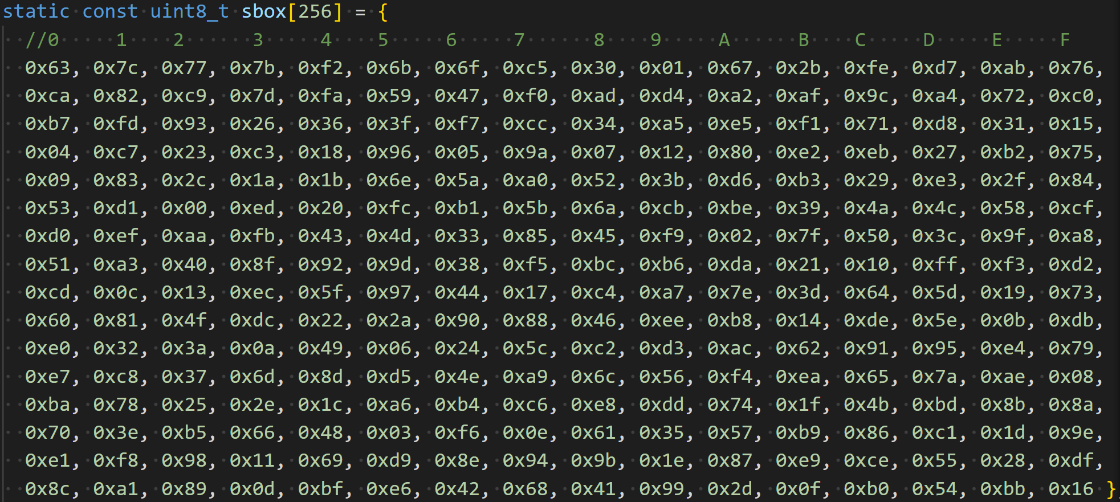
image-20251114222950328

而S盒的替換則是首先定義sbox數組，如上圖。然後將行位移後的密鑰字節值作為下標直接在sbox中取值，如下述代碼。

#define getSBoxValue(num) (sbox[(num)])
     ...
     {
        tempa[0] = getSBoxValue(tempa[0]);
        tempa[1] = getSBoxValue(tempa[1]);
        tempa[2] = getSBoxValue(tempa[2]);
        tempa[3] = getSBoxValue(tempa[3]);
      }
     ...

常量異或

其中常量是存儲在名為Rcon的數組中

image-20251114223521935

緊接着將S盒替換後的結果與這些常量進行異或，其中n代表的是輪數，剛好對應Rcon數組的10個值，用於後續10輪擴展，這裏需要注意的是Rcon數組是以下標1為起始位置，並且Rcon數組每一個元素的大小隻佔用一個字節，因此需要使用密鑰的第一個字節異或即可。

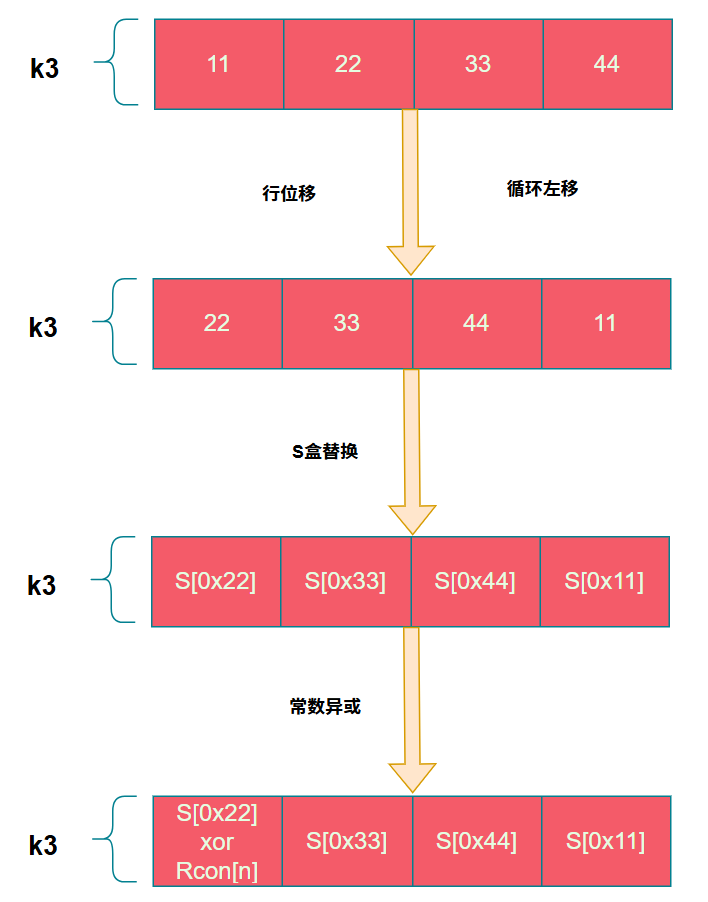
image-20251115080441547

最後一步就是常量異或，這裏跟上述説的一樣只需要取第一個字節異或即可，這裏NK=4，那麼i的值只會取$4、8、12....40$，因此$\frac{i}{NK}$剛好代表的是輪數，第一輪則使用Rcon[1]異或，第二輪則用Rcon[2]以此類推。

      //常量異或
      tempa[0] = tempa[0] ^ Rcon[i/Nk];

最終得到的值就是經過G運算後的值了，那麼我們的擴展後的密鑰k4則是經過G運算後的k3與k0進行異或，即$k4=G(k_3)\oplus k_0$，這裏需要注意的是，代碼是以字節為單位處理的，而在AES算法中$k_n$是以4字節為單位處理，所以這裏處理下標的時候使用了$i*4$。無論密鑰是否經過G運算，都可以使用下述代碼進行異或處理，若是經過G函數那麼tempa則存儲$G(k{n-1})$，反之則存儲$k{n-1}$

    ...
    //j為密鑰具體字節的下標，k代表的是n-4,tempa數組存儲經過G函數處理後的密鑰字節
    j = i * 4; k=(i - Nk) * 4;
    RoundKey[j + 0] = RoundKey[k + 0] ^ tempa[0];
    RoundKey[j + 1] = RoundKey[k + 1] ^ tempa[1];
    RoundKey[j + 2] = RoundKey[k + 2] ^ tempa[2];
    RoundKey[j + 3] = RoundKey[k + 3] ^ tempa[3];
    ...

加密階段

在加密之前，需要將明文轉換為state，具體轉換過程如下圖，其實很簡單，就是列存儲明文數據。

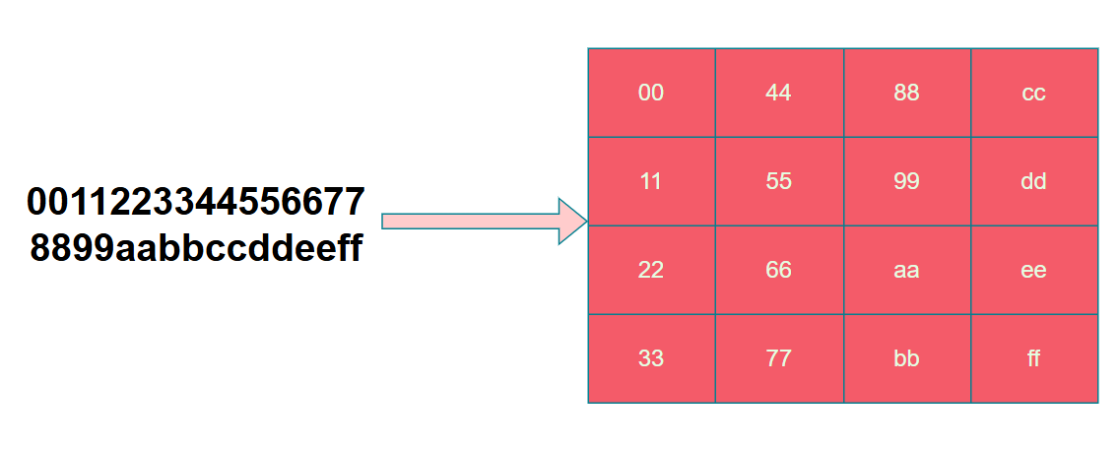
image-20251115082240455

具體加密過程如下圖，需要先經過輪密鑰加、字節替換、行位移、列混淆，其中最後一輪不需要列混淆的操作。。

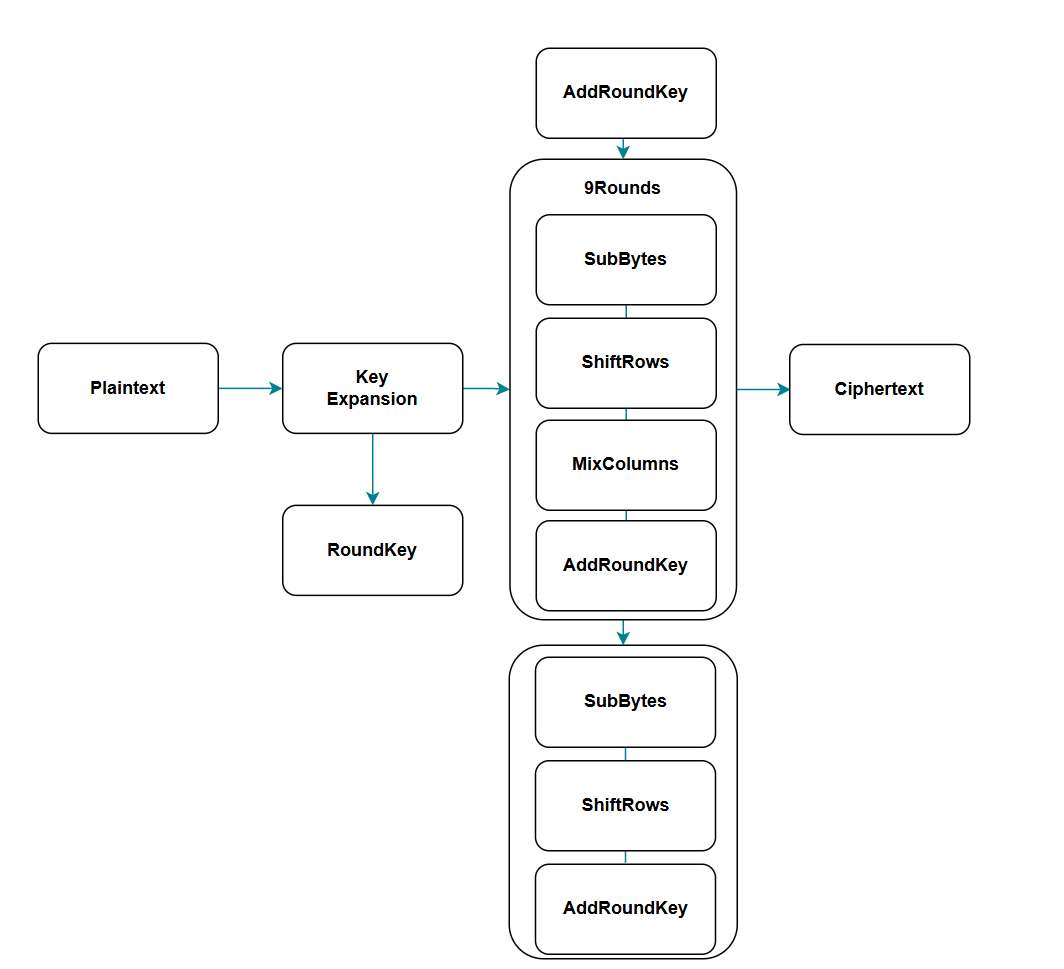
image-20251115111738651

輪密鑰加

在AES算法中，加法都是異或操作，因此輪密鑰加就是按字節將明文與密鑰進行異或操作，如下圖所示。

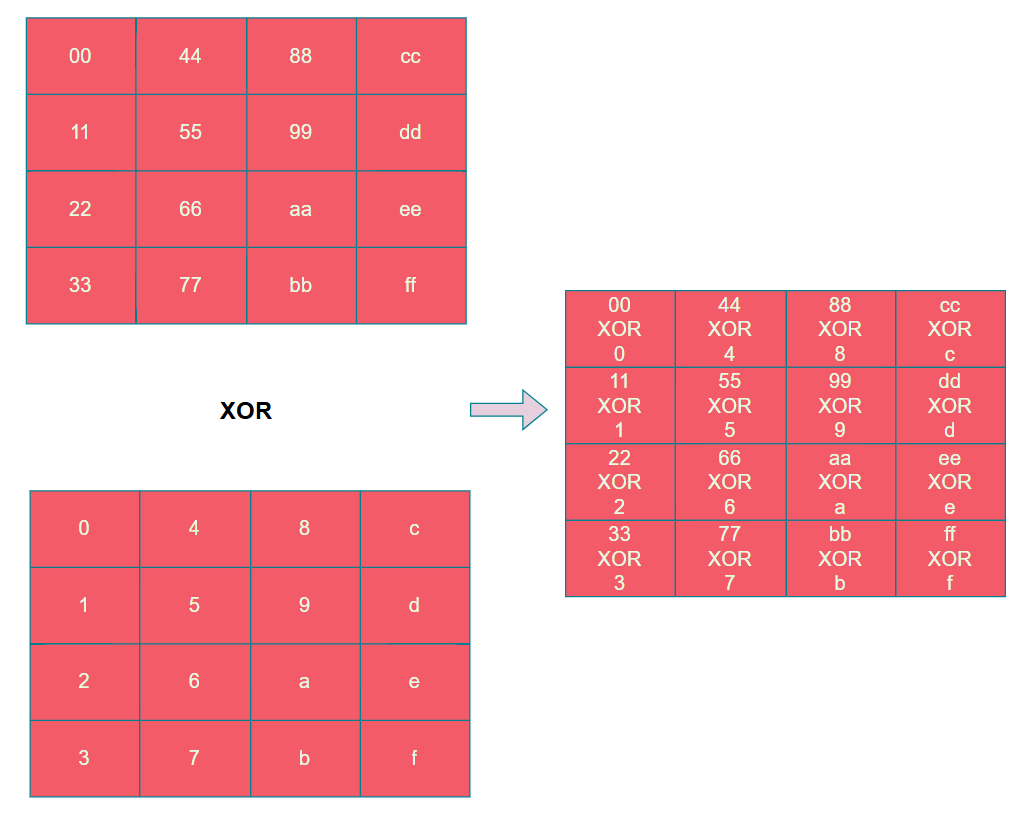
image-20251115121555484

在tiny-AES-c，state實際上是按照行進行存儲的，但是輪密鑰加的環節進行的字節異或，因此按照行存儲的方式逐字節取出明文與密鑰進行異或不會影響結果，如下列代碼所示。

static void AddRoundKey(uint8_t round, state_t* state, const uint8_t* RoundKey)
{
  uint8_t i,j;
  //輪密鑰加，逐個字節異或
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      //每輪密鑰是16字節
      (*state)[i][j] ^= RoundKey[(round * Nb * 4) + (i * Nb) + j];
    }
  }
}

字節替換

字節替換與密鑰擴展中的S盒替換一致。這裏就是行列取出字節，然後進行S盒的替換。

static void SubBytes(state_t* state)
{
  uint8_t i, j;
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      (*state)[j][i] = getSBoxValue((*state)[j][i]);
    }
  }
}

行位移

行位移則是以state為單位，進行逐行的循環左移，如下圖所示，第一行不移動，第二行移動1個字節，第三行移動2個字節，第四行移動3個字節。

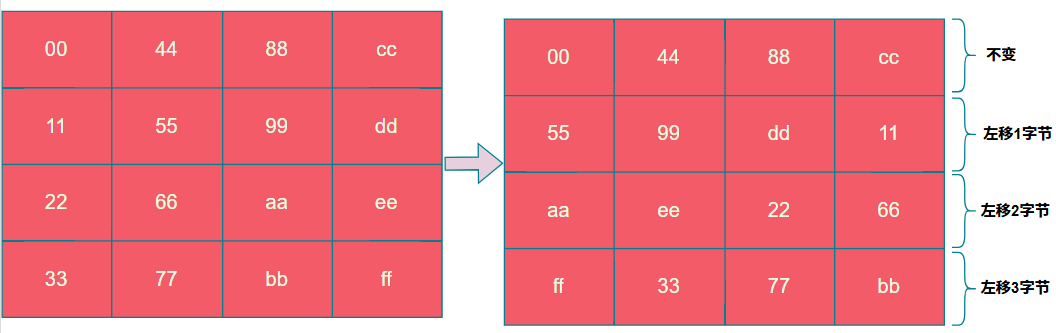
image-20251115122746408

由於在tiny-AES-c中是將明文以行存儲的方式轉換state的，因此移位的時候需要以列的方式進行移位。

static void ShiftRows(state_t* state)
{
  uint8_t temp;
​
  // Rotate first row 1 columns to left  
  //[1][1]移動到[0][1]向上移動1個字節
  temp           = (*state)[0][1];
  (*state)[0][1] = (*state)[1][1];
  (*state)[1][1] = (*state)[2][1];
  (*state)[2][1] = (*state)[3][1];
  (*state)[3][1] = temp;
​
  // Rotate second row 2 columns to left 
  //[2][2]移動到[2][2]向上移動2個字節  
  temp           = (*state)[0][2];
  (*state)[0][2] = (*state)[2][2];
  (*state)[2][2] = temp;
​
  temp           = (*state)[1][2];
  (*state)[1][2] = (*state)[3][2];
  (*state)[3][2] = temp;
​
  // Rotate third row 3 columns to left
  //[3][3]移動到[0][3]向上移動3個字節
  temp           = (*state)[0][3];
  (*state)[0][3] = (*state)[3][3];
  (*state)[3][3] = (*state)[2][3];
  (*state)[2][3] = (*state)[1][3];
  (*state)[1][3] = temp;
}

上述代碼的意思如下圖所示，我們只需要把表格翻轉一下，那麼向左移動就相當於向上移動了。

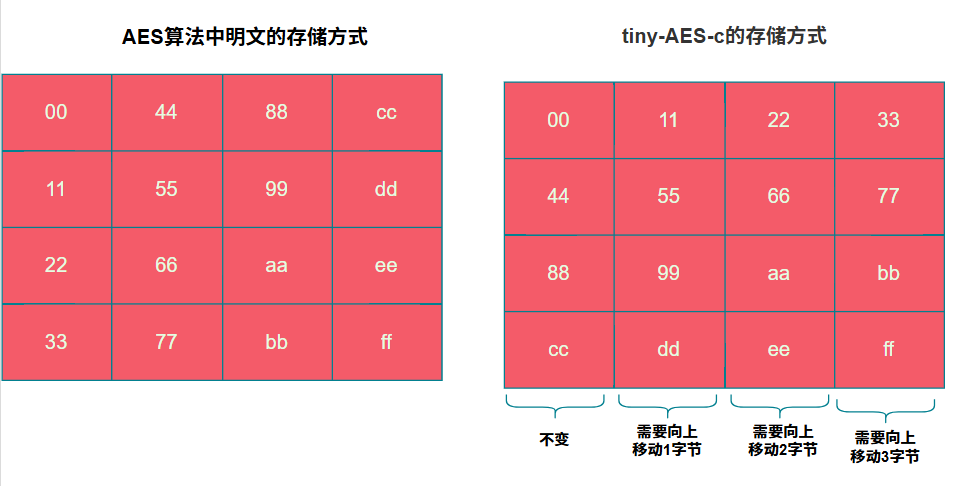
image-20251115123733254

列混淆

列混淆則是通過矩陣的乘法實現的

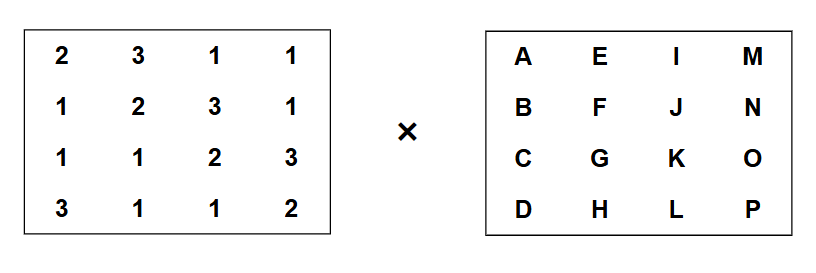
image-20251115212132121

最終得到的式子如下所示

  1. $2A+3B+C+D$

  2. $A+2B+3C+D$

  3. $A+B+2C+3D$

  4. $3A+B+C+2D$

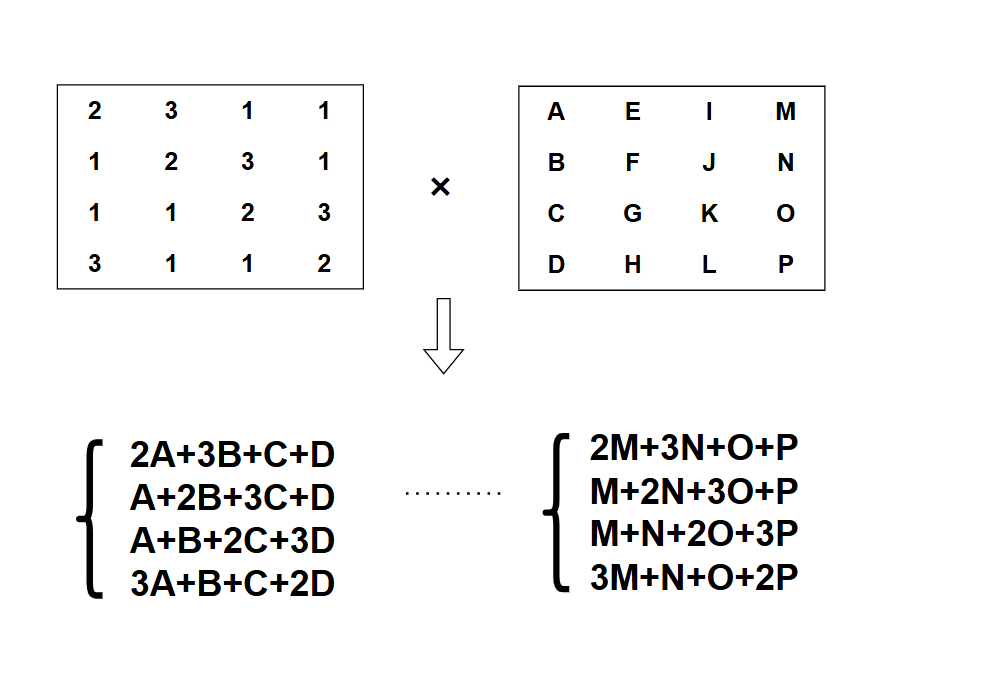
image-20251115212809826

在AES算法中加法就是異或，因此式子就變為

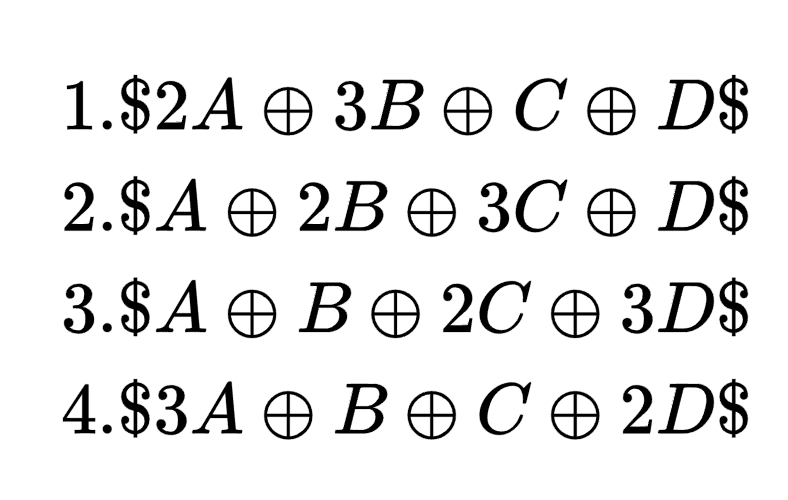
image-20251118104534589

其中乘法是伽羅瓦域內乘法($GF(2^8)$)，根據上述的式子由三種情況，$1A$、$2A$、以及$3*A$

  • $1*A = A$

  • $2*A$，則是將$A << 1$，但是需要判斷左移後是否有溢出發生，若發生溢出還需要加上0x1b

  • $3A = 2A + A$

在tiny-AES-c中實現的列混淆如下所示，首先xtime為二倍乘的實現，首先判斷是否有溢出發生，若有則異或0x1b，反之則不用。

【----幫助網安學習，以下所有學習資料免費領！加vx：YJ-2021-1，備註 “博客園” 獲取！】

　① 網安學習成長路徑思維導圖
　② 60+網安經典常用工具包
　③ 100+SRC漏洞分析報告
　④ 150+網安攻防實戰技術電子書
　⑤ 最權威CISSP 認證考試指南+題庫
　⑥ 超1800頁CTF實戰技巧手冊
　⑦ 最新網安大廠面試題合集（含答案）
　⑧ APP客户端安全檢測指南（安卓+IOS）

在具體的列混淆中有一個便捷操作就是先計算出

image-20251118104558320

這是因為每一次的列混淆都需要計算該值，因此提前計算避免重複操作，這裏以

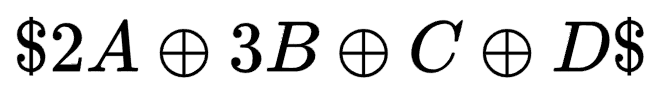
image-20251118104616288

為例。

image-20251118104642152

因此列混淆的計算可以化簡三個部分

  • 二倍乘的計算

  • 公共部分的計算

  • 自身值

//xtime為GF(2^8)的二倍乘
static uint8_t xtime(uint8_t x)
{
  //左移一位相當於乘以2，然後右移7位判斷最高位是否位1，為1就需要異或0x1b，否則不用
  //最高位為1，左移會溢出，因此需要加上0x1b，再GF(2^8)中加法等於異或
  return ((x<<1) ^ (((x>>7) & 1) * 0x1b));
}
​
// MixColumns function mixes the columns of the state matrix
static void MixColumns(state_t* state)
{
  uint8_t i;
  uint8_t Tmp, Tm, t;
  for (i = 0; i < 4; ++i)
  {  
    //t是A
    t   = (*state)[i][0];
    //先求a[0]^a[1]^a[2]^a[3]，因為這是求解的公共部分，避免重複操作
    Tmp = (*state)[i][0] ^ (*state)[i][1] ^ (*state)[i][2] ^ (*state)[i][3] ;
    //2A+3B+C+D = 2A+2B+B+C+D = 2*(A+B)+B+C+D = 2*(A+B)+(A+B+C+D)+A 
    Tm  = (*state)[i][0] ^ (*state)[i][1] ; Tm = xtime(Tm);  (*state)[i][0] ^= Tm ^ Tmp ;
    //A+2B+3C+D
    Tm  = (*state)[i][1] ^ (*state)[i][2] ; Tm = xtime(Tm);  (*state)[i][1] ^= Tm ^ Tmp ;
    //A+B+2C+3D
    Tm  = (*state)[i][2] ^ (*state)[i][3] ; Tm = xtime(Tm);  (*state)[i][2] ^= Tm ^ Tmp ;
    //3A+B+C+2D
    Tm  = (*state)[i][3] ^ t ;              Tm = xtime(Tm);  (*state)[i][3] ^= Tm ^ Tmp ;
  }
}

逆向中AES的識別

這裏以[SCTF2019]creakme為例，從ida的反編譯中識別AES算法

密鑰擴展

首先在看到一串明文字符時，可以根據該字符串長度去判斷是否為密鑰以及AES算法的種類，下圖中存在着字符串sycloversyclover，該字符串的長度為16，以及有字符串拆分成字節的形式進行存儲，根據tiny-AES-c源碼分析可知，在實際操作中，需要將密鑰以字節的形式進行操作，因此根據長度以及字節存儲的操作，可以猜測此算法可能為AES-128，該字符串為密鑰。

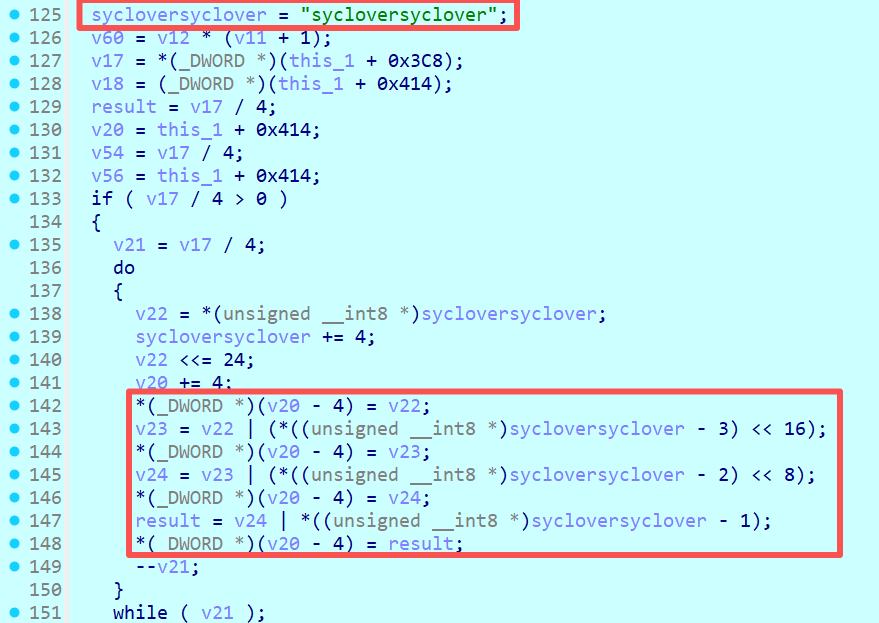
image-20251115215546915

在結合下述操作可以發現，在代碼185行中具有S盒替換（S_BOX[v31]）、行位移（<<8），可以看到在ida的反編譯中會將G運算集成在一步中。

image-20251115220210972

那麼G運算中還存在一個常量異或的操作，因此*v32大概率是取出Rcon數組值的操作，而v32由v59賦值而來，v59又由unk_406B40賦值而來，那麼查看unk_406B40的值，確實是Rcon數組值一致，驗證了該算法就是AES算法，並且該函數是密鑰擴展的操作。

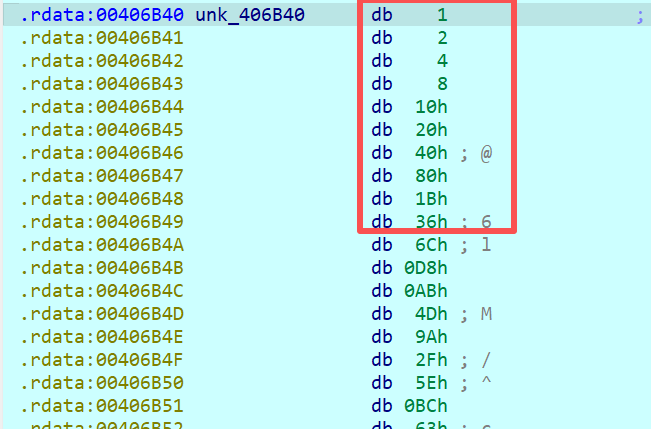
image-20251115220618246

那麼還有一個關鍵點可以分析，那就是循環的次數，由於密鑰擴展需要擴展到$k_{44}$，因此循環的下標最大值也為44，循環次數也能對上。

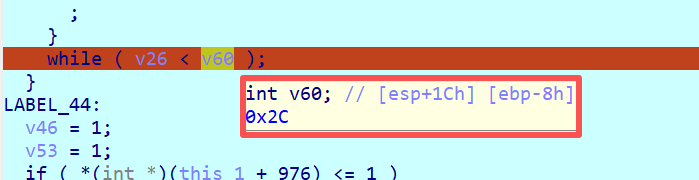
image-20251115220724617

加密階段

在加密階段實際上可以直接看最後一輪，因為最後一輪的加密操作中是不需要進行列混淆的，如下圖所示進行很明顯進行了S盒替換與輪密鑰加，這裏可能大家疑惑，那行位移去哪裏了？仔細看，實際上每次進行S盒替換的變量是不一樣的，分別是v21、v5、v23以及v24我在圖中給大家標記出來，而上述這些變量都是int類型的，實際上就是每次都存儲4字節，那麼就相當於按行存儲了，在AES算法淺析部分跟大家分析過，若是按行存儲的，那麼就列往上移動即可，所以第二次的順序就變成了v5、v23、v24、v21了。

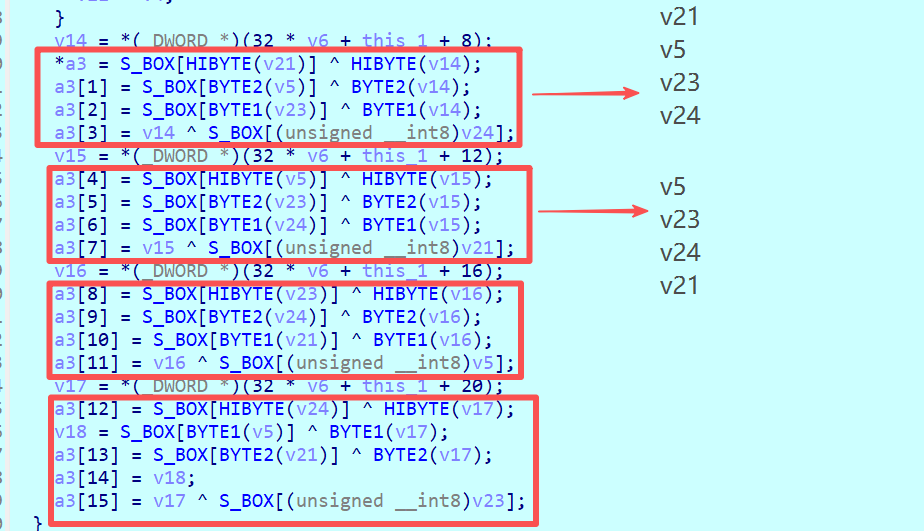
image-20251115221637087

那麼説明上面的部分實際上就增加列混淆的操作，但是這部分操作確實是有字節替換，但是好像替換的數據並不是S盒？

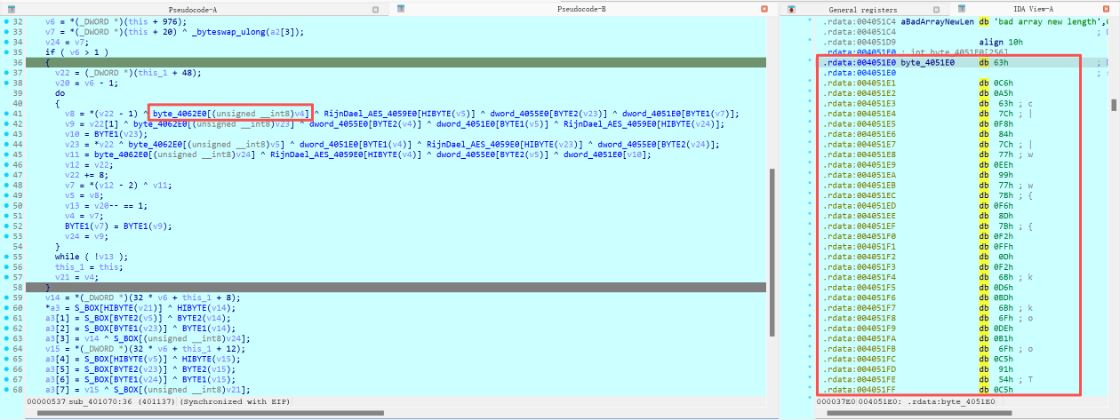
image-20251115222147517

實際上這是AES算法以空間換時間的實現，即T盒（T-table)實現。在上述提到的實現中，是首先將明文輸入->輪密鑰加->s盒替換->行位移->列混淆，這些操作實際上都是以字節為單位進行運算的，字節之間是不會相互影響的，那麼一個字節的範圍為0-255，將該範圍的所有情況進行s盒替換->行位移->列混淆的結果先計算好，並將該結果集稱之為T盒（T-table），那麼當輸入一個明文字節時，只需要做一個T盒的替換就可以立刻得到上述過程的結果，極大節約了運算的時間。因此這也是為啥替換的表不是S盒的原因。

那麼而根據上述分析可以得出該函數為加密階段函數。

加密模式

實際上在分析出密鑰擴展或加密階段的操作之後都可以比較明確的分析出該程序使用的算法了，但是為什麼還是最好能夠快速區分出這兩個階段呢？因為對稱加密還存在加密模式，如ECB、CBC、CFB等，可以看到在加密階段之前會與v15進行異或，那麼可以猜測為CBC的加密模式，那麼就需要找IV初始向量值。

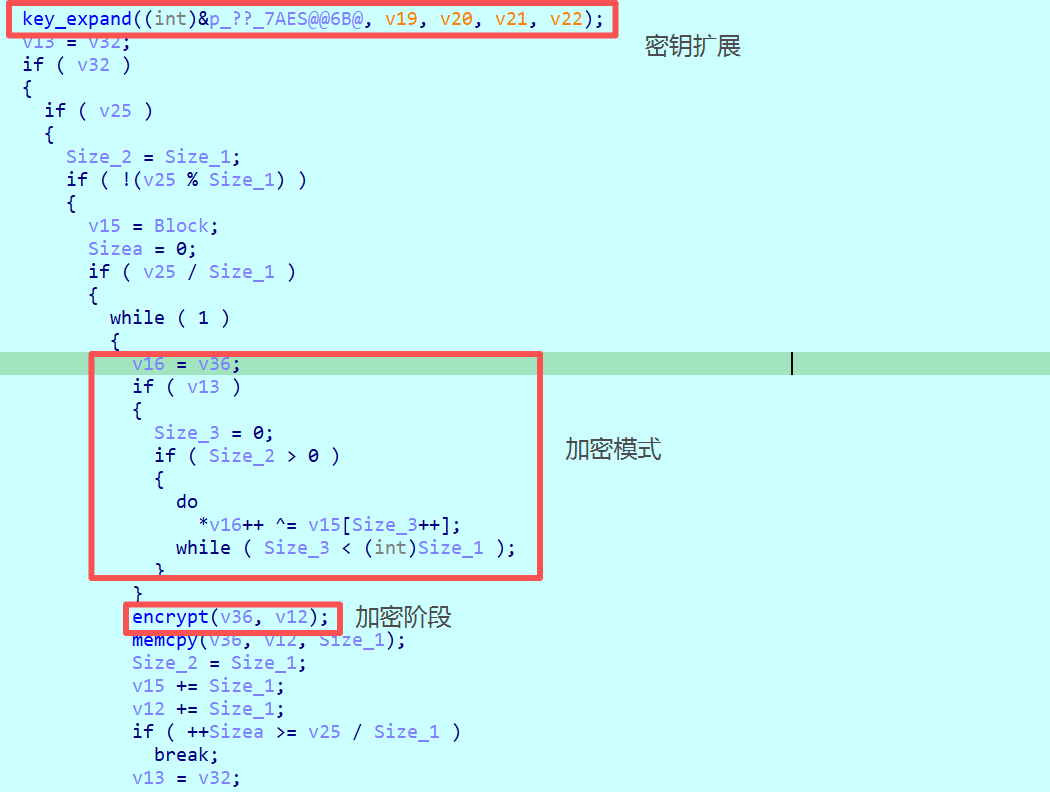
image-20251115223423002

在密鑰擴展期間還存在IV向量的拷貝過程，因此也驗證了上述猜測的CBC加密模式。

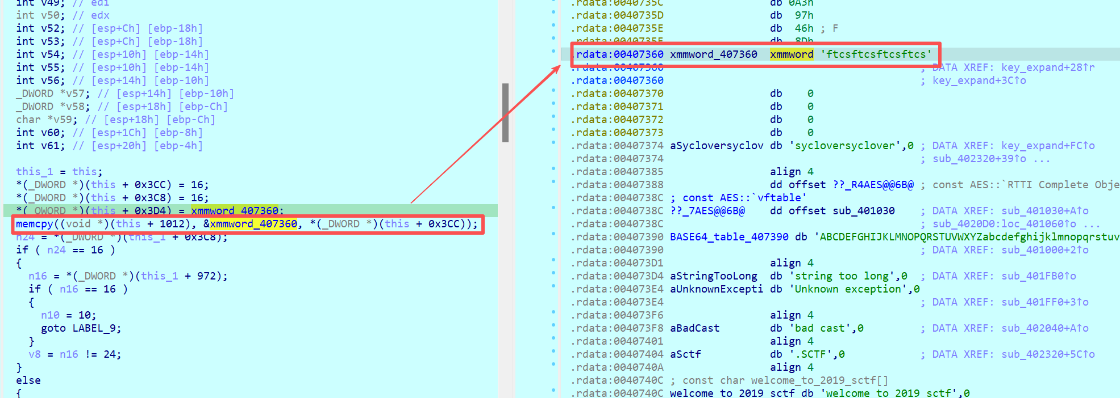
image-20251115223547789

總結

AES算法是常見的對稱加密算法，若熟悉其中的加密流程，也可以極大節約逆向的時間。

識別AES算法可以通過下述條件進行大致分析

  • 密鑰擴展的循環次數

  • S盒

  • 第十輪的加密流程

參考連接

白盒AES算法詳解(一)：https://bbs.kanxue.com/thread-280335.htm

tiny-AES-c：https://github.com/kokke/tiny-AES-c

 

更多網安技能的在線實操練習，請點擊這裏>>

網絡安全
user avatar
0 位用戶收藏了這個故事！

發佈 評論

Some HTML is okay.