1 什麼是數據結構
1.1 數據結構基本概念
數據(data) 是對客觀事物的符號表示,在計算科學中是指所有能輸入到計算機中並被計算機程序處理的符號的總稱問題。圖像、聲音等都可以通過編碼從而歸入到數據的範疇。
數據元素(data element) 是數據的基本單位,在計算機中通過作為一個整體進行考慮和處理。一個數據元素可以由若干個數據項(data item)組成。
數據對象(data object) 是性質相同的數據元素的集合,是數據的一個子集。
數據結構(data structure) 是相互之間存在一種或多種特定關係的數據元素的集合。從學科角度,數據結構是一門研究非數值計算的程序設計問題中計算機的操作對象以及它們之間的關係和操作等的學科。
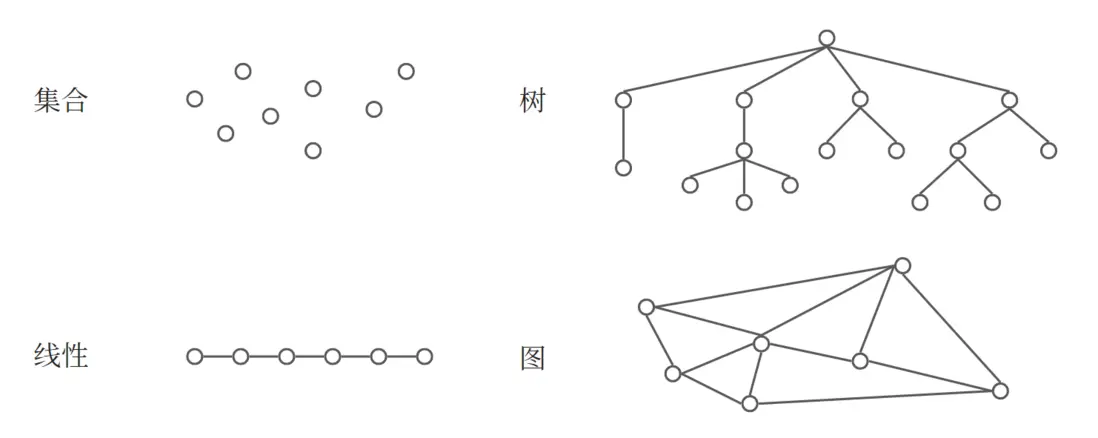
在任何問題中,數據元素都不是孤立存在的,而是在他們之間存在某種關係,這種數據元素之間的關係稱為結構(structure)。根據數據元素之間關係的不同特性,通常有以下 4 種基本結構:
- 集合:結構中的數據元素除了同屬一個集合的關係外,無其他關係。
- 線性結構:結構中的數據元素之間存在一個對一個的關係。
- 樹形結構:結構中的數據元素之間存在一個對多個的關係。
- 圖狀結構或網狀結構:結構中的數據元素之間存在多個對多個的關係。
1.2 數據結構的形式定義
數據結構的形式定義:
數據結構是一個二元組:
$$ Data\_ Structure = (D, S) $$
其中,$D$ 是數據元素的集合,$S$ 是 $D$ 上關係的有限集。
例如,複數是一種數據結構:
$$ Complex = (C, R) $$
其中,C 是兩個實數的集合 {c1, c2},R={P},而 P 是定義在集合 C 上的一張關係 {<c1, c2>},其中有序偶 <c1, c2> 表示 c1 是複數的實部,c2 是複數的虛部。
結構定義中的“關係”描述的是數據元素之間的邏輯關係,因此又稱為數據的邏輯結構。
1.3 數據結構的計算機表示
數據結構在計算機中的表示(又稱映像)稱為數據的物理結構,又稱存儲結構,它包括數據元素的表示和關係的表示。計算機中表示信息的最小單位是二進制的位(bit),可以用若干個位組合起來形成一個位串表示一個數據元素(如用 8 位二進制表示一個字符),通常稱這個位串為元素(element)或結點(node)。當數據元素由若干個數據項組成時,位串中對應於各個數據項的子位串稱為數據域(data field)。因此,元素或結點可以看做數據元素在計算機中的映射。
數據元素之間的關係在計算機中有兩種不同的表示方法:
- 順序映像:藉助元素在存儲器中的相對位置來表示元素之間的邏輯關係。
- 非順序映像:藉助指示元素存儲地址的指針表示元素之間的邏輯關係。
由此得到兩種不同的存儲結構:順序存儲結構和鏈式存儲結構。
注意:任何一個算法的設計取決於選定的數據(邏輯)結構,而算法的實現依賴於採用的存儲結構。
存儲結構涉及數據元素及其關係在存儲器中的物理位置,從高級程序語言的角度,可以借用高級程序語言中提供的“數據類型”來描述它,例如,可以使用一維數組來描述順序存儲結構,用 C 語言提供的指針來描述聯賽存儲結構。
1.4 數據類型、抽象數據類型和多形數據類型
數據類型(data type) 是一個值的集合和定義在這個值集上的一組操作的總稱,是一個和數據結構密切相關的概念,最早出現在高級編程語言中,用來刻畫(程序)操作對象的特性。按“值”的不同特性,高級程序語言中的數據類型可分為兩類:
- 原子型:非結構的,不可拆解的,如 C 語言中的基本類型(整型、實型、字符型、枚舉類型)、指針類型和空類型。
- 結構類型:由若干個成分按某種結構組成,是可分解的,其成分可以是非結構的,也可以是結構的,如數組。
抽象數據類型(abstract data type,簡稱 ADT) 是指一個數學模型以及定義在該模型上的一組操作抽象數據類型的定義仍取決於它的一組邏輯特性,而與其在計算機內部如何表示和實現無關,無論其內部結構如何變化,只要它的數學特性不變,都不影響其外部使用。
抽象數據類型和數據類型實際上是一個概念,“抽象”的意義在於數據類型的數學抽象特性。另一方面,抽象數據類型的範疇更廣,它不再侷限於各處理器中已定義並實現的數據類型(固有數據類型),還包括用户在設計軟件系統時自己定義的數據類型。
注意:一個軟件系統的框架應建立的數據之上,而不是建立在操作之上。
一個含抽象數據類型的軟件模塊通常應包含定義、表示和實現 3 個部分。抽象數據類型的定義由一個值域和定義在該值域上的一組操作組成。若按其值的不同特性,可細分為 3 種類型:
- 原子類型(atomic data type):屬於該類型的變量的值不可分解,一般情況下已有的固有數據類型足以滿足需求,較少用。
- 固定聚合類型(fixed-aggregate data type):屬於該類型的變量的值由確定數目的成分按照某種結構組成。如複數由連個實數依確定的次序組成。
- 可變聚合類型(variable-aggregate data type):和固定聚合類型比較,構成可變聚合類型的值的成分數目不確定。例如長度可變的有序整數序列。
後兩種類型統稱為結構類型。
和數據結構的形式定義相對應,抽象數據類型可用以下三元組表示:
$$ (D, S, P) $$
其中,D 是數據對象,S 是 D 上的關係集,P 是對 D 的基本操作集。
往後的介紹默認使用下面的格式定義抽象數據類型:
ADT 抽象數據類型名 {
數據對象: <數據對象的定義>
數據關係: <數據關係的定義>
基本操作: <基本操作的定義>
} ADT 抽象數據類型名其中,數據對象和數據關係的定義用偽代碼描述,基本操作的定義格式為:
基本操作名(參數表)
初始條件: <初始條件描述>
操作結果: <操作結果描述>基本操作有兩種參數:
- 賦值參數:只為操作提供輸入值。
- 引用參數:一
&開頭,除可提供輸入值外,還將返回操作結果。
“初始條件”描述了操作執行之前數據結構和參數應滿足的條件,若不滿足,則操作失敗並返回相應出錯信息。“操作結果”説明了操作正常完成之後數據結構的變化狀況和應返回的結果。若初始條件為空,則省略。
下面定義一個抽象數據類型三元組:
ADT Triplet {
數據對象: D = {e1, e2, e3 | e1, e2, e3 ∈ ElemSet}
數據關係: R1 = {<e1, e2>, <e2, e3>}
基本操作:
InitTriplet(&T, v1, v2, v3)
操作結果: 構造三元組 T,元素 v1,v2,v3 分別賦值給 e1,e2,e3
Get(T, i, &e)
初始條件: 三元組 T 已存在
操作結果: 用 e 返回 T 的第 i 元的值
Max(T, &e)
初始條件: 三元組 T 已存在
操作結果: 用 e 返回 T 的三個元素中的最大值
} ADT Triplet多形數據類型(polymorphic data type) 是指其值的成分不確定的數據類型。例如上面定義的抽象數據類型 Triplet,其元素 e1、e2、e3 可以是整數、字符或字符串,甚至是更復雜地由多種成分組成(只要能進行關係運算即可)。無論其元素具有何種特性,元素之間的關係相同,基本操作相同。從抽象數據類型的角度看,具有相同的抽象特性,因此稱為多形數據類型。顯然,多形數據類型需要藉助面向對象的程序設計語言來實現,這裏默認使用類 C 語言作為描述工具,故只討論含有確定成分的數據元素的情況,如上面例子中的 ElemSet。
2 抽象數據類型的表示與實現
抽象數據類型可通過固有數據類型來表示和實現。這裏採用類 C 語言作為描述語言,並進行了適當的擴充修改。簡要説明如下:
-
預定義常量和類型:
// 函數結果狀態代碼 #define TRUE 1 #define FALSE 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVEFLOW -2 // Status 時函數類型,其值時函數結果狀態代碼 typedef int Status; - 數據結構的表示(存儲結構)用類型定義
typedef描述,數據元素類型約定為 ElemType,由用户在使用該數據時自行定義。 -
基本操作的算法用以下形式的函數描述:
函數類型 函數名(函數參數表) { // 算法説明 語句序列 } // 函數名除了函數參數需要説明類型外,算法中使用的輔助變量可以不作變量聲明,必要時對其作註釋説明。一般 a、b、c、d、e 等用作數據元素名,i、j、k、l、m、n 等用作整型變量名,q、p、r 等用作指針變量名。當函數返回值為函數結果狀態代碼時,函數定義用
Status類型名。除了值調用方式外,增加了 C++ 語言的引用調用的參數傳遞方式,在形參表列中,以&開頭的參數即為引用參數。 -
賦值語句有:
簡單賦值 變量名 = 表達式; 串聯賦值 變量名1 = 變量名2 = ... = 變量名k = 表達式; 成組賦值 (變量名1, ..., 變量名k) = (表達式1, ... , 表達式k); 結構名 = 結構名; 結構名 = (值1, ... , 值k); 變量名[] = 表達式; 變量名[起始下標..終止下標] = 變量名[起始下標..終止下標]; 交換賦值 變量名 <-> 變量名; 條件賦值 變量名 = 條件表達式 ? 表達式T : 表達式F; -
選擇語句有:
條件語句1 if(表達式) 語句; 條件語句2 if(表達式) 語句; else 語句; 開關語句1 switch(表達式) { case 值1: 語句序列1; break; ... case 值n: 語句序列n; break; default: 語句序列n+1; } 開關語句2 switch { case 條件1: 語句序列1; break; ... case 條件n: 語句序列n; break; default 語句序列n+1; } -
循環語句有:
for語句 for(賦值表達式序列; 條件; 修改表達式序列) 語句; while語句 while(條件) 語句; do-while語句 do { 語句序列; } while(條件); -
結束語句有:
函數結束語句 return 表達式; return; case結束語句 break; 異常處理語句 exit(異常代碼); -
輸入輸出語句有:
輸入語句 scanf([格式串], 變量1, ..., 變量n); 輸出語句 printf([格式串], 表達式1, ..., 表達式n); -
註釋:
單行註釋 // 文字序列 -
基本函數有:
求最大值 max(表達式1, ..., 表達式n) 求最小值 min(表達式1, ..., 表達式n) 求絕對值 abs(表達式) 求不足整數值 floor(表達式) 求進位整數值 ceil(表達式) 判定文件結束 eof(文件變量) 或 eof 判定行結束 eoln(文件變量) 或 eoln -
邏輯運算約定:
與運算 && 或運算 ||
以抽象數據類型 Triplet 的表示和實現為例:
// 採用動態分配的順序存儲結構
typedef ElemType * Triplet; // 由 InitTriplet 分配 3 個元素存儲空間
// 基本操作的函數原型説明
Status InitTriplet(Triplet &T, ElemType v1, ElemType v2, ElemType v3);
// 操作結果:構造三元組 T,元素 v1,v2 和 v3 分別賦值給 e1,e2,e3
Status Get(Triplet T, int i, ElemType &e);
// 初始條件:三元組 T 已存在,1≤i≤3
// 操作結果:用 e 返回 T 的第 i 元的值
Status Max(Triplet T, ElemType &e)
// 初始條件:三元組 T 已存在
// 操作結果:用 e 返回 T 三個元素中的最大值
// 基本操作的實現
Status InitTriplet(Triplet &T, ElemType v1, ElemType v2, ElemType v3) {
// 構造三元組 T
T = (ElemType *) malloc (3 * sizeof(ElemType)); // 分配 3 個元素的存儲空間
if(!T) exit(OVERFLOW); // 分配存儲空間失敗
T[0] = v1; T[1] = v2; T[2] = v3;
return OK;
} // InitTriplet
Status Get(Triplet T, int i, ElemType &e) {
// 1≤i≤3,用 e 返回 T 的第 i 元的值
if(i<1 || i>3) return ERROR;
e = T[i-1];
return OK;
} // Get
Status Max(Triplet T, ElemType &e) {
// 用 e 返回 T 中最大元素的值
e = (T[0]>=T[1]) ? ((T[0]>=T[2]) ? T[0]:T[2]) : ((T[1]>=T[2]) ? T[1]:T[2])
return OK;
} // Max3 算法和算法分析
3.1 算法
算法(algorithm) 是對特定問題求解步驟的一種描述,它是指令的有限序列,其中每一條指令表示一個或多個操作。此外,一個算法還具有下列 5 個重要特性:
- 有窮性:一個算法必須總是(對任何合法的輸入值)在執行有窮步之後結束,且每一步都可在有窮時間內完成。
- 確定性:算法中每一條指令必須有確切的含義,讀者理解時不會產生二義性。並且,在任何條件下,算法只有惟一的一條執行路徑,即對於相同的輸入只能得出相同的輸出。
- 可行性:一個算法是能行的,即算法中描述的操作都是可以通過已經實現的基本運算執行有限次來實現的。
- 輸入:一個算法有零個或多個的輸入,這些輸入取自於某個特定的對象的集合。
- 輸出:一個算法有一個或多個的輸出,這些輸出是同輸入有着某些特定關係的量。
3.2 算法設計的要求
一個好的算法應考慮達到以下目標:
- 正確性:算法要滿足具體問題的要求。
- 可讀性:便於理解、調試和修改。
- 健壯性:當輸入非法數據時能夠做出適當的反應或處理,而不是參數不合理的輸出結果。
- 效率與低存儲量需求:效率涉及程序運行時間,低儲存量涉及程序運行時所需要的最大存儲空間。
3.3 算法效率的度量
度量一個程序的運行時間通常有兩種方法:
- 事後統計:利用計算機內部的計時功能,不同的算法程序可通過一組或若干組相同的統計數據以分辨優劣。
缺陷:必須先運行依據算法編制的程序;所得時間的統計量依賴於計算機的軟件、硬件等環境因素,有時容易掩蓋算法本身優劣。 -
事前分析估算:一個用高級程序語言編寫的程序在計算機上運行所消耗的時間取決於以下因素:
- 依據的算法選用的策略;
- 問題的規模;
- 書寫程序的語言:語言級別越高,執行效率越低;
- 編譯程序所產生的的機器代碼的質量;
- 機器執行指令的速度。
由此,使用絕對時間衡量算法的效率是不合適的。拋開計算機軟件、硬件因素,可認為一個特定算法的效率只依賴於問題的規模(通常用整數 n 表示),或者説,它是問題規模的函數。
一個算法由控制結構和原操作(固有數據類型的操作)構成,算法時間取決於兩者的綜合效果。為了便於比較同一問題的不同算法,通常的做法是:從算法中選取一種對所研究的問題(或算法類型)來説是基本操作的原操作,以該基本操作重複執行的次數作為算法的時間量度。
時間複雜度:一般情況下,算法中基本操作重複執行的次數是問題規模 n 的某個函數 f(n),算法的時間量度記作:
$$ T(n) = O(f(n)) $$
它表示隨問題規模 n 的增大,算法執行時間的增長率和 $f(n)$ 的增長率相同,稱為算法的漸近時間複雜度(asymptotic time complexity),簡稱時間複雜度。
O 的形式定義:若 $f(n)$ 是正整數 n 的一個函數,則 x_n=O(f(n)) 表示存在一個正的常數 M,使得當 n ≥ n0 時都滿足 |xn| ≤ | M(f(n)) |。
顯然,被稱做問題的基本操作的原操作應是其重複執行次數和算法的執行時間成正比的原操作,多數情況下它是最深層循環內的語句中的原操作,它的執行次數和包含它的語句的頻度相同。語句的 頻度(frequency count) 指的是該語句重複執行的次數。
例如,兩個 N x N 矩陣相乘的算法:
for(i=1; i<=n; ++i)
for(j=1; j<=n; ++j) {
c[i][j] = 0;
for(k=1; k<=n; ++k)
c[i][j] += a[i][k] * b[k][j];
}其中,乘法運算是矩陣相乘問題的基本操作,整個算法的執行時間與該基本操作的重複執行次數的三次方成正比,記作
$$ T(n) = O(n^3) $$
常見的時間複雜度如 \( O(1) \)、\( O(n)\)、\(O(n^2)\) 等分別稱為常量階、線性階、平方階,此外還有對數階 \( O(\log n) \)、指數階 \( O(2^n) \) 等。考慮到不同數量級的複雜度性狀,應儘可能地選用多項式階 \( O(n^k)\) 的算法,而不是使用指數階的算法。
一般情況下,對一個問題(或一類算法)只需選擇一種基本操作來討論算法的時間複雜度即可,有時也需要考慮幾種基本操作,甚至可以對不同的操作賦予不同的權值。
由於算法的時間複雜度只考慮問題規模 n 的增長率,因此,在難以精確計算基本操作的執行次數(或語句的頻度)的情況下,只需求出它關於 n 的增長率或階即可。如下面的程序:
for(i=2; i<=n; ++i)
for(j=2; j<=i-1; ++j) {
++x;
a[i][j] = x;
}語句 ++x 的執行次數關於 n 的增長率為 \( n^2\),它是語句頻度表達式 \( (n-1)(n-2)/2\) 中增長最快的項。
有的情況下,算法中基本操作的重複執行次數還隨輸入的數據集的不同而不同,如起泡排序算法:
void bubble_sort(int a[], int n) {
// 將 a 中整數序列由小到大重新排列
for(i=n-1,change=TRUE; i>=1&&change; --i) {
change = FALSE;
for(j=0; j<i; ++j) {
if(a[j] > a[j+1]) {
a[j] <-> a[j+1];
change = TRUE;
}
}
}
} // bubble_sort上面程序中的基本操作為 a[j]<->a[j+1],當 a 的初始序列為由小到大排列時,基本操作執行次數為 0,當 a 初始序列為由大到小排列時,基本操作執行次數為 \(n(n-1)/2\)。對這類算法的分析,有兩種解決方法:
- 考慮所有可能輸入數據集的期望值,此時相應的時間複雜度為算法的平均時間複雜度。
- 討論算法在最壞情況下的時間複雜度,即估算算法執行時間的上界。
假設 a 初始輸入數據可能出現 \(n!\) 種排列情況的概率相等,則起泡排序額算法的時間複雜度為 \(T_{arg}(n)=O(n^2)\)。起泡排序算法的最壞情況為 a 中初始序列為由大到小排列,則起泡排序算法在最壞情況下的時間複雜度為 \(T(n)=O(n^2)\)。
很多情況下各種輸入數據出現的概率難以確定,因此通常第二種方法更加可行。往後討論的時間複雜度均默認為最壞情況下的時間複雜度。
3.4 算法的存儲空間需求
類似於算法的時間複雜度,以 空間複雜度(space complexity) 作為算法所需存儲空間的量度:
$$ S(n) = O(f(n)) $$
其中,n 為問題的規模。
一個上機執行的程序除了需要存儲空間來寄存本身所用指令、常數、變量和輸入數據外,也需要一些對數據進行操作的工作單元和存儲一些為實現計算所需信息的輔助空間。若輸入數據所佔空間只取決於問題本身,和算法無關,則只需要分析除輸入和程序之外的額外空間,否則應同時考慮輸入本身所需空間(和輸入數據的表示形式有關)。若額外空間相對於輸入數據量來説是常數,則稱此算法為原地工作。如果所佔空間量依賴於特定的輸入,則除特別指明外,均按最壞情況來分析。
Reference:
嚴蔚敏 / 吳偉民《數據結構(C語言版)》