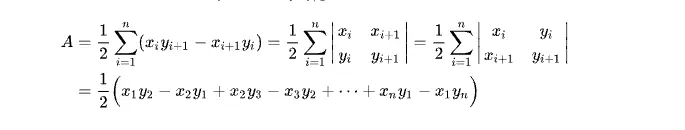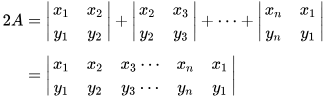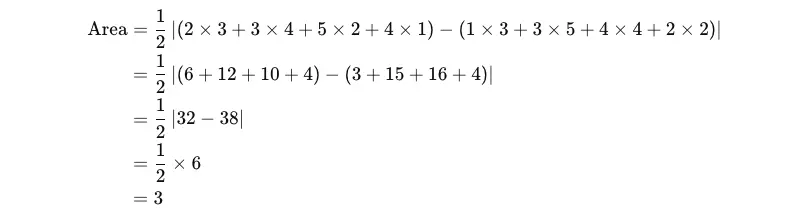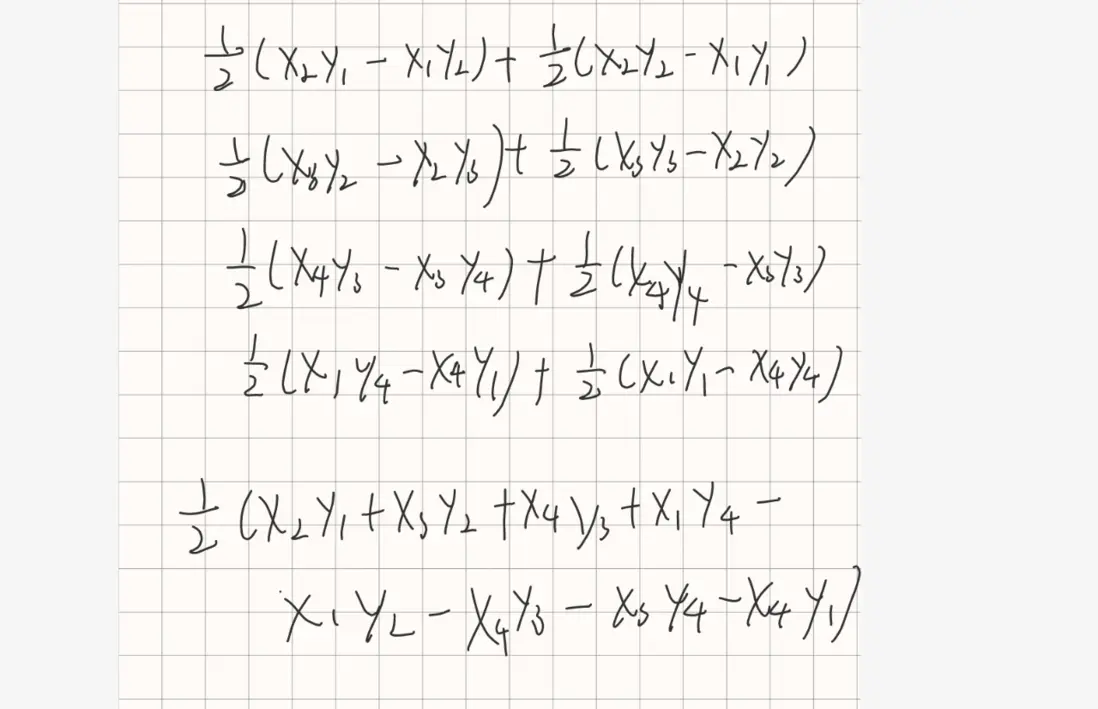基於高斯面積公式計算多邊形面積和圖像透視變換切片實現詳情 - python3.x,opencv kexb 博客

前言

當前有一個需求，在之前進行對進行發票設別標註的時候遇到的痛點，那就是需要用户下載指定環境，而且有很多小毛病，無疑是增加了工作量。在這個基礎上，就決定自己在web進行圖像標註，由web端進行畫框進行標圖進行保存四個座標，根據之後再根據四個座標進行圖像切片。基於此就有了這個文章，本文將介紹如何使用高斯面積公式（也稱為Shoelace公式）計算多邊形的有向面積，並結合圖像處理技術對圖像進行旋轉裁剪。

裁剪的圖片

實現的效果

實現步驟

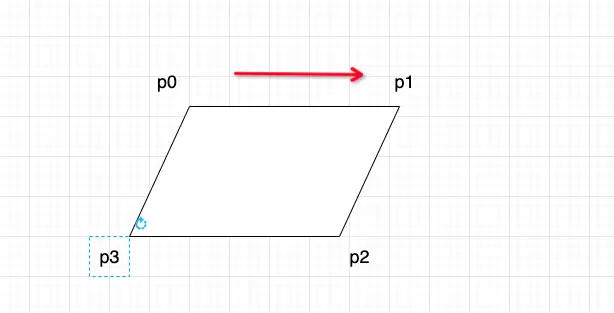
計算多邊形的有向面積：利用高斯面積公式計算多邊形的有向面積。如果面積為負，説明頂點是按逆時針順序排列的，需要進行調整以確保順時針順序。
計算裁剪圖像的寬度和高度：根據調整後的頂點座標，計算旋轉裁剪後圖像的寬度和高度。
執行旋轉裁剪：使用計算得到的寬度和高度，對圖像進行旋轉裁剪。

計算多邊形的有向面積

 d = 0.0
    # 使用高斯面積公式計算多邊形的有向面積
    for index in range(-1, 3):
        d += -0.5 * (points[index + 1][1] + points[index][1]) * (
                points[index + 1][0] - points[index][0])
        # 如果面積為負，交換點的位置以確保順時針順序
    if d < 0:
        tmp = np.array(points)
        points[1], points[3] = tmp[3], tmp[1]

為什麼要確保為順時針,這是因為我們需要計算固定長和寬

順時針的情況

逆時針的情況

高斯面積公式

Shoelace公式（也稱為高斯面積公式或鞋帶公式）是一個用於計算二維平面上簡單多邊形面積的算法。這個公式的基本思想是將多邊形的頂點視為平面上的點，並通過這些點的座標來計算多邊形的面積。

高斯面積公式

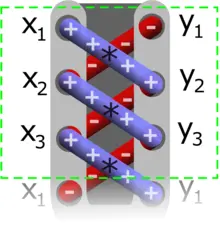
鞋帶公式

長的很像鞋帶
為什麼叫做鞋帶公式，這是因為在計算的過程很像鞋帶一樣纏繞着，

鞋帶公式是這樣子算的：

鞋帶公式多邊形面積計算

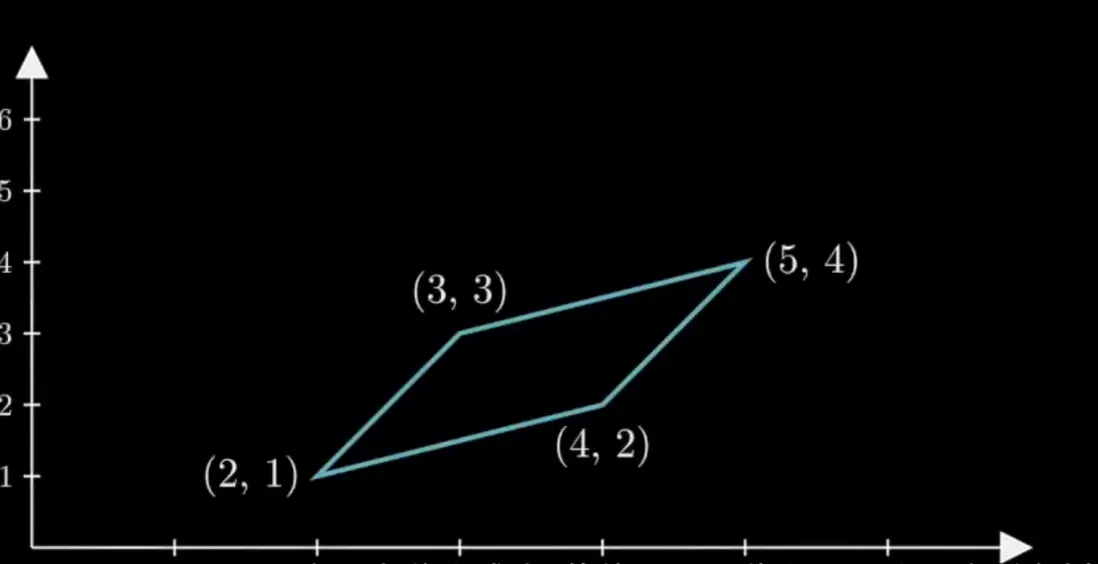
比如一個多邊形（四角形），

P1(x1,y2)=(2,1),P2(x2,y2)=(3, 3),P3(x3,y3)=(5, 4),P4(x4,y4)=(4, 2)

可得面積：

為什麼要加絕對值，這就是涉及到高斯面積公式的推理過程，結合這個多邊形案例

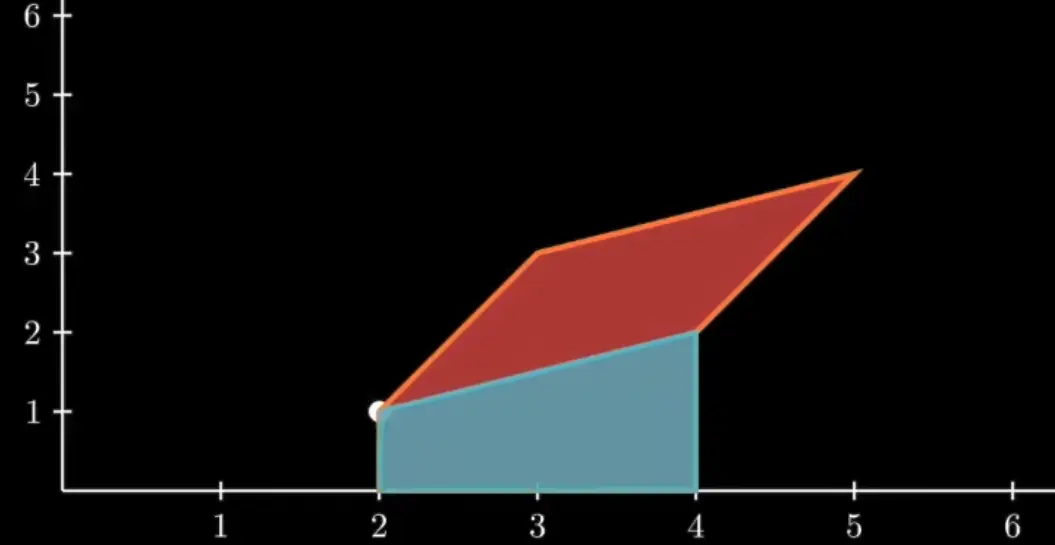
梯形公式

計算P1到P2的面積

 (x1, y1) = (2, 1) (x2, y2) = (3, 3)
 2/(x2y1 - x1y2） + 2/(x2y2-x1y1) 
 area = 2

計算P2 到 P3梯形面積

 (x2, y2) = (3, 3) (x3, y3) = (5, 4)
 2/(x3y2 - x2y3） + 2/(x3y3-x2y2) 
 area = 7

計算P3 到 P4 梯形面積
這裏發現當前的x4-x3 當x3大於x4時，計算的梯形面積為負數

 (x3, y3) = (5, 4) (x4, y4) = (4, 2)
 2/(x4y3 - x3y4） + 2/(x4y4-x3y3) 
 are = -3

計算x4y4 x1y1 梯形面積
這裏發現當前的x1-x4 當x4大於x1時，計算的梯形面積為負數

 (x1, y1) = (2, 1) (x4, y4) = (4, 2)
 2/(x1y4 - x4y1） + 2/(x1y1-x4y4) 
 area = -3

最後相加可得高斯面積公式

根據面積相加可得

 area1 + area2 + area3 + area4 = area
 2 + 7 - 3 -3 = 3

使用勾股定理計算圖像長和寬

    [0, 0],[4, 0],[4, 3], [0, 3]
    # 計算裁剪圖像的寬度
    img_crop_width = int(
        max(
             # 勾股定理
            np.linalg.norm(points[0] - points[1]), # 距離 (0,0) 到 (4,0)
            np.linalg.norm(points[2] - points[3]))) # 距離 (4,3) 到 (0,3)
    # 計算裁剪圖像的高度
    img_crop_height = int(
        max(
            np.linalg.norm(points[0] - points[3]),  # 距離 (0,0) 到 (0,3)
            np.linalg.norm(points[1] - points[2]))) # 距離 (4,0) 到 (4,3)
    pts_std = np.float32([[0, 0], [img_crop_width, 0],
                              [img_crop_width, img_crop_height],
                              [0, img_crop_height]])

手動計算

得到長和框、裁剪四個座標

    img_crop_width: 4, img_crop_height: 3
    pts_std = [[0. 0.]  [4. 0.][4. 3.][0. 3.]]

執行旋轉裁剪

    # 獲取透視變換矩陣
        M = cv2.getPerspectiveTransform(points, pts_std)
        # 進行透視變換
        dst_img = cv2.warpPerspective(
            img,
            M, (img_crop_width, img_crop_height),
            borderMode=cv2.BORDER_REPLICATE,
            flags=cv2.INTER_CUBIC)
        # 獲取變換後圖像的高度和寬度
        dst_img_height, dst_img_width = dst_img.shape[0:2]
        # 如果高度和寬度的比例大於等於1.5，則旋轉圖像
        if dst_img_height * 1.0 / dst_img_width >= 1.5:
            dst_img = np.rot90(dst_img)

獲取透視變換矩陣

M = cv2.getPerspectiveTransform(points, pts_std)

cv2.getPerspectiveTransform(points, pts_std) 計算並返回一個 3x3 的透視變換矩陣 M。
points 是原始圖像中四個點的座標。
pts_std 是目標圖像中對應四個點的座標。

透視變換矩陣 M 用於將原始圖像中的四個點映射到目標圖像中的四個點。

poinst = np.float32([[260, 100], [600, 100], [260, 400], [600, 400]])
pts_std = np.float32([[0, 0], [600, 0], [0, 600], [600, 600]])

進行透視變換

dst_img = cv2.warpPerspective(
    img,
    M, (img_crop_width, img_crop_height),
    borderMode=cv2.BORDER_REPLICATE,
    flags=cv2.INTER_CUBIC)

cv2.warpPerspective ，它會根據你提供的變換矩陣，把圖片中的某些部分拉伸、壓縮或扭曲到你希望的位置。
img 是輸入的原始圖像。
M 是透視變換矩陣。
(img_crop_width, img_crop_height) 指定輸出圖像的大小。
borderMode=cv2.BORDER_REPLICATE 當變換過程中有些像素點移到圖像邊界外時，使用邊緣的像素顏色填充這些位置。

示例完整代碼

# 進行切片和旋轉
def get_rotate_crop(img, points):
    d = 0.0
    # 使用高斯面積公式計算多邊形的有向面積
    for index in range(-1, 3):
        d += -0.5 * (points[index + 1][1] + points[index][1]) * (
                points[index + 1][0] - points[index][0])
        # 如果面積為負，交換點的位置以確保順時針順序
    if d < 0:
        tmp = np.array(points)
        points[1], points[3] = tmp[3], tmp[1]

    try:
        # 計算裁剪圖像的寬度
        img_crop_width = int(
            max(
                np.linalg.norm(points[0] - points[1]),
                np.linalg.norm(points[2] - points[3])))
        # 計算裁剪圖像的高度
        img_crop_height = int(
            max(
                np.linalg.norm(points[0] - points[3]),
                np.linalg.norm(points[1] - points[2])))
        # 標註的目標座標
        pts_std = np.float32([[0, 0], [img_crop_width, 0],
                              [img_crop_width, img_crop_height],
                              [0, img_crop_height]])
        # 獲取透視變換矩陣
        M = cv2.getPerspectiveTransform(points, pts_std)
        # 進行透視變換
        dst_img = cv2.warpPerspective(
            img,
            M, (img_crop_width, img_crop_height),
            borderMode=cv2.BORDER_REPLICATE,
            flags=cv2.INTER_CUBIC)
        # 獲取變換後圖像的高度和寬度
        dst_img_height, dst_img_width = dst_img.shape[0:2]
        # 如果高度和寬度的比例大於等於1.5，則旋轉圖像
        if dst_img_height * 1.0 / dst_img_width >= 1.5:
            dst_img = np.rot90(dst_img)
        return dst_img
    except Exception as e:
        print(e)

參考文章

https://en.wikipedia.org/wiki/Shoelace_formula
https://waiterxiaoyy.github.io/2020/03/20/%E9%9E%8B%E5%B8%A6%...

kexb 博客

kexb 博客

博客 / 詳情