原文參考我的公眾號文章 梳理一波「二叉樹

二叉樹

二叉樹，顧名思義，每個節點最多有兩個“叉”，也就是兩個子節點，分別是左子節點和右子節點。不過，二叉樹並不要求每個節點都有兩個子節點，有的節點只有左子節點，有的節點只有右子節點。

• 根節點：無父節點的節點
• 葉子結點：無子節點的節點
• 兄弟節點：有相同根節點的節點

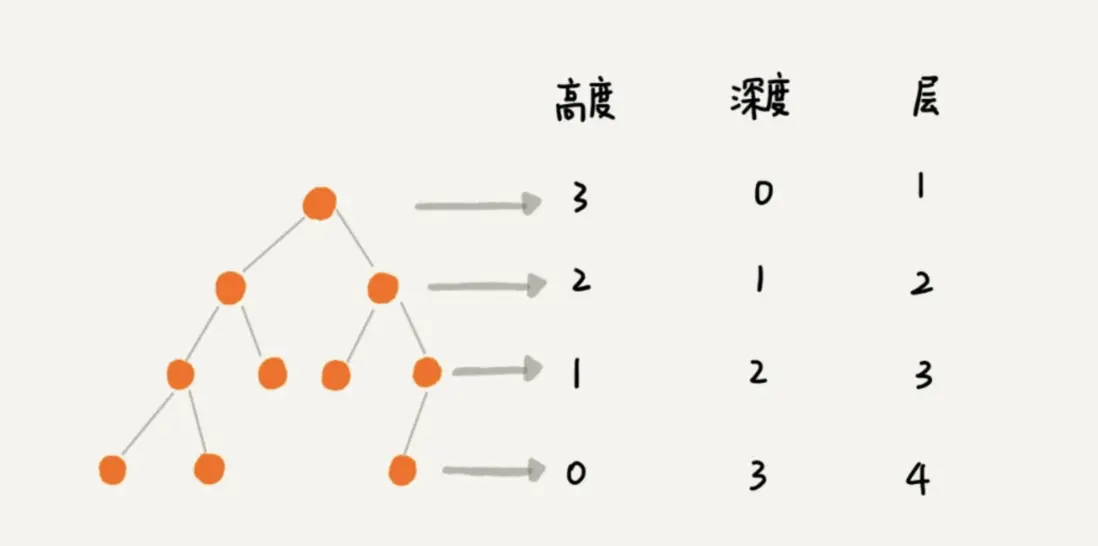
關於“樹”，還有三個比較相似的概念：高度（Height）、深度（Depth）、層（Level）。它們的定義是這樣的：

二叉查找（排序）樹

• 也叫二叉搜索樹，支持動態數據集合的快速插入、刪除、查找操作；
• 有序二叉樹：在樹中的任意一個節點，其左子樹中的每個節點的值，都要小於這個節點的值，而右子樹節點的值都大於這個節點的值；
• 是一顆二叉樹，每個節點最多兩個子結點，即每一層最多 2^(level - 1)個節點；

樹結構

/** 樹節點 */
class BinaryNode {
  constructor(data) {
    this.data = data; //存儲的數據
    this.left = null; //左節點
    this.right = null; //右節點
    this.level = 1; //所屬層級
    this.count = 1; //重複數據次數
    this.isDeleted = false; //是否被刪除
  }
}

/** 二叉樹 */
class BinarySearchTree {
  constructor() {
    this.root = null; //根節點：在第一次insert時會被賦予值
    this.nodes = 0; //節點數
    this.list = []; //遍歷二叉樹時臨時存儲數據的數組
  }
}

插入節點

插入規則：新結點值與當前插入位置（從根節點開始）的節點值進行比較

• 小於父節點值：插在父節點左節點上；
• 大於父節點值：插在父節點右節點上；
• 等於父節點值：父節點 count++；（這種方式看情況，如果結點還有其他數據而非只有一個 data，那可以。否則應合併到上一種情況，合併到右節點上）
• 插入過程可增加被插入的結點所屬 level 的維護！

// class BinarySearchTree { ... }

  /**
   * 插入數據
   * @param {*} data 結點的值
   */
  insert(data) {
    this.nodes++;

    // 遞歸插入
    // let newNode = new BinaryNode(data);
    // if (this.root === null) {
    //   this.root = newNode;
    // } else {
    //   this._insert(this.root, newNode);
    // }

    // 循環插入
    this.loopInsert(data)
  }

  /**
   * 遞歸的方式插入節點：新結點值與當前插入位置（從根節點開始）的節點值進行比較
   * 小於根節點值：插在根節點左節點上；
   * 大於等於根節點值：插在根節點右節點上；
   * 增加結點所屬level的維護！
   * @param {*} theRootNode 被插入位置節點（從根節點開始）
   * @param {*} newNode 新插入的節點
   */
  _sameValAsBigInsert(theRootNode, newNode) {
    newNode.level++; //從根出發，每執行一次_sameValAsBigInsert，層級便自動+1
    if (theRootNode.data > newNode.data) {
      if (theRootNode.left === null) {
        theRootNode.left = newNode;
      } else {
        // 説明不是葉子結點，繼續向下層插入判斷
        this._sameValAsBigInsert(theRootNode.left, newNode);
      }
    } else {
      if (theRootNode.right === null) {
        theRootNode.right = newNode;
      } else {
        // 説明不是葉子結點，繼續向下層插入判斷
        this._sameValAsBigInsert(theRootNode.right, newNode);
      }
    }
  }

  /**
   * !!!值相同，則合併到當前根節點
   * @param {*} theRootNode 被插入位置節點（從根節點開始）
   * @param {*} newNode 新插入的節點
   */
  _sameValMergeInsert(theRootNode, newNode) {
    newNode.level++; //從根出發，每執行一次_sameValMergeInsert，層級便自動+1
    if (theRootNode.data > newNode.data) {
      if (theRootNode.left === null) {
        theRootNode.left = newNode;
      } else {
        // 説明不是葉子結點，繼續向下層插入判斷
        this._sameValMergeInsert(theRootNode.left, newNode);
      }
    } else if (theRootNode.data < newNode.data) {
      if (theRootNode.right === null) {
        theRootNode.right = newNode;
      } else {
        // 説明不是葉子結點，繼續向下層插入判斷
        this._sameValMergeInsert(theRootNode.right, newNode);
      }
    } else {
      theRootNode.count++; // 值相同，則合併到當前根節點
    }
  }

   /**
   * 循環的方式插入
   * @param {*} data
   * @returns
   */
  loopInsert(data) {
    if (this.root == null) {
      this.root = new BinaryNode(data);
      return;
    }

    let p = this.root;
    while (p != null) {
      if (data > p.data) {
        if (p.right == null) {
          p.right = new BinaryNode(data);
          return;
        }
        p = p.right;
      } else {
        // data <= p.data
        if (p.left == null) {
          p.left = new BinaryNode(data);
          return;
        }
        p = p.left;
      }
    }
  }

遍歷樹（前序、中序、後續）

遍歷樹採取遞歸的方式，出遞歸的條件是 node=null

  /** 遍歷樹: [type] 遍歷方式 */
  print(type) {
    this.list = [];
    let callee = `${type}Order`;
    this[callee](this.root);
  }

• 前序遍歷

prevOrder(node){
    if(node==null){
        return
    }
    console.log(node.data)
    this.prevOrder(node.left)
    this.prevOrder(node.right)
}

• 中序遍歷（遍歷結果正好是有序的）

inOrder(node){
    if(node==null){
        return
    }
    this.inOrder(node.left)
    console.log(node.data)
    this.inOrder(node.right)
}

• 後序遍歷

postOrder(node){
    if(node==null){
        return
    }
    this.postOrder(node.left)
    this.postOrder(node.right)
    console.log(node.data)
}

查找節點

先取根節點，如果它等於我們要查找的數據，那就返回。如果要查找的數據比根節點的值小，那就在左子樹中遞歸查找；如果要查找的數據比根節點的值大，那就在右子樹中遞歸查找。

  /**
   * 查找一個節點
   * @param {*} data 要查找的值
   * @returns
   */
  find(data) {
    let node = this.root;
    while (node != null) {
      if (data < node.data) {
        node = node.left;
      } else if (data > node.data) {
        node = node.right;
      } else {
        return node;
      }
    }

    return null;
  }

刪除節點

物理刪除：刪除操作比較複雜，一般要分以下三種情況分別處理。

• 被刪除節點沒有子節點：直接將父節點中，指向要刪除節點的指針置為 null；
• 被刪除節點只有一個子節點：只需要更新父節點中，指向要刪除節點的指針，讓它指向要刪除節點的子節點（左或右）就可以了；
• 被刪除節點右兩個子節點（最複雜）：我們需要找到這個節點的右子樹中的最小節點，把它替換到要刪除的節點上。然後再刪除掉這個最小節點，因為最小節點肯定沒有左子節點（如果有左子結點，那就不是最小節點了），所以，我們可以應用上面兩條規則來刪除這個最小節點；

邏輯刪除節點（簡易版）

  /**
   * 刪除節點（簡易版）
   * 對要刪除的節點做標記，表示已刪除
   * @param {*} data
   */
  delete(data){
    let targetNode = this.find(data);
    // 未找到要刪除的數據
    if(targetNode == null){
        return null
    }
    // 標記為“已刪除”
    targetNode.isDeleted = true;
  }
}

邏輯刪除對應的樹遍歷方式修改！

  prevOrder(node) {
    if (node == null) {
      return;
    }
    /**+++ 此處增加判斷，inOrder和postOrder同樣處理！ */
    if (node.isDeleted != true) {
      this.list.push(node.data);
      console.log(node.data);
    }
    this.prevOrder(node.left);
    this.prevOrder(node.right);
  }

測試有序二叉樹

// 創建一顆有序二叉樹
let bsTree = new BinarySearchTree();

// 插入數據
let arr = [6,8,7,6,3,5,9,4]
arr.map(item=>{
    bsTree.insert(item)
})

// 二叉樹結構
console.log(bsTree);

// 三種方式遍歷整棵樹！
console.log('前序遍歷');
bsTree.prevOrder(bsTree.root)
console.log('\n\n')
console.log('中序遍歷（有序輸出）');
bsTree.inOrder(bsTree.root)
console.log('\n\n')
console.log('後序遍歷');
bsTree.postOrder(bsTree.root)
console.log('\n\n')

// 查找某個節點
console.log("\n查找值6");
console.log(bsTree.find(6));

// 刪除某個節點
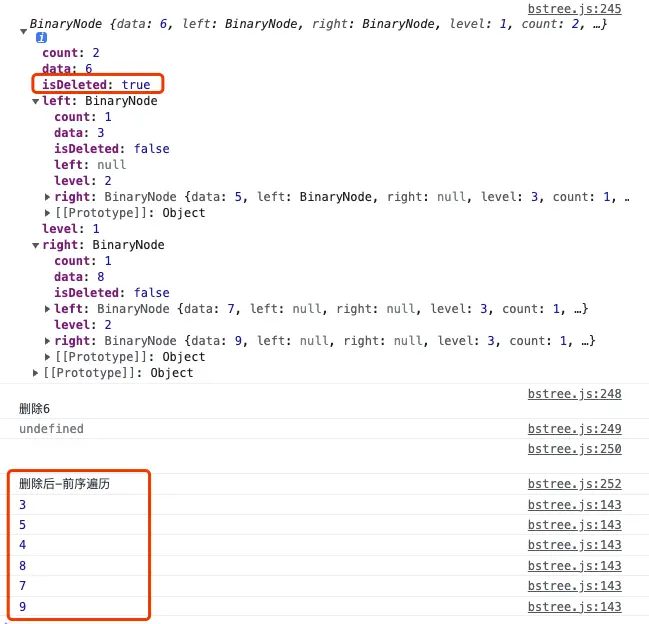
console.log("\n刪除6");
console.log(bsTree.delete(6));
console.log("\n\n");

console.log("刪除後-前序遍歷");
bsTree.print("prev");

總結（來自極客時間課程總結，總歸比我自己總結的好 🤷‍♂️）

這篇文章學習了一種特殊的二叉樹，二叉查找樹。它支持快速地查找、插入、刪除操作。

二叉查找樹中，每個節點的值都大於左子樹節點的值，小於右子樹節點的值。不過，這只是針對沒有重複數據的情況。對於存在重複數據的二叉查找樹，我介紹了兩種構建方法，

• 一種是讓每個節點存儲多個值相同的數據；
• 另一種是，每個節點中存儲一個數據。針對這種情況，只需要稍加改造原來的插入、刪除、查找操作即可。

在二叉查找樹中，查找、插入、刪除等很多操作的時間複雜度都跟樹的高度成正比。兩個極端情況的時間複雜度分別是 O(n) 和 O(logn)，分別對應二叉樹退化成鏈表的情況和完全二叉樹。

參考鏈接

js 二叉樹

數據結構與算法之美-二叉樹基礎下