一個緩存結構需要實現如下功能：

void set(int key,int value)：加入或者修改 key 對應的 value

int get(int key)：查詢 key 對應的 value 值

但是緩存最多放 K 條記錄，如果新的 K + 1 條記錄需要加入，就需要根據策略刪掉一條記錄，然後才能把新記錄加入。

這個策略為：在緩存結構的 K 條記錄中，哪一個 key 從進入緩存結構的時刻開始，被調用 set 或者 get 次數最少，就刪掉這個key 的記錄；如果調用次數最少的 key 有多個，上次調用發送最早的 key 被刪除。

這個就是 LFU 緩存替換算法。實現這個結構，K 作為參數。

解法一：哈希表 + 有序表

緩存中的數據是 k,v 對，所以用 map 存儲數據。由於緩存數據需要根據：使用次數和使用時間進行淘汰，如果遍歷數據查找需要淘汰的數據，耗時比較高。因此需要維護一個有序結構，方便查找要淘汰的數據。

• 有序數組：

  • 查找要淘汰數據的耗時為：O(1)，刪除後需要移動數據，耗時為：O(K)
  • 每次操作都需要更新 count 和 time 並維護數組的有序，此時也需要查找並移動數據，耗時為為：O(K)

• 有序鏈表：

  • 查找要淘汰數據的耗時為：O(1)，（比如頭結點或者尾結點）
  • 更新操作時，查找對應節點的耗時為：O(K)

• 有序表：

  • 查找並移除要淘汰的數據的耗時為：O(log K)
  • 更新操作的耗時時為：O(log K)

• 小頂堆：

  • 查找並移除要淘汰的數據的耗時為：O(1)，移除堆頂後需要堆化的耗時為：O(log K)。
  • 更新數據後，也需要堆化，耗時為：O(log K)。

時間複雜度：O(log K)

空間複雜度：O(K)

import java.util.*;

public class LFU1 {
    public static class Node implements Comparable<Node> {
        public int key;
        public int value;
        // 這個節點發生get或者set的次數總和
        public int count;
        // 最後一次操作的時間
        public int time;
        
        public Node(int key, int value, int count, int time) {
            this.key = key;
            this.value = value;
            this.count = count;
            this.time = time;
        }

        // 緩存淘汰優先級
        // 最少使用（count 越小越容易被淘汰）
        // count 相同，時間越早越容易被淘汰（time 越小越容易被淘汰）
        @Override
        public int compareTo(Node o) {
            return count == o.count ? Integer.compare(time, o.time) : Integer.compare(count, o.count);
        }

        @Override
        public String toString() {
            return "Node{" + "key=" + key + ", value=" + value + ", count=" + count + ", time=" + time + '}';
        }
    }

    public static class LFUCache {
        // 緩存過期優先級
        TreeSet<Node> set = new TreeSet<>();
        Map<Integer, Node> map = new HashMap<>();
        int capacity;
        int time = 0; // 用來計算緩存時間

        public LFUCache(int capacity) {
            this.capacity = Math.max(capacity, 0);
        }

        public Integer get(int key) {
            if (!map.containsKey(key)) {
                return null;
            }
            Node node = map.get(key);
            set(key, node.value);
            return node.value;
        }

        public void set(int key, int value) {
            this.time += 1;
            // 更新
            if (map.containsKey(key)) {
                Node node = map.get(key);
                // 刪除再插入（node 的count 和 time 變化了，TreeSet 認為是不同的數據）
                set.remove(node);
                node.time = this.time;
                node.count++;
                node.value = value;
                set.add(node);
                map.put(key, node);
                return;
            }

            // 新增
            // 如果內存滿了，淘汰一條舊數據
            if (this.capacity == this.map.size()) {
                remove();
            }
            Node node = new Node(key, value, 1, this.time);
            map.put(key, node);
            set.add(node);
        }

        public void remove() {
            if (map.size() == 0) {
                return;
            }
            Node node = set.first();
            map.remove(node.key);
            set.remove(node);
        }
    }
}

解法二：哈希表 + 小頂堆

將有序表更換為小頂堆。

刪除數據時，heap.pop()

更新數據後，堆化：heap.heapify(node)。更新數據使得 time 和 count 變大，因此只需要從 node 節點開始向下堆化。

時間複雜度：O(log K)

空間複雜度：O(K)

import java.util.*;

public class LFU3 {
    public static class Node {
        public int key;
        public int value;
        // 這個節點發生get或者set的次數總和
        public int count;
        // 最後一次操作的時間
        public int time;

        public Node(int key, int value, int count, int time) {
            this.key = key;
            this.value = value;
            this.count = count;
            this.time = time;
        }

        @Override
        public String toString() {
            return "Node{" + "key=" + key + ", value=" + value + ", count=" + count + ", time=" + time + '}';
        }
    }


    public static class NodeComparator implements Comparator<Node> {

        // 緩存淘汰優先級
        // 最少使用（count 越小越容易被淘汰）
        // count 相同，時間越早越容易被淘汰（time 越小越容易被淘汰）
        @Override
        public int compare(Node o1, Node o2) {
            return o1.count == o2.count ? Integer.compare(o1.time, o2.time) : Integer.compare(o1.count, o2.count);
        }
    }

    public static class LFUCache {
        // 緩存過期優先級
        HeapGreater<Node> heap = new HeapGreater<>(new NodeComparator());


        Map<Integer, Node> map = new HashMap<>();
        int capacity;
        int time = 0; // 用來計算緩存時間

        public LFUCache(int capacity) {
            this.capacity = Math.max(capacity, 0);
        }

        public Integer get(int key) {
            if (!map.containsKey(key)) {
                return null;
            }
            Node node = map.get(key);
            set(key, node.value);
            return node.value;
        }

        public void set(int key, int value) {
            this.time += 1;
            // 更新
            if (map.containsKey(key)) {
                Node node = map.get(key);
                // 刪除再插入（node 的count 和 time 變化了，TreeSet 認為是不同的數據）
                node.time = this.time;
                node.count++;
                node.value = value;
                heap.heapify(node);
                map.put(key, node);
                return;
            }

            // 新增
            // 如果內存慢了，淘汰一條舊數據
            if (this.capacity == this.map.size()) {
                remove();
            }
            Node node = new Node(key, value, 1, this.time);
            map.put(key, node);
            heap.push(node);
        }

        public void remove() {
            if (map.size() == 0) {
                return;
            }
            Node node = heap.pop();
            map.remove(node.key);
        }
    }
}

加強堆的部分代碼

import java.util.*;

public class HeapGreater<T> {
    private ArrayList<T> heap;
    private HashMap<T, Integer> indexMap;
    private int heapSize;
    private Comparator<? super T> comp;

    public HeapGreater(Comparator<? super T> c) {
        heap = new ArrayList<>();
        indexMap = new HashMap<>();
        heapSize = 0;
        comp = c;
    }

    public void push(T obj) {
        heap.add(obj);
        indexMap.put(obj, heapSize);
        heapInsert(heapSize++);
    }

    public T pop() {
        T ans = heap.get(0);
        swap(0, heapSize - 1);
        indexMap.remove(ans);
        heap.remove(--heapSize);
        heapify(0);
        return ans;
    }

    private void heapInsert(int index) {
        while (comp.compare(heap.get(index), heap.get((index - 1) / 2)) < 0) {
            swap(index, (index - 1) / 2);
            index = (index - 1) / 2;
        }
    }

    public void heapify(T obj) {
        heapify(indexMap.get(obj));
    }

    private void heapify(int index) {
        int left = index * 2 + 1;
        while (left < heapSize) {
            int best = left + 1 < heapSize && comp.compare(heap.get(left + 1), heap.get(left)) < 0 ? (left + 1) : left;
            best = comp.compare(heap.get(best), heap.get(index)) < 0 ? best : index;
            if (best == index) {
                break;
            }
            swap(best, index);
            index = best;
            left = index * 2 + 1;
        }
    }

    private void swap(int i, int j) {
        T o1 = heap.get(i);
        T o2 = heap.get(j);
        heap.set(i, o2);
        heap.set(j, o1);
        indexMap.put(o2, i);
        indexMap.put(o1, j);
    }
}

解法三：哈希表 + 二維雙向鏈表

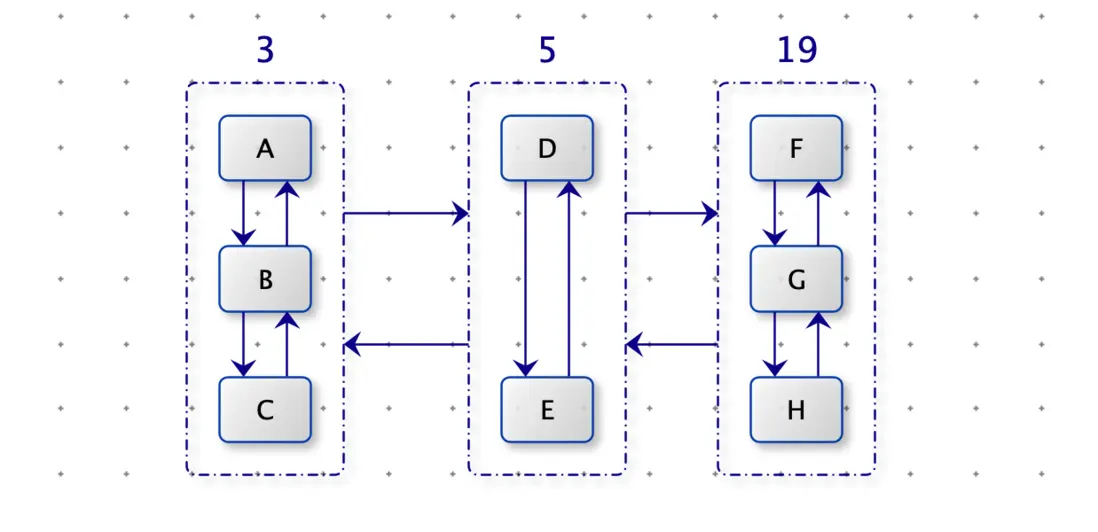
如下圖就是一個二維雙向鏈表。桶與桶之間是雙向鏈表，桶內有一個雙向鏈表。桶內雙向鏈表上的數據擁有相同的操作次數，越靠近頭部的數據，操作時間越近（從鏈表頭部插入新數據，那麼要過期數據從尾部移除）。所以要過期一個數據，刪除操作數最小的桶（頭桶）中鏈表的尾節點。

下圖演示了桶之間鏈表和桶內鏈表的變化過程。

<font color=red>原則：缺少操作數的桶，就新建桶。節點移走後出現空桶，將空桶刪除。注意在這個過程中保持：桶之間的雙向鏈表正確連接。</font>

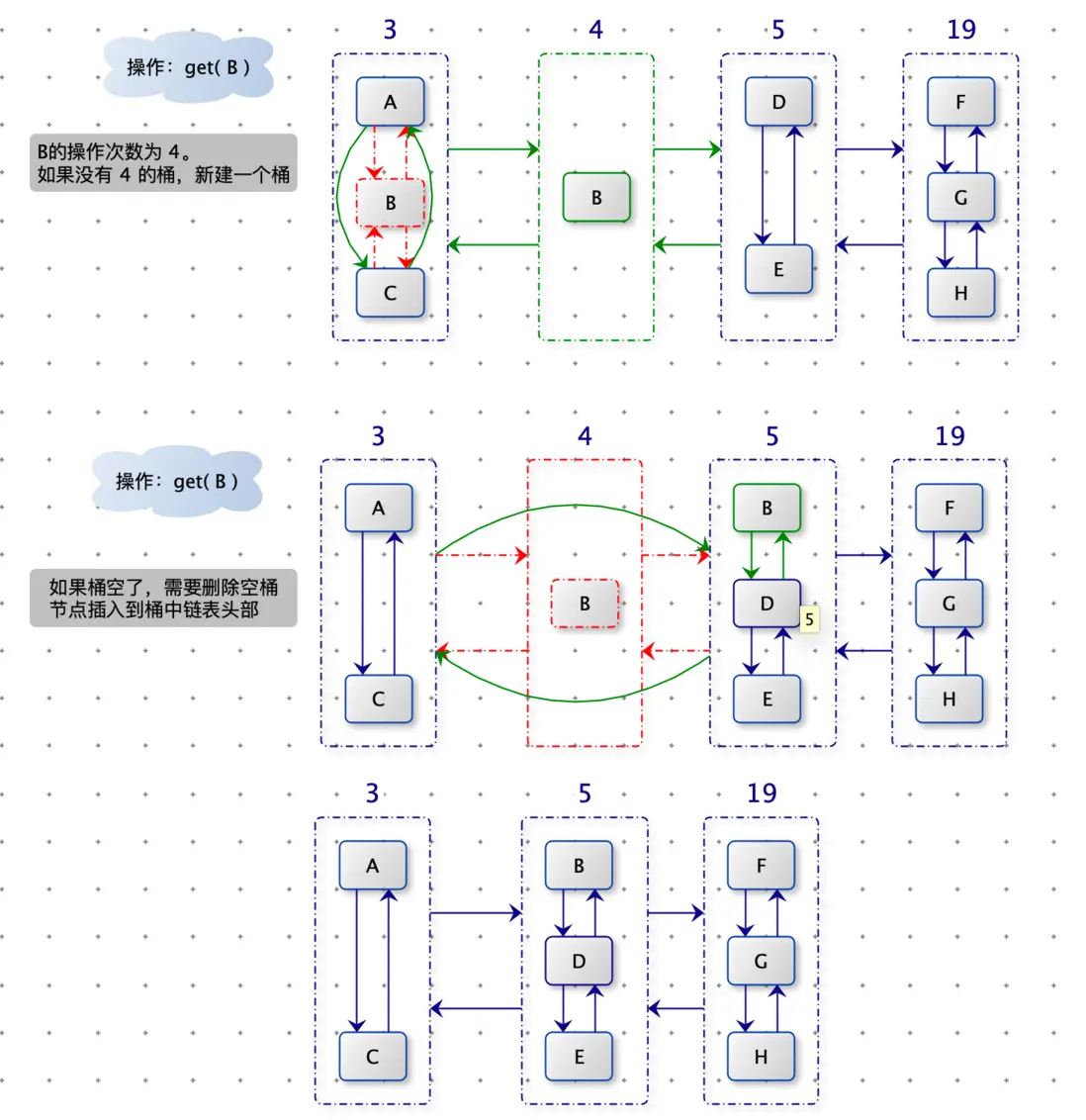
調用 get(B) ：B 的count 從 3 變為 4，沒有操作數為 4 的桶，就新建桶，將新桶插入在桶 3 和 桶 5 之間。將節點 B 從桶 3 中移除，插入桶 4 中。

再次調用 get(B)：B 的 count 從 4 變為 5，有操作數為 5 的桶，將節點 B 從桶 4 中移除，插入桶 5 （注意是頭節點）中。桶 4 移除節點 B 後，成為空桶，刪除空桶。將桶 3 與 桶 5 直接連接。

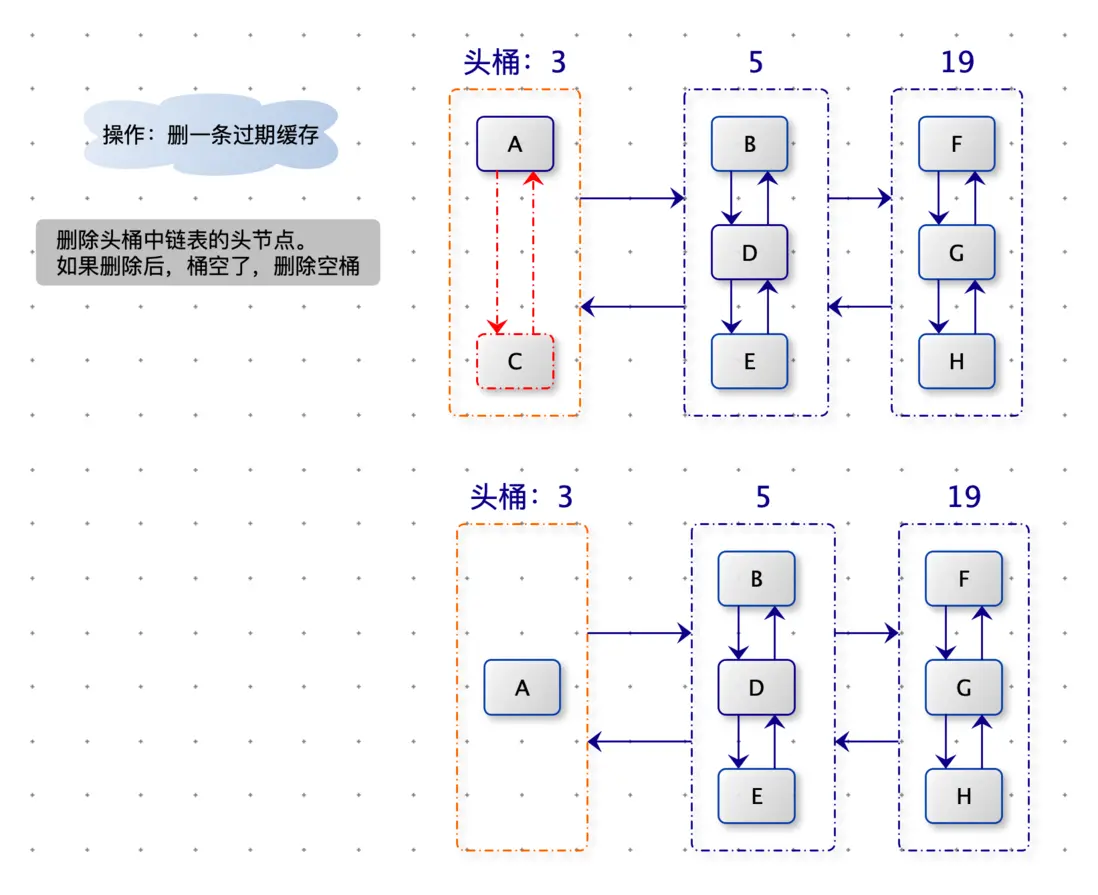
當需要刪除一條過期數據時，我們需要在頭桶中，刪除桶內鏈表的尾節點（尾結點是最早操作的數據）。

時間複雜度：O(1)

空間複雜度：O(K)

import java.util.*;

public class LFU2 {
    public static class Node {
        public int key;
        public int value;
        // 這個節點發生get或者set的次數總和
        public int count;
        // 雙向鏈表上一個節點
        public Node up;
        // 雙向鏈表下一個節點
        public Node down;

        public Node(int key, int value, int count) {
            this.key = key;
            this.value = value;
            this.count = count;
        }

        @Override
        public String toString() {
            return "Node{" + "key=" + key + ", value=" + value + ", count=" + count + '}';
        }
    }

    public static class NodeList {
        // 桶內鏈表的頭節點
        public Node head;
        // 桶內鏈表的尾節點
        public Node tail;
        // 桶之間的前一個桶
        public NodeList last;
        // 桶之間的後一個桶
        public NodeList next;


        public NodeList(Node node) {
            this.head = node;
            this.tail = node;
        }

        // 把一個新的節點加入這個桶，新的節點都放在頂端變成新的頭部
        public void addNodeFromHead(Node newHead) {
            newHead.down = head;
            head.up = newHead;
            head = newHead;
        }

        // 判斷這個桶是不是空的
        public boolean isEmpty() {
            return this.head == null;
        }

        // 刪除 node 節點並保證 node 的上下環境重新連接
        public void deleteNode(Node node) {
            if (head == tail) {
                this.head = null;
                this.tail = null;
            } else if (node == head) {
                head = node.down;
                head.up = null;
            } else if (node == tail) {
                tail = node.up;
                tail.down = null;
            } else {
                node.up.down = node.down;
                node.down.up = node.up;
            }
            node.up = null;
            node.down = null;
        }
    }


    // 總得緩存結構
    public static class LFUCache {
        // 緩存的大小限制
        public int capacity;
        // 緩存中目前有多少個節點
        public int size = 0;

        public Map<Integer, Node> map = new HashMap<>();
        // 表示節點 node在 哪個桶裏
        public Map<Node, NodeList> heads = new HashMap<>();
        // 整個桶鏈表的頭節點
        private NodeList headList;

        public LFUCache(int k) {
            this.capacity = k;
        }

        // removeNodeList：剛剛減少了一個節點的桶
        // 這個函數的功能是，判斷剛剛減少了一個節點的桶是不是已經空了。
        // 1）如果不空，什麼也不做
        // 2)如果空了，removeNodeList 還是整個緩存結構最左的桶 (headList)。
        // 刪掉這個桶的同時也要讓最左的桶變成removeNodeList的下一個。
        // 3)如果空了，removeNodeList不是整個緩存結構最左的桶(headList)。
        // 把這個桶刪除，並保證上一個的桶和下一個桶之間還是雙向鏈表的連接方式
        // 函數的返回值表示剛剛減少了一個節點的桶是不是已經空了，空了返回true；不空返回false
        private boolean modifyHeadList(NodeList removeNodeList) {
            if (!removeNodeList.isEmpty()) {
                return false;
            }
            if (removeNodeList == headList) {
                headList = removeNodeList.next;
                if (headList != null) {
                    headList.last = null;
                }
            } else {
                removeNodeList.last.next = removeNodeList.next;
                if (removeNodeList.next != null) {
                    removeNodeList.next.last = removeNodeList.last;
                }
            }
            return true;
        }

        // node 這個節點的次數 +1 了，這個節點原來在 oldNodeList 裏。
        // 把 node 從 oldNodeList 刪掉，然後放到次數 +1 的桶中
        // 整個過程既要保證桶之間仍然是雙向鏈表，也要保證節點之間仍然是雙向鏈表
        private void move(Node node, NodeList oldNodeList) {
            // 從 oldNodeList 中刪除
            oldNodeList.deleteNode(node);
            // preList表示次數 +1 的桶的前一個桶是誰
            // 如果 oldNodeList 刪掉 node 之後還有節點（oldNodeList 不需要刪除），oldNodeList 就是次數 +1 的桶的前一個桶
            // 如果 oldNodeList 刪掉 node 之後空了，oldNodeList是需要刪除的，所以次數 +1 的桶的前一個桶，是 oldNodeList 的前一個
            NodeList preList = modifyHeadList(oldNodeList) ? oldNodeList.last : oldNodeList;


            NodeList nextList = oldNodeList.next;
            // 如果 oldNodeList 沒有後續了，那麼肯定需要新建一個桶來盛放 node
            if (nextList == null) {
                NodeList newList = new NodeList(node);
                if (preList != null) {
                    preList.next = newList;
                }
                newList.last = preList;
                if (headList == null) {
                    headList = newList;
                }
                heads.put(node, newList);
            } else {
                // oldNodeList 有後續了，並且 oldNodeList 的後續count == node.count，直接將 node 添加到這個桶裏。
                if (nextList.head.count == node.count) {
                    nextList.addNodeFromHead(node);
                    heads.put(node, nextList);
                } else {
                    // oldNodeList 的後續 count != node.count ，那麼需要新建一個桶來放 node。
                    NodeList newList = new NodeList(node);
                    if (preList != null) {
                        preList.next = newList;
                    }
                    newList.last = preList;
                    newList.next = nextList;
                    nextList.last = newList;
                    if (headList == nextList) {
                        headList = newList;
                    }
                    heads.put(node, newList);
                }
            }
        }

        public void set(int key, int value) {
            // 更新
            if (map.containsKey(key)) {
                Node node = map.get(key);
                node.count++;
                node.value = value;
                move(node, heads.get(node));
            } else {
                // 新增
                // 如果緩存已滿，需要淘汰一條舊數據
                if (size == capacity) {
                    // 從頭部新增，從尾部刪除。桶內雙向鏈表的順序，就是相同 count 的 time 值的排序。
                    // headList 是 count 值最小的桶，headList.tail 是 time 最小的節點。
                    Node node = headList.tail;
                    headList.deleteNode(node);
                    // 刪除數據節點後，維護一下 桶，看看是否需要刪除
                    modifyHeadList(headList);

                    map.remove(node.key);
                    heads.remove(node);
                    size--;
                }

                Node node = new Node(key, value, 1);
                if (headList == null) {
                    headList = new NodeList(node);
                } else {
                    // 新增節點 count = 1，如果 headList 的count 也是 1，直接將 node 加入 headList
                    if (headList.head.count == node.count) {
                        headList.addNodeFromHead(node);
                    } else {
                        // 如果如果 headList 的count 不是 1，需要新建一個 count = 1 的桶，作為 headList
                        NodeList newList = new NodeList(node);
                        newList.next = headList;
                        headList.last = newList;
                        headList = newList;
                    }
                }
                size++;
                map.put(key, node);
                heads.put(node, headList);
            }
        }

        public Integer get(int key) {
            if (!map.containsKey(key)) {
                return null;
            }

            Node node = map.get(key);
            node.count++;
            move(node, heads.get(node));
            return node.value;
        }
    }
}

對數器

        public static boolean check(LFU1.LFUCache lfu1, LFU2.LFUCache lfu2, LFU3.LFUCache lfu3) {
            if (lfu1.map.size() != lfu2.heads.size() || lfu1.map.size() != lfu3.map.size()) {
                return false;
            }

            for (int key : lfu1.map.keySet()) {
                if (!lfu2.map.containsKey(key) || !lfu3.map.containsKey(key)) {
                    return false;
                }
                Node node = lfu1.map.get(key);
                LFU2.Node node2 = lfu2.map.get(key);
                LFU2.Node node3 = lfu2.map.get(key);

                if (node.value != node2.value || node.count != node2.count || node.value != node3.value || node.count != node3.count) {
                    return false;
                }
            }
            return true;

        }

        public static void check() {
            LFU1.LFUCache lfu1 = new LFU1.LFUCache(3);
            LFU2.LFUCache lfu2 = new LFU2.LFUCache(3);
            LFU3.LFUCache lfu3 = new LFU3.LFUCache(3);

            for (int i = 0; i < 100000; i++) {
                int command = (int) (Math.random() * 3) % 2;
                int key = (int) (Math.random() * 10);
                int value = (int) (Math.random() * 10);

                if (command == 0) {
                    lfu1.set(key, value);
                    lfu2.set(key, value);
                    lfu3.set(key, value);
                } else {
                    lfu1.get(key);
                    lfu2.get(key);
                    lfu3.get(key);
                }
                if (!check(lfu1, lfu2, lfu3)) {
                    System.out.println("ERROR:res1:" + key);
                }
            }

            System.out.println("Nice");
        }

        public static void main(String[] args) {
            check();
        }

本文由mdnice多平台發佈