漢諾塔：漢諾塔（又稱河內塔）問題是源於印度一個古老傳説的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞着64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。

漢諾塔問題分三步：

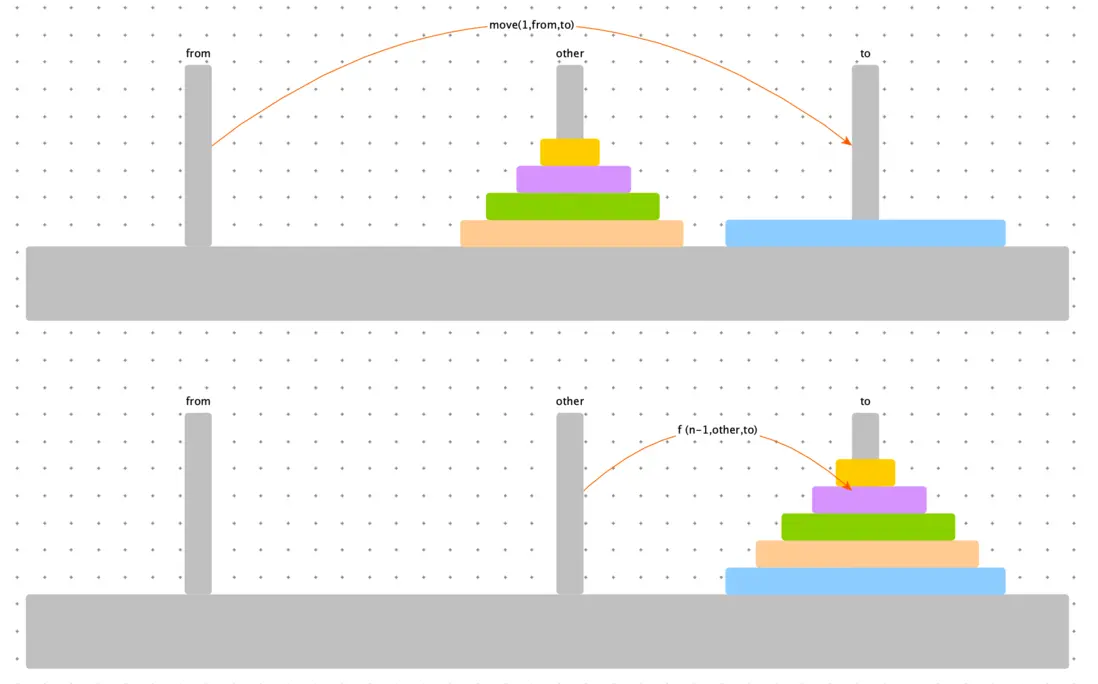
1. 將 0 ~ n -1 號圓盤從 from 柱子移動到 other 柱子。
2. 將 n 號圓盤從 from 柱子移動到 to 柱子。
3. 將 0 ~ n - 1 號圓盤從 other 柱子移動到 to 柱子。

def hanoi(n):
    if n <= 0: return
    func(n, "左", "右", "中")

def func(i, start, end, other):
    if i == 1:
        print("Move 1 from " + start + " to " + end)
        return
    func(i - 1, start, other, end)
    print("Move " + str(i) + " from" + start + " to " + end)
    func(i - 1, other, end, start)

hanoi(3)

漢諾塔遊戲的要求把所有的圓盤從左邊都移到右邊的柱子上，給定一個整型數組arr，其中只含有1、2、3，代表所有圓盤目前的狀態，1 代表左柱，2代表中柱，3 代表右柱，arr[i] 的值代表第 i + 1 個圓盤的位置。

比如：arr = [3,3,2,1] ，代表第 1 個圓盤在右柱上，第 2 個圓盤在右柱上，第 3 個圓盤在中柱上，第 4 個圓盤在左柱上。

如果 arr 代表的狀態是最優移動軌跡過程中出現的狀態，返回 arr 這種狀態是最優移動軌跡中第幾狀態；如果 arr 代表的狀態不是最優移動軌跡過程中出現的狀態，則返回 -1。

解法一：暴力遞歸

分析：

結論：n 層漢諾塔一共需要 $2^n-1$ 次移動圓盤。

漢諾塔問題分三步：

1. 將 0 ~ n -1 號圓盤從 from 柱子移動到 other 柱子，需要 $2^{n-1}-1$ 次移動圓盤。
2. 將 n 號圓盤從 from 柱子移動到 to 柱子，需要 1 次移動圓盤。
3. 將 0 ~ n - 1 號圓盤從 other 柱子移動到 to 柱子，需要 $2^{n-1}-1$ 次移動圓盤。

可能性分析：

• 假設 n 號圓盤在 from 柱子上，説明第一大步還沒走完，此時最優移動軌跡中的第幾狀態，取決於第一大步移動了多少次圓盤。
• 假設 n 號圓盤在 other 柱子上，從下圖可知 n 號圓盤不可能出現在 other 柱子上，説明次走法的不是最優移動軌跡，返回 -1。
• 假設 n 號圓盤在 to 柱子上，説明第一大步和第二大步已經走完，此時最優移動軌跡中的第幾狀態 = 第一大步所有的移動次數 + 第二大步所有的移動次數 + 第三大步真實移動次數 = $(2^{n-1}-1) + 1 + rest = 2{n-1}+rest$。

時間複雜度：O(N)

def step(arr):
    if not arr: return 0
    return f(arr, len(arr) - 1, 1, 2, 3)

# 目標：把 arr[0~i] 的圓盤，從 from 全部挪到 to 上
# 返回：根據 arr 中狀態 arr[0~i] ,它是最優解的第幾步？
# 時間複雜度：O(N)
def f(arr, i, fro, other, to):
    if i == -1: return 0
    if arr[i] != fro and arr[i] != to:
        return -1
    if arr[i] == fro:
        # 第一大步沒走完，arr[0~i-1] from --> other
        return f(arr, i - 1, fro, to, other)
    # 第三步完成的程度
    rest = f(arr, i - 1, other, fro, to)
    if rest == -1:
        return rest
    return (1 << i) + rest

解法二：非遞歸

def step1(arr):
    if not arr: return 0
    fro = 1
    other = 2
    to = 3
    i = len(arr) - 1
    res = 0
    while i >= 0:
        if arr[i] != fro and arr[i] != to: return -1
        if arr[i] == fro:
            res += 1 << i
            tmp = fro
            fro = other
        else:
            tmp = to
            to = other
        other = tmp
        i -= 1
    return res

對數器

import random

def check():
    for _ in range(1000):
        arr = [int(random.random() * 3) + 1 for _ in range(int(random.random() * 100))]
        res = step(arr)
        res1 = step(arr)
        if res != res1:
            print("ERROR","res=",res,"res1=",res1,arr)
    print("Nice")

check()