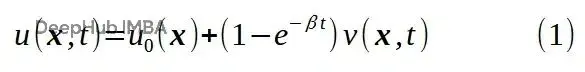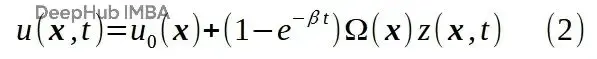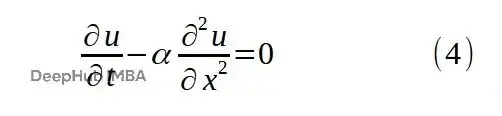PINNs出了名的難訓練。主要原因之一就是這個多目標優化問題。優化器很容易找到投機取巧的路徑——比如拼命降低微分方程殘差，但完全不管初始條件和邊界約束。只要給初始條件和邊界損失配的權重夠低，它們增加的那點損失完全能被殘差損失的大幅下降抵消掉。調整權重也許能暫時緩解這個問題，但誰也不能保證最優權重在整個訓練過程中一直有效。

標準的PINN用複合損失函數，把三項加權求和：

• 初始條件損失
• 邊界損失
• 微分方程殘差損失

要讓解有用，必須讓所有損失項同時降下來。用複合損失訓練PINN的時候，優化器面對多個目標，有什麼辦法讓優化器的工作簡單點呢？

硬約束

要簡化訓練，最好能把複合損失換成單一項。所以如果能設計一種神經網絡架構，讓它自動滿足初始和邊界條件那麼事情就會簡單很多了。初始條件和邊界條件直接"釘"在網絡結構裏，所以叫"硬約束"。相比之下，原始PINN把初始和邊界條件放在損失函數裏，那些約束是"軟"的——不保證精確滿足。

下面看看怎麼把這些約束具體嵌入網絡架構。

強制初始條件

初始條件一般是空間域上的一系列離散測量點。比如1D + t（一個空間維度加時間）的情況，初始條件就是沿x軸的一串值：(0 m, 100°C), (0.01 m, 105°C), (0.02 m, 106°C), … (0.3 m, 31°C)，諸如此類。

假設能用函數u₀(x)在整個空間域上插值。對1D + t的例子，如果_x_在樣本點上，u₀(_x_)返回觀測值；否則返回平滑插值，_x_ ∈ [0 m, 0.3 m]。三次樣條很適合幹這活。現在把初始條件的插值函數u₀(x)整合進PINN架構的輸出：

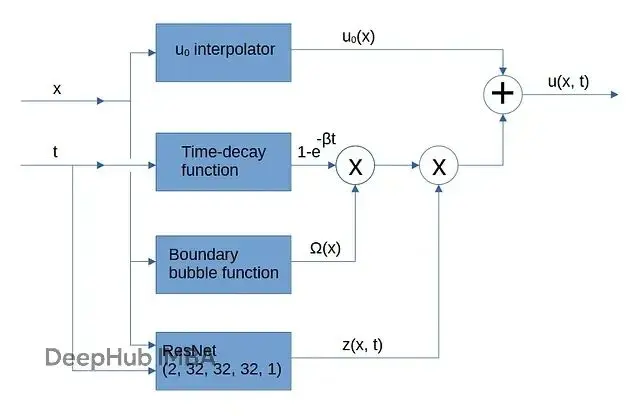
方程(1)給出了一種強制u(x, 0) = u₀(x)的方式。β是常數或者可訓練的時間衰減參數，決定了從初始狀態到熱擴散狀態的過渡期長短。任意函數v(x, t)是神經網絡的輸出，不過還有點額外的處理。

強制邊界條件

如果方程(1)裏的函數v(x, t)在邊界上取零值，再加上u₀(x)滿足Dirichlet邊界條件的假設，那麼u(xᵇ, t) = u₀(xᵇ)，這裏xᵇ是邊界上的點。

Ω(x)是個平滑函數，邊界處輸出零，空間域內部輸出非零有限值。可以想象成平面上的肥皂泡。

文獻[1]把Ω(_x_)叫做_approximate distance function_（近似距離函數），因為它的行為類似於輸出到最近邊界距離的函數。我覺得叫_boundary bubble function_（邊界泡泡函數）更形象點。

對1D + t情況，Ω(_x_)可以取拋物線形式，在空間邊界x_L和x_R處為零：

z(x, t)是任意函數的輸出。這裏用神經網絡。

輸出u(x, t)不是直接從可訓練網絡z(x, t)出來的，還能用梯度下降優化網絡參數嗎？

能。方程(3)裏涉及的其他函數（u₀(x)、時間衰減函數、邊界泡泡函數Ω(_x_)）對x和t都可導。深度學習框架反向傳播損失張量的時候會把它們的梯度算進去。所以初始條件插值、時間衰減、邊界泡泡函數的具體形式其實不太關鍵，神經網絡會自己適應。

用方程(3)作為PINN輸出的過濾器，就可以開始求解偏微分方程(PDE)了。

實驗

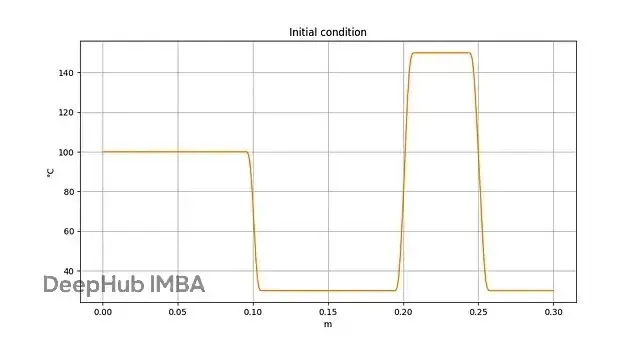
考慮一個薄金屬棒，初始温度分佈已知，來自一系列測量值。

初始條件，一系列温度測量點定義。圖片由作者提供。

描述温度隨時間演化的PDE是1D熱擴散方程：

這個問題的解析解是知道的，所以能拿PINN的結果跟解析解對比。

PINN架構核心是個三層ResNet，每層寬度32。

初始條件用三次樣條插值，邊界泡泡函數用拋物線：

class HardConstrained1dResNet(torch.nn.Module):
    def __init__(self, number_of_blocks, block_width, number_of_outputs,
                 initial_profile, time_bubble_beta=2.0):
        super().__init__()
        self.bubble = Bubble()
        self.z_predictor = pinn1d.ResidualNet(
            number_of_inputs=2,
            number_of_blocks=number_of_blocks,
            block_width=block_width,
            number_of_outputs=number_of_outputs
        )
        self.initial_profile = initial_profile
        delta_x = 1.0/(len(self.initial_profile) - 1)
        xs = np.arange(0, 1 + delta_x/2, delta_x)
        xy_list = []
        for x_ndx in range(len(xs)):
            x = xs[x_ndx]
            xy_list.append((x, self.initial_profile[x_ndx]))
        self.initial_profile_interpolator = interpolation1d.CubicSpline(
            xy_list, boundary_condition='2nd_derivative_0'
        )

        self.time_bubble_beta = torch.nn.Parameter(torch.tensor([time_bubble_beta]))

    def forward(self, x_t):  # x_t.shape = (B, 2)
        x_tsr = x_t[:, 0].unsqueeze(1)  # (B, 1)
        t_tsr = x_t[:, 1].unsqueeze(1)  # (B, 1)
        bubble_t_tsr = self.time_bubble(t_tsr)  # (B, 1)
        bubble_x_tsr = self.bubble(x_tsr)  # (B, 1)
        z_tsr = self.z_predictor(x_t)  # (B, 1)
        initial_interpolation_tsr = self.initial_profile_interpolator.batch_evaluate(x_tsr)
        return initial_interpolation_tsr + bubble_t_tsr * bubble_x_tsr * z_tsr

    def time_bubble(self, t_tsr):  # t_tsr.shape = (B, 1)
        return 1 - torch.exp(-self.time_bubble_beta * t_tsr)  # (B, 1)

訓練程序train.py裏，損失函數只有一項——微分方程殘差損失。初始條件和邊界損失架構設計就保證了，不用放到損失函數裏：

 (...)
  # Differential equation residual loss
  diff_eqn_residual_x_t_tsr.detach_()
  diff_eqn_residual_x_t_tsr.requires_grad = True
  du_dx__du_dt = first_derivative(neural_net, diff_eqn_residual_x_t_tsr)
  du_dt = du_dx__du_dt[:, 1]  # (N_res)

  d2u_dx2__d2u_dxdt = second_derivative(neural_net, diff_eqn_residual_x_t_tsr, 0)  # (N_res, 2)
  d2u_dx2 = d2u_dx2__d2u_dxdt[:, 0]  # (N_res)
  diff_eqn_residual = 1.0/duration * du_dt - alpha/length**2 * d2u_dx2  # (N_res)
  diff_eqn_residual_loss = criterion(diff_eqn_residual, torch.zeros_like(diff_eqn_residual))

  loss = diff_eqn_residual_loss
  is_champion = False
  (...)

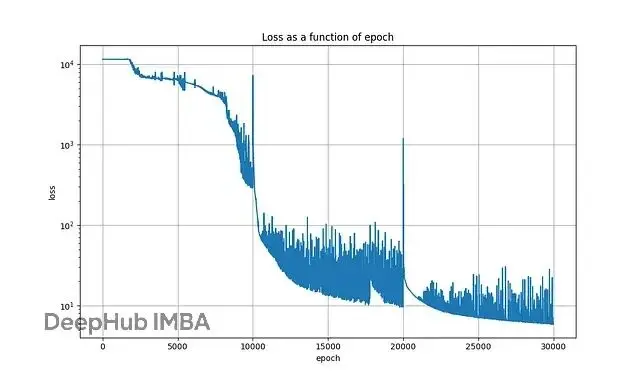
下圖是典型訓練過程的損失變化：

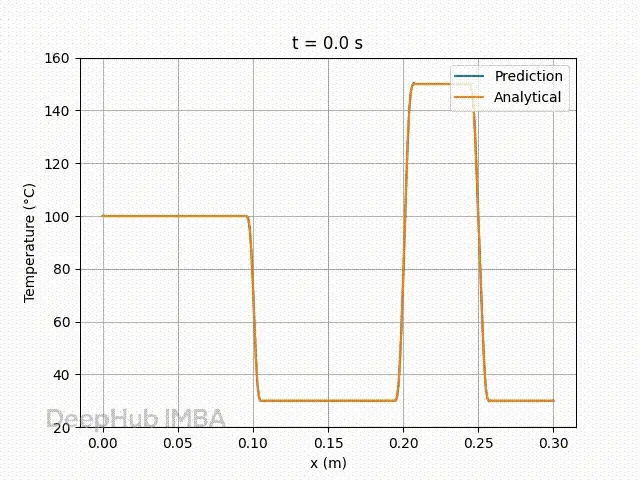
動畫1對比了10秒模擬期間的近似解和解析解：

PINN預測與解析解的比較。圖片由作者提供。

符合預期，t=0時的預測就是初始條件的插值，x=0 m和x=0.3 m處的温度值精確等於設定的邊界温度（Dirichlet邊界條件）。

總結

多目標優化給PINN訓練帶來的困難是實實在在的。設計上做點簡單修改，讓網絡輸出在t=0時自動匹配初始條件插值，在邊界上自動滿足邊界條件，就能把問題簡化不少。

訓練PINN解1D+t熱擴散問題的結果還不錯，從可視化能清楚看到PINN學會了滿足PDE，同時被強制滿足初始和邊界條件。

這套方法對那些物理約束不能妥協的領域可能挺有價值——氣候建模、生物醫學仿真之類的場景。

本文的代碼在這裏：

https://avoid.overfit.cn/post/4b21ca89cc714512bff16ffd1af69538
參考：

[1] Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks, N. Sukumar, Ankit Srivastava,

作者：Sébastien Gilbert