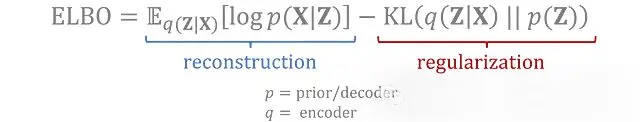變分自編碼器(VAEs)是一種生成式人工智能,因其能夠創建逼真的圖像而備受關注,它們不僅可以應用在圖像上,也可以創建時間序列數據。標準VAE可以被改編以捕捉時間序列數據的週期性和順序模式,然後用於生成合成數據。本文將使用一維卷積層、策略性的步幅選擇、靈活的時間維度和季節性依賴的先驗來模擬温度數據。
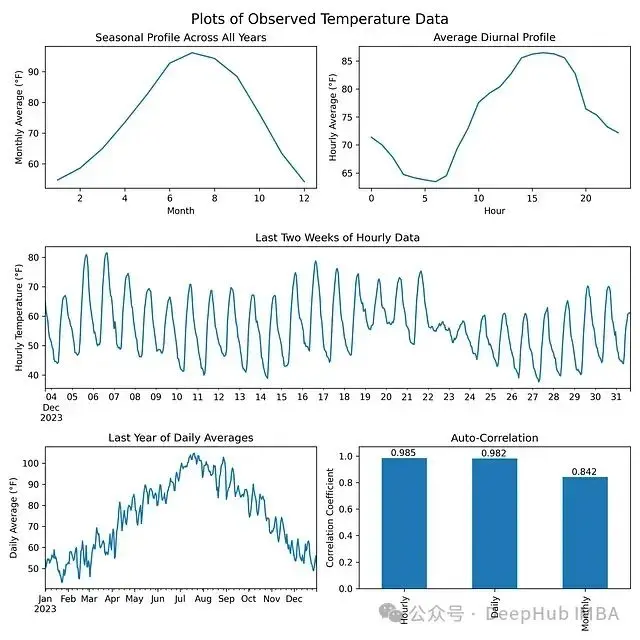
我們使用亞利桑那州菲尼克斯市50年的ERA5小時温度數據訓練了一個模型。為了生成有用的合成數據,它必須捕捉原始數據的幾個特徵:
- 季節性概況 — 夏季應該比冬季更暖
- 晝夜概況 — 白天應該比夜晚更暖
- 自相關性 — 數據應該平滑,連續幾天的温度應該相似
如果訓練數據是平穩的,沒有長期趨勢,模型表現最佳。但是由於氣候變化,温度呈現上升趨勢,每十年約上升0.7°F — 這個值來自觀測數據,與發表的顯示近期各地區變暖趨勢的地圖一致。為了考慮到温度上升,需要對原始觀測數據應用每十年-0.7°F的線性變換,消除上升趨勢。
什麼是VAE?
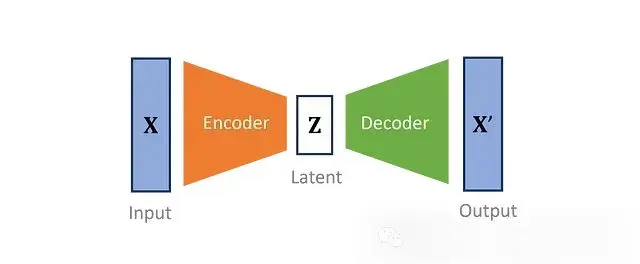
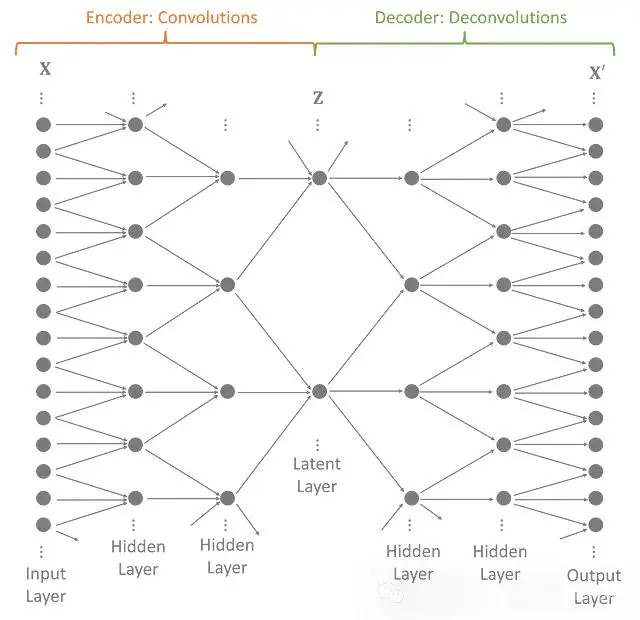
變分自編碼器將輸入數據的維度降低到一個更小的子空間。VAE定義了一個編碼器,將觀察到的輸入轉換成一種壓縮形式,稱為潛在變量。然後一個獨特的鏡像解碼器嘗試重建原始數據。編碼器和解碼器被共同優化,創建一個儘可能少損失信息的模型。
訓練中使用的完整損失函數包括:
- 重建損失: 測量經過往返轉換的數據與原始輸入的匹配程度
- 正則化項: 測量潛在變量的編碼分佈與先驗分佈的匹配程度
這兩個損失項是通過變分推斷得出的,目標是最大化觀測數據的證據下界(ELBO)。
VAE對訓練數據進行特徵提取,使得最重要的特徵(由潛在變量表示)遵循定義的先驗分佈。通過對潛在分佈進行採樣,然後將其解碼為原始輸入的形式,可以生成新的數據。
一維卷積層
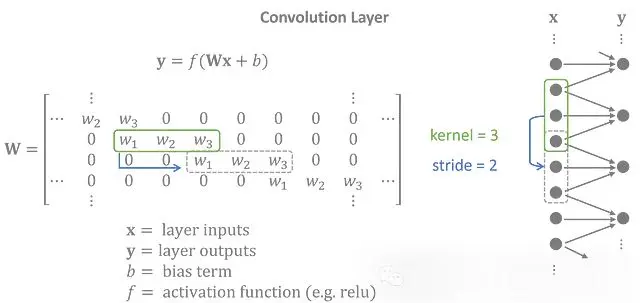
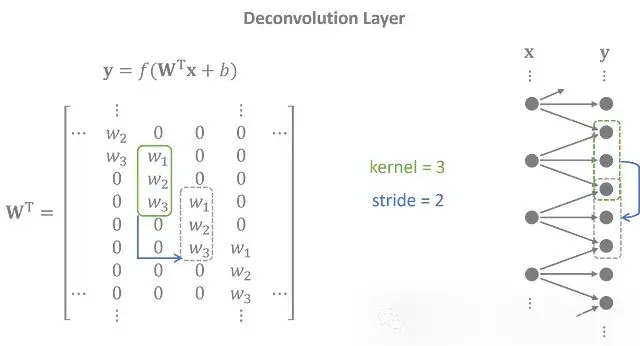
為了模擬温度數據,我們編碼器設計成一個具有一維卷積層的神經網絡。每個卷積層應用一個核 。由於在整個輸入中使用相同的核,卷積層被認為是平移不變的,非常適合具有重複序列模式的時間序列。
左: 作為矩陣運算的卷積層 | 右: 圖形表示
通常,輸入和輸出有幾個特徵變量。為簡單起見,矩陣運算顯示了僅有一個特徵的輸入和輸出之間的卷積。
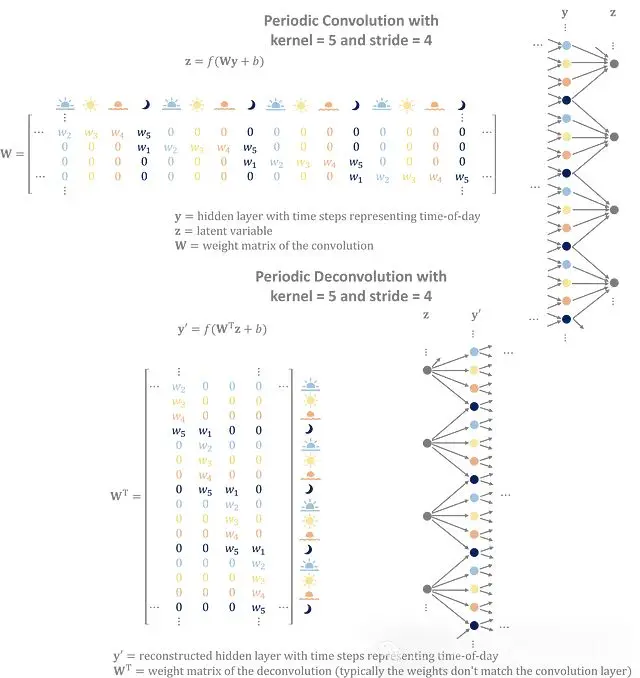
解碼器使用轉置的一維卷積層(也稱為反捲積層)執行與編碼器相反的任務。潛在特徵被投影到重疊的序列中,以創建一個與輸入緊密匹配的輸出時間序列。
反捲積層的權重矩陣是卷積矩陣的轉置。
完整的模型將幾個卷積層和反捲積層堆疊在一起。每個中間的隱藏層擴展潛在變量的範圍,使模型能夠捕捉數據中的長期效應。
步幅
步幅 — 移動之間的跳躍 — 決定了下一層的大小。卷積層使用步幅來縮小輸入,而反捲積層使用步幅將潛在變量擴展回輸入大小。它們還有一個次要目的 — 捕捉時間序列中的週期性趨勢。
你可以簡單的認為選擇卷積層的步幅是可以代表數據中的週期性模式。
將多個層堆疊在一起會產生一個由嵌套的子卷積組成的更大的有效週期。
考慮一個卷積網絡,它將每小時的時間序列數據提煉成每天四個變量,代表早晨、下午、傍晚和夜晚。一個步幅為4的層將有唯一分配給一天中每個時間的權重,在隱藏層中捕捉晝夜概況。在訓練過程中,編碼器和解碼器學習複製數據中發現的日循環的權重。
卷積利用輸入的週期性來構建更好的潛在特徵。反捲積將潛在特徵轉換為重疊的、重複的序列,以生成具有周期性模式的數據。
時間維度
生成圖像的VAE通常有數千張預處理成固定寬度和高度的圖像。生成的圖像將與訓練數據的寬度和高度相匹配。
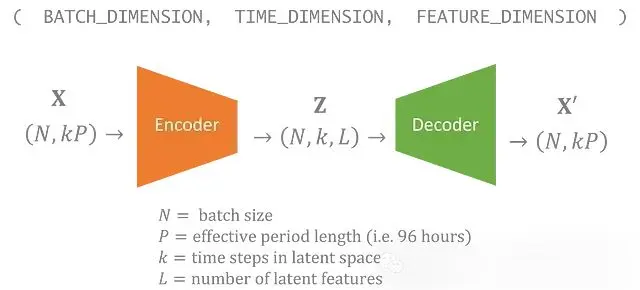
對於這個温度的數據集,我們有一個50年的時間序列。我麼可以為每96小時週期分配一個潛在變量。所以想要生成長於4天的時間序列,理想情況下,輸出應該是平滑的,而不是在模擬中有離散的96小時塊。
所以我門的潛在變量也包括一個可以變化的時間維度。在模型中,潛在空間中的每個時間步對應輸入中的96小時。
![]
生成新數據就像從先驗中採樣潛在變量一樣簡單,可以選擇想要包含在時間維度中的步數。
具有未受約束時間維度的VAE可以生成任意長度的數據。
季節性依賴的先驗
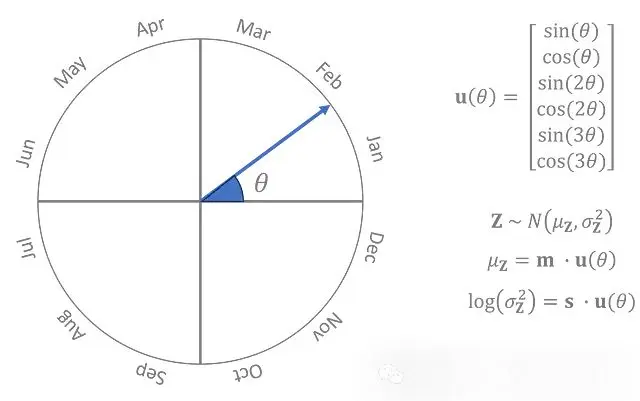
在大多數VAE中,潛在變量的每個分量被假定遵循標準正態分佈。這個分佈,有時被稱為先驗,被採樣然後解碼並且生成新的數據。在這種情況下,我們可以選擇一個稍微複雜一點的先驗,它依賴於一年中的時間。
從季節性先驗採樣的潛在變量將生成具有隨季節變化特徵的數據。
在這個先驗下,生成的一月數據將與七月數據看起來非常不同,而同一個月生成的數據將共享許多相同的特徵。
將一年中的時間表示為一個角度,θ,其中0°是1月1日,180°是7月初,360°又回到1月。先驗是一個正態分佈,其均值和對數方差是θ的三次三角多項式,其中多項式的係數是在訓練過程中與編碼器和解碼器一起學習的參數。
先驗分佈參數是θ的周期函數,而且良好行為的周期函數可以通過足夠高階的三角多項式以任何精度級別近似。
左: θ的可視化 | 右: Z的先驗分佈,用參數m和s表示
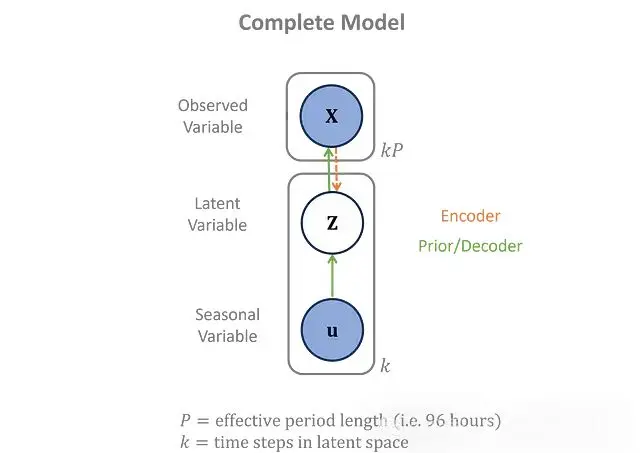
季節性數據僅用於先驗,不影響編碼器或解碼器。完整的概率依賴關係在這裏以圖形方式顯示。
上圖就是包括先驗的概率圖模型
代碼實現
為了簡化訓練步驟,我們使用Tensorflow開發這個模型
fromtensorflow.kerasimportlayers, models編碼器
輸入被定義為具有靈活的時間維度。在Keras中,你可以使用
None指定一個未受約束的維度。
使用
'same'填充將在輸入層附加零,使得輸出大小與輸入大小除以步幅相匹配。
inputs=layers.Input(shape=(None,)) # (N, 96*k)
x=layers.Reshape((-1, 1))(inputs) # (N, 96*k, 1)
# Conv1D parameters: filters, kernel_size, strides, padding
x=layers.Conv1D(40, 5, 3, 'same', activation='relu')(x) # (N, 32*k, 40)
x=layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 16*k, 40)
x=layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 8*k, 40)
x=layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 4*k, 40)
x=layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 2*k, 40)
x=layers.Conv1D(20, 3, 2, 'same')(x) # (N, k, 20)
z_mean=x[: ,:, :10] # (N, k, 10)
z_log_var=x[:, :, 10:] # (N, k, 10)
z=Sampling()([z_mean, z_log_var]) # custom layer sampling from gaussian
encoder=models.Model(inputs, [z_mean, z_log_var, z], name='encoder')Sampling()是一個自定義層,從給定均值和對數方差的正態分佈中採樣數據。
解碼器
反捲積是通過
Conv1DTranspose執行的。
# input shape: (batch_size, time_length/96, latent_features)
inputs=layers.Input(shape=(None, 10)) # (N, k, 10)
# Conv1DTranspose parameters: filters, kernel_size, strides, padding
x=layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(inputs) # (N, 2*k, 40)
x=layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 4*k, 40)
x=layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 8*k, 40)
x=layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 16*k, 40)
x=layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 32*k, 40)
x=layers.Conv1DTranspose(1, 5, 3, 'same')(x) # (N, 96*k, 1)
outputs=layers.Reshape((-1,))(x) # (N, 96*k)
decoder=models.Model(inputs, outputs, name='decoder')先驗
先驗期望輸入已經是[sin(θ), cos(θ), sin(2 θ), cos(2 θ), sin(3 θ), cos(3 θ)]的形式。
Dense層沒有偏置項,這是為了防止先驗分佈偏離零太遠或整體方差過高或過低。
# seasonal inputs shape: (N, k, 6)
inputs=layers.Input(shape=(None, 2*3))
x=layers.Dense(20, use_bias=False)(inputs) # (N, k, 20)
z_mean=x[:, :, :10] # (N, k, 10)
z_log_var=x[:, :, 10:] # (N, k, 10)
z=Sampling()([z_mean, z_log_var]) # (N, k, 10)
prior=models.Model(inputs, [z_mean, z_log_var, z], name='seasonal_prior')完整模型
損失函數包含一個重建項和一個潛在正則化項。
函數
log_lik_normal_sum是一個自定義函數,用於計算給定重建輸出的觀測數據的正態對數似然。計算對數似然需要解碼輸出周圍的噪聲分佈,這被假定為正態分佈,其對數方差由
self.noise_log_var給出,在訓練過程中學習。
對於正則化項,
kl_divergence_sum計算兩個高斯分佈之間的Kullback-Leibler散度 — 在這種情況下,是潛在編碼分佈和先驗分佈。
classVAE(models.Model):
def__init__(self, encoder, decoder, prior, **kwargs):
super(VAE, self).__init__(**kwargs)
self.encoder=encoder
self.decoder=decoder
self.prior=prior
self.noise_log_var=self.add_weight(name='var', shape=(1,), initializer='zeros', trainable=True)
@tf.function
defvae_loss(self, data):
values, seasonal=data
z_mean, z_log_var, z=self.encoder(values)
reconstructed=self.decoder(z)
reconstruction_loss=-log_lik_normal_sum(values, reconstructed, self.noise_log_var)/INPUT_SIZE
seasonal_z_mean, seasonal_z_log_var, _=self.prior(seasonal)
kl_loss_z=kl_divergence_sum(z_mean, z_log_var, seasonal_z_mean, seasonal_z_log_var)/INPUT_SIZE
returnreconstruction_loss, kl_loss_z
deftrain_step(self, data):
withtf.GradientTape() astape:
reconstruction_loss, kl_loss_z=self.vae_loss(data)
total_loss=reconstruction_loss+kl_loss_z
gradients=tape.gradient(total_loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
return {'loss': total_loss}結果
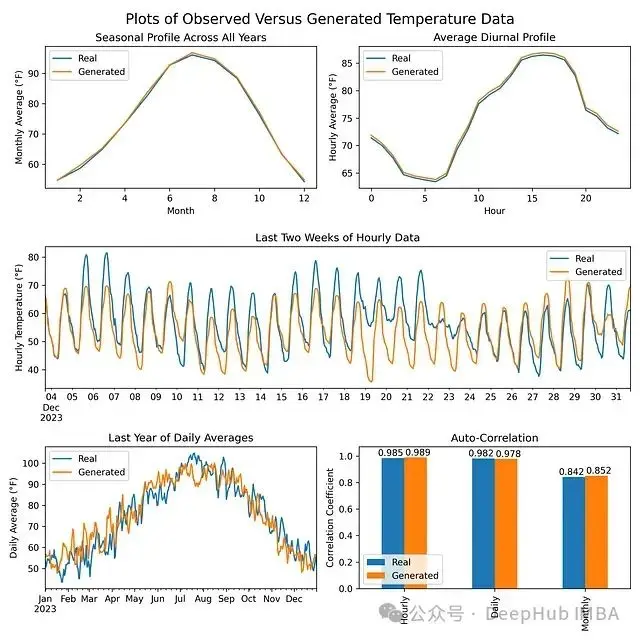
在訓練模型後,生成的數據與原始温度數據的季節性/晝夜概況和自相關性相匹配。
總結
構建生成式時間序列建模技術是一個關鍵領域,其應用遠不止於模擬數據。我們這個方法可以適用於數據插補、異常檢測和預測等應用。
通過使用一維卷積層、策略性步幅、靈活的時間輸入和季節性先驗,可以構建一個能夠複製時間序列中複雜模式的VAE。讓我們合作完善時間序列建模的最佳實踐。
本文代碼如下:
https://avoid.overfit.cn/post/d7b944fdc95144dc9d9ba694ed1f73fc
作者:David Kyle