做過電力負荷預測或者交通預測朋友，大概率都處理過時間特徵。這裏最直接的做法通常是把時間（比如分鐘或小時）直接扔進模型裏。這看起來邏輯自洽，但存在這一個大坑，就是“午夜悖論”。

比如説你的模型面對兩個時間點：23:59（一天的第1439分鐘） 和 00:01（一天的第1分鐘）。在我們的認知裏，這倆只差兩分鐘，但在模型的邏輯裏1439 和 1 可是不一樣的。大多數機器學習算法（線性迴歸、KNN、SVM 甚至神經網絡）在處理數值時，默認遵循線性邏輯：數值越大，代表的量級越高。它們理解不了“時間是循環的”這個概念。對它們來説午夜不是終點回到起點的閉環，而是一個斷崖。

這就是為什麼你加了時間特徵，模型卻在日期變更線附近表現拉胯的根本原因。

傳統編碼方式的侷限性

處理時間特徵，最常見的路數無非兩種，但這兩種都有硬傷。

整數編碼（Integer Encoding）

把 0 到 23 點編碼成數字 0-23。這就人為製造了一個斷層：23 到 0 的跳躍，被模型視作全天最大的波動。但實際上，晚上 11 點到午夜的變化，跟晚上 9 點到 10 點有什麼本質區別嗎？完全沒有。

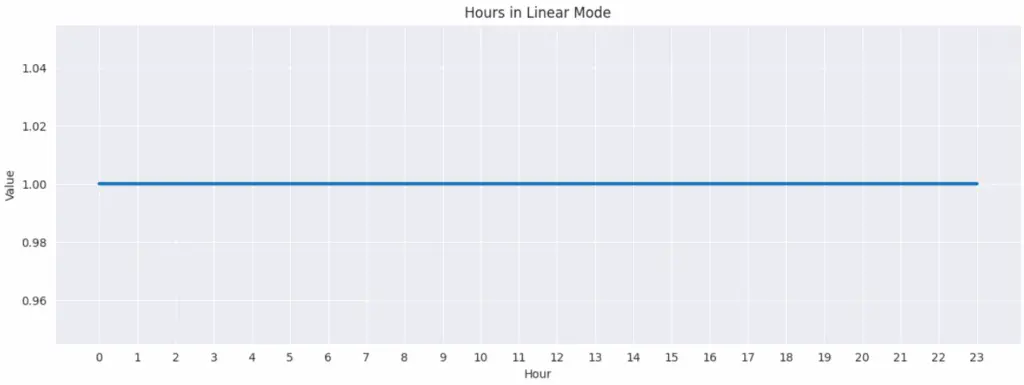
下面是這種線性模式下，時間特徵在數據層面的表現。

 # Generate data
date_today = pd.to_datetime('today').normalize()
datetime_24_hours = pd.date_range(start=date_today, periods=24, freq='h')
df = pd.DataFrame({'dt': datetime_24_hours})
df['hour'] = df['dt'].dt.hour

# Calculate Sin and Cosine
df["hour_sin"] = np.sin(2 * np.pi * df["hour"] / 24)
df["hour_cos"] = np.cos(2 * np.pi * df["hour"] / 24)

# Plot the Hours in Linear mode
plt.figure(figsize=(15, 5))
plt.plot(df['hour'], [1]*24, linewidth=3)
plt.title('Hours in Linear Mode')
plt.xlabel('Hour')
plt.xticks(np.arange(0, 24, 1))
plt.ylabel('Value')
 plt.show()

線性模式下的小時表示。

獨熱編碼（One-hot Encoding）

既然連續數字有問題，那拆成 24 個獨立的列呢？斷層是沒了但丟失了更重要的東西:鄰近性（Proximity）。在獨熱編碼下，凌晨 2 點和 3 點的距離，跟它和晚上 10 點的距離是一樣的。模型失去了“時間相鄰”這個上下文信息,更別提這會讓特徵維度爆炸，樹模型處理起來效率低，線性模型跑起來也費勁。

解決方案：三角函數映射（Trigonometric Mapping）

解決這個問題的核心在於思維視角的轉換：不要把時間看作一條直線，而要看作一個圓。

24小時是一個閉環,我們的編碼方式也得閉環。把每一個小時想象成圓周上均勻分佈的點,要確定圓上一個點的位置單靠一個數值是不夠的，我們需要兩個座標： x and y

這就是正弦（Sine）和餘弦（Cosine）發揮作用的地方。

幾何原理

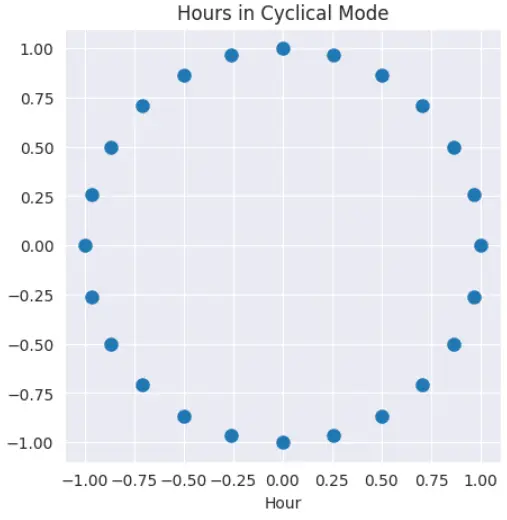
圓周上的任意角度都可以通過正弦和餘弦映射到一個唯一的座標點。這種映射賦予了模型一個平滑、連續的時間表示。

 plt.figure(figsize=(5, 5))
 plt.scatter(df['hour_sin'], df['hour_cos'], linewidth=3)
 plt.title('Hours in Cyclical Mode')
 plt.xlabel('Hour')
 

經過正弦和餘弦轉換後的循環模式。

計算公式非常簡單：

2 * π * hour / 24

：先把小時數值轉化成弧度角度。在這個體系下，午夜和晚上 11 點的角度非常接近，通過

sin

和

cos

將角度投影到兩個座標軸上。

這兩個值結合在一起唯一確定了當前的小時，23:00 和 00:00 在特徵空間裏的距離就被拉得很近了，這正是我們想要的效果。

這套邏輯同樣適用於分鐘、星期、月份等任何具有周期性的特徵。

代碼實戰

我們拿 UCI 的 Appliances Energy Prediction 數據集來跑個對比實驗。模型選用隨機森林迴歸器（Random Forest Regressor）。

Candanedo, L. (2017). Appliances Energy Prediction [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C5VC8G. Creative Commons 4.0 License.

 # Imports
 from sklearn.ensemble import RandomForestRegressor
 from sklearn.model_selection import train_test_split
 from sklearn.metrics import root_mean_squared_error
 from ucimlrepo import fetch_ucirepo 
 

獲取數據：

 # fetch dataset 
appliances_energy_prediction = fetch_ucirepo(id=374) 

# data (as pandas dataframes) 
X = appliances_energy_prediction.data.features 
y = appliances_energy_prediction.data.targets 

# To Pandas
df = pd.concat([X, y], axis=1)
df['date'] = df['date'].apply(lambda x: x[:10] + ' ' + x[11:])
df['date'] = pd.to_datetime(df['date'])
df['month'] = df['date'].dt.month
df['day'] = df['date'].dt.day
df['hour'] = df['date'].dt.hour
df.head(3)
 

先建立一個基準模型（Baseline），使用未處理的線性時間特徵。

 # X and y
# X = df.drop(['Appliances', 'rv1', 'rv2', 'date'], axis=1)
X = df[['hour', 'day', 'T1', 'RH_1', 'T_out', 'Press_mm_hg', 'RH_out', 'Windspeed', 'Visibility', 'Tdewpoint']]
y = df['Appliances']

# Train Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit the model
lr = RandomForestRegressor().fit(X_train, y_train)

# Score
print(f'Score: {lr.score(X_train, y_train)}')

# Test RMSE
y_pred = lr.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred)
print(f'RMSE: {rmse}')
 

基準結果如下：

 Score: 0.9395797670166536
 RMSE: 63.60964667197874
 

接下來我們對

hour

和

day

進行循環編碼，替換掉原來的線性特徵然後重新訓練模型。

 # Add cyclical hours sin and cosine
df['hour_sin'] = np.sin(2 * np.pi * df['hour'] / 24)
df['hour_cos'] = np.cos(2 * np.pi * df['hour'] / 24)
df['day_sin'] = np.sin(2 * np.pi * df['day'] / 31)
df['day_cos'] = np.cos(2 * np.pi * df['day'] / 31)

# X and y
X = df[['hour_sin', 'hour_cos', 'day_sin', 'day_cos','T1', 'RH_1', 'T_out', 'Press_mm_hg', 'RH_out', 'Windspeed', 'Visibility', 'Tdewpoint']]
y = df['Appliances']

# Train Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit the model
lr_cycle = RandomForestRegressor().fit(X_train, y_train)

# Score
print(f'Score: {lr_cycle.score(X_train, y_train)}')

# Test RMSE
y_pred = lr_cycle.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred)
print(f'RMSE: {rmse}')
 

結果顯示，Score 提升了約 1%，RMSE 下降了 1 個點。

 Score: 0.9416365489096074
 RMSE: 62.87008070927842
 

看着提升不大？這只是一個簡單的 Toy Example，也沒做任何精細的數據清洗。但這裏的提升完全來自於正弦和餘弦變換帶來的特徵表達能力的增強。

本質上這讓模型“看懂”了現實世界中電力需求的連續性,它並不會因為時鐘跳過 0 點就突然歸零。

為什麼 Sin 和 Cos 缺一不可？

很多人可能會想，只用 Sin 這一列行不行？還能省點特徵維度。答案是不行。這會破壞對稱性。在一個 24 小時的圓周上，早上 6 點和晚上 6 點的 Sine 值可能是一樣的。如果只給模型一個值，它就會混淆這兩個截然不同的時間段（比如早高峯和晚高峯）。必須同時使用 Sin 和 Cos就像定位必須要有經度和緯度一樣。只有這樣圓上的每一個小時才能擁有唯一的“特徵指紋”。

實際應用中的收益

這套方法在不同模型下的收益是不一樣的：

• 基於距離的模型（KNN, SVMs）：這是最大的受益者。循環編碼消除了邊界上的偽“長距離”，讓數據點之間的距離計算迴歸真實。
• 神經網絡（Neural Networks）：平滑的特徵空間有助於網絡更快的收斂和更穩定的訓練表現，消除了午夜那種劇烈的數值跳變。
• 樹模型（Tree-based models）：雖然像 XGBoost 或 LightGBM 這種強力模型最終也能通過不斷分裂學到這種模式，但提供循環編碼特徵相當於給了它們一個極佳的先驗知識（Inductive Bias），在追求極致性能和解釋性時非常有用。

適用場景

使用這套方法的判斷標準很簡單，問自己一個問題：這個特徵是循環往復的嗎？如果是，那就試試。常見的例子包括：

• 一天中的小時（0-23）
• 一週中的星期（1-7）
• 一年中的月份（1-12）
• 風向（0-360度）

總結

時間在數據科學裏不應該只是一個冰冷的數字，它本質上是圓周上的座標。如果你執意把它當直線處理，模型在週期邊界處跌倒是遲早的事。使用正弦和餘弦進行循環編碼，是一種優雅且低成本的修正手段。它保留了數據的鄰近性，消除了人工偽影，能讓模型學得更快、更準。下次如果你的模型預測曲線在日期交界處出現詭異的跳變，不妨試試這個方法。

https://avoid.overfit.cn/post/5fea3ffcb7ac4b27a3a0d7bb55b9bd39

作者：Gustavo Santos