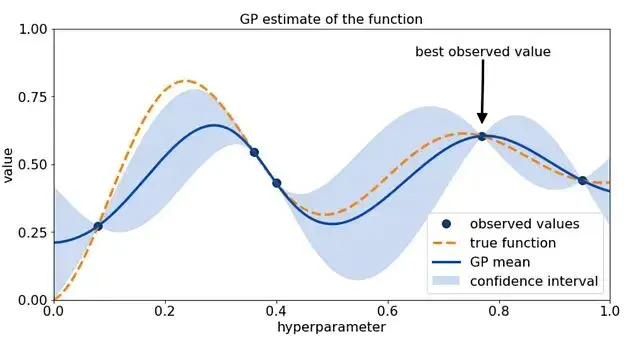
貝葉斯優化(Bayesian Optimization, BO)雖然是超參數調優的利器,但在實際落地中往往會出現收斂慢、計算開銷大等問題。很多時候直接“裸跑”標準庫裏的 BO,效果甚至不如多跑幾次 Random Search。
所以要想真正發揮 BO 的威力,必須在搜索策略、先驗知識注入以及計算成本控制上做文章。本文整理了十個經過實戰驗證的技巧,能幫助優化器搜索得更“聰明”,收斂更快,顯著提升模型迭代效率。
1、像貝葉斯專家一樣引入先驗(Priors)
千萬別冷啓動,優化器如果在沒有任何線索的情況下開始,為了探索邊界會浪費大量算力。既然我們通常對超參數範圍有一定領域知識,或者手頭有類似的過往實驗數據,就應該利用起來。
弱先驗會導致優化器在搜索空間中漫無目的地遊蕩,而強先驗能迅速坍縮搜索空間。在昂貴的 ML 訓練循環中,先驗質量直接決定了你能省下多少 GPU 時間。
所以可以先跑一個微型的網格搜索或隨機搜索(比如 5-10 次試驗),把表現最好的幾個點作為先驗,去初始化高斯過程(Gaussian Process)。
利用知情先驗初始化高斯過程
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import Matern
from skopt import Optimizer
# Step 1: Quick cheap search to build priors
def objective(params):
lr, depth = params
return train_model(lr, depth) # your training loop returning validation loss
search_space = [
(1e-4, 1e-1), # learning rate
(2, 10) # depth
]
# quick 8-run grid/random search
initial_points = [
(1e-4, 4), (1e-3, 4), (1e-2, 4),
(1e-4, 8), (1e-3, 8), (1e-2, 8),
(5e-3, 6), (8e-3, 10)
]
initial_results = [objective(p) for p in initial_points]
# Step 2: Build priors for Bayesian Optimization
kernel = Matern(nu=2.5)
gp = GaussianProcessRegressor(kernel=kernel, normalize_y=True)
# Step 3: Initialize optimizer with priors
opt = Optimizer(
dimensions=search_space,
base_estimator=gp,
initial_point_generator="sobol",
)
# Feed prior observations
for p, r in zip(initial_points, initial_results):
opt.tell(p, r)
# Step 4: Bayesian Optimization with informed priors
for _ in range(30):
next_params = opt.ask()
score = objective(next_params)
opt.tell(next_params, score)
best_params = opt.get_result().x
print("Best Params:", best_params)有 Kaggle Grandmaster 曾通過複用相似問題的先驗配置,減少了 40% 的調優輪次。用幾次廉價的評估換取貝葉斯搜索的加速,這筆交易很划算。
2、動態調整採集函數(Acquisition Function)
Expected Improvement (EI) 是最常用的採集函數,因為它在“探索”和“利用”之間取得了不錯的平衡。但在搜索後期,EI 往往變得過於保守,導致收斂停滯。
搜索策略不應該是一成不變的。當發現搜索陷入平原區時,可以嘗試動態切換採集函數:在需要激進逼近最優解時切換到 UCB(Upper Confidence Bound);在搜索初期或者目標函數噪聲較大需要跳出局部優時,切換到 PI(Probability of Improvement)。
動態調整策略能有效打破後期平台期,減少那些對模型提升毫無幫助的“垃圾時間”。這裏用
scikit-optimize演示如何根據收斂情況動態切換策略:
import numpy as np
from skopt import Optimizer
from skopt.acquisition import gaussian_ei, gaussian_pi, gaussian_ucb
# Dummy expensive objective
def objective(params):
lr, depth = params
return train_model(lr, depth) # Replace with your actual training loop
space = [(1e-4, 1e-1), (2, 10)]
opt = Optimizer(
dimensions=space,
base_estimator="GP",
acq_func="EI" # initial acquisition function
)
def should_switch(iteration, recent_scores):
# Simple heuristic: if scores haven't improved in last 5 steps, switch mode
if iteration > 10 and np.std(recent_scores[-5:]) < 1e-4:
return True
return False
scores = []
for i in range(40):
# Dynamically pick acquisition function
if should_switch(i, scores):
# Choose UCB when nearing convergence, PI for risky exploration
opt.acq_func = "UCB" if scores[-1] < np.median(scores) else "PI"
x = opt.ask()
y = objective(x)
scores.append(y)
opt.tell(x, y)
best_params = opt.get_result().x
print("Best Params:", best_params)3、善用對數變換(Log Transforms)
很多超參數(如學習率、正則化強度、Batch Size)在數值上跨越了幾個數量級,呈現指數分佈。這種分佈對高斯過程(GP)非常不友好,因為 GP 假設空間是平滑均勻的。
直接在原始空間搜索,優化器會把大量時間浪費在擬合那些陡峭的“懸崖”上。對這些參數進行對數變換(Log Transform),把指數空間拉伸成線性的,讓優化器在一個“平坦”的操場上跑。這不僅能穩定 GP 的核函數,還能大幅降低曲率,在實際調參中通常能把收斂時間減半。
import numpy as np
from skopt import Optimizer
from skopt.space import Real
# Expensive training function
def objective(params):
log_lr, log_reg = params
lr = 10 ** log_lr # inverse log transform
reg = 10 ** log_reg
return train_model(lr, reg) # replace with your actual training loop
# Step 1: Define search space in log10 scale
space = [
Real(-5, -1, name="log_lr"), # lr in [1e-5, 1e-1]
Real(-6, -2, name="log_reg") # reg in [1e-6, 1e-2]
]
# Step 2: Create optimizer with log-transformed space
opt = Optimizer(
dimensions=space,
base_estimator="GP",
acq_func="EI"
)
# Step 3: Run Bayesian Optimization entirely in log-space
n_iters = 40
scores = []
for _ in range(n_iters):
x = opt.ask() # propose in log-space
y = objective(x) # evaluate in real-space
opt.tell(x, y)
scores.append(y)
best_log_params = opt.get_result().x
best_params = {
"lr": 10 ** best_log_params[0],
"reg": 10 ** best_log_params[1]
}
print("Best Params:", best_params)4、別讓 BO 陷入“套娃”陷阱(Hyper-hypers)
貝葉斯優化本身也是有超參數的:Kernel Length Scales、噪聲項、先驗方差等。如果你試圖去優化這些參數,就會陷入“為了調參而調參”的無限遞歸。
BO 內部的超參數優化非常敏感,容易導致代理模型過擬合或者噪聲估計錯誤。對於工業級應用,更穩健的做法是早停(Early Stopping)GP 的內部優化器,或者直接使用元學習(Meta-Learning)得出的經驗值來初始化這些超-超參數。這能讓代理模型更穩定,更新成本更低,AutoML 系統通常都採用這種策略而非從零學起。
import numpy as np
from skopt import Optimizer
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import Matern, WhiteKernel
# Meta-learned priors from previous similar tasks
meta_length_scale = 0.3
meta_noise_level = 1e-3
kernel = (
Matern(length_scale=meta_length_scale, nu=2.5) +
WhiteKernel(noise_level=meta_noise_level)
)
# Early-stop BO's own hyperparameter tuning
gp = GaussianProcessRegressor(
kernel=kernel,
optimizer="fmin_l_bfgs_b",
n_restarts_optimizer=0, # Crucial: prevent expensive hyper-hyper loops
normalize_y=True
)
# BO with a stable, meta-initialized GP
opt = Optimizer(
dimensions=[(1e-4, 1e-1), (2, 12)],
base_estimator=gp,
acq_func="EI"
)
def objective(params):
lr, depth = params
return train_model(lr, depth) # your model's validation loss
scores = []
for _ in range(40):
x = opt.ask()
y = objective(x)
opt.tell(x, y)
scores.append(y)
best_params = opt.get_result().x
print("Best Params:", best_params)5、懲罰高成本區域
標準的 BO 只在乎準確率,不在乎你的電費單。有些參數組合(比如超大 Batch Size、極深的網絡、巨大的 Embedding 維度)可能只會帶來微小的性能提升,但計算成本卻是指數級增長的。
如果不管控成本,BO 很容易鑽進“高分低能”的牛角尖。所以可以修改採集函數,引入成本懲罰項。我們不看絕對性能,而是看單位成本的性能收益。斯坦福 ML 實驗室曾指出,忽略成本感知會導致預算超支 37% 以上。
成本感知的採集函數(Cost-Aware EI)
import numpy as np
from skopt import Optimizer
from skopt.acquisition import gaussian_ei
# Objective returns BOTH validation loss and estimated training cost
def objective(params):
lr, depth = params
val_loss = train_model(lr, depth)
cost = estimate_cost(lr, depth) # e.g., GPU hours or FLOPs proxy
return val_loss, cost
# Custom cost-aware EI: maximize EI / Cost
def cost_aware_ei(model, X, y_min, costs):
raw_ei = gaussian_ei(X, model, y_min=y_min)
normalized_costs = costs / np.max(costs)
penalty = 1.0 / (1e-6 + normalized_costs)
return raw_ei * penalty
# Search space
opt = Optimizer(
dimensions=[(1e-4, 1e-1), (2, 20)],
base_estimator="GP"
)
observed_losses = []
observed_costs = []
for _ in range(40):
# Ask a batch of candidate points
candidates = opt.ask(n_points=20)
# Evaluate cost-aware EI for each candidate
y_min = np.min(observed_losses) if observed_losses else np.inf
cost_scores = cost_aware_ei(
opt.base_estimator_,
np.array(candidates),
y_min=y_min,
costs=np.array(observed_costs[-len(candidates):] + [1]*len(candidates)) # fallback cost=1
)
# Pick best candidate under cost-awareness
next_x = candidates[np.argmax(cost_scores)]
(loss, cost) = objective(next_x)
observed_losses.append(loss)
observed_costs.append(cost)
opt.tell(next_x, loss)
best_params = opt.get_result().x
print("Best Params (Cost-Aware):", best_params)6、混合策略:BO + 隨機搜索
在噪聲較大的任務(如 RL 或深度學習訓練)中,BO 並非無懈可擊。GP 代理模型有時候會被噪聲“騙”了,導致對錯誤的區域過度自信,陷入局部最優。
這時候引入一點“混亂”反而有奇效。在 BO 循環中混入約 10% 的隨機搜索,能有效打破代理模型的“執念”,增加全局覆蓋率。這是一種用隨機性的多樣性來彌補 BO 確定性缺陷的混合策略,也是很多大規模 AutoML 系統的默認配置。
隨機-BO 混合模式
import numpy as np
from skopt import Optimizer
from skopt.space import Real, Integer
# Define search space
space = [
Real(1e-4, 1e-1, name="lr"),
Integer(2, 12, name="depth")
]
# Expensive training loop
def objective(params):
lr, depth = params
return train_model(lr, depth) # your model's validation loss
# BO Optimizer
opt = Optimizer(
dimensions=space,
base_estimator="GP",
acq_func="EI"
)
n_total = 50
n_random = int(0.20 * n_total) # first 20% = random exploration
results = []
for i in range(n_total):
if i < n_random:
# ----- Phase 1: Pure Random Search -----
x = [
np.random.uniform(1e-4, 1e-1),
np.random.randint(2, 13)
]
else:
# ----- Phase 2: Bayesian Optimization -----
x = opt.ask()
y = objective(x)
results.append((x, y))
# Only tell BO after evaluations (keeps history consistent)
opt.tell(x, y)
best_params = opt.get_result().x
print("Best Params (Hybrid):", best_params)7、並行化:偽裝成並行計算
BO 本質上是串行的(Sequential),因為每一步都依賴上一步更新的後驗分佈。這在多 GPU 環境下很吃虧。不過我們可以“偽造”並行性。
啓動多個獨立的 BO 實例,給它們設置不同的隨機種子或先驗。讓它們獨立跑,然後把結果彙總到一個主 GP 模型裏進行 Retrain。這樣既利用了並行計算資源,又通過多樣化的探索增強了最終代理模型的適應性。這種方法在 NAS(神經網絡架構搜索)中非常普遍。
多路並行 BO + 結果合併
import numpy as np
from skopt import Optimizer
from multiprocessing import Pool
# Search space
space = [(1e-4, 1e-1), (2, 10)]
# Expensive objective
def objective(params):
lr, depth = params
return train_model(lr, depth)
# Create BO instances with different priors/kernels
def make_optimizer(seed):
return Optimizer(
dimensions=space,
base_estimator="GP",
acq_func="EI",
random_state=seed
)
optimizers = [make_optimizer(seed) for seed in [0, 1, 2, 3]] # 4 BO tracks
# Evaluate one BO step for a single optimizer
def bo_step(opt):
x = opt.ask()
y = objective(x)
opt.tell(x, y)
return (x, y)
# Run pseudo-parallel BO for N steps
def run_parallel_steps(optimizers, steps=10):
pool = Pool(len(optimizers))
results = []
for _ in range(steps):
async_calls = [pool.apply_async(bo_step, (opt,)) for opt in optimizers]
for res, opt in zip(async_calls, optimizers):
x, y = res.get()
results.append((x, y))
pool.close()
pool.join()
return results
# Step 1: parallel exploration
parallel_results = run_parallel_steps(optimizers, steps=15)
# Step 2: merge results into a master BO
master = make_optimizer(seed=99)
for x, y in parallel_results:
master.tell(x, y)
# Step 3: refine with unified BO
for _ in range(30):
x = master.ask()
y = objective(x)
master.tell(x, y)
print("Best Params:", master.get_result().x)8、非數值輸入的處理技巧
高斯過程喜歡連續平滑的空間,但現實中的超參數往往包含非數值型變量(如優化器類型:Adam vs SGD,激活函數類型等)。這些離散的“跳躍”會破壞 GP 的核函數假設。
直接把它們當類別 ID 輸入給 GP 是錯誤的。正確的做法是使用 One-Hot 編碼 或者 Embedding。將類別變量映射到連續的數值空間,讓 BO 能理解類別之間的“距離”,從而恢復搜索空間的平滑性。在一個 BERT 微調的案例中,僅僅通過正確編碼
adam_vs_sgd,就帶來了 15% 的性能提升。
處理類別型超參數
import numpy as np
from skopt import Optimizer
from sklearn.preprocessing import OneHotEncoder
# --- Step 1: Prepare categorical encoder ---
optimizers = np.array([["adam"], ["sgd"], ["adamw"]])
enc = OneHotEncoder(sparse_output=False).fit(optimizers)
def encode_category(cat_name):
return enc.transform([[cat_name]])[0] # returns continuous 3-dim vector
# --- Step 2: Combined numeric + categorical search space ---
# Continuous params: lr, dropout
# Encoded categorical: optimizer
space_dims = [
(1e-5, 1e-2), # learning rate
(0.0, 0.5), # dropout
(0.0, 1.0), # optimizer_onehot_dim1
(0.0, 1.0), # optimizer_onehot_dim2
(0.0, 1.0) # optimizer_onehot_dim3
]
opt = Optimizer(
dimensions=space_dims,
base_estimator="GP",
acq_func="EI"
)
# --- Step 3: Objective that decodes embedding back to category ---
def decode_optimizer(vec):
idx = np.argmax(vec)
return ["adam", "sgd", "adamw"][idx]
def objective(params):
lr, dropout, *opt_vec = params
opt_name = decode_optimizer(opt_vec)
return train_model(lr, dropout, optimizer=opt_name)
# --- Step 4: Hybrid categorical-continuous BO loop ---
for _ in range(40):
x = opt.ask()
# Snap encoded optimizer vector to nearest valid one-hot
opt_vec = np.array(x[2:])
snapped_vec = np.zeros_like(opt_vec)
snapped_vec[np.argmax(opt_vec)] = 1.0
clean_x = [x[0], x[1], *snapped_vec]
y = objective(clean_x)
opt.tell(clean_x, y)
best_params = opt.get_result().x
print("Best Params:", best_params)9、約束不可探索區域
很多超參數組合理論上存在,但工程上跑不通。比如
batch_size大於數據集大小,或者
num_layers < num_heads等邏輯矛盾。如果不對其進行約束,BO 會浪費大量時間去嘗試這些必然報錯或無效的組合。
通過顯式地定義約束條件,或者在目標函數中對無效區域返回一個巨大的 Loss,可以迫使 BO 避開這些“雷區”。這能顯著減少失敗的試驗次數,通常能節省 25-40% 的搜索時間。
約束感知的貝葉斯優化
from skopt import gp_minimize
from skopt.space import Integer, Real, Categorical
import numpy as np
# Hyperparameter search space
space = [
Integer(8, 512, name="batch_size"),
Integer(1, 12, name="num_layers"),
Integer(1, 12, name="num_heads"),
Real(1e-5, 1e-2, name="learning_rate", prior="log-uniform"),
]
# Define constraints
def valid_config(params):
batch_size, num_layers, num_heads, _ = params
return (batch_size <= 12800) and (num_layers >= num_heads)
# Wrapped objective that enforces constraints
def objective(params):
if not valid_config(params):
# Penalize invalid regions so BO learns to avoid them
return 10.0 # large synthetic loss
# Fake expensive training loop
batch_size, num_layers, num_heads, lr = params
loss = (
(num_layers - num_heads) * 0.1
+ np.log(batch_size) * 0.05
+ np.random.normal(0, 0.01)
+ lr * 5
)
return loss
# Run constraint-aware BO
result = gp_minimize(
func=objective,
dimensions=space,
n_calls=40,
n_initial_points=8,
noise=1e-5
)
print("Best hyperparameters:", result.x)10、集成代理模型(Ensemble Surrogate Models)
單一的高斯過程模型並不總是可靠的。面對高維空間或稀疏數據,GP 容易產生“幻覺”,給出錯誤的置信度估計。
更穩健的做法是集成多個代理模型。我們可以同時維護 GP、隨機森林(Random Forest)和梯度提升樹(GBDT),甚至簡單的 MLP。通過投票或加權平均來決定下一步的搜索方向。這利用了集成學習的優勢,顯著降低了預測方差。在 Optuna 等成熟框架中,這種思想被廣泛應用。
import optuna
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
import numpy as np
# Build surrogate ensemble
def build_surrogates():
return [
GaussianProcessRegressor(normalize_y=True),
RandomForestRegressor(n_estimators=200),
GradientBoostingRegressor()
]
# Train all surrogates on past trials
def train_surrogates(surrogates, X, y):
for s in surrogates:
s.fit(X, y)
# Aggregate predictions using uncertainty-aware weighting
def ensemble_predict(surrogates, X):
preds = []
for s in surrogates:
p = s.predict(X, return_std=False)
preds.append(p)
return np.mean(preds, axis=0)
def objective(trial):
# Hyperparameters
lr = trial.suggest_loguniform("lr", 1e-5, 1e-2)
depth = trial.suggest_int("depth", 2, 8)
# Fake expensive evaluation
loss = (depth * 0.1) + (np.log1p(1/lr) * 0.05) + np.random.normal(0, 0.02)
return loss
# Custom sampling strategy that ensembles surrogate predictions
class EnsembleSampler(optuna.samplers.BaseSampler):
def __init__(self):
self.surrogates = build_surrogates()
def infer_relative_search_space(self, study, trial):
return None # use independent sampling
def sample_relative(self, study, trial, search_space):
return {}
def sample_independent(self, study, trial, param_name, distribution):
trials = study.get_trials(deepcopy=False)
# Warm-up phase: random sampling
if len(trials) < 15:
return optuna.samplers.RandomSampler().sample_independent(
study, trial, param_name, distribution
)
# Collect training data
X = []
y = []
for t in trials:
if t.values:
X.append([t.params["lr"], t.params["depth"]])
y.append(t.values[0])
X = np.array(X)
y = np.array(y)
train_surrogates(self.surrogates, X, y)
# Generate candidate points
candidates = np.random.uniform(
low=distribution.low, high=distribution.high, size=64
)
# Predict surrogate losses
if param_name == "lr":
Xcand = np.column_stack([candidates, np.full_like(candidates, trial.params.get("depth", 5))])
else:
Xcand = np.column_stack([np.full_like(candidates, trial.params.get("lr", 1e-3)), candidates])
preds = ensemble_predict(self.surrogates, Xcand)
# Pick best predicted candidate
return float(candidates[np.argmin(preds)])
# Run ensemble-driven BO
study = optuna.create_study(sampler=EnsembleSampler(), direction="minimize")
study.optimize(objective, n_trials=40)
print("Best:", study.best_params)總結
直接調用現成的庫往往難以解決複雜的工業級問題。上述這十個技巧,本質上都是在彌合理論假設(如平滑性、無限算力、同質噪聲)與工程現實(如預算限制、離散參數、失敗試驗)之間的鴻溝。
在實際應用中,不要把貝葉斯優化當作一個不可干預的黑盒。它應該是一個可以深度定製的組件。只有當你根據具體問題的特性,去精心設計搜索空間、調整採集策略並引入必要的約束時,貝葉斯優化才能真正成為提升模型性能的加速器,而不是消耗 GPU 資源的無底洞。
https://avoid.overfit.cn/post/bb15da0bacca46c4b0f6a858827b242f