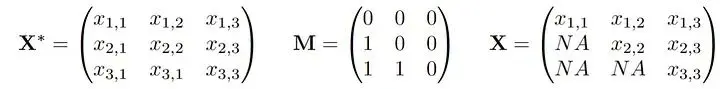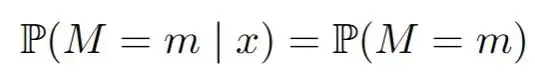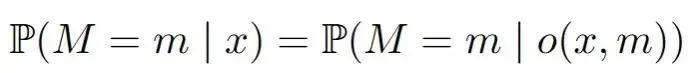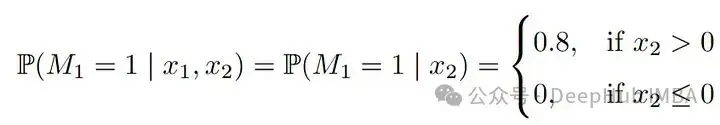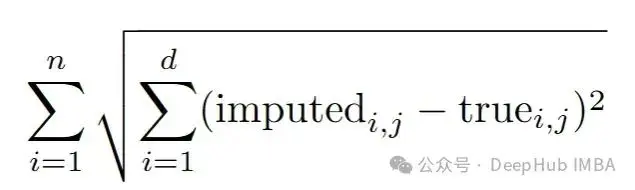本文將探討了缺失值插補的不同方法,並比較了它們在復原數據真實分佈方面的效果,處理插補是一個不確定性的問題,尤其是在樣本量較小或數據複雜性高時的挑戰,應選擇能夠適應數據分佈變化並準確插補缺失值的方法。
我們假設存在一個潛在的分佈P,從中得出觀察值X。此外,還繪製了一個與X相同維數的0/1向量,我們稱這個向量為M,實際觀測到的數據向量X被M掩碼為X。我們觀測到聯合向量(X,M)的n個獨立同分布(i.i.d)副本。如果我們把它寫成一個數據矩陣,它可能看起來像這樣:
較小的x,m表示“觀察到的”,而較大的值則表示隨機數量。大家討論的缺失機制就是對(X*,M)的關係或聯合分佈的假設:
完全隨機缺失(MCAR):一個值丟失的概率就像拋硬幣一樣,與數據集中的任何變量無關。缺失值只是一件麻煩事。你可以忽略它們,只關注數據集中完全觀察到的部分,這樣就不會有偏差。在數學中,對於所有m和x:
隨機缺失(MAR):缺失的概率現在可以依賴於數據集中觀察到的變量。一個典型的例子是兩個變量,比如收入和年齡,其中年齡總是被觀察到,但收入可能會因為年齡的某些值而丟失。這可能聽起來很合理,但這裏可能會變得複雜。在數學中,對於所有m和x:
非隨機缺失(MNAR):這裏一切皆有可能,我們不能籠統地概括。但是最終我們需要學習給定一個模式m '中觀測值的缺失值的條件分佈,以便在另一個模式m中推算。
實現這一點的著名的方法稱為鏈式方程多重插補(Multiple Imputation by Chained Equations, MICE):首先使用簡單的插補方法填充值,例如均值插補。然後對於每一次迭代t,對每一個變量j,根據所有其他已插補的變量進行迴歸分析(這些變量已被插補)。然後將這些變量的值填入已學習的插補器中,用於所有未觀察到的X_j。在R語言中,可以方便地使用mice包來實現。我這種方法在實際應用中效果非常好,MICE中重現某些實例的底層分佈的能力非常驚人。我們下面會用一個非常簡單的例子(只有一個變量缺失,因此我們可以手動編碼),模擬MICE通常會迭代執行的過程,以更好地瞭解他的工作原理。
數據
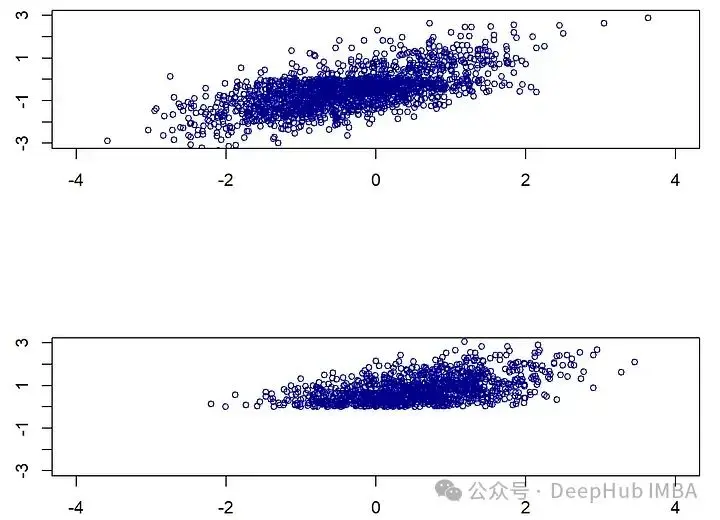
我們將看一個非常簡單但具有説明性的例子:考慮一個具有兩個聯合正態變量X_1, X_2的數據集。我們假設兩個變量的方差為1,正相關係數為0.5。為了方便説明,我們假設X_1是收入的對數,X_2是年齡。另外我們設置收入X_1存在缺失機制,即當年齡“高”時,X_1往往會缺失。這就是我們設的:
當X_2(年齡)較大(即大於0)時,X_1(收入)缺失的概率為0.8。由於我們假設X_2總是被觀察到,這是一個教科書式的MAR示例,它有兩種模式,一種是所有變量都被完全觀察到(m1),另一種是(m2),其中X_1缺失。儘管這個例子很簡單,但如果我們假設年齡越大,收入越高,那麼從一種模式轉換到另一種模式時,收入和年齡的分佈就會發生明顯的變化。在模式m2中,收入缺失,觀察到的年齡和(未觀察到的)收入的值都趨向於更高。
我們先看一下生成數據的代碼:
library(MASS)
library(mice)
set.seed(10)
n<-3000
Xstar<-mvrnorm(n=n, mu=c(0,0), Sigma=matrix( c(1,0.7,0.7,1), nrow=2, byrow=T ))
colnames(Xstar) <-paste0("X",1:2)
## Introduce missing mechanisms
M<-matrix(0, ncol=ncol(Xstar), nrow=nrow(Xstar))
M[Xstar[,2] >0, 1]<-sample(c(0,1), size=sum(Xstar[,2] >0), replace=T, prob=c(1-0.8,0.8) )
## This gives rise to the observed dataset by masking X^* with M:
X<-Xstar
X[M==1] <-NA
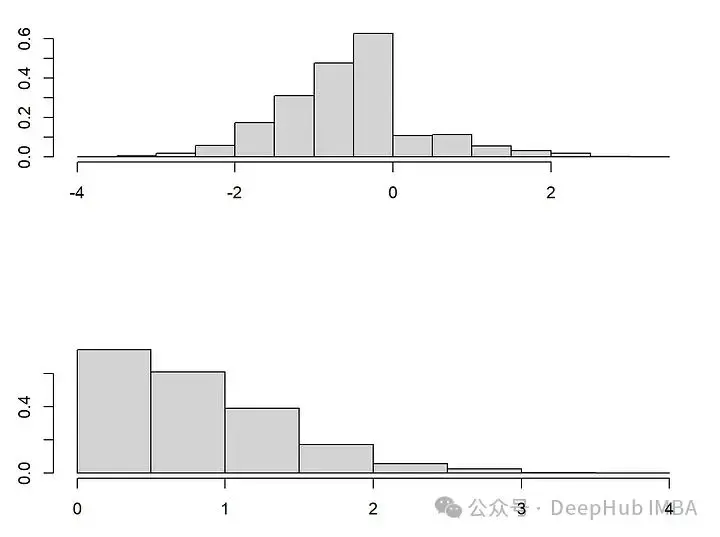
## Plot the distribution shift
par(mfrow=c(2,1))
plot(Xstar[!is.na(X[,1]),1:2], xlab="", main="", ylab="", cex=0.8, col="darkblue", xlim=c(-4,4), ylim=c(-3,3))
plot(Xstar[is.na(X[,1]),1:2], xlab="", main="", ylab="", cex=0.8, col="darkblue", xlim=c(-4,4), ylim=c(-3,3))插補是一個分佈預測問題
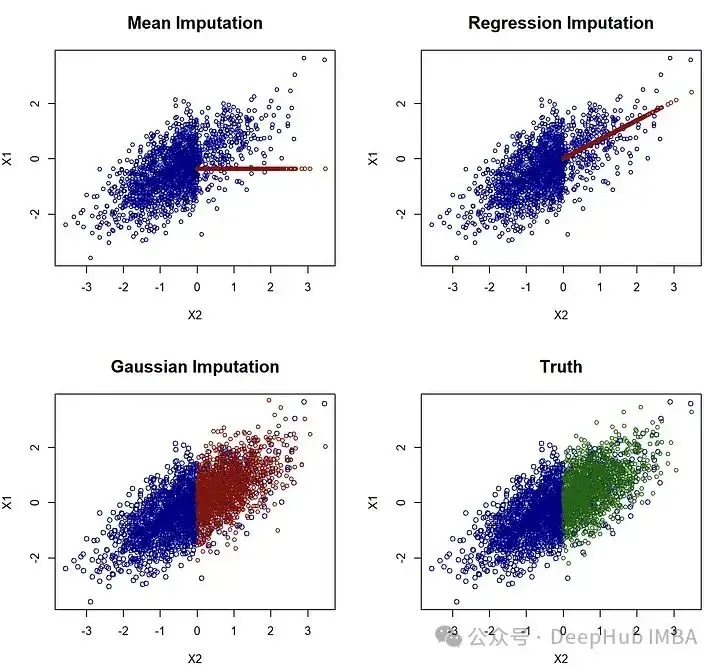
(通用的)插補的目標應該是儘可能地複製底層數據分佈。為了説明這一點,考慮第一個例子,其中p=0,這樣只有X_1缺失值現在將嘗試使用著名的MICE方法來插補這個例子。由於只有X_1缺失,可以手動實現這一點。我們從均值插補開始,簡單地計算在觀測到的模式中X_1的均值,並將這個均值填補到NA的位置。我們還使用了更為複雜的迴歸插補:在觀測到X_1的模式中,將X_1對X_2進行迴歸分析,然後對每個缺失的X_1觀測值,我們插入迴歸的預測值。最後,對於高斯插補,我們從X_1對X_2的同樣迴歸開始,但隨後通過從高斯分佈中抽取來插補每個缺失的X_1值。也就是説我們不是僅插補條件期望(即條件分佈的中心),而是從這個分佈中抽取。這導致了一種隨機插補,起初可能有些違反直覺,但實際上會帶來最好的結果:
## (0) Mean Imputation: This would correspond to "mean" in the mice R package ##
# 1. Estimate the mean
meanX<-mean(X[!is.na(X[,1]),1])
## 2. Impute
meanimp<-X
meanimp[is.na(X[,1]),1] <-meanX
## (1) Regression Imputation: This would correspond to "norm.predict" in the mice R package ##
# 1. Estimate Regression
lmodelX1X2<-lm(X1~X2, data=as.data.frame(X[!is.na(X[,1]),]) )
## 2. Impute
impnormpredict<-X
impnormpredict[is.na(X[,1]),1] <-predict(lmodelX1X2, newdata=as.data.frame(X[is.na(X[,1]),]) )
## (2) Gaussian Imputation: This would correspond to "norm.nob" in the mice R package ##
# 1. Estimate Regression
#lmodelX1X2<-lm(X1~X2, X=as.data.frame(X[!is.na(X[,1]),]) )
# (same as before)
## 2. Impute
impnorm<-X
meanx<-predict(lmodelX1X2, newdata=as.data.frame(X[is.na(X[,1]),]) )
var<-var(lmodelX1X2$residuals)
impnorm[is.na(X[,1]),1] <-rnorm(n=length(meanx), mean=meanx, sd=sqrt(var) )
## Plot the different imputations
par(mfrow=c(2,2))
plot(meanimp[!is.na(X[,1]),c("X2","X1")], main=paste("Mean Imputation"), cex=0.8, col="darkblue", cex.main=1.5)
points(meanimp[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
plot(impnormpredict[!is.na(X[,1]),c("X2","X1")], main=paste("Regression Imputation"), cex=0.8, col="darkblue", cex.main=1.5)
points(impnormpredict[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation"), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
#plot(Xstar[,c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
plot(Xstar[!is.na(X[,1]),c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
points(Xstar[is.na(X[,1]),c("X2","X1")], col="darkgreen", cex=0.8 )研究這張圖可以立即發現,均值和迴歸插補並不好,因為它們完全未能重現原始數據分佈。相比之下,高斯插補看起來相當不錯,事實上,我認為很難將其與真實情況區分開來。這可能看起來只是一個技術概念,但這有其後果。想象一下,如果你得到了任何這些插補的數據集,現在你想要找到在將X_2對X_1進行迴歸時的迴歸係數(與我們用於插補的操作相反)。在這種情況下,真實值由beta=cov(X_1, X_2)/var(X_1)=0.7給出。
## Regressing X_2 onto X_1
## mean imputation estimate
lm(X2~X1, data=data.frame(meanimp))$coefficients["X1"]
## beta= 0.61
## regression imputation estimate
round(lm(X2~X1, data=data.frame(impnormpredict))$coefficients["X1"],2)
## beta= 0.90
## Gaussian imputation estimate
round(lm(X2~X1, data=data.frame(impnorm))$coefficients["X1"],2)
## beta= 0.71
## Truth imputation estimate
round(lm(X2~X1, data=data.frame(Xstar))$coefficients["X1"],2)
## beta= 0.71高斯插補的結果非常接近0.7(0.71),更重要的是,它非常接近使用完整(未觀測)數據得到的估計!而均值插補低估了beta值,迴歸插補則高估了beta值。迴歸插補因為條件均值插補人為地增強了變量之間的關係,這將導致在科學和(數據科學)實踐中估計出的效應被過高估計!
迴歸插補可能看起來過於簡單,但是在機器學習和其他領域中非常常用的插補方法正是這樣工作的。例如,knn插補和隨機森林插補(即missForest)。特別是隨機森林插補在幾篇基準測試論文中受到讚揚和推薦,且應用非常廣泛。missForest是在觀測數據上擬合一個隨機森林,然後簡單地通過條件均值進行插補,使用它的結果將與迴歸插補非常相似,從而導致變量之間關係的人為強化和估計的偏差!
如何評估插補方法?
上面我們已經説了應將插補視為一個分佈預測的問題,那麼這個分佈預測的問題應該如何評估呢?
設想我們開發了一種新的插補方法,現在想要與已存在的方法如missForest、MICE或GAIN進行基準測試。這種情況下,我們人為地引入缺失值。然後將這個真實數據集與我們的插補結果進行比較。我們假設上面的迴歸插補是一種新方法,我們想要將其與均值和高斯插補進行比較。
即使在最有聲望的會議中,也是通過計算均方根誤差(RMSE)來完成的:
但是使用RMSE來評估我們的插補將偏向於那些插補條件均值的方法,如迴歸插補、knn插補和missForest。
而就像我們要説明的問題,由於插補本質上是一個分佈預測問題,因此除了使用RMSE等統計指標之外,還應評估插補方法是否能夠恢復數據的整體分佈。這可以通過比較不同插補方法生成的數據分佈的統計特性(如均值、方差、偏度等)或使用更復雜的分佈相似性度量(如地球移動者距離或Kullback-Leibler散度)來實現。這裏使用使用能量距離來衡量完全觀測數據的分佈與插補“分佈”之間的差異
能量距離:能量距離是一種度量兩個分佈之間差異的統計量,它基於從兩個分佈中隨機抽取樣本對的距離。在插補的上下文中,它能有效地評估插補數據分佈與原始數據分佈之間的相似性。
通過使用能量距離等分佈敏感的評估指標,我們可以更準確地評估插補方法是否能夠恢復數據的原始統計特性,而不僅僅是平均水平上的接近性。這種方法特別適合於評估那些旨在捕捉數據複雜依賴性和分佈特徵的高級插補技術。
library(energy)
## Function to calculate the energy distance:
# impX is the imputed data set
# Xstar is the fully observed data set
## Calculating the energy distance using the eqdist.e function of the energy package
energycalc<-function(impX, Xstar){
# Note: eqdist.e calculates the energy statistics for a test, which is actually
# = n^2/(2n)*energydistance(impX,Xstar), but we we are only interested in relative values
round(eqdist.e( rbind(Xstar,impX), c(nrow(Xstar), nrow(impX)) ),2)
}現在我們將這兩個分數應用到這個研究項目中,並測試我們的迴歸imputation是否比其他兩個更好:
par(mfrow=c(2,2))
## Same plots as before, but now with RMSE and energy distance
## added
plot(meanimp[!is.na(X[,1]),c("X2","X1")], main=paste("Mean Imputation", "\nRMSE", RMSEcalc(meanimp, Xstar), "\nEnergy", energycalc(meanimp, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(meanimp[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
plot(impnormpredict[!is.na(X[,1]),c("X2","X1")], main=paste("Regression Imputation","\nRMSE", RMSEcalc(impnormpredict, Xstar), "\nEnergy", energycalc(impnormpredict, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impnormpredict[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation","\nRMSE", RMSEcalc(impnorm, Xstar), "\nEnergy", energycalc(impnorm, Xstar)), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
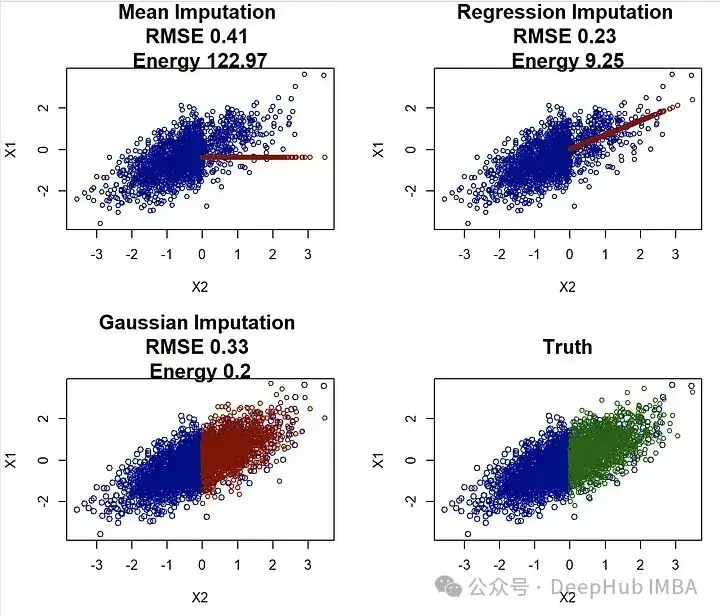
plot(Xstar[!is.na(X[,1]),c("X2","X1")], main="Truth", col="darkblue", cex.main=1.5)
points(Xstar[is.na(X[,1]),c("X2","X1")], col="darkgreen", cex=0.8 )在使用均方根誤差(RMSE)評估時,迴歸插補看起來表現非常好!它超過了均值插補和高斯插補。但是這與我們上面的分析相沖突,選擇迴歸插補可能會導致高度偏見的結果。而(標度化的)能量距離正確地識別出高斯插補是最佳方法,這與視覺和更好的參數估計相一致。
所以,當評估插補方法時(當真實數據可用時),應避免使用像RMSE和MAE這樣的度量。而應該被視為並作為分佈預測問題來評估,應使用諸如能量距離之類的分佈度量。將RMSE作為評估工具的過度使用對這一領域的研究有一些嚴重的影響。
當底層觀察數據不可用時,評估問題變得更加困難。這篇論文[1]中,開發了一個分數,即使在這種情況下也能對插補方法進行排名!
library(mice)
source("Iscore.R")
methods<-c("mean", #mice-mean
"norm.predict", #mice-sample
"norm.nob") # Gaussian Imputation
## We first define functions that allow for imputation of the three methods:
imputationfuncs<-list()
imputationfuncs[["mean"]] <-function(X,m){
# 1. Estimate the mean
meanX<-mean(X[!is.na(X[,1]),1])
## 2. Impute
meanimp<-X
meanimp[is.na(X[,1]),1] <-meanX
res<-list()
for (lin1:m){
res[[l]] <-meanimp
}
return(res)
}
imputationfuncs[["norm.predict"]] <-function(X,m){
# 1. Estimate Regression
lmodelX1X2<-lm(X1~., data=as.data.frame(X[!is.na(X[,1]),]) )
## 2. Impute
impnormpredict<-X
impnormpredict[is.na(X[,1]),1] <-predict(lmodelX1X2, newdata=as.data.frame(X[is.na(X[,1]),]) )
res<-list()
for (lin1:m){
res[[l]] <-impnormpredict
}
return(res)
}
imputationfuncs[["norm.nob"]] <-function(X,m){
# 1. Estimate Regression
lmodelX1X2<-lm(X1~., data=as.data.frame(X[!is.na(X[,1]),]) )
## 2. Impute
impnorm<-X
meanx<-predict(lmodelX1X2, newdata=as.data.frame(X[is.na(X[,1]),]) )
var<-var(lmodelX1X2$residuals)
res<-list()
for (lin1:m){
impnorm[is.na(X[,1]),1] <-rnorm(n=length(meanx), mean=meanx, sd=sqrt(var) )
res[[l]] <-impnorm
}
return(res)
}
scoreslist<-Iscores_new(X,imputations=NULL, imputationfuncs=imputationfuncs, N=30)
scores<-do.call(cbind,lapply(scoreslist, function(x) x$score ))
names(scores)<-methods
scores[order(scores)]
# mean norm.predict norm.nob
# -0.7455304 -0.5702136 -0.4220387 無需看到缺失數據的值,分數也能夠識別分佈,特別是當數據有兩個以上的維度時。
隨機缺失比你想象的更奇怪
當閲讀關於缺失值插補的文獻時,人們容易認為在缺失數據機製為MAR(Missing At Random,隨機缺失)的情況下問題已經解決,而所有的缺失問題都來自於是否可以假設為MAR。雖然在使用最大似然等標準程序時這可能是正確的,但如果想要找到一個好的(非參數的)插補方法,情況並非如此。
論文[1]討論了在MAR下可能發生的複雜分佈變化,當從完全觀測的模式變化到一個想要插補的模式時,在觀測變量中是否可能發生的分佈變化呢?回到上面的例子,其中將X_1設為收入,將X_2設為年齡。在第一幅圖中就能看到的,分佈看起來相當不同。而條件分佈 X_1 | X_2 保持不變!這在原則上允許識別正確的插補分佈。
這一發現對於理解和處理MAR下的缺失數據具有重要意義。儘管數據可能看起來在全面觀測和部分缺失時有不同的分佈,通過關注條件分佈的穩定性,可以更精確地插補缺失值。也就是説非參數插補技術能夠適應數據的這種內在複雜性,而不僅僅是簡單地應用參數方法或假設數據具有均勻分佈。在實際應用中,這種深入分析揭示了為何簡單的插補方法(如均值插補或條件均值插補)可能不足以捕捉數據的真實結構,尤其是在涉及複雜關聯和動態分佈時。
library(drf)
## mice-DRF ##
par(mfrow=c(2,2))
#Fit DRF
DRF<-drf(X=X[!is.na(X[,1]),2, drop=F], Y=X[!is.na(X[,1]),1, drop=F], num.trees=100)
impDRF<-X
# Predict weights for unobserved points
wx<-predict(DRF, newdata=X[is.na(X[,1]),2, drop=F] )$weights
impDRF[is.na(X[,1]),1] <-apply(wx,1,function(wxi) sample(X[!is.na(X[,1]),1, drop=F], size=1, replace=T, prob=wxi))
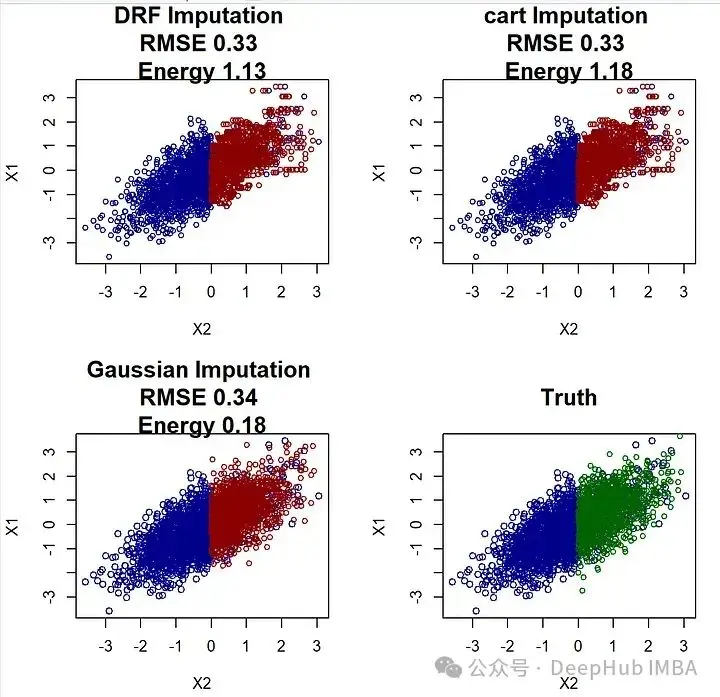
plot(impDRF[!is.na(X[,1]),c("X2","X1")], main=paste("DRF Imputation", "\nRMSE", RMSEcalc(impDRF, Xstar), "\nEnergy", energycalc(impDRF, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impDRF[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
## mice-cart##
impcart<-X
impcart[is.na(X[,1]),1] <-mice.impute.cart(X[,1], ry=!is.na(X[,1]), X[,2, drop=F], wy=NULL)
plot(impDRF[!is.na(X[,1]),c("X2","X1")], main=paste("cart Imputation", "\nRMSE", RMSEcalc(impcart, Xstar), "\nEnergy", energycalc(impcart, Xstar)), cex=0.8, col="darkblue", cex.main=1.5)
points(impDRF[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )
plot(impnorm[!is.na(X[,1]),c("X2","X1")], main=paste("Gaussian Imputation","\nRMSE", RMSEcalc(impnorm, Xstar), "\nEnergy", energycalc(impnorm, Xstar)), col="darkblue", cex.main=1.5)
points(impnorm[is.na(X[,1]),c("X2","X1")], col="darkred", cex=0.8 )雖然mice-cart和mice-DRF都做得不錯,但它們仍然不如高斯插補那麼好。這本身並不令人驚訝,因為在這種情況下,高斯插補是理想的插補方法(因為 (X_1, X_2) 確實是高斯分佈的)。而X_2中的分佈變化可能可能導致mice-cart和mice-DRF在恢復3000個觀測值的分佈時遇到困難(這些方法通常非常有效)。
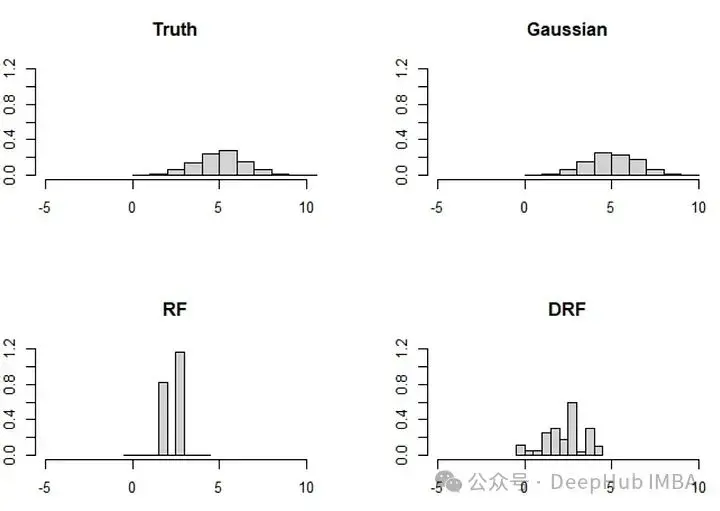
論文還討論了一個類似的,但更極端的例子,涉及兩個變量(X_1, X_2)。在這個例子中,分佈變化更為顯著,基於森林的方法相應地面臨挑戰:
分佈變化的影響:當底層數據的分佈發生顯著變化時,基於模型的插補方法(如基於決策樹或隨機森林的方法)可能難以準確地恢復數據的真實分佈。這是因為這些模型依賴於數據中存在的模式和結構,而當這些模式和結構因為缺失數據而改變時,模型的效果可能會下降。
高斯插補的適用性:高斯插補假設數據遵循高斯分佈,這使得它在處理本質上呈高斯分佈的數據時非常有效。對於這種類型的數據,高斯插補能夠更好地捕捉數據的整體統計特性,包括均值和協方差結構。
方法選擇的重要性:選擇正確的插補方法對於確保插補結果的質量至關重要。在面對複雜的數據和分佈時,理解每種方法的優勢和侷限性可以幫助研究人員和實踐者選擇最適合他們數據特徵的插補方法。
總結
缺失值確實是一個棘手的問題。,處理缺失值的最佳方式是儘量避免它們的出現,但是這幾乎是不可能的,所以即使只考慮隨機缺失(MAR),尋找插補方法的工作還遠未結束。我們仍然缺乏一種能夠(1)進行非參數分佈預測和(2)適應在MAR下可能發生的分佈變化的方法。有時也感覺人們將問題複雜化了,因為一些MICE方法表現得非常出色,可能已經足以解決許多缺失值問題。
有一些非常先進的機器學習方法,如GAIN及其變體,試圖使用神經網絡來插補數據。方法可能是正確的,因為它們遵循了正確的思路:插補在觀察到的情況下缺失的條件分佈。但是使用它們一段時間後,性能並不能讓人滿意,尤其是與MICE相比。
所以如果我遇到一個缺失值問題,可以首先嚐試的是mice-cart或在論文中開發的新方法mice-DRF。它們重現數據的能力非常驚人。但是這些方法需要至少一箇中等的樣本大小,例如超過200或300。如果在少於200個觀察的情況下,可以選擇更簡單的方法,如高斯插補。如果你想從這些方法中找到最好的,可以嘗試使用論文中的評分規則來找到最好的方法。
最後別忘了這些方法都無法有效地處理插補不確定性!因為我們在這篇文章中只討論了單一插補。正確的多重插補將需要考慮插補方法本身的不確定性,這通常使用貝葉斯方法完成,這可能又是一篇論文了。
最後:因為原論文都是使用R進行編寫,我又對R不太熟悉,自己使用進行Python復現有幾段出現了問題,所以就直接貼R的代碼了,有興趣的小夥伴請自行使用 Python重寫。另外,GPT4的改寫效果也不好,而copilot則直接提示無法改寫,所以如果你有成功的的GPT4改寫的Prompt也可以聯繫我,感謝。
最後本文引用的論文:
What Is a Good Imputation Under MAR Missingness? [1]
https://avoid.overfit.cn/post/9f66c5f8cd204ed685af0744b935ddd5
作者: Jeffrey Näf