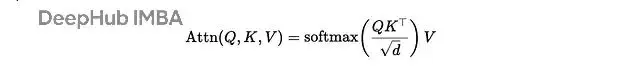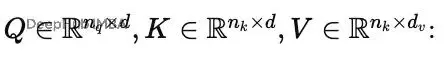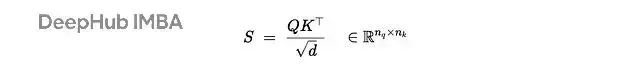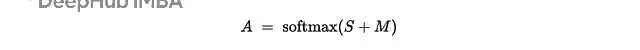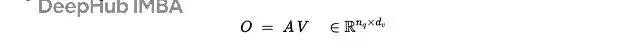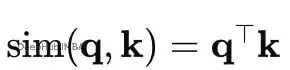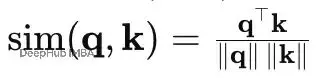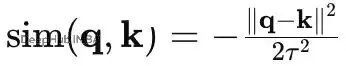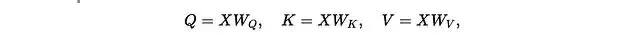注意力機制聽起來很玄乎,但我們可以把它看作一個軟k-NN算法。查詢向量問:"誰跟我最像?",softmax投票,相似的鄰居們返回一個加權平均值。這就是注意力頭的另外一種解釋: 一個可微分的軟k-NN:計算相似度 → softmax轉換為權重 → 對鄰居值求加權平均。
通過
1/sqrt(d)縮放防止softmax在高維時飽和,掩碼決定哪些位置可以互相"看見"(處理因果關係、填充等問題)。
想象有個查詢向量 𝐪 在問:"哪些token跟我相似?"
接下來就是三步走:
- 把 𝐪 跟每個鍵 𝒌 ᵢ 做比較,算出相似度分數
- Softmax把這些分數歸一化成概率分佈(分數越高權重越大)
- 用這些權重對值向量 𝐯ᵢ 做加權平均
這就是注意力的另外一種解釋:考慮序列順序的軟鄰居平均算法。
數學推導
單注意力頭,鍵/查詢維度是 𝒅,值維度是 𝒅 ᵥ:
相似度計算用縮放點積:
可選的掩碼操作:
按行做softmax得到權重:
最後計算值的加權平均:
為什麼要除以 sqrt(d)?
隨機d維向量的點積會按 O(sqrt(d)) 增長。不做縮放的話,softmax就變成了勝者通吃(一個權重接近1,其他都接近0),梯度直接就消失了,所以除以sqrt(d)能讓分數方差保持在合理範圍,這樣softmax的熵也就穩定了。
掩碼的作用
掩碼 𝐌 在softmax之前加入:
因果掩碼用於語言建模,阻止位置 t 看到 j > t 的未來信息。填充掩碼則屏蔽那些佔位符token。數學上就是 A=softmax(S+M),其中 Mᵢⱼ=0 表示允許,-∞ 表示阻塞。
軟k-NN的不同變體
換個相似度函數就是換個歸納偏置:
點積考慮方向和幅度:
餘弦相似度只看角度,忽略長度:
負距離(RBF風格)專注歐幾里得鄰域:
之後都是 softmax → 權重 → 加權平均。温度參數τ控制軟硬程度:τ越小越尖鋭,越像argmax。
NumPy最小實現
目標很簡單:清晰勝過速度。
import numpy as np
def softmax(x, axis=-1):
x = x - np.max(x, axis=axis, keepdims=True) # numerical stability
ex = np.exp(x)
return ex / np.sum(ex, axis=axis, keepdims=True)
def attention(Q, K, V, mask=None):
"""
Q: (n_q, d), K: (n_k, d), V: (n_k, d_v)
mask: (n_q, n_k) with 0=keep, -inf=block (or None)
Returns: (n_q, d_v), (n_q, n_k)
"""
d = Q.shape[-1]
scores = (Q @ K.T) / np.sqrt(d) # (n_q, n_k)
if mask is not None:
scores = scores + mask
weights = softmax(scores, axis=-1) # (n_q, n_k)
return weights @ V, weights簡單實驗:6個二維token
創建6個token embedding和一個查詢,看看權重分配:
# toy data
np.random.seed(7)
n_tokens, d, d_v = 6, 2, 2
K = np.array([[ 1.0, 0.2],
[ 0.9, 0.1],
[ 0.2, 1.0],
[-0.2, 0.9],
[ 0.0, -1.0],
[-1.0, -0.6]])
# Values as a simple linear map of keys (for intuition)
Wv = np.array([[0.7, 0.1],
[0.2, 0.9]])
V = K @ Wv
# Query near the first cluster
Q = np.array([[0.8, 0.15]]) # (1, d)
out, W = attention(Q, K, V)
print("Attention weights:", np.round(W, 3))
print("Output vector:", np.round(out, 3))
# -> weights ~ heavier on the first two neighbors
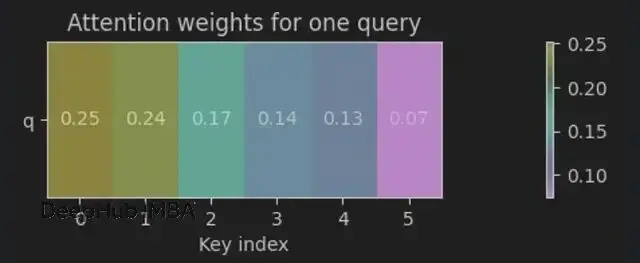
Attention weights: [[0.252 0.236 0.174 0.138 0.126 0.075]]
Output vector: [[0.318 0.221]]權重可視化:
查詢通過縮放點積+softmax給鍵分配概率(權重和為1),大部分權重落在最近的鄰居上(0≈0.25,1≈0.24),輸出就是這些值的加權平均。所以可以説注意力就是軟k-NN。
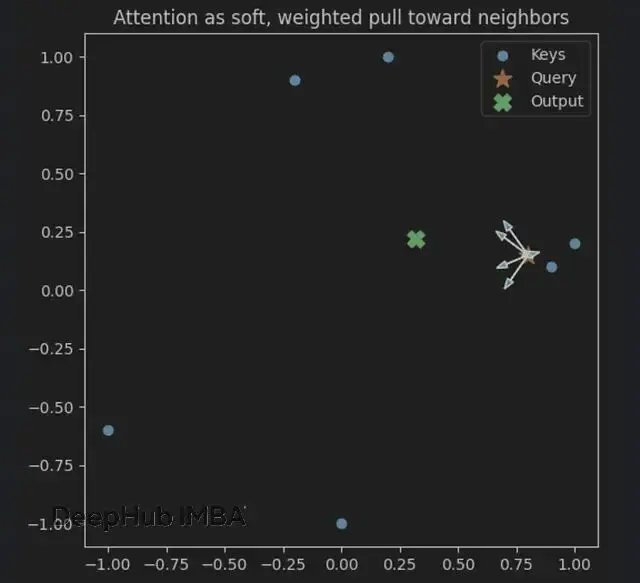
使用幾何視角更直觀:
查詢(★)感受到來自附近鍵(●)的加權拉力,箭頭長度正比於注意力權重。輸出(✖)就是鄰居們的加權重心。
三種相似度的對比
試試不同的相似度函數:
def attention_with_sim(Q, K, V, sim="dot", tau=1.0, eps=1e-9):
if sim == "dot":
scores = (Q @ K.T) / np.sqrt(K.shape[-1])
elif sim == "cos":
Qn = Q / (np.linalg.norm(Q, axis=-1, keepdims=True) + eps)
Kn = K / (np.linalg.norm(K, axis=-1, keepdims=True) + eps)
scores = (Qn @ Kn.T) / tau
elif sim == "rbf":
# scores = -||q-k||^2 / (2*tau^2)
q2 = np.sum(Q**2, axis=-1, keepdims=True) # (n_q, 1)
k2 = np.sum(K**2, axis=-1, keepdims=True).T # (1, n_k)
qk = Q @ K.T # (n_q, n_k)
d2 = q2 + k2 - 2*qk
scores = -d2 / (2 * tau**2)
else:
raise ValueError("sim in {dot, cos, rbf}")
W = softmax(scores, axis=-1)
return W @ V, W, scores
for sim in ["dot", "cos", "rbf"]:
out_s, W_s, _ = attention_with_sim(Q, K, V, sim=sim, tau=0.5)
print(sim, "weights:", np.round(W_s, 3), "out:", np.round(out_s, 3))
[#結果](#結果)
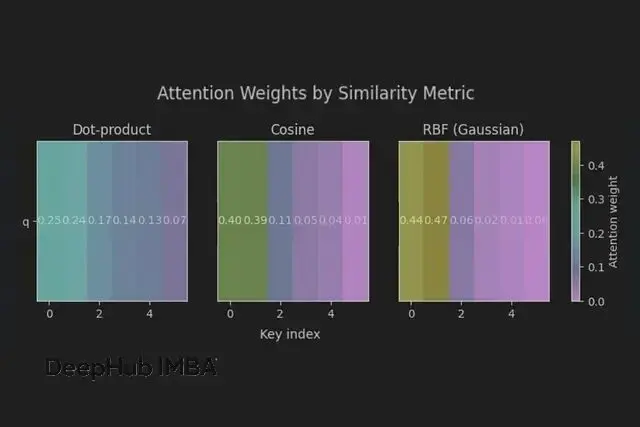
dot weights: [[0.252 0.236 0.174 0.138 0.126 0.075]] out: [[0.318 0.221]]
cos weights: [[0.397 0.394 0.113 0.05 0.037 0.008]] out: [[0.576 0.287]]
rbf weights: [[0.443 0.471 0.055 0.021 0.01 0. ]] out: [[0.651 0.268]]相似度選擇就是歸納偏置選擇。餘弦看角度,RBF看距離,點積兩者兼顧。
同一個查詢,三種視角。餘弦和RBF在最近鍵上更加聚焦,點積分佈相對均勻。
因果掩碼和填充掩碼
語言建模裏經常用到:
因果掩碼防止模型偷看未來,位置 t 不能看到 > t 的內容。填充掩碼忽略那些沒有實際內容的佔位符。
# Causal mask for sequence length n (upper-triangular blocked)
n = 6
mask = np.triu(np.ones((n, n)) * -1e9, k=1)
# Visualize structure by setting Q=K=V (toy embeddings)
X = K
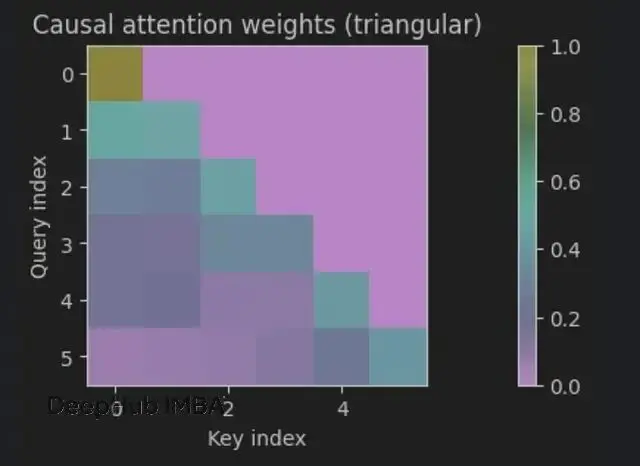
out_seq, A = attention(X, X, X, mask=mask)
# Row sums stay 1.0 (softmax is row-wise):
print(np.allclose(np.sum(A, axis=1), 1.0))
[#True](#True)嚴格的下三角結構 —— 每個位置只能看到自己和過去的信息。
填充掩碼就簡單了:構建布爾掩碼,填充位置設為-∞,複用同一個attention函數即可。
縮放為什麼有效?
用隨機高維向量實驗一下:
def entropy(p, axis=-1, eps=1e-12):
p = np.clip(p, eps, 1.0)
return -np.sum(p * np.log(p), axis=axis)
nq = nk = 64
dims = [256*(2**i) for i in range(7)] # 256..16,384
trials = 5
H_max = np.log(nk)
for dim in dims:
H_u = []
H_s = []
for _ in range(trials):
Q = np.random.randn(nq, dim)
K = np.random.randn(nk, dim)
S_unscaled = Q @ K.T
S_scaled = S_unscaled / np.sqrt(dim)
H_u.append(entropy(softmax(S_unscaled, axis=-1), axis=-1).mean())
H_s.append(entropy(softmax(S_scaled, axis=-1), axis=-1).mean())
print(f"{dim:>6} | unscaled: {np.mean(H_u):.3f} scaled: {np.mean(H_s):.3f} (max={H_max:.3f})")
[#結果](#結果)
256 | unscaled: 0.280 scaled: 3.686 (max=4.159)
512 | unscaled: 0.165 scaled: 3.672 (max=4.159)
1024 | unscaled: 0.124 scaled: 3.682 (max=4.159)
2048 | unscaled: 0.078 scaled: 3.669 (max=4.159)
4096 | unscaled: 0.063 scaled: 3.689 (max=4.159)
8192 | unscaled: 0.041 scaled: 3.685 (max=4.159)
16384 | unscaled: 0.024 scaled: 3.694 (max=4.159)可以看到,縮放讓softmax更加可靠。
數據很明顯:未縮放時熵只有0.07-0.28,縮放後保持在3.68附近。64個鍵的最大熵是ln(64)≈4.16。
不縮放→接近獨熱分佈:一個鍵可以霸佔所有權重,梯度消失。
縮放後→高熵,權重分散:多個鄰居都有貢獻,梯度健康。
原理很簡單:獨立同分布隨機向量的點積方差∝d。維度增長時logits變大,softmax飽和。除以sqrt(d)把logit方差歸一化到O(1),保持softmax"温度"恆定。
1/sqrt(d)維護了可訓練性和穩定性 —— 注意力保持軟k-NN特性,不會退化成硬argmax。
一些常見問題
相似度太平→輸出模糊。降低温度/提高縮放;訓練投影矩陣W_Q、W_K分離token。
某個token佔主導→過於自信,系統脆弱。調節温度、加attention dropout、增加多頭多樣性。
選錯度量→關注錯了重點。角度問題用餘弦;距離問題用RBF;需要考慮幅度用點積。
從基礎到Transformer
加上可學習的投影矩陣:
複製h個頭,拼接輸出再用W_O混合 ,所以還是軟鄰居平均,只是這是在多個學習子空間裏並行。
總結
注意力機制沒那麼神秘,可以把它想象成帶可學習投影的軟k-NN。查詢問"誰像我",softmax把相似度轉成分佈,輸出就是加權平均。
只不過它多了兩個關鍵調節器:
1/sqrt(d)縮放保持logits在O(1)範圍,維持熵的穩定性。實驗證明沒有它會飽和(近似argmax),有它就能保持健康的軟性。
掩碼控制信息流:因果掩碼防止偷看未來,填充掩碼忽略無效內容。
相似度選擇就是歸納偏置選擇:點積(幅度+方向)、餘弦(角度)、RBF(歐氏距離)。多頭就是在並行子空間裏跑這套邏輯然後混合結果。
所以如果你還不理解注意力,可以直接把它,注意力就是一個帶温控的概率鄰居平均算法。温度設對了(1/sqrt(d)),鄰域選對了(相似度+掩碼),剩下的就是工程實現了。
https://avoid.overfit.cn/post/036fe92cd30245fbb4d7ff97f5301c36
作者:Joseph Robinson, Ph.D.